Accelerating expansion of the universe
| Part of a series on |
| Physical cosmology |
|---|

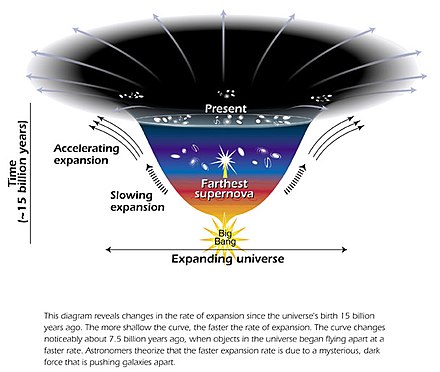
Observations show that the expansion of the universe is accelerating, such that the velocity at which a distant galaxy recedes from the observer is continuously increasing with time.[1][2][3] The accelerated expansion of the universe was discovered in 1998 by two independent projects, the Supernova Cosmology Project and the High-Z Supernova Search Team, which used distant type Ia supernovae to measure the acceleration.[4][5][6] The idea was that as type Ia supernovae have almost the same intrinsic brightness (a standard candle), and since objects that are farther away appear dimmer, the observed brightness of these supernovae can be used to measure the distance to them. The distance can then be compared to the supernovae's cosmological redshift, which measures how much the universe has expanded since the supernova occurred; the Hubble law established that the farther away that an object is, the faster it is receding. The unexpected result was that objects in the universe are moving away from one another at an accelerating rate. Cosmologists at the time expected that recession velocity would always be decelerating, due to the gravitational attraction of the matter in the universe. Three members of these two groups have subsequently been awarded Nobel Prizes for their discovery.[7] Confirmatory evidence has been found in baryon acoustic oscillations, and in analyses of the clustering of galaxies.
The accelerated expansion of the universe is thought to have begun since the universe entered its dark-energy-dominated era roughly 5 billion years ago.[8][notes 1] Within the framework of general relativity, an accelerated expansion can be accounted for by a positive value of the cosmological constant Λ, equivalent to the presence of a positive vacuum energy, dubbed "dark energy". While there are alternative possible explanations, the description assuming dark energy (positive Λ) is used in the current standard model of cosmology, which also includes cold dark matter (CDM) and is known as the Lambda-CDM model.
Background[edit]
−13 — – −12 — – −11 — – −10 — – −9 — – −8 — – −7 — – −6 — – −5 — – −4 — – −3 — – −2 — – −1 — – 0 — |
| |||||||||||||||||||||||||||||||||||||||
In the decades since the detection of cosmic microwave background (CMB) in 1965,[9] the Big Bang model has become the most accepted model explaining the evolution of our universe. The Friedmann equation defines how the energy in the universe drives its expansion.
where κ represents the curvature of the universe, a(t) is the scale factor, ρ is the total energy density of the universe, and H is the Hubble parameter.[10]
We define a critical density
and the density parameter
We can then rewrite the Hubble parameter as
where the four currently hypothesized contributors to the energy density of the universe are curvature, matter, radiation and dark energy.[11] Each of the components decreases with the expansion of the universe (increasing scale factor), except perhaps the dark energy term. It is the values of these cosmological parameters which physicists use to determine the acceleration of the universe.
The acceleration equation describes the evolution of the scale factor with time
where the pressure P is defined by the cosmological model chosen. (see explanatory models below)
Physicists at one time were so assured of the deceleration of the universe's expansion that they introduced a so-called deceleration parameter q0.[12] Current observations indicate this deceleration parameter is negative.
Relation to inflation[edit]
According to the theory of cosmic inflation, the very early universe underwent a period of very rapid, quasi-exponential expansion. While the time-scale for this period of expansion was far shorter than that of the current expansion, this was a period of accelerated expansion with some similarities to the current epoch.
Technical definition[edit]
The definition of "accelerating expansion" is that the second time derivative of the cosmic scale factor, , is positive, which is equivalent to the deceleration parameter, , being negative. However, note this does not imply that the Hubble parameter is increasing with time. Since the Hubble parameter is defined as , it follows from the definitions that the derivative of the Hubble parameter is given by
so the Hubble parameter is decreasing with time unless . Observations prefer , which implies that is positive but is negative. Essentially, this implies that the cosmic recession velocity of any one particular galaxy is increasing with time, but its velocity/distance ratio is still decreasing; thus different galaxies expanding across a sphere of fixed radius cross the sphere more slowly at later times.
It is seen from above that the case of "zero acceleration/deceleration" corresponds to is a linear function of , , , and .
Evidence for acceleration[edit]
The rate of expansion of the universe can be analyzed using the magnitude-redshift relationship of astronomical objects using standard candles, or their distance-redshift relationship using standard rulers. Also a factor is the growth of large-scale structure, finding that the observed values of the cosmological parameters are best described by models which include an accelerating expansion.
Supernova observation[edit]

In 1998, the first evidence for acceleration came from the observation of Type Ia supernovae, which are exploding white dwarf stars that have exceeded their stability limit. Because they all have similar masses, their intrinsic luminosity can be standardized. Repeated imaging of selected areas of the sky is used to discover the supernovae, then follow-up observations give their peak brightness, which is converted into a quantity known as luminosity distance (see distance measures in cosmology for details).[13] Spectral lines of their light can be used to determine their redshift.
For supernovae at redshift less than around 0.1, or light travel time less than 10 percent of the age of the universe, this gives a nearly linear distance–redshift relation due to Hubble's law. At larger distances, since the expansion rate of the universe has changed over time, the distance-redshift relation deviates from linearity, and this deviation depends on how the expansion rate has changed over time. The full calculation requires computer integration of the Friedmann equation, but a simple derivation can be given as follows: the redshift z directly gives the cosmic scale factor at the time the supernova exploded.
So a supernova with a measured redshift z = 0.5 implies the universe was 1/1 + 0.5 = 2/3 of its present size when the supernova exploded. In the case of accelerated expansion, is positive; therefore, was smaller in the past than today. Thus, an accelerating universe took a longer time to expand from 2/3 to 1 times its present size, compared to a non-accelerating universe with constant and the same present-day value of the Hubble constant. This results in a larger light-travel time, larger distance and fainter supernovae, which corresponds to the actual observations. Adam Riess et al. found that "the distances of the high-redshift SNe Ia were, on average, 10% to 15% farther than expected in a low mass density ΩM = 0.2 universe without a cosmological constant".[14] This means that the measured high-redshift distances were too large, compared to nearby ones, for a decelerating universe.[15]
Several researchers have questioned the majority opinion on the acceleration or the assumption of the "cosmological principle" (that the universe is homogeneous and isotropic).[16] For example, a 2019 paper analyzed the Joint Light-curve Analysis catalog of Type Ia supernovas, containing ten times as many supernova as were used in the 1998 analyses, and concluded that there was little evidence for a "monopole", that is, for an isotropic acceleration in all directions.[17][18] See also the section on Alternate theories below.
Baryon acoustic oscillations[edit]
In the early universe before recombination and decoupling took place, photons and matter existed in a primordial plasma. Points of higher density in the photon-baryon plasma would contract, being compressed by gravity until the pressure became too large and they expanded again.[12] This contraction and expansion created vibrations in the plasma analogous to sound waves. Since dark matter only interacts gravitationally, it stayed at the centre of the sound wave, the origin of the original overdensity. When decoupling occurred, approximately 380,000 years after the Big Bang,[19] photons separated from matter and were able to stream freely through the universe, creating the cosmic microwave background as we know it. This left shells of baryonic matter at a fixed radius from the overdensities of dark matter, a distance known as the sound horizon. As time passed and the universe expanded, it was at these inhomogeneities of matter density where galaxies started to form. So by looking at the distances at which galaxies at different redshifts tend to cluster, it is possible to determine a standard angular diameter distance and use that to compare to the distances predicted by different cosmological models.
Peaks have been found in the correlation function (the probability that two galaxies will be a certain distance apart) at 100 h−1 Mpc,[11] (where h is the dimensionless Hubble constant) indicating that this is the size of the sound horizon today, and by comparing this to the sound horizon at the time of decoupling (using the CMB), we can confirm the accelerated expansion of the universe.[20]
Clusters of galaxies[edit]
Measuring the mass functions of galaxy clusters, which describe the number density of the clusters above a threshold mass, also provides evidence for dark energy [further explanation needed].[21] By comparing these mass functions at high and low redshifts to those predicted by different cosmological models, values for w and Ωm are obtained which confirm a low matter density and a non-zero amount of dark energy.[15]
Age of the universe[edit]
Given a cosmological model with certain values of the cosmological density parameters, it is possible to integrate the Friedmann equations and derive the age of the universe.
By comparing this to actual measured values of the cosmological parameters, we can confirm the validity of a model which is accelerating now, and had a slower expansion in the past.[15]
Gravitational waves as standard sirens[edit]
Recent discoveries of gravitational waves through LIGO and VIRGO[22][23][24] not only confirmed Einstein's predictions but also opened a new window into the universe. These gravitational waves can work as sort of standard sirens to measure the expansion rate of the universe. Abbot et al. 2017 measured the Hubble constant value to be approximately 70 kilometres per second per megaparsec.[22] The amplitudes of the strain 'h' is dependent on the masses of the objects causing waves, distances from observation point and gravitational waves detection frequencies. The associated distance measures are dependent on the cosmological parameters like the Hubble Constant for nearby objects[22] and will be dependent on other cosmological parameters like the dark energy density, matter density, etc. for distant sources.[25][24]
Explanatory models[edit]
Dark energy[edit]
The most important property of dark energy is that it has negative pressure (repulsive action) which is distributed relatively homogeneously in space.
where c is the speed of light and ρ is the energy density. Different theories of dark energy suggest different values of w, with w < −1/3 for cosmic acceleration (this leads to a positive value of ä in the acceleration equation above).
The simplest explanation for dark energy is that it is a cosmological constant or vacuum energy; in this case w = −1. This leads to the Lambda-CDM model, which has generally been known as the Standard Model of Cosmology from 2003 through the present, since it is the simplest model in good agreement with a variety of recent observations. Riess et al. found that their results from supernova observations favoured expanding models with positive cosmological constant (Ωλ > 0) and a current accelerated expansion (q0 < 0).[14]
Phantom energy[edit]
Current observations allow the possibility of a cosmological model containing a dark energy component with equation of state w < −1. This phantom energy density would become infinite in finite time, causing such a huge gravitational repulsion that the universe would lose all structure and end in a Big Rip.[26] For example, for w = −3/2 and H0 =70 km·s−1·Mpc−1, the time remaining before the universe ends in this Big Rip is 22 billion years.[27]
Alternative theories[edit]
There are many alternative explanations for the accelerating universe. Some examples are quintessence, a proposed form of dark energy with a non-constant state equation, whose density decreases with time. A negative mass cosmology does not assume that the mass density of the universe is positive (as is done in supernova observations), and instead finds a negative cosmological constant. Occam's razor also suggests that this is the 'more parsimonious hypothesis'.[28][29] Dark fluid is an alternative explanation for accelerating expansion which attempts to unite dark matter and dark energy into a single framework.[30] Alternatively, some authors have argued that the accelerated expansion of the universe could be due to a repulsive gravitational interaction of antimatter[31][32][33] or a deviation of the gravitational laws from general relativity, such as massive gravity, meaning that gravitons themselves have mass.[34] The measurement of the speed of gravity with the gravitational wave event GW170817 ruled out many modified gravity theories as alternative explanations to dark energy.[35][36][37] Another type of model, the backreaction conjecture,[38][39] was proposed by cosmologist Syksy Räsänen:[40] the rate of expansion is not homogenous, but Earth is in a region where expansion is faster than the background. Inhomogeneities in the early universe cause the formation of walls and bubbles, where the inside of a bubble has less matter than on average. According to general relativity, space is less curved than on the walls, and thus appears to have more volume and a higher expansion rate. In the denser regions, the expansion is slowed by a higher gravitational attraction. Therefore, the inward collapse of the denser regions looks the same as an accelerating expansion of the bubbles, leading us to conclude that the universe is undergoing an accelerated expansion.[41] The benefit is that it does not require any new physics such as dark energy. Räsänen does not consider the model likely, but without any falsification, it must remain a possibility. It would require rather large density fluctuations (20%) to work.[40]
A final possibility is that dark energy is an illusion caused by some bias in measurements. For example, if we are located in an emptier-than-average region of space, the observed cosmic expansion rate could be mistaken for a variation in time, or acceleration.[42][43][44][45] A different approach uses a cosmological extension of the equivalence principle to show how space might appear to be expanding more rapidly in the voids surrounding our local cluster. While weak, such effects considered cumulatively over billions of years could become significant, creating the illusion of cosmic acceleration, and making it appear as if we live in a Hubble bubble.[46][47][48] Yet other possibilities are that the accelerated expansion of the universe is an illusion caused by the relative motion of us to the rest of the universe,[49][50] or that the supernova sample size used wasn't large enough.[51][52]
Theories for the consequences to the universe[edit]
As the universe expands, the density of radiation and ordinary dark matter declines more quickly than the density of dark energy (see equation of state) and, eventually, dark energy dominates. Specifically, when the scale of the universe doubles, the density of matter is reduced by a factor of 8, but the density of dark energy is nearly unchanged (it is exactly constant if the dark energy is the cosmological constant).[12]
In models where dark energy is the cosmological constant, the universe will expand exponentially with time in the far future, coming closer and closer to a de Sitter universe. This will eventually lead to all evidence for the Big Bang disappearing, as the cosmic microwave background is redshifted to lower intensities and longer wavelengths. Eventually, its frequency will be low enough that it will be absorbed by the interstellar medium, and so be screened from any observer within the galaxy. This will occur when the universe is less than 50 times its current age, leading to the end of cosmology as we know it as the distant universe turns dark.[53]
A constantly expanding universe with a non-zero cosmological constant has mass density decreasing over time. In such a scenario, the current understanding is that all matter will ionize and disintegrate into isolated stable particles such as electrons and neutrinos, with all complex structures dissipating away.[54] This scenario is known as "heat death of the universe" (also known as the Big Freeze).
Alternatives for the ultimate fate of the universe include the Big Rip mentioned above, a Big Bounce, or a Big Crunch.
See also[edit]
Notes[edit]
- ^ [8] Frieman, Turner & Huterer (2008) p. 6: "The Universe has gone through three distinct eras: radiation-dominated, z ≳ 3000; matter-dominated, 3000 ≳ z ≳ 0.5; and dark-energy-dominated, z ≲ 0.5. The evolution of the scale factor is controlled by the dominant energy form: a(t) ∝ t2/(3(1 + w)) (for constant w). During the radiation-dominated era, a(t) ∝ t1/2; during the matter-dominated era, a(t) ∝ t2/3; and for the dark energy-dominated era, assuming w = −1, asymptotically a(t) ∝ exp(Ht)."
p. 44: "Taken together, all the current data provide strong evidence for the existence of dark energy; they constrain the fraction of critical density contributed by dark energy, 0.76 ± 0.02, and the equation-of-state parameter, w ≈ −1 ± 0.1 (stat) ± 0.1 (sys), assuming that w is constant. This implies that the Universe began accelerating at redshift z ~ 0.4 and age t ~ 10 Gyr. These results are robust – data from any one method can be removed without compromising the constraints – and they are not substantially weakened by dropping the assumption of spatial flatness."
References[edit]
- ^ Overbye, Dennis (20 February 2017). "Cosmos Controversy: The Universe Is Expanding, but How Fast?". The New York Times. Retrieved 21 February 2017.
- ^ Scharping, Nathaniel (18 October 2017). "Gravitational Waves Show How Fast The Universe is Expanding". Astronomy. Retrieved 18 October 2017.
- ^ Weaver, Donna; Villard, Ray (11 March 2018). "Measuring universe expansion reveals mystery – Is something unpredicted going on in the depths of space?". Earth & Sky. Retrieved 11 March 2018.
- ^ "Nobel physics prize honours accelerating universe find". BBC News. 2011-10-04.
- ^ "The Nobel Prize in Physics 2011". Nobelprize.org. Retrieved 2011-10-06.
- ^ Peebles, P. J. E.; Ratra, Bharat (2003). "The cosmological constant and dark energy". Reviews of Modern Physics. 75 (2): 559–606. arXiv:astro-ph/0207347. Bibcode:2003RvMP...75..559P. doi:10.1103/RevModPhys.75.559. S2CID 118961123.
- ^ Weinberg, Steven (2008). Cosmology. Oxford University Press. ISBN 9780198526827.
- ^ a b Frieman, Joshua A.; Turner, Michael S.; Huterer, Dragan (2008). "Dark Energy and the Accelerating Universe". Annual Review of Astronomy and Astrophysics. 46 (1): 385–432. arXiv:0803.0982. Bibcode:2008ARA&A..46..385F. doi:10.1146/annurev.astro.46.060407.145243. S2CID 15117520.
- ^ Penzias, A. A.; Wilson, R. W. (1965). "A Measurement of Excess Antenna Temperature at 4080 Mc/s". The Astrophysical Journal. 142 (1): 419–421. Bibcode:1965ApJ...142..419P. doi:10.1086/148307.
- ^ Nemiroff, Robert J.; Patla, Bijunath (2008). "Adventures in Friedmann cosmology: A detailed expansion of the cosmological Friedmann equations". American Journal of Physics. 76 (3): 265–276. arXiv:astro-ph/0703739. Bibcode:2008AmJPh..76..265N. doi:10.1119/1.2830536. S2CID 51782808.
- ^ a b Lapuente, P. (2010). "Baryon Acoustic Oscillations". Dark Energy: Observational and Theoretical Approaches. Cambridge, UK: Cambridge University Press. Bibcode:2010deot.book.....R. ISBN 978-0521518888.
- ^ a b c Ryden, Barbara (2003). Introduction to Cosmology. San Francisco, California: Addison Wesley. p. 103. ISBN 978-0-8053-8912-8.
- ^ Albrecht, Andreas; et al. (2006). "Report of the Dark Energy Task Force". arXiv:astro-ph/0609591.
- ^ a b Riess, Adam G.; et al. (1998). "Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant". The Astronomical Journal. 116 (3): 1009–1038. arXiv:astro-ph/9805201. Bibcode:1998AJ....116.1009R. doi:10.1086/300499. S2CID 15640044.
- ^ a b c Pain, Reynald; Astier, Pierre (2012). "Observational evidence of the accelerated expansion of the Universe". Comptes Rendus Physique. 13 (6): 521–538. arXiv:1204.5493. Bibcode:2012CRPhy..13..521A. CiteSeerX 10.1.1.747.3792. doi:10.1016/j.crhy.2012.04.009. S2CID 119301091.
- ^ Lawton, Thomas (April 30, 2022). "Controversial claim that the universe is skewed could upend cosmology". New Scientist.
- ^ Jacques Colin, Roya Mohayaee, Mohamed Rameez and Subir Sarkar (Nov 2019). "Evidence for anisotropy of cosmic acceleration⋆". Astronomy & Astrophysics. 631: L13. arXiv:1808.04597. Bibcode:2019A&A...631L..13C. doi:10.1051/0004-6361/201936373. S2CID 208175643.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Sarkar, Subir (Mar 2022). "Heart of Darkness". Inference. 6 (4). doi:10.37282/991819.22.21. S2CID 247890823.
- ^ Hinshaw, G. (2009). "Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results". Astrophysical Journal Supplement. 180 (2): 225–245. arXiv:0803.0732. Bibcode:2009ApJS..180..225H. doi:10.1088/0067-0049/180/2/225. S2CID 3629998.
- ^ Eisenstein, Daniel J.; et al. (2005). "Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies". The Astrophysical Journal. 633 (2): 560–574. arXiv:astro-ph/0501171. Bibcode:2005ApJ...633..560E. doi:10.1086/466512. S2CID 4834543.
- ^ Dekel, Avishai (1999). Formation of Structure in the Universe. New York, New York: Cambridge University Press. ISBN 9780521586320.
- ^ a b c The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; The Las Cumbres Observatory Collaboration; The VINROUGE Collaboration; The MASTER Collaboration (2017-11-02). "A gravitational-wave standard siren measurement of the Hubble constant". Nature. 551 (7678): 85–88. arXiv:1710.05835. Bibcode:2017Natur.551...85A. doi:10.1038/nature24471. ISSN 0028-0836. PMID 29094696. S2CID 205261622.
{{cite journal}}: CS1 maint: numeric names: authors list (link) - ^ Abbott, B. P.; et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016-02-11). "Observation of Gravitational Waves from a Binary Black Hole Merger". Physical Review Letters. 116 (6): 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. doi:10.1103/PhysRevLett.116.061102. PMID 26918975. S2CID 119286014.
- ^ a b ur Rahman, Syed Faisal (2018-04-01). "Where next for the expanding universe?". Astronomy & Geophysics. 59 (2): 2.39–2.42. Bibcode:2018A&G....59b2.39F. doi:10.1093/astrogeo/aty088. ISSN 1366-8781.
- ^ Rosado, Pablo A.; Lasky, Paul D.; Thrane, Eric; Zhu, Xingjiang; Mandel, Ilya; Sesana, Alberto (2016). "Detectability of Gravitational Waves from High-Redshift Binaries". Physical Review Letters. 116 (10): 101102. arXiv:1512.04950. Bibcode:2016PhRvL.116j1102R. doi:10.1103/PhysRevLett.116.101102. PMID 27015470. S2CID 8736504.
- ^ Caldwell, Robert; Kamionkowski, Marc; Weinberg, Nevin (August 2003). "Phantom Energy: Dark Energy with w < −1 Causes a Cosmic Doomsday". Physical Review Letters. 91 (7): 071301. arXiv:astro-ph/0302506. Bibcode:2003PhRvL..91g1301C. doi:10.1103/PhysRevLett.91.071301. PMID 12935004. S2CID 119498512.
- ^ Caldwell, R. R. (2002). "A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state". Physics Letters B. 545 (1–2): 23–29. arXiv:astro-ph/9908168. Bibcode:2002PhLB..545...23C. doi:10.1016/S0370-2693(02)02589-3. S2CID 9820570.
- ^ University of Oxford (5 December 2018). "Bringing balance to the universe: New theory could explain missing 95 percent of the cosmos". EurekAlert!. Retrieved 6 December 2018.
- ^ Farnes, J.S. (2018). "A Unifying Theory of Dark Energy and Dark Matter: Negative Masses and Matter Creation within a Modified ΛCDM Framework". Astronomy & Astrophysics. 620: A92. arXiv:1712.07962. Bibcode:2018A&A...620A..92F. doi:10.1051/0004-6361/201832898. S2CID 53600834.
- ^ Halle, Anaelle; Zhao, Hongsheng; Li, Baojiu (2008). "Perturbations in a non-uniform dark energy fluid: equations reveal effects of modified gravity and dark matter". Astrophysical Journal Supplement Series. 177 (1): 1–13. arXiv:0711.0958. Bibcode:2008ApJS..177....1H. doi:10.1086/587744. S2CID 14155129.
- ^ Benoit-Lévy, A.; Chardin, G. (2012). "Introducing the Dirac–Milne universe". Astronomy and Astrophysics. 537 (78): A78. arXiv:1110.3054. Bibcode:2012A&A...537A..78B. doi:10.1051/0004-6361/201016103. S2CID 119232871.

- ^ Hajduković, D. S. (2012). "Quantum vacuum and virtual gravitational dipoles: the solution to the dark energy problem?". Astrophysics and Space Science. 339 (1): 1–5. arXiv:1201.4594. Bibcode:2012Ap&SS.339....1H. doi:10.1007/s10509-012-0992-y. S2CID 119257686.
- ^ Villata, M. (2013). "On the nature of dark energy: the lattice Universe". Astrophysics and Space Science. 345 (1): 1–9. arXiv:1302.3515. Bibcode:2013Ap&SS.345....1V. doi:10.1007/s10509-013-1388-3. S2CID 119288465.
- ^ Devlin, Hannah (January 25, 2020). "Has physicist's gravity theory solved 'impossible' dark energy riddle?". The Guardian.
- ^ Lombriser, Lucas; Lima, Nelson (2017). "Challenges to Self-Acceleration in Modified Gravity from Gravitational Waves and Large-Scale Structure". Physics Letters B. 765 (382): 382–385. arXiv:1602.07670. Bibcode:2017PhLB..765..382L. doi:10.1016/j.physletb.2016.12.048. S2CID 118486016.
- ^ "Quest to settle riddle over Einstein's theory may soon be over". phys.org. February 10, 2017. Retrieved October 29, 2017.
- ^ "Theoretical battle: Dark energy vs. modified gravity". Ars Technica. February 25, 2017. Retrieved October 27, 2017.
- ^ Räsänen, Syksy; Ratra, Bharat (2011). "Backreaction: directions of progress". Classical and Quantum Gravity. 28 (16): 164008. arXiv:1102.0408. Bibcode:2011CQGra..28p4008R. doi:10.1088/0264-9381/28/16/164008. S2CID 118485681.
- ^ Buchert, Thomas; Räsänen, Syksy (2012). "Backreaction in Late-Time Cosmology". Annual Review of Nuclear and Particle Science. 62 (1): 57–79. arXiv:1112.5335. Bibcode:2012ARNPS..62...57B. doi:10.1146/annurev.nucl.012809.104435. S2CID 118798287.
- ^ a b "Is dark energy an illusion?". New Scientist. 2007.
- ^ "A Cosmic 'Tardis': What the Universe Has In Common with 'Doctor Who'". Space.com. October 2013.
- ^ Wiltshire, David L. (2007). "Exact Solution to the Averaging Problem in Cosmology". Physical Review Letters. 99 (25): 251101. arXiv:0709.0732. Bibcode:2007PhRvL..99y1101W. doi:10.1103/PhysRevLett.99.251101. PMID 18233512. S2CID 1152275.
- ^ Ishak, Mustapha; Richardson, James; Garred, David; Whittington, Delilah; Nwankwo, Anthony; Sussman, Roberto (2008). "Dark Energy or Apparent Acceleration Due to a Relativistic Cosmological Model More Complex than FLRW?". Physical Review D. 78 (12): 123531. arXiv:0708.2943. Bibcode:2008PhRvD..78l3531I. doi:10.1103/PhysRevD.78.123531. S2CID 118801032.
- ^ Mattsson, Teppo (2010). "Dark energy as a mirage". General Relativity and Gravitation. 42 (3): 567–599. arXiv:0711.4264. Bibcode:2010GReGr..42..567M. doi:10.1007/s10714-009-0873-z. S2CID 14226736.
- ^ Clifton, Timothy; Ferreira, Pedro (April 2009). "Does Dark Energy Really Exist?". Scientific American. 300 (4): 48–55. Bibcode:2009SciAm.300d..48C. doi:10.1038/scientificamerican0409-48. PMID 19363920.
- ^ Wiltshire, D. (2008). "Cosmological equivalence principle and the weak-field limit". Physical Review D. 78 (8): 084032. arXiv:0809.1183. Bibcode:2008PhRvD..78h4032W. doi:10.1103/PhysRevD.78.084032. S2CID 53709630.
- ^ Gray, Stuart (2009-12-08). "Dark questions remain over dark energy". ABC Science Australia. Retrieved 27 January 2013.
- ^ Merali, Zeeya (March 2012). "Is Einstein's Greatest Work All Wrong—Because He Didn't Go Far Enough?". Discover magazine. Retrieved 27 January 2013.
- ^ Wolchover, Natalie (27 September 2011) 'Accelerating universe' could be just an illusion, NBC News
- ^ Tsagas, Christos G. (2011). "Peculiar motions, accelerated expansion, and the cosmological axis". Physical Review D. 84 (6): 063503. arXiv:1107.4045. Bibcode:2011PhRvD..84f3503T. doi:10.1103/PhysRevD.84.063503. S2CID 119179171.
- ^ Nielsen, J. T.; Guffanti, A.; Sarkar, S. (2016). "Marginal evidence for cosmic acceleration from Type Ia supernovae". Scientific Reports. 6 (35596): 35596. arXiv:1506.01354. Bibcode:2016NatSR...635596N. doi:10.1038/srep35596. PMC 5073293. PMID 27767125.
- ^ Gillespie, Stuart (21 October 2016). "The universe is expanding at an accelerating rate – or is it?". University of Oxford – News & Events – Science Blog (WP:NEWSBLOG).
- ^ Krauss, Lawrence M.; Scherrer, Robert J. (2007). "The return of a static universe and the end of cosmology". General Relativity and Gravitation. 39 (10): 1545–1550. arXiv:0704.0221. Bibcode:2007GReGr..39.1545K. doi:10.1007/s10714-007-0472-9. S2CID 123442313.
- ^ John Baez, "The End of the Universe", 7 February 2016. http://math.ucr.edu/home/baez/end.html





















