Fourier transform
| Fourier transforms |
|---|

In physics, engineering and mathematics, the Fourier transform (FT) is an integral transform that takes as input a function and outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term Fourier transform refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made the Fourier transform is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches.
Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statistics as well as in the study of physical phenomena exhibiting normal distribution (e.g., diffusion). The Fourier transform of a Gaussian function is another Gaussian function. Joseph Fourier introduced the transform in his study of heat transfer, where Gaussian functions appear as solutions of the heat equation.
The Fourier transform can be formally defined as an improper Riemann integral, making it an integral transform, although this definition is not suitable for many applications requiring a more sophisticated integration theory.[note 1] For example, many relatively simple applications use the Dirac delta function, which can be treated formally as if it were a function, but the justification requires a mathematically more sophisticated viewpoint.[note 2]
The Fourier transform can also be generalized to functions of several variables on Euclidean space, sending a function of 3-dimensional 'position space' to a function of 3-dimensional momentum (or a function of space and time to a function of 4-momentum). This idea makes the spatial Fourier transform very natural in the study of waves, as well as in quantum mechanics, where it is important to be able to represent wave solutions as functions of either position or momentum and sometimes both. In general, functions to which Fourier methods are applicable are complex-valued, and possibly vector-valued.[note 3] Still further generalization is possible to functions on groups, which, besides the original Fourier transform on R or Rn, notably includes the discrete-time Fourier transform (DTFT, group = Z), the discrete Fourier transform (DFT, group = Z mod N) and the Fourier series or circular Fourier transform (group = S1, the unit circle ≈ closed finite interval with endpoints identified). The latter is routinely employed to handle periodic functions. The fast Fourier transform (FFT) is an algorithm for computing the DFT.
Definition[edit]
The Fourier transform is an analysis process, decomposing a complex-valued function into its constituent frequencies and their amplitudes. The inverse process is synthesis, which recreates from its transform.
We can start with an analogy, the Fourier series, which analyzes on a bounded interval for some positive real number The constituent frequencies are a discrete set of harmonics at frequencies whose amplitude and phase are given by the analysis formula:
The analogy for a function can be obtained formally from the analysis formula by taking the limit as , while at the same time taking so that [1][2][3] Formally carrying this out, we obtain, for rapidly decreasing :[note 4][4]
|
|
(Eq.1)
|
It is easy to see, assuming the hypothesis of rapid decreasing, that the integral Eq.1 converges for all real , and (using the Riemann–Lebesgue lemma) that the transformed function is also rapidly decreasing. The validity of this definition for classes of functions that are not necessarily rapidly decreasing is discussed later in this section.
Evaluating Eq.1 for all values of produces the frequency-domain function. The complex number , in polar coordinates, conveys both amplitude and phase of frequency The intuitive interpretation of Eq.1 is that the effect of multiplying by is to subtract from every frequency component of function [note 5] Only the component that was at frequency can produce a non-zero value of the infinite integral, because (at least formally) all the other shifted components are oscillatory and integrate to zero. (see § Example)
The corresponding synthesis formula for such a function is:
|
|
(Eq.2)
|
Eq.2 is a representation of as a weighted summation of complex exponential functions.
This is also known as the Fourier inversion theorem, and was first introduced in Fourier's Analytical Theory of Heat.[5][6][7][8]
The functions and are referred to as a Fourier transform pair.[9] A common notation for designating transform pairs is:[10]
Definition for Lebesgue integrable functions[edit]
Until now, we have been dealing with Schwartz functions, which decay rapidly at infinity, with all derivatives. This excludes many functions of practical importance from the definition, such as the rect function. A measurable function is called (Lebesgue) integrable if the Lebesgue integral of its absolute value is finite:
Definition — The Fourier transform of a Lebesgue integrable function is defined by the formula Eq.1.
The integral Eq.1 is well-defined for all because of the assumption . (It can be shown that the function is bounded and uniformly continuous in the frequency domain, and moreover, by the Riemann–Lebesgue lemma, it is zero at infinity.)
However, the class of Lebesgue integrable functions is not ideal from the point of view of the Fourier transform because there is no easy characterization of the image, and thus no easy characterization of the inverse transform.
Unitarity and definition for square integrable functions[edit]
While Eq.1 defines the Fourier transform for (complex-valued) functions in , it is easy to see that it is not well-defined for other integrability classes, most importantly . For functions in , and with the conventions of Eq.1, the Fourier transform is a unitary operator with respect to the Hilbert inner product on , restricted to the dense subspace of integrable functions. Therefore, it admits a unique continuous extension to a unitary operator on , also called the Fourier transform. This extension is important in part because the Fourier transform preserves the space so that, unlike the case of , the Fourier transform and inverse transform are on the same footing, being transformations of the same space of functions to itself.
Importantly, for functions in , the Fourier transform is no longer given by Eq.1 (interpreted as a Lebesgue integral). For example, the function is in but not , so the integral Eq.1 diverges. In such cases, the Fourier transform can be obtained explicitly by regularizing the integral, and then passing to a limit. In practice, the integral is often regarded as an improper integral instead of a proper Lebesgue integral, but sometimes for convergence one needs to use weak limit or principal value instead of the (pointwise) limits implicit in an improper integral. Titchmarsh (1986) and Dym & McKean (1985) each gives three rigorous ways of extending the Fourier transform to square integrable functions using this procedure.
The conventions chosen in this article are those of harmonic analysis, and are characterized as the unique conventions such that the Fourier transform is both unitary on L2 and an algebra homomorphism from L1 to L∞, without renormalizing the Lebesgue measure.[12]
Angular frequency (ω)[edit]
When the independent variable () represents time (often denoted by ), the transform variable () represents frequency (often denoted by ). For example, if time is measured in seconds, then frequency is in hertz. The Fourier transform can also be written in terms of angular frequency, whose units are radians per second.
The substitution into Eq.1 produces this convention, where function is relabeled
| ordinary frequency ξ (Hz) | unitary | |
|---|---|---|
| angular frequency ω (rad/s) | unitary | |
| non-unitary |
| ordinary frequency ξ (Hz) | unitary | |
|---|---|---|
| angular frequency ω (rad/s) | unitary | |
| non-unitary |
Extension of the definition[edit]
For , the Fourier transform can be defined on by Marcinkiewicz interpolation.
The Fourier transform can be defined on domains other than the real line. The Fourier transform on Euclidean space and the Fourier transform on locally abelian groups are discussed later in the article.
The Fourier transform can also be defined for tempered distributions, dual to the space of rapidly decreasing functions (Schwartz functions). A Schwartz function is a smooth function that decays at infinity, along with all of its derivatives. The space of Schwartz functions is denoted by , and its dual is the space of tempered distributions. It is easy to see, by differentiating under the integral and applying the Riemann-Lebesgue lemma, that the Fourier transform of a Schwartz function (defined by the formula Eq.1) is again a Schwartz function. The Fourier transform of a tempered distribution is defined by duality:
Many other characterizations of the Fourier transform exist. For example, one uses the Stone–von Neumann theorem: the Fourier transform is the unique unitary intertwiner for the symplectic and Euclidean Schrödinger representations of the Heisenberg group.
Background[edit]
History[edit]
In 1822, Fourier claimed (see Joseph Fourier § The Analytic Theory of Heat) that any function, whether continuous or discontinuous, can be expanded into a series of sines.[13] That important work was corrected and expanded upon by others to provide the foundation for the various forms of the Fourier transform used since.

Complex sinusoids[edit]
In general, the coefficients are complex numbers, which have two equivalent forms (see Euler's formula):
The product with (Eq.2) has these forms:
It is noteworthy how easily the product was simplified using the polar form, and how easily the rectangular form was deduced by an application of Euler's formula.
Negative frequency[edit]
Euler's formula introduces the possibility of negative And Eq.1 is defined Only certain complex-valued have transforms (See Analytic signal. A simple example is ) But negative frequency is necessary to characterize all other complex-valued found in signal processing, partial differential equations, radar, nonlinear optics, quantum mechanics, and others.
For a real-valued Eq.1 has the symmetry property (see § Conjugation below). This redundancy enables Eq.2 to distinguish from But of course it cannot tell us the actual sign of because and are indistinguishable on just the real numbers line..
Fourier transform for periodic functions[edit]
The Fourier transform of a periodic function cannot be defined using the integral formula directly. In order for integral in Eq.1 to be defined the function must be absolutely integrable. Instead it is common to use Fourier series. It is possible to extend the definition to include periodic functions by viewing them as tempered distributions.
This makes it possible to see a connection between the Fourier series and the Fourier transform for periodic functions that have a convergent Fourier series. If is a periodic function, with period , that has a convergent Fourier series, then:
Sampling the Fourier transform[edit]
The Fourier transform of an integrable function can be sampled at regular intervals of arbitrary length These samples can be deduced from one cycle of a periodic function which has Fourier series coefficients proportional to those samples by the Poisson summation formula:
The integrability of ensures the periodic summation converges. Therefore, the samples can be determined by Fourier series analysis:
When has compact support, has a finite number of terms within the interval of integration. When does not have compact support, numerical evaluation of requires an approximation, such as tapering or truncating the number of terms.
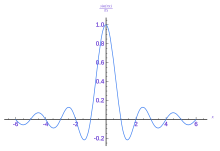
Example[edit]
The following figures provide a visual illustration of how the Fourier transform measures whether a frequency is present in a particular function. The depicted function oscillates at 3 Hz (if measures seconds) and tends quickly to 0. (The second factor in this equation is an envelope function that shapes the continuous sinusoid into a short pulse.). was specially chosen to have a real Fourier transform that can be easily plotted. The first image is its graph. In order to calculate we must integrate the product The next 2 images are the real and imaginary parts of that product. The real part of the integrand has a non-negative average value, because the alternating signs of and oscillate at the same rate and same phase, whereas and are same rate but orthogonal phase. The result is that when you integrate the real part of the integrand you get a relatively large number (in this case ). Also, when you try to measure a frequency that is not present, as in the case when we look at both real and imaginary component of the product vary rapidly between positive and negative values. Therefore, the integral is very small and the value for the Fourier transform for that frequency is nearly zero. The general situation is usually more complicated than this, but heuristically this is how the Fourier transform measures how much of an individual frequency is present in a function

-
Real and imaginary parts of integrand for Fourier transform at 5 Hz
-
Magnitude of Fourier transform, with 3 and 5 Hz labeled.
To re-enforce an earlier point, the reason for the response at Hz is because and are indistinguishable. The transform of would have just one response, whose amplitude is the integral of the smooth envelope: whereas (second graph above) is
Properties of the Fourier transform[edit]
Let and represent integrable functions Lebesgue-measurable on the real line satisfying:
Basic properties[edit]
The Fourier transform has the following basic properties:[14]
Linearity[edit]
Time shifting[edit]
Frequency shifting[edit]
Time scaling[edit]
Symmetry[edit]
When the real and imaginary parts of a complex function are decomposed into their even and odd parts, there are four components, denoted below by the subscripts RE, RO, IE, and IO. And there is a one-to-one mapping between the four components of a complex time function and the four components of its complex frequency transform:
From this, various relationships are apparent, for example:
- The transform of a real-valued function (fRE+ fRO) is the even symmetric function f̂RE+ i f̂IO. Conversely, an even-symmetric transform implies a real-valued time-domain.
- The transform of an imaginary-valued function (i fIE+ i fIO) is the odd symmetric function f̂RO+ i f̂IE, and the converse is true.
- The transform of an even-symmetric function (fRE+ i fIO) is the real-valued function f̂RE+ f̂RO, and the converse is true.
- The transform of an odd-symmetric function (fRO+ i fIE) is the imaginary-valued function i f̂IE+ i f̂IO, and the converse is true.
Conjugation[edit]
In particular, if is real, then is even symmetric (aka Hermitian function):
And if is purely imaginary, then is odd symmetric:
Real and imaginary part in time[edit]
Zero frequency component[edit]
Substituting in the definition, we obtain:
The integral of over its domain is known as the average value or DC bias of the function.
Invertibility and periodicity[edit]
Under suitable conditions on the function , it can be recovered from its Fourier transform . Indeed, denoting the Fourier transform operator by , so , then for suitable functions, applying the Fourier transform twice simply flips the function: , which can be interpreted as "reversing time". Since reversing time is two-periodic, applying this twice yields , so the Fourier transform operator is four-periodic, and similarly the inverse Fourier transform can be obtained by applying the Fourier transform three times: . In particular the Fourier transform is invertible (under suitable conditions).
More precisely, defining the parity operator such that , we have:
This fourfold periodicity of the Fourier transform is similar to a rotation of the plane by 90°, particularly as the two-fold iteration yields a reversal, and in fact this analogy can be made precise. While the Fourier transform can simply be interpreted as switching the time domain and the frequency domain, with the inverse Fourier transform switching them back, more geometrically it can be interpreted as a rotation by 90° in the time–frequency domain (considering time as the x-axis and frequency as the y-axis), and the Fourier transform can be generalized to the fractional Fourier transform, which involves rotations by other angles. This can be further generalized to linear canonical transformations, which can be visualized as the action of the special linear group SL2(R) on the time–frequency plane, with the preserved symplectic form corresponding to the uncertainty principle, below. This approach is particularly studied in signal processing, under time–frequency analysis.
Units[edit]
The frequency variable must have inverse units to the units of the original function's domain (typically named t or x). For example, if t is measured in seconds, ξ should be in cycles per second or hertz. If the scale of time is in units of 2π seconds, then another Greek letter ω typically is used instead to represent angular frequency (where ω = 2πξ) in units of radians per second. If using x for units of length, then ξ must be in inverse length, e.g., wavenumbers. That is to say, there are two versions of the real line: one which is the range of t and measured in units of t, and the other which is the range of ξ and measured in inverse units to the units of t. These two distinct versions of the real line cannot be equated with each other. Therefore, the Fourier transform goes from one space of functions to a different space of functions: functions which have a different domain of definition.
In general, ξ must always be taken to be a linear form on the space of its domain, which is to say that the second real line is the dual space of the first real line. See the article on linear algebra for a more formal explanation and for more details. This point of view becomes essential in generalizations of the Fourier transform to general symmetry groups, including the case of Fourier series.
That there is no one preferred way (often, one says "no canonical way") to compare the two versions of the real line which are involved in the Fourier transform—fixing the units on one line does not force the scale of the units on the other line—is the reason for the plethora of rival conventions on the definition of the Fourier transform. The various definitions resulting from different choices of units differ by various constants.
In other conventions, the Fourier transform has i in the exponent instead of −i, and vice versa for the inversion formula. This convention is common in modern physics[15] and is the default for Wolfram Alpha, and does not mean that the frequency has become negative, since there is no canonical definition of positivity for frequency of a complex wave. It simply means that is the amplitude of the wave instead of the wave (the former, with its minus sign, is often seen in the time dependence for Sinusoidal plane-wave solutions of the electromagnetic wave equation, or in the time dependence for quantum wave functions). Many of the identities involving the Fourier transform remain valid in those conventions, provided all terms that explicitly involve i have it replaced by −i. In Electrical engineering the letter j is typically used for the imaginary unit instead of i because i is used for current.
When using dimensionless units, the constant factors might not even be written in the transform definition. For instance, in probability theory, the characteristic function Φ of the probability density function f of a random variable X of continuous type is defined without a negative sign in the exponential, and since the units of x are ignored, there is no 2π either:
(In probability theory, and in mathematical statistics, the use of the Fourier—Stieltjes transform is preferred, because so many random variables are not of continuous type, and do not possess a density function, and one must treat not functions but distributions, i.e., measures which possess "atoms".)
From the higher point of view of group characters, which is much more abstract, all these arbitrary choices disappear, as will be explained in the later section of this article, which treats the notion of the Fourier transform of a function on a locally compact Abelian group.
Uniform continuity and the Riemann–Lebesgue lemma[edit]
The Fourier transform may be defined in some cases for non-integrable functions, but the Fourier transforms of integrable functions have several strong properties.
The Fourier transform f̂ of any integrable function f is uniformly continuous and[16]
By the Riemann–Lebesgue lemma,[17]
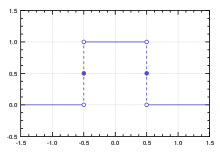
However, need not be integrable. For example, the Fourier transform of the rectangular function, which is integrable, is the sinc function, which is not Lebesgue integrable, because its improper integrals behave analogously to the alternating harmonic series, in converging to a sum without being absolutely convergent.
It is not generally possible to write the inverse transform as a Lebesgue integral. However, when both f and are integrable, the inverse equality
Plancherel theorem and Parseval's theorem[edit]
Let f(x) and g(x) be integrable, and let f̂(ξ) and ĝ(ξ) be their Fourier transforms. If f(x) and g(x) are also square-integrable, then the Parseval formula follows:[18]
The Plancherel theorem, which follows from the above, states that[19]
Plancherel's theorem makes it possible to extend the Fourier transform, by a continuity argument, to a unitary operator on L2(R). On L1(R) ∩ L2(R), this extension agrees with original Fourier transform defined on L1(R), thus enlarging the domain of the Fourier transform to L1(R) + L2(R) (and consequently to Lp(R) for 1 ≤ p ≤ 2). Plancherel's theorem has the interpretation in the sciences that the Fourier transform preserves the energy of the original quantity. The terminology of these formulas is not quite standardised. Parseval's theorem was proved only for Fourier series, and was first proved by Lyapunov. But Parseval's formula makes sense for the Fourier transform as well, and so even though in the context of the Fourier transform it was proved by Plancherel, it is still often referred to as Parseval's formula, or Parseval's relation, or even Parseval's theorem.
See Pontryagin duality for a general formulation of this concept in the context of locally compact abelian groups.
Poisson summation formula[edit]
The Poisson summation formula (PSF) is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. The Poisson summation formula says that for sufficiently regular functions f,
It has a variety of useful forms that are derived from the basic one by application of the Fourier transform's scaling and time-shifting properties. The formula has applications in engineering, physics, and number theory. The frequency-domain dual of the standard Poisson summation formula is also called the discrete-time Fourier transform.
Poisson summation is generally associated with the physics of periodic media, such as heat conduction on a circle. The fundamental solution of the heat equation on a circle is called a theta function. It is used in number theory to prove the transformation properties of theta functions, which turn out to be a type of modular form, and it is connected more generally to the theory of automorphic forms where it appears on one side of the Selberg trace formula.
Differentiation[edit]
Suppose f(x) is an absolutely continuous differentiable function, and both f and its derivative f′ are integrable. Then the Fourier transform of the derivative is given by
Analogically, , so
By applying the Fourier transform and using these formulas, some ordinary differential equations can be transformed into algebraic equations, which are much easier to solve. These formulas also give rise to the rule of thumb "f(x) is smooth if and only if f̂(ξ) quickly falls to 0 for |ξ| → ∞." By using the analogous rules for the inverse Fourier transform, one can also say "f(x) quickly falls to 0 for |x| → ∞ if and only if f̂(ξ) is smooth."
Convolution theorem[edit]
The Fourier transform translates between convolution and multiplication of functions. If f(x) and g(x) are integrable functions with Fourier transforms f̂(ξ) and ĝ(ξ) respectively, then the Fourier transform of the convolution is given by the product of the Fourier transforms f̂(ξ) and ĝ(ξ) (under other conventions for the definition of the Fourier transform a constant factor may appear).
This means that if:
In linear time invariant (LTI) system theory, it is common to interpret g(x) as the impulse response of an LTI system with input f(x) and output h(x), since substituting the unit impulse for f(x) yields h(x) = g(x). In this case, ĝ(ξ) represents the frequency response of the system.
Conversely, if f(x) can be decomposed as the product of two square integrable functions p(x) and q(x), then the Fourier transform of f(x) is given by the convolution of the respective Fourier transforms p̂(ξ) and q̂(ξ).
Cross-correlation theorem[edit]
In an analogous manner, it can be shown that if h(x) is the cross-correlation of f(x) and g(x):
As a special case, the autocorrelation of function f(x) is:
Eigenfunctions[edit]
The Fourier transform is a linear transform which has eigenfunctions obeying with
A set of eigenfunctions is found by noting that the homogeneous differential equation
More generally, a set of eigenfunctions is also found by noting that the differentiation rules imply that the ordinary differential equation
Under this convention for the Fourier transform, we have that
In other words, the Hermite functions form a complete orthonormal system of eigenfunctions for the Fourier transform on L2(R).[14][22] However, this choice of eigenfunctions is not unique. Because of there are only four different eigenvalues of the Fourier transform (the fourth roots of unity ±1 and ±i) and any linear combination of eigenfunctions with the same eigenvalue gives another eigenfunction.[23] As a consequence of this, it is possible to decompose L2(R) as a direct sum of four spaces H0, H1, H2, and H3 where the Fourier transform acts on Hek simply by multiplication by ik.
Since the complete set of Hermite functions ψn provides a resolution of the identity they diagonalize the Fourier operator, i.e. the Fourier transform can be represented by such a sum of terms weighted by the above eigenvalues, and these sums can be explicitly summed:
This approach to define the Fourier transform was first proposed by Norbert Wiener.[24] Among other properties, Hermite functions decrease exponentially fast in both frequency and time domains, and they are thus used to define a generalization of the Fourier transform, namely the fractional Fourier transform used in time–frequency analysis.[25] In physics, this transform was introduced by Edward Condon.[26] This change of basis functions becomes possible because the Fourier transform is a unitary transform when using the right conventions. Consequently, under the proper conditions it may be expected to result from a self-adjoint generator via[27]
The operator is the number operator of the quantum harmonic oscillator written as[28][29]
It can be interpreted as the generator of fractional Fourier transforms for arbitrary values of t, and of the conventional continuous Fourier transform for the particular value with the Mehler kernel implementing the corresponding active transform. The eigenfunctions of are the Hermite functions which are therefore also eigenfunctions of
Upon extending the Fourier transform to distributions the Dirac comb is also an eigenfunction of the Fourier transform.
Connection with the Heisenberg group[edit]
The Heisenberg group is a certain group of unitary operators on the Hilbert space L2(R) of square integrable complex valued functions f on the real line, generated by the translations (Ty f)(x) = f (x + y) and multiplication by ei2πξx, (Mξ f)(x) = ei2πξx f (x). These operators do not commute, as their (group) commutator is
Denote the Heisenberg group by H1. The above procedure describes not only the group structure, but also a standard unitary representation of H1 on a Hilbert space, which we denote by ρ : H1 → B(L2(R)). Define the linear automorphism of R2 by
According to the Stone–von Neumann theorem, the unitary representations ρ and ρ ∘ j are unitarily equivalent, so there is a unique intertwiner W ∈ U(L2(R)) such that
Many of the standard properties of the Fourier transform are immediate consequences of this more general framework.[30] For example, the square of the Fourier transform, W2, is an intertwiner associated with J2 = −I, and so we have (W2f)(x) = f (−x) is the reflection of the original function f.
Complex domain[edit]
The integral for the Fourier transform
The Paley–Wiener theorem says that f is smooth (i.e., n-times differentiable for all positive integers n) and compactly supported if and only if f̂ (σ + iτ) is a holomorphic function for which there exists a constant a > 0 such that for any integer n ≥ 0,
(If f is not smooth, but only L2, the statement still holds provided n = 0.[33]) The space of such functions of a complex variable is called the Paley—Wiener space. This theorem has been generalised to semisimple Lie groups.[34]
If f is supported on the half-line t ≥ 0, then f is said to be "causal" because the impulse response function of a physically realisable filter must have this property, as no effect can precede its cause. Paley and Wiener showed that then f̂ extends to a holomorphic function on the complex lower half-plane τ < 0 which tends to zero as τ goes to infinity.[35] The converse is false and it is not known how to characterise the Fourier transform of a causal function.[36]
Laplace transform[edit]
The Fourier transform f̂(ξ) is related to the Laplace transform F(s), which is also used for the solution of differential equations and the analysis of filters.
It may happen that a function f for which the Fourier integral does not converge on the real axis at all, nevertheless has a complex Fourier transform defined in some region of the complex plane.
For example, if f(t) is of exponential growth, i.e.,
The more usual version ("one-sided") of the Laplace transform is
If f is also causal, and analytical, then: Thus, extending the Fourier transform to the complex domain means it includes the Laplace transform as a special case in the case of causal functions—but with the change of variable s = i2πξ.
From another, perhaps more classical viewpoint, the Laplace transform by its form involves an additional exponential regulating term which lets it converge outside of the imaginary line where the Fourier transform is defined. As such it can converge for at most exponentially divergent series and integrals, whereas the original Fourier decomposition cannot, enabling analysis of systems with divergent or critical elements. Two particular examples from linear signal processing are the construction of allpass filter networks from critical comb and mitigating filters via exact pole-zero cancellation on the unit circle. Such designs are common in audio processing, where highly nonlinear phase response is sought for, as in reverb.
Furthermore, when extended pulselike impulse responses are sought for signal processing work, the easiest way to produce them is to have one circuit which produces a divergent time response, and then to cancel its divergence through a delayed opposite and compensatory response. There, only the delay circuit in-between admits a classical Fourier description, which is critical. Both the circuits to the side are unstable, and do not admit a convergent Fourier decomposition. However, they do admit a Laplace domain description, with identical half-planes of convergence in the complex plane (or in the discrete case, the Z-plane), wherein their effects cancel.
In modern mathematics the Laplace transform is conventionally subsumed under the aegis Fourier methods. Both of them are subsumed by the far more general, and more abstract, idea of harmonic analysis.
Inversion[edit]
Still with , if is complex analytic for a ≤ τ ≤ b, then
Theorem: If f(t) = 0 for t < 0, and |f(t)| < Cea|t| for some constants C, a > 0, then
This theorem implies the Mellin inversion formula for the Laplace transformation,[37]
The hypotheses can be weakened, as in the results of Carleson and Hunt, to f(t) e−at being L1, provided that f is of bounded variation in a closed neighborhood of t (cf. Dirichlet–Dini theorem), the value of f at t is taken to be the arithmetic mean of the left and right limits, and provided that the integrals are taken in the sense of Cauchy principal values.[39]
L2 versions of these inversion formulas are also available.[40]
Fourier transform on Euclidean space[edit]
The Fourier transform can be defined in any arbitrary number of dimensions n. As with the one-dimensional case, there are many conventions. For an integrable function f(x), this article takes the definition:
All of the basic properties listed above hold for the n-dimensional Fourier transform, as do Plancherel's and Parseval's theorem. When the function is integrable, the Fourier transform is still uniformly continuous and the Riemann–Lebesgue lemma holds.[17]
Uncertainty principle[edit]
Generally speaking, the more concentrated f(x) is, the more spread out its Fourier transform f̂(ξ) must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we squeeze a function in x, its Fourier transform stretches out in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.
The trade-off between the compaction of a function and its Fourier transform can be formalized in the form of an uncertainty principle by viewing a function and its Fourier transform as conjugate variables with respect to the symplectic form on the time–frequency domain: from the point of view of the linear canonical transformation, the Fourier transform is rotation by 90° in the time–frequency domain, and preserves the symplectic form.
Suppose f(x) is an integrable and square-integrable function. Without loss of generality, assume that f(x) is normalized:
It follows from the Plancherel theorem that f̂(ξ) is also normalized.
The spread around x = 0 may be measured by the dispersion about zero[41] defined by
In probability terms, this is the second moment of |f(x)|2 about zero.
The uncertainty principle states that, if f(x) is absolutely continuous and the functions x·f(x) and f′(x) are square integrable, then[14]
The equality is attained only in the case
In fact, this inequality implies that:
In quantum mechanics, the momentum and position wave functions are Fourier transform pairs, up to a factor of the Planck constant. With this constant properly taken into account, the inequality above becomes the statement of the Heisenberg uncertainty principle.[43]
A stronger uncertainty principle is the Hirschman uncertainty principle, which is expressed as:
Sine and cosine transforms[edit]
Fourier's original formulation of the transform did not use complex numbers, but rather sines and cosines. Statisticians and others still use this form. An absolutely integrable function f for which Fourier inversion holds can be expanded in terms of genuine frequencies (avoiding negative frequencies, which are sometimes considered hard to interpret physically[44]) λ by
This is called an expansion as a trigonometric integral, or a Fourier integral expansion. The coefficient functions a and b can be found by using variants of the Fourier cosine transform and the Fourier sine transform (the normalisations are, again, not standardised):
Older literature refers to the two transform functions, the Fourier cosine transform, a, and the Fourier sine transform, b.
The function f can be recovered from the sine and cosine transform using
Spherical harmonics[edit]
Let the set of homogeneous harmonic polynomials of degree k on Rn be denoted by Ak. The set Ak consists of the solid spherical harmonics of degree k. The solid spherical harmonics play a similar role in higher dimensions to the Hermite polynomials in dimension one. Specifically, if f(x) = e−π|x|2P(x) for some P(x) in Ak, then f̂(ξ) = i−k f(ξ). Let the set Hk be the closure in L2(Rn) of linear combinations of functions of the form f(|x|)P(x) where P(x) is in Ak. The space L2(Rn) is then a direct sum of the spaces Hk and the Fourier transform maps each space Hk to itself and is possible to characterize the action of the Fourier transform on each space Hk.[17]
Let f(x) = f0(|x|)P(x) (with P(x) in Ak), then
Here J(n + 2k − 2)/2 denotes the Bessel function of the first kind with order n + 2k − 2/2. When k = 0 this gives a useful formula for the Fourier transform of a radial function.[48] This is essentially the Hankel transform. Moreover, there is a simple recursion relating the cases n + 2 and n[49] allowing to compute, e.g., the three-dimensional Fourier transform of a radial function from the one-dimensional one.
Restriction problems[edit]
In higher dimensions it becomes interesting to study restriction problems for the Fourier transform. The Fourier transform of an integrable function is continuous and the restriction of this function to any set is defined. But for a square-integrable function the Fourier transform could be a general class of square integrable functions. As such, the restriction of the Fourier transform of an L2(Rn) function cannot be defined on sets of measure 0. It is still an active area of study to understand restriction problems in Lp for 1 < p < 2. It is possible in some cases to define the restriction of a Fourier transform to a set S, provided S has non-zero curvature. The case when S is the unit sphere in Rn is of particular interest. In this case the Tomas–Stein restriction theorem states that the restriction of the Fourier transform to the unit sphere in Rn is a bounded operator on Lp provided 1 ≤ p ≤ 2n + 2/n + 3.
One notable difference between the Fourier transform in 1 dimension versus higher dimensions concerns the partial sum operator. Consider an increasing collection of measurable sets ER indexed by R ∈ (0,∞): such as balls of radius R centered at the origin, or cubes of side 2R. For a given integrable function f, consider the function fR defined by:
Suppose in addition that f ∈ Lp(Rn). For n = 1 and 1 < p < ∞, if one takes ER = (−R, R), then fR converges to f in Lp as R tends to infinity, by the boundedness of the Hilbert transform. Naively one may hope the same holds true for n > 1. In the case that ER is taken to be a cube with side length R, then convergence still holds. Another natural candidate is the Euclidean ball ER = {ξ : |ξ| < R}. In order for this partial sum operator to converge, it is necessary that the multiplier for the unit ball be bounded in Lp(Rn). For n ≥ 2 it is a celebrated theorem of Charles Fefferman that the multiplier for the unit ball is never bounded unless p = 2.[24] In fact, when p ≠ 2, this shows that not only may fR fail to converge to f in Lp, but for some functions f ∈ Lp(Rn), fR is not even an element of Lp.
Fourier transform on function spaces[edit]
On Lp spaces[edit]
On L1[edit]
The definition of the Fourier transform by the integral formula
The Fourier transform F : L1(Rn) → L∞(Rn) is a bounded operator. This follows from the observation that
On L2[edit]
Since compactly supported smooth functions are integrable and dense in L2(Rn), the Plancherel theorem allows us to extend the definition of the Fourier transform to general functions in L2(Rn) by continuity arguments. The Fourier transform in L2(Rn) is no longer given by an ordinary Lebesgue integral, although it can be computed by an improper integral, here meaning that for an L2 function f,
Many of the properties of the Fourier transform in L1 carry over to L2, by a suitable limiting argument.
Furthermore, F : L2(Rn) → L2(Rn) is a unitary operator.[51] For an operator to be unitary it is sufficient to show that it is bijective and preserves the inner product, so in this case these follow from the Fourier inversion theorem combined with the fact that for any f, g ∈ L2(Rn) we have
In particular, the image of L2(Rn) is itself under the Fourier transform.
On other Lp[edit]
The definition of the Fourier transform can be extended to functions in Lp(Rn) for 1 ≤ p ≤ 2 by decomposing such functions into a fat tail part in L2 plus a fat body part in L1. In each of these spaces, the Fourier transform of a function in Lp(Rn) is in Lq(Rn), where q = p/p − 1 is the Hölder conjugate of p (by the Hausdorff–Young inequality). However, except for p = 2, the image is not easily characterized. Further extensions become more technical. The Fourier transform of functions in Lp for the range 2 < p < ∞ requires the study of distributions.[16] In fact, it can be shown that there are functions in Lp with p > 2 so that the Fourier transform is not defined as a function.[17]
Tempered distributions[edit]
One might consider enlarging the domain of the Fourier transform from L1 + L2 by considering generalized functions, or distributions. A distribution on Rn is a continuous linear functional on the space Cc(Rn) of compactly supported smooth functions, equipped with a suitable topology. The strategy is then to consider the action of the Fourier transform on Cc(Rn) and pass to distributions by duality. The obstruction to doing this is that the Fourier transform does not map Cc(Rn) to Cc(Rn). In fact the Fourier transform of an element in Cc(Rn) can not vanish on an open set; see the above discussion on the uncertainty principle. The right space here is the slightly larger space of Schwartz functions. The Fourier transform is an automorphism on the Schwartz space, as a topological vector space, and thus induces an automorphism on its dual, the space of tempered distributions.[17] The tempered distributions include all the integrable functions mentioned above, as well as well-behaved functions of polynomial growth and distributions of compact support.
For the definition of the Fourier transform of a tempered distribution, let f and g be integrable functions, and let f̂ and ĝ be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula,[17]
Every integrable function f defines (induces) a distribution Tf by the relation
Distributions can be differentiated and the above-mentioned compatibility of the Fourier transform with differentiation and convolution remains true for tempered distributions.
Generalizations[edit]
Fourier–Stieltjes transform[edit]
The Fourier transform of a finite Borel measure μ on Rn is given by:[52]
This transform continues to enjoy many of the properties of the Fourier transform of integrable functions. One notable difference is that the Riemann–Lebesgue lemma fails for measures.[16] In the case that dμ = f(x) dx, then the formula above reduces to the usual definition for the Fourier transform of f. In the case that μ is the probability distribution associated to a random variable X, the Fourier–Stieltjes transform is closely related to the characteristic function, but the typical conventions in probability theory take eiξx instead of e−i2πξx.[14] In the case when the distribution has a probability density function this definition reduces to the Fourier transform applied to the probability density function, again with a different choice of constants.
The Fourier transform may be used to give a characterization of measures. Bochner's theorem characterizes which functions may arise as the Fourier–Stieltjes transform of a positive measure on the circle.[16]
Furthermore, the Dirac delta function, although not a function, is a finite Borel measure. Its Fourier transform is a constant function (whose specific value depends upon the form of the Fourier transform used).
Locally compact abelian groups[edit]
The Fourier transform may be generalized to any locally compact abelian group. A locally compact abelian group is an abelian group that is at the same time a locally compact Hausdorff topological space so that the group operation is continuous. If G is a locally compact abelian group, it has a translation invariant measure μ, called Haar measure. For a locally compact abelian group G, the set of irreducible, i.e. one-dimensional, unitary representations are called its characters. With its natural group structure and the topology of uniform convergence on compact sets (that is, the topology induced by the compact-open topology on the space of all continuous functions from to the circle group), the set of characters Ĝ is itself a locally compact abelian group, called the Pontryagin dual of G. For a function f in L1(G), its Fourier transform is defined by[16]
The Riemann–Lebesgue lemma holds in this case; f̂(ξ) is a function vanishing at infinity on Ĝ.
The Fourier transform on T = R/Z is an example; here T is a locally compact abelian group, and the Haar measure μ on T can be thought of as the Lebesgue measure on [0,1). Consider the representation of T on the complex plane C that is a 1-dimensional complex vector space. There are a group of representations (which are irreducible since C is 1-dim) where for .
The character of such representation, that is the trace of for each and , is itself. In the case of representation of finite group, the character table of the group G are rows of vectors such that each row is the character of one irreducible representation of G, and these vectors form an orthonormal basis of the space of class functions that map from G to C by Schur's lemma. Now the group T is no longer finite but still compact, and it preserves the orthonormality of character table. Each row of the table is the function of and the inner product between two class functions (all functions being class functions since T is abelian) is defined as with the normalizing factor . The sequence is an orthonormal basis of the space of class functions .
For any representation V of a finite group G, can be expressed as the span ( are the irreps of G), such that . Similarly for and , . The Pontriagin dual is and for , is its Fourier transform for .
Gelfand transform[edit]
The Fourier transform is also a special case of Gelfand transform. In this particular context, it is closely related to the Pontryagin duality map defined above.
Given an abelian locally compact Hausdorff topological group G, as before we consider space L1(G), defined using a Haar measure. With convolution as multiplication, L1(G) is an abelian Banach algebra. It also has an involution * given by
Taking the completion with respect to the largest possibly C*-norm gives its enveloping C*-algebra, called the group C*-algebra C*(G) of G. (Any C*-norm on L1(G) is bounded by the L1 norm, therefore their supremum exists.)
Given any abelian C*-algebra A, the Gelfand transform gives an isomorphism between A and C0(A^), where A^ is the multiplicative linear functionals, i.e. one-dimensional representations, on A with the weak-* topology. The map is simply given by
Compact non-abelian groups[edit]
The Fourier transform can also be defined for functions on a non-abelian group, provided that the group is compact. Removing the assumption that the underlying group is abelian, irreducible unitary representations need not always be one-dimensional. This means the Fourier transform on a non-abelian group takes values as Hilbert space operators.[53] The Fourier transform on compact groups is a major tool in representation theory[54] and non-commutative harmonic analysis.
Let G be a compact Hausdorff topological group. Let Σ denote the collection of all isomorphism classes of finite-dimensional irreducible unitary representations, along with a definite choice of representation U(σ) on the Hilbert space Hσ of finite dimension dσ for each σ ∈ Σ. If μ is a finite Borel measure on G, then the Fourier–Stieltjes transform of μ is the operator on Hσ defined by
The mapping
The Peter–Weyl theorem holds, and a version of the Fourier inversion formula (Plancherel's theorem) follows: if f ∈ L2(G), then
The generalization of the Fourier transform to the noncommutative situation has also in part contributed to the development of noncommutative geometry.[citation needed] In this context, a categorical generalization of the Fourier transform to noncommutative groups is Tannaka–Krein duality, which replaces the group of characters with the category of representations. However, this loses the connection with harmonic functions.
Alternatives[edit]
In signal processing terms, a function (of time) is a representation of a signal with perfect time resolution, but no frequency information, while the Fourier transform has perfect frequency resolution, but no time information: the magnitude of the Fourier transform at a point is how much frequency content there is, but location is only given by phase (argument of the Fourier transform at a point), and standing waves are not localized in time – a sine wave continues out to infinity, without decaying. This limits the usefulness of the Fourier transform for analyzing signals that are localized in time, notably transients, or any signal of finite extent.
As alternatives to the Fourier transform, in time–frequency analysis, one uses time–frequency transforms or time–frequency distributions to represent signals in a form that has some time information and some frequency information – by the uncertainty principle, there is a trade-off between these. These can be generalizations of the Fourier transform, such as the short-time Fourier transform or fractional Fourier transform, or other functions to represent signals, as in wavelet transforms and chirplet transforms, with the wavelet analog of the (continuous) Fourier transform being the continuous wavelet transform.[25]
Applications[edit]

Linear operations performed in one domain (time or frequency) have corresponding operations in the other domain, which are sometimes easier to perform. The operation of differentiation in the time domain corresponds to multiplication by the frequency,[note 7] so some differential equations are easier to analyze in the frequency domain. Also, convolution in the time domain corresponds to ordinary multiplication in the frequency domain (see Convolution theorem). After performing the desired operations, transformation of the result can be made back to the time domain. Harmonic analysis is the systematic study of the relationship between the frequency and time domains, including the kinds of functions or operations that are "simpler" in one or the other, and has deep connections to many areas of modern mathematics.
Analysis of differential equations[edit]
Perhaps the most important use of the Fourier transformation is to solve partial differential equations. Many of the equations of the mathematical physics of the nineteenth century can be treated this way. Fourier studied the heat equation, which in one dimension and in dimensionless units is
As usual, the problem is not to find a solution: there are infinitely many. The problem is that of the so-called "boundary problem": find a solution which satisfies the "boundary conditions"
Here, f and g are given functions. For the heat equation, only one boundary condition can be required (usually the first one). But for the wave equation, there are still infinitely many solutions y which satisfy the first boundary condition. But when one imposes both conditions, there is only one possible solution.
It is easier to find the Fourier transform ŷ of the solution than to find the solution directly. This is because the Fourier transformation takes differentiation into multiplication by the Fourier-dual variable, and so a partial differential equation applied to the original function is transformed into multiplication by polynomial functions of the dual variables applied to the transformed function. After ŷ is determined, we can apply the inverse Fourier transformation to find y.
Fourier's method is as follows. First, note that any function of the forms
Second, note that therefore any integral
Now this resembles the formula for the Fourier synthesis of a function. In fact, this is the real inverse Fourier transform of a± and b± in the variable x.
The third step is to examine how to find the specific unknown coefficient functions a± and b± that will lead to y satisfying the boundary conditions. We are interested in the values of these solutions at t = 0. So we will set t = 0. Assuming that the conditions needed for Fourier inversion are satisfied, we can then find the Fourier sine and cosine transforms (in the variable x) of both sides and obtain
Similarly, taking the derivative of y with respect to t and then applying the Fourier sine and cosine transformations yields
These are four linear equations for the four unknowns a± and b±, in terms of the Fourier sine and cosine transforms of the boundary conditions, which are easily solved by elementary algebra, provided that these transforms can be found.
In summary, we chose a set of elementary solutions, parametrized by ξ, of which the general solution would be a (continuous) linear combination in the form of an integral over the parameter ξ. But this integral was in the form of a Fourier integral. The next step was to express the boundary conditions in terms of these integrals, and set them equal to the given functions f and g. But these expressions also took the form of a Fourier integral because of the properties of the Fourier transform of a derivative. The last step was to exploit Fourier inversion by applying the Fourier transformation to both sides, thus obtaining expressions for the coefficient functions a± and b± in terms of the given boundary conditions f and g.
From a higher point of view, Fourier's procedure can be reformulated more conceptually. Since there are two variables, we will use the Fourier transformation in both x and t rather than operate as Fourier did, who only transformed in the spatial variables. Note that ŷ must be considered in the sense of a distribution since y(x, t) is not going to be L1: as a wave, it will persist through time and thus is not a transient phenomenon. But it will be bounded and so its Fourier transform can be defined as a distribution. The operational properties of the Fourier transformation that are relevant to this equation are that it takes differentiation in x to multiplication by i2πξ and differentiation with respect to t to multiplication by i2πf where f is the frequency. Then the wave equation becomes an algebraic equation in ŷ:
We may as well consider the distributions supported on the conic that are given by distributions of one variable on the line ξ = f plus distributions on the line ξ = −f as follows: if Φ is any test function,
Then Fourier inversion gives, for the boundary conditions, something very similar to what we had more concretely above (put Φ(ξ, f) = ei2π(xξ+tf), which is clearly of polynomial growth):
Now, as before, applying the one-variable Fourier transformation in the variable x to these functions of x yields two equations in the two unknown distributions s± (which can be taken to be ordinary functions if the boundary conditions are L1 or L2).
From a calculational point of view, the drawback of course is that one must first calculate the Fourier transforms of the boundary conditions, then assemble the solution from these, and then calculate an inverse Fourier transform. Closed form formulas are rare, except when there is some geometric symmetry that can be exploited, and the numerical calculations are difficult because of the oscillatory nature of the integrals, which makes convergence slow and hard to estimate. For practical calculations, other methods are often used.
The twentieth century has seen the extension of these methods to all linear partial differential equations with polynomial coefficients, and by extending the notion of Fourier transformation to include Fourier integral operators, some non-linear equations as well.
Fourier-transform spectroscopy[edit]
The Fourier transform is also used in nuclear magnetic resonance (NMR) and in other kinds of spectroscopy, e.g. infrared (FTIR). In NMR an exponentially shaped free induction decay (FID) signal is acquired in the time domain and Fourier-transformed to a Lorentzian line-shape in the frequency domain. The Fourier transform is also used in magnetic resonance imaging (MRI) and mass spectrometry.
Quantum mechanics[edit]
The Fourier transform is useful in quantum mechanics in at least two different ways. To begin with, the basic conceptual structure of quantum mechanics postulates the existence of pairs of complementary variables, connected by the Heisenberg uncertainty principle. For example, in one dimension, the spatial variable q of, say, a particle, can only be measured by the quantum mechanical "position operator" at the cost of losing information about the momentum p of the particle. Therefore, the physical state of the particle can either be described by a function, called "the wave function", of q or by a function of p but not by a function of both variables. The variable p is called the conjugate variable to q. In classical mechanics, the physical state of a particle (existing in one dimension, for simplicity of exposition) would be given by assigning definite values to both p and q simultaneously. Thus, the set of all possible physical states is the two-dimensional real vector space with a p-axis and a q-axis called the phase space.
In contrast, quantum mechanics chooses a polarisation of this space in the sense that it picks a subspace of one-half the dimension, for example, the q-axis alone, but instead of considering only points, takes the set of all complex-valued "wave functions" on this axis. Nevertheless, choosing the p-axis is an equally valid polarisation, yielding a different representation of the set of possible physical states of the particle. Both representations of the wavefunction are related by a Fourier transform, such that
Physically realisable states are L2, and so by the Plancherel theorem, their Fourier transforms are also L2. (Note that since q is in units of distance and p is in units of momentum, the presence of the Planck constant in the exponent makes the exponent dimensionless, as it should be.)
Therefore, the Fourier transform can be used to pass from one way of representing the state of the particle, by a wave function of position, to another way of representing the state of the particle: by a wave function of momentum. Infinitely many different polarisations are possible, and all are equally valid. Being able to transform states from one representation to another by the Fourier transform is not only convenient but also the underlying reason of the Heisenberg uncertainty principle.
The other use of the Fourier transform in both quantum mechanics and quantum field theory is to solve the applicable wave equation. In non-relativistic quantum mechanics, Schrödinger's equation for a time-varying wave function in one-dimension, not subject to external forces, is
This is the same as the heat equation except for the presence of the imaginary unit i. Fourier methods can be used to solve this equation.
In the presence of a potential, given by the potential energy function V(x), the equation becomes
The "elementary solutions", as we referred to them above, are the so-called "stationary states" of the particle, and Fourier's algorithm, as described above, can still be used to solve the boundary value problem of the future evolution of ψ given its values for t = 0. Neither of these approaches is of much practical use in quantum mechanics. Boundary value problems and the time-evolution of the wave function is not of much practical interest: it is the stationary states that are most important.
In relativistic quantum mechanics, Schrödinger's equation becomes a wave equation as was usual in classical physics, except that complex-valued waves are considered. A simple example, in the absence of interactions with other particles or fields, is the free one-dimensional Klein–Gordon–Schrödinger–Fock equation, this time in dimensionless units,
This is, from the mathematical point of view, the same as the wave equation of classical physics solved above (but with a complex-valued wave, which makes no difference in the methods). This is of great use in quantum field theory: each separate Fourier component of a wave can be treated as a separate harmonic oscillator and then quantized, a procedure known as "second quantization". Fourier methods have been adapted to also deal with non-trivial interactions.
Finally, the number operator of the quantum harmonic oscillator can be interpreted, for example via the Mehler kernel, as the generator of the Fourier transform .[28]
Signal processing[edit]
The Fourier transform is used for the spectral analysis of time-series. The subject of statistical signal processing does not, however, usually apply the Fourier transformation to the signal itself. Even if a real signal is indeed transient, it has been found in practice advisable to model a signal by a function (or, alternatively, a stochastic process) which is stationary in the sense that its characteristic properties are constant over all time. The Fourier transform of such a function does not exist in the usual sense, and it has been found more useful for the analysis of signals to instead take the Fourier transform of its autocorrelation function.
The autocorrelation function R of a function f is defined by
This function is a function of the time-lag τ elapsing between the values of f to be correlated.
For most functions f that occur in practice, R is a bounded even function of the time-lag τ and for typical noisy signals it turns out to be uniformly continuous with a maximum at τ = 0.
The autocorrelation function, more properly called the autocovariance function unless it is normalized in some appropriate fashion, measures the strength of the correlation between the values of f separated by a time lag. This is a way of searching for the correlation of f with its own past. It is useful even for other statistical tasks besides the analysis of signals. For example, if f(t) represents the temperature at time t, one expects a strong correlation with the temperature at a time lag of 24 hours.
It possesses a Fourier transform,
This Fourier transform is called the power spectral density function of f. (Unless all periodic components are first filtered out from f, this integral will diverge, but it is easy to filter out such periodicities.)
The power spectrum, as indicated by this density function P, measures the amount of variance contributed to the data by the frequency ξ. In electrical signals, the variance is proportional to the average power (energy per unit time), and so the power spectrum describes how much the different frequencies contribute to the average power of the signal. This process is called the spectral analysis of time-series and is analogous to the usual analysis of variance of data that is not a time-series (ANOVA).
Knowledge of which frequencies are "important" in this sense is crucial for the proper design of filters and for the proper evaluation of measuring apparatuses. It can also be useful for the scientific analysis of the phenomena responsible for producing the data.
The power spectrum of a signal can also be approximately measured directly by measuring the average power that remains in a signal after all the frequencies outside a narrow band have been filtered out.
Spectral analysis is carried out for visual signals as well. The power spectrum ignores all phase relations, which is good enough for many purposes, but for video signals other types of spectral analysis must also be employed, still using the Fourier transform as a tool.
Other notations[edit]
Other common notations for include:
In the sciences and engineering it is also common to make substitutions like these:
So the transform pair can become
A disadvantage of the capital letter notation is when expressing a transform such as or which become the more awkward and
In some contexts such as particle physics, the same symbol may be used for both for a function as well as it Fourier transform, with the two only distinguished by their argument I.e. would refer to the Fourier transform because of the momentum argument, while would refer to the original function because of the positional argument. Although tildes may be used as in to indicate Fourier transforms, tildes may also be used to indicate a modification of a quantity with a more Lorentz invariant form, such as , so care must be taken. Similarly, often denotes the Hilbert transform of .
The interpretation of the complex function f̂(ξ) may be aided by expressing it in polar coordinate form
Then the inverse transform can be written:
The Fourier transform may be thought of as a mapping on function spaces. This mapping is here denoted F and F(f) is used to denote the Fourier transform of the function f. This mapping is linear, which means that F can also be seen as a linear transformation on the function space and implies that the standard notation in linear algebra of applying a linear transformation to a vector (here the function f) can be used to write F f instead of F(f). Since the result of applying the Fourier transform is again a function, we can be interested in the value of this function evaluated at the value ξ for its variable, and this is denoted either as F f(ξ) or as (F f)(ξ). Notice that in the former case, it is implicitly understood that F is applied first to f and then the resulting function is evaluated at ξ, not the other way around.
In mathematics and various applied sciences, it is often necessary to distinguish between a function f and the value of f when its variable equals x, denoted f(x). This means that a notation like F(f(x)) formally can be interpreted as the Fourier transform of the values of f at x. Despite this flaw, the previous notation appears frequently, often when a particular function or a function of a particular variable is to be transformed. For example,
Notice, that the last example is only correct under the assumption that the transformed function is a function of x, not of x0.
As discussed above, the characteristic function of a random variable is the same as the Fourier–Stieltjes transform of its distribution measure, but in this context it is typical to take a different convention for the constants. Typically characteristic function is defined
As in the case of the "non-unitary angular frequency" convention above, the factor of 2π appears in neither the normalizing constant nor the exponent. Unlike any of the conventions appearing above, this convention takes the opposite sign in the exponent.
Computation methods[edit]
The appropriate computation method largely depends how the original mathematical function is represented and the desired form of the output function.
Since the fundamental definition of a Fourier transform is an integral, functions that can be expressed as closed-form expressions are commonly computed by working the integral analytically to yield a closed-form expression in the Fourier transform conjugate variable as the result. This is the method used to generate tables of Fourier transforms,[55] including those found in the table below (Fourier transform#Tables of important Fourier transforms).
Many computer algebra systems such as Matlab and Mathematica that are capable of symbolic integration are capable of computing Fourier transforms analytically. For example, to compute the Fourier transform of cos(6πt) e−πt2 one might enter the command integrate cos(6*pi*t) exp(−pi*t^2) exp(-i*2*pi*f*t) from -inf to inf into Wolfram Alpha.[note 8]
Numerical integration of closed-form functions[edit]
If the input function is in closed-form and the desired output function is a series of ordered pairs (for example a table of values from which a graph can be generated) over a specified domain, then the Fourier transform can be generated by numerical integration at each value of the Fourier conjugate variable (frequency, for example) for which a value of the output variable is desired.[56] Note that this method requires computing a separate numerical integration for each value of frequency for which a value of the Fourier transform is desired.[57][58] The numerical integration approach works on a much broader class of functions than the analytic approach, because it yields results for functions that do not have closed form Fourier transform integrals.
Numerical integration of a series of ordered pairs[edit]
If the input function is a series of ordered pairs (for example, a time series from measuring an output variable repeatedly over a time interval) then the output function must also be a series of ordered pairs (for example, a complex number vs. frequency over a specified domain of frequencies), unless certain assumptions and approximations are made allowing the output function to be approximated by a closed-form expression. In the general case where the available input series of ordered pairs are assumed be samples representing a continuous function over an interval (amplitude vs. time, for example), the series of ordered pairs representing the desired output function can be obtained by numerical integration of the input data over the available interval at each value of the Fourier conjugate variable (frequency, for example) for which the value of the Fourier transform is desired.[59]
Explicit numerical integration over the ordered pairs can yield the Fourier transform output value for any desired value of the conjugate Fourier transform variable (frequency, for example), so that a spectrum can be produced at any desired step size and over any desired variable range for accurate determination of amplitudes, frequencies, and phases corresponding to isolated peaks. Unlike limitations in DFT and FFT methods, explicit numerical integration can have any desired step size and compute the Fourier transform over any desired range of the conjugate Fourier transform variable (for example, frequency).
Discrete Fourier transforms and fast Fourier transforms[edit]
If the ordered pairs representing the original input function are equally spaced in their input variable (for example, equal time steps), then the Fourier transform is known as a discrete Fourier transform (DFT), which can be computed either by explicit numerical integration, by explicit evaluation of the DFT definition, or by fast Fourier transform (FFT) methods. In contrast to explicit integration of input data, use of the DFT and FFT methods produces Fourier transforms described by ordered pairs of step size equal to the reciprocal of the original sampling interval. For example, if the input data is sampled every 10 seconds, the output of DFT and FFT methods will have a 0.1 Hz frequency spacing.
Tables of important Fourier transforms[edit]
The following tables record some closed-form Fourier transforms. For functions f(x) and g(x) denote their Fourier transforms by f̂ and ĝ. Only the three most common conventions are included. It may be useful to notice that entry 105 gives a relationship between the Fourier transform of a function and the original function, which can be seen as relating the Fourier transform and its inverse.
Functional relationships, one-dimensional[edit]
The Fourier transforms in this table may be found in Erdélyi (1954) or Kammler (2000, appendix).
| Function | Fourier transform unitary, ordinary frequency |
Fourier transform unitary, angular frequency |
Fourier transform non-unitary, angular frequency |
Remarks | |
|---|---|---|---|---|---|
| Definitions | |||||
| 101 | Linearity | ||||
| 102 | Shift in time domain | ||||
| 103 | Shift in frequency domain, dual of 102 | ||||
| 104 | Scaling in the time domain. If |a| is large, then f(ax) is concentrated around 0 and spreads out and flattens. | ||||
| 105 | The same transform is applied twice, but x replaces the frequency variable (ξ or ω) after the first transform. | ||||
| 106 | nth-order derivative.
As f is a Schwartz function | ||||
| 106.5 | Integration.[60] Note: is the Dirac delta function and is the average (DC) value of such that | ||||
| 107 | This is the dual of 106 | ||||
| 108 | The notation f ∗ g denotes the convolution of f and g — this rule is the convolution theorem | ||||
| 109 | This is the dual of 108 | ||||
| 110 | For f(x) purely real | Hermitian symmetry. z indicates the complex conjugate. | |||
| 113 | For f(x) purely imaginary | z indicates the complex conjugate. | |||
| 114 | Complex conjugation, generalization of 110 and 113 | ||||
| 115 | This follows from rules 101 and 103 using Euler's formula: | ||||
| 116 | This follows from 101 and 103 using Euler's formula: |
Square-integrable functions, one-dimensional[edit]
The Fourier transforms in this table may be found in Campbell & Foster (1948), Erdélyi (1954), or Kammler (2000, appendix).
| Function | Fourier transform unitary, ordinary frequency |
Fourier transform unitary, angular frequency |
Fourier transform non-unitary, angular frequency |
Remarks | |
|---|---|---|---|---|---|
| Definitions | |||||
| 201 | The rectangular pulse and the normalized sinc function, here defined as sinc(x) = sin(πx)/πx | ||||
| 202 | Dual of rule 201. The rectangular function is an ideal low-pass filter, and the sinc function is the non-causal impulse response of such a filter. The sinc function is defined here as sinc(x) = sin(πx)/πx | ||||
| 203 | The function tri(x) is the triangular function | ||||
| 204 | Dual of rule 203. | ||||
| 205 | The function u(x) is the Heaviside unit step function and a > 0. | ||||
| 206 | This shows that, for the unitary Fourier transforms, the Gaussian function e−αx2 is its own Fourier transform for some choice of α. For this to be integrable we must have Re(α) > 0. | ||||
| 208 | For Re(a) > 0. That is, the Fourier transform of a two-sided decaying exponential function is a Lorentzian function. | ||||
| 209 | Hyperbolic secant is its own Fourier transform | ||||
| 210 | Hn is the nth-order Hermite polynomial. If a = 1 then the Gauss–Hermite functions are eigenfunctions of the Fourier transform operator. For a derivation, see Hermite polynomial. The formula reduces to 206 for n = 0. |
Distributions, one-dimensional[edit]
The Fourier transforms in this table may be found in Erdélyi (1954) or Kammler (2000, appendix).
| Function | Fourier transform unitary, ordinary frequency |
Fourier transform unitary, angular frequency |
Fourier transform non-unitary, angular frequency |
Remarks | |
|---|---|---|---|---|---|
| Definitions | |||||
| 301 | The distribution δ(ξ) denotes the Dirac delta function. | ||||
| 302 | Dual of rule 301. | ||||
| 303 | This follows from 103 and 301. | ||||
| 304 | This follows from rules 101 and 303 using Euler's formula: | ||||
| 305 | This follows from 101 and 303 using | ||||
| 306 | This follows from 101 and 207 using | ||||
| 307 | This follows from 101 and 207 using | ||||
| 308 | Here it is assumed is real. For the case that alpha is complex see table entry 206 above. | ||||
| 309 | Here, n is a natural number and δ(n)(ξ) is the nth distribution derivative of the Dirac delta function. This rule follows from rules 107 and 301. Combining this rule with 101, we can transform all polynomials. | ||||
| 310 | Dual of rule 309. δ(n)(ξ) is the nth distribution derivative of the Dirac delta function. This rule follows from 106 and 302. | ||||
| 311 | Here sgn(ξ) is the sign function. Note that 1/x is not a distribution. It is necessary to use the Cauchy principal value when testing against Schwartz functions. This rule is useful in studying the Hilbert transform. | ||||
| 312 | 1/xn is the homogeneous distribution defined by the distributional derivative | ||||
| 313 | This formula is valid for 0 > α > −1. For α > 0 some singular terms arise at the origin that can be found by differentiating 320. If Re α > −1, then |x|α is a locally integrable function, and so a tempered distribution. The function α ↦ |x|α is a holomorphic function from the right half-plane to the space of tempered distributions. It admits a unique meromorphic extension to a tempered distribution, also denoted |x|α for α ≠ −1, −3, ... (See homogeneous distribution.) | ||||
| Special case of 313. | |||||
| 314 | The dual of rule 311. This time the Fourier transforms need to be considered as a Cauchy principal value. | ||||
| 315 | The function u(x) is the Heaviside unit step function; this follows from rules 101, 301, and 314. | ||||
| 316 | This function is known as the Dirac comb function. This result can be derived from 302 and 102, together with the fact that as distributions. | ||||
| 317 | The function J0(x) is the zeroth order Bessel function of first kind. | ||||
| 318 | This is a generalization of 317. The function Jn(x) is the nth order Bessel function of first kind. The function Tn(x) is the Chebyshev polynomial of the first kind. | ||||
| 319 | γ is the Euler–Mascheroni constant. It is necessary to use a finite part integral when testing 1/|ξ| or 1/|ω|against Schwartz functions. The details of this might change the coefficient of the delta function. | ||||
| 320 | This formula is valid for 1 > α > 0. Use differentiation to derive formula for higher exponents. u is the Heaviside function. |
Two-dimensional functions[edit]
| Function | Fourier transform unitary, ordinary frequency |
Fourier transform unitary, angular frequency |
Fourier transform non-unitary, angular frequency |
Remarks | |
|---|---|---|---|---|---|
| 400 | The variables ξx, ξy, ωx, ωy are real numbers. The integrals are taken over the entire plane. | ||||
| 401 | Both functions are Gaussians, which may not have unit volume. | ||||
| 402 | The function is defined by circ(r) = 1 for 0 ≤ r ≤ 1, and is 0 otherwise. The result is the amplitude distribution of the Airy disk, and is expressed using J1 (the order-1 Bessel function of the first kind).[61] | ||||
| 403 | This is the Hankel transform of r−1, a 2-D Fourier "self-transform".[62] | ||||
| 404 |
Formulas for general n-dimensional functions[edit]
| Function | Fourier transform unitary, ordinary frequency |
Fourier transform unitary, angular frequency |
Fourier transform non-unitary, angular frequency |
Remarks | |
|---|---|---|---|---|---|
| 500 | |||||
| 501 | The function χ[0, 1] is the indicator function of the interval [0, 1]. The function Γ(x) is the gamma function. The function Jn/2 + δ is a Bessel function of the first kind, with order n/2 + δ. Taking n = 2 and δ = 0 produces 402.[63] | ||||
| 502 | See Riesz potential where the constant is given by The formula also holds for all α ≠ n, n + 2, ... by analytic continuation, but then the function and its Fourier transforms need to be understood as suitably regularized tempered distributions. See homogeneous distribution.[note 9] | ||||
| 503 | This is the formula for a multivariate normal distribution normalized to 1 with a mean of 0. Bold variables are vectors or matrices. Following the notation of the aforementioned page, Σ = σ σT and Σ−1 = σ−T σ−1 | ||||
| 504 | Here[64] Re(α) > 0 |
See also[edit]
- Analog signal processing
- Beevers–Lipson strip
- Constant-Q transform
- Discrete Fourier transform
- *DFT matrix
- Fast Fourier transform
- Fourier integral operator
- Fourier inversion theorem
- Fourier multiplier
- Fourier series
- Fourier sine transform
- Fourier–Deligne transform
- Fourier–Mukai transform
- Fractional Fourier transform
- Indirect Fourier transform
- Integral transform
- Laplace transform
- Least-squares spectral analysis
- Linear canonical transform
- Mellin transform
- Multidimensional transform
- NGC 4622, especially the image NGC 4622 Fourier transform m = 2.
- Nonlocal operator
- Quantum Fourier transform
- Quadratic Fourier transform
- Short-time Fourier transform
- Spectral density
- Symbolic integration
- Time stretch dispersive Fourier transform
- Transform (mathematics)
Notes[edit]
- ^ Depending on the application a Lebesgue integral, distributional, or other approach may be most appropriate.
- ^ Vretblad (2000) provides solid justification for these formal procedures without going too deeply into functional analysis or the theory of distributions.
- ^ In relativistic quantum mechanics one encounters vector-valued Fourier transforms of multi-component wave functions. In quantum field theory, operator-valued Fourier transforms of operator-valued functions of spacetime are in frequent use, see for example Greiner & Reinhardt (1996).
- ^ For this article, a rapidly decreasing function is a function on the reals that tends to zero together with all derivatives as : . See Schwartz function.
- ^ A possible source of confusion is the frequency-shifting property; i.e. the transform of function is The value of this function at is meaning that a frequency has been shifted to zero (also see Negative frequency).
- ^ The operator is defined by replacing by in the Taylor expansion of
- ^ Up to an imaginary constant factor whose magnitude depends on what Fourier transform convention is used.
- ^ The direct command
fourier transform of cos(6*pi*t) exp(−pi*t^2)would also work for Wolfram Alpha, although the options for the convention (see Fourier transform § Other conventions) must be changed away from the default option, which is actually equivalent tointegrate cos(6*pi*t) exp(−pi*t^2) exp(i*omega*t) /sqrt(2*pi) from -inf to inf. - ^ In Gelfand & Shilov 1964, p. 363, with the non-unitary conventions of this table, the transform of is given to be
from which this follows, with .
Citations[edit]
- ^ Khare, Butola & Rajora 2023, pp. 13–14
- ^ Kaiser 1994, p. 29
- ^ Rahman 2011, p. 11
- ^ Dym & McKean 1985
- ^ Fourier 1822, p. 525
- ^ Fourier 1878, p. 408
- ^ Jordan (1883) proves on pp. 216–226 the Fourier integral theorem before studying Fourier series.
- ^ Titchmarsh 1986, p. 1
- ^ Rahman 2011, p. 10.
- ^ Oppenheim 1999, p. 58
- ^ Stein & Weiss 1971
- ^ Folland 1989
- ^ Fourier 1822
- ^ a b c d e Pinsky 2002
- ^ Arfken 1985
- ^ a b c d e Katznelson 1976
- ^ a b c d e f Stein & Weiss 1971
- ^ Rudin 1987, p. 187
- ^ Rudin 1987, p. 186
- ^ Folland 1992, p. 216
- ^ Wolf 1979, p. 307ff
- ^ Folland 1989, p. 53
- ^ Celeghini, Gadella & del Olmo 2021
- ^ a b Duoandikoetxea 2001
- ^ a b Boashash 2003
- ^ Condon 1937
- ^ Wolf 1979, p. 320
- ^ a b Wolf 1979, p. 312
- ^ Folland 1989, p. 52
- ^ Howe 1980
- ^ Paley & Wiener 1934
- ^ Gelfand & Vilenkin 1964
- ^ Kirillov & Gvishiani 1982
- ^ Clozel & Delorme 1985, pp. 331–333
- ^ de Groot & Mazur 1984, p. 146
- ^ Champeney 1987, p. 80
- ^ a b c Kolmogorov & Fomin 1999
- ^ Wiener 1949
- ^ Champeney 1987, p. 63
- ^ Widder & Wiener 1938, p. 537
- ^ Pinsky 2002, p. 131
- ^ Stein & Shakarchi 2003
- ^ Stein & Shakarchi 2003, p. 158
- ^ Chatfield 2004, p. 113
- ^ Fourier 1822, p. 441
- ^ Poincaré 1895, p. 102
- ^ Whittaker & Watson 1927, p. 188
- ^ Grafakos 2004
- ^ Grafakos & Teschl 2013
- ^ "Applied Fourier Analysis and Elements of Modern Signal Processing Lecture 3" (PDF). January 12, 2016. Retrieved 2019-10-11.
- ^ Stein & Weiss 1971, Thm. 2.3
- ^ Pinsky 2002, p. 256
- ^ Hewitt & Ross 1970, Chapter 8
- ^ Knapp 2001
- ^ Gradshteyn et al. 2015
- ^ Press et al. 1992
- ^ Bailey & Swarztrauber 1994
- ^ Lado 1971
- ^ Simonen & Olkkonen 1985
- ^ "The Integration Property of the Fourier Transform". The Fourier Transform .com. 2015 [2010]. Archived from the original on 2022-01-26. Retrieved 2023-08-20.
- ^ Stein & Weiss 1971, Thm. IV.3.3
- ^ Easton 2010
- ^ Stein & Weiss 1971, Thm. 4.15
- ^ Stein & Weiss 1971, p. 6
References[edit]
- Arfken, George (1985), Mathematical Methods for Physicists (3rd ed.), Academic Press, ISBN 9780120598205
- Bailey, David H.; Swarztrauber, Paul N. (1994), "A fast method for the numerical evaluation of continuous Fourier and Laplace transforms" (PDF), SIAM Journal on Scientific Computing, 15 (5): 1105–1110, Bibcode:1994SJSC...15.1105B, CiteSeerX 10.1.1.127.1534, doi:10.1137/0915067, archived from the original (PDF) on 2008-07-20, retrieved 2017-11-01
- Boashash, B., ed. (2003), Time–Frequency Signal Analysis and Processing: A Comprehensive Reference, Oxford: Elsevier Science, ISBN 978-0-08-044335-5
- Bochner, S.; Chandrasekharan, K. (1949), Fourier Transforms, Princeton University Press
- Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw-Hill, ISBN 978-0-07-116043-8
- Campbell, George; Foster, Ronald (1948), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc.
- Celeghini, Enrico; Gadella, Manuel; del Olmo, Mariano A. (2021), "Hermite Functions and Fourier Series", Symmetry, 13 (5): 853, arXiv:2007.10406, Bibcode:2021Symm...13..853C, doi:10.3390/sym13050853
- Champeney, D.C. (1987), A Handbook of Fourier Theorems, Cambridge University Press
- Chatfield, Chris (2004), The Analysis of Time Series: An Introduction, Texts in Statistical Science (6th ed.), London: Chapman & Hall/CRC, ISBN 9780203491683
- Clozel, Laurent; Delorme, Patrice (1985), "Sur le théorème de Paley-Wiener invariant pour les groupes de Lie réductifs réels", Comptes Rendus de l'Académie des Sciences, Série I, 300: 331–333
- Condon, E. U. (1937), "Immersion of the Fourier transform in a continuous group of functional transformations", Proc. Natl. Acad. Sci., 23 (3): 158–164, Bibcode:1937PNAS...23..158C, doi:10.1073/pnas.23.3.158, PMC 1076889, PMID 16588141
- de Groot, Sybren R.; Mazur, Peter (1984), Non-Equilibrium Thermodynamics (2nd ed.), New York: Dover
- Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 978-0-8218-2172-5
- Dym, H.; McKean, H. (1985), Fourier Series and Integrals, Academic Press, ISBN 978-0-12-226451-1
- Easton, Roger L. Jr. (2010), Fourier Methods in Imaging, John Wiley & Sons, ISBN 978-0-470-68983-7, retrieved 26 May 2020
- Erdélyi, Arthur, ed. (1954), Tables of Integral Transforms, vol. 1, McGraw-Hill
- Feller, William (1971), An Introduction to Probability Theory and Its Applications, vol. II (2nd ed.), New York: Wiley, MR 0270403
- Folland, Gerald (1989), Harmonic analysis in phase space, Princeton University Press
- Folland, Gerald (1992), Fourier analysis and its applications, Wadsworth & Brooks/Cole
- Fourier, J.B. Joseph (1822), Théorie analytique de la chaleur (in French), Paris: Firmin Didot, père et fils, OCLC 2688081
- Fourier, J.B. Joseph (1878) [1822], The Analytical Theory of Heat, translated by Alexander Freeman, The University Press (translated from French)
- Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich; Geronimus, Yuri Veniaminovich; Tseytlin, Michail Yulyevich; Jeffrey, Alan (2015), Zwillinger, Daniel; Moll, Victor Hugo (eds.), Table of Integrals, Series, and Products, translated by Scripta Technica, Inc. (8th ed.), Academic Press, ISBN 978-0-12-384933-5
- Grafakos, Loukas (2004), Classical and Modern Fourier Analysis, Prentice-Hall, ISBN 978-0-13-035399-3
- Grafakos, Loukas; Teschl, Gerald (2013), "On Fourier transforms of radial functions and distributions", J. Fourier Anal. Appl., 19: 167–179, arXiv:1112.5469, doi:10.1007/s00041-012-9242-5, S2CID 1280745
- Greiner, W.; Reinhardt, J. (1996), Field Quantization, Springer, ISBN 978-3-540-59179-5
- Gelfand, I.M.; Shilov, G.E. (1964), Generalized Functions, vol. 1, New York: Academic Press (translated from Russian)
- Gelfand, I.M.; Vilenkin, N.Y. (1964), Generalized Functions, vol. 4, New York: Academic Press (translated from Russian)
- Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis, Die Grundlehren der mathematischen Wissenschaften, Band 152, vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Springer, MR 0262773
- Hörmander, L. (1976), Linear Partial Differential Operators, vol. 1, Springer, ISBN 978-3-540-00662-6
- Howe, Roger (1980), "On the role of the Heisenberg group in harmonic analysis", Bulletin of the American Mathematical Society, 3 (2): 821–844, doi:10.1090/S0273-0979-1980-14825-9, MR 0578375
- James, J.F. (2011), A Student's Guide to Fourier Transforms (3rd ed.), Cambridge University Press, ISBN 978-0-521-17683-5
- Jordan, Camille (1883), Cours d'Analyse de l'École Polytechnique, vol. II, Calcul Intégral: Intégrales définies et indéfinies (2nd ed.), Paris
{{citation}}: CS1 maint: location missing publisher (link) - Kaiser, Gerald (1994), "A Friendly Guide to Wavelets", Physics Today, 48 (7): 57–58, Bibcode:1995PhT....48g..57K, doi:10.1063/1.2808105, ISBN 978-0-8176-3711-8
- Kammler, David (2000), A First Course in Fourier Analysis, Prentice Hall, ISBN 978-0-13-578782-3
- Katznelson, Yitzhak (1976), An Introduction to Harmonic Analysis, Dover, ISBN 978-0-486-63331-2
- Khare, Kedar; Butola, Mansi; Rajora, Sunaina (2023), "Chapter 2.3 Fourier Transform as a Limiting Case of Fourier Series", Fourier Optics and Computational Imaging (2nd ed.), Springer, doi:10.1007/978-3-031-18353-9, ISBN 978-3-031-18353-9, S2CID 255676773
- Kirillov, Alexandre; Gvishiani, Alexei D. (1982) [1979], Theorems and Problems in Functional Analysis, Springer (translated from Russian)
- Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4
- Kolmogorov, Andrey Nikolaevich; Fomin, Sergei Vasilyevich (1999) [1957], Elements of the Theory of Functions and Functional Analysis, Dover (translated from Russian)
- Lado, F. (1971), "Numerical Fourier transforms in one, two, and three dimensions for liquid state calculations", Journal of Computational Physics, 8 (3): 417–433, Bibcode:1971JCoPh...8..417L, doi:10.1016/0021-9991(71)90021-0
- Müller, Meinard (2015), The Fourier Transform in a Nutshell. (PDF), Springer, doi:10.1007/978-3-319-21945-5, ISBN 978-3-319-21944-8, S2CID 8691186; also available at Fundamentals of Music Processing, Section 2.1, pages 40–56
- Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999), Discrete-time signal processing (2nd ed.), Upper Saddle River, N.J.: Prentice Hall, ISBN 0-13-754920-2
- Paley, R.E.A.C.; Wiener, Norbert (1934), Fourier Transforms in the Complex Domain, American Mathematical Society Colloquium Publications, Providence, Rhode Island: American Mathematical Society
- Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 978-0-534-37660-4
- Poincaré, Henri (1895), Théorie analytique de la propagation de la chaleur, Paris: Carré
- Polyanin, A. D.; Manzhirov, A. V. (1998), Handbook of Integral Equations, Boca Raton: CRC Press, ISBN 978-0-8493-2876-3
- Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (1992), Numerical Recipes in C: The Art of Scientific Computing, Second Edition (2nd ed.), Cambridge University Press
- Proakis, John G.; Manolakis, Dimitri G. (1996). Digital Signal Processing: Principles, Algorithms and Applications (3 ed.). New Jersey: Prentice-Hall International. Bibcode:1996dspp.book.....P. ISBN 9780133942897. sAcfAQAAIAAJ.
- Rahman, Matiur (2011), Applications of Fourier Transforms to Generalized Functions, WIT Press, ISBN 978-1-84564-564-9
- Rudin, Walter (1987), Real and Complex Analysis (3rd ed.), Singapore: McGraw Hill, ISBN 978-0-07-100276-9
- Simonen, P.; Olkkonen, H. (1985), "Fast method for computing the Fourier integral transform via Simpson's numerical integration", Journal of Biomedical Engineering, 7 (4): 337–340, doi:10.1016/0141-5425(85)90067-6, PMID 4057997
- Smith, Julius O. "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition". ccrma.stanford.edu. Retrieved 2022-12-29.
We may think of a real sinusoid as being the sum of a positive-frequency and a negative-frequency complex sinusoid.
- Stein, Elias; Shakarchi, Rami (2003), Fourier Analysis: An introduction, Princeton University Press, ISBN 978-0-691-11384-5
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9
- Taneja, H.C. (2008), "Chapter 18: Fourier integrals and Fourier transforms", Advanced Engineering Mathematics, vol. 2, New Delhi, India: I. K. International Pvt Ltd, ISBN 978-8189866563
- Titchmarsh, E. (1986) [1948], Introduction to the theory of Fourier integrals (2nd ed.), Oxford University: Clarendon Press, ISBN 978-0-8284-0324-5
- Vretblad, Anders (2000), Fourier Analysis and its Applications, Graduate Texts in Mathematics, vol. 223, New York: Springer, ISBN 978-0-387-00836-3
- Whittaker, E. T.; Watson, G. N. (1927), A Course of Modern Analysis (4th ed.), Cambridge University Press
- Widder, David Vernon; Wiener, Norbert (August 1938), "Remarks on the Classical Inversion Formula for the Laplace Integral", Bulletin of the American Mathematical Society, 44 (8): 573–575, doi:10.1090/s0002-9904-1938-06812-7
- Wiener, Norbert (1949), Extrapolation, Interpolation, and Smoothing of Stationary Time Series With Engineering Applications, Cambridge, Mass.: Technology Press and John Wiley & Sons and Chapman & Hall
- Wilson, R. G. (1995), Fourier Series and Optical Transform Techniques in Contemporary Optics, New York: Wiley, ISBN 978-0-471-30357-2
- Wolf, Kurt B. (1979), Integral Transforms in Science and Engineering, Springer, doi:10.1007/978-1-4757-0872-1, ISBN 978-1-4757-0874-5
- Yosida, K. (1968), Functional Analysis, Springer, ISBN 978-3-540-58654-8
External links[edit]
 Media related to Fourier transformation at Wikimedia Commons
Media related to Fourier transformation at Wikimedia Commons- Encyclopedia of Mathematics
- Weisstein, Eric W. "Fourier Transform". MathWorld.
- Fourier Transform in Crystallography











![{\displaystyle \textstyle x\in [-P/2,P/2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be4c2043b276e0f129991362775e5c5beff8982)



![{\displaystyle f(x)=\sum _{n=-\infty }^{\infty }c_{n}\,e^{i2\pi {\tfrac {n}{P}}x},\quad \textstyle x\in [-P/2,P/2].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/179ca2af800697798c172e1b58a650fbe2a1ccc6)






































































































































![{\displaystyle {\mathcal {F}}[\psi ]=\lambda \psi ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb312a1e0c7fe50ae6f17f3b157e13671bdd307e)

![{\displaystyle \left[U\left({\frac {1}{2\pi }}{\frac {d}{dx}}\right)+U(x)\right]\psi (x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbdeac78597b20e0cc63dafce13269df2332ca31)






![{\displaystyle \left[W\left({\frac {i}{2\pi }}{\frac {d}{dx}}\right)+W(x)\right]\psi (x)=C\psi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d064e51b07fbf1e010b2aacf43bf894c516e0c92)



![{\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)



=\int dxf(x)\sum _{n\geq 0}(-i)^{n}\psi _{n}(x)\psi _{n}(\xi )~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eada95a2763cb70e97d43afd2f1f557fd2f046b)

![{\displaystyle {\mathcal {F}}[\psi ]=e^{-itN}\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/271ffa7285358aed34c7ccbdadcc08d3da01dd90)
















































































![{\displaystyle {\begin{aligned}y(x,t)=\int _{0}^{\infty }d\xi {\Bigl [}&a_{+}(\xi )\cos {\bigl (}2\pi \xi (x+t){\bigr )}+a_{-}(\xi )\cos {\bigl (}2\pi \xi (x-t){\bigr )}+{}\\&b_{+}(\xi )\sin {\bigl (}2\pi \xi (x+t){\bigr )}+b_{-}(\xi )\sin \left(2\pi \xi (x-t)\right){\Bigr ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a65c9bf34f6bc5abac0d29243bda58f8c3310c2d)
















































































































































































































































![{\displaystyle \chi _{[0,1]}(|\mathbf {x} |)\left(1-|\mathbf {x} |^{2}\right)^{\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f3e6c1f52f0ee9366c40ee6f67c65f11dbd03a)




























