List of metaphor-based metaheuristics
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages)
|
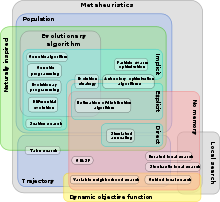
This is a chronologically ordered list of metaphor-based metaheuristics and swarm intelligence algorithms, sorted by decade of proposal.
Algorithms[edit]
1980s-1990s[edit]
Simulated annealing (Kirkpatrick et al., 1983)[edit]

Simulated annealing is a probabilistic algorithm inspired by annealing, a heat treatment method in metallurgy. It is often used when the search space is discrete (e.g., all tours that visit a given set of cities). For problems where finding the precise global optimum is less important than finding an acceptable local optimum in a fixed amount of time, simulated annealing may be preferable to alternatives such as gradient descent.
The analogue of the slow cooling of annealing is a slow decrease in the probability of simulated annealing accepting worse solutions as it explores the solution space. Accepting worse solutions is a fundamental property of metaheuristics because it allows for a more extensive search for the optimal solution.
Ant colony optimization (ACO) (Dorigo, 1992)[edit]
The ant colony optimization algorithm is a probabilistic technique for solving computational problems that can be reduced to finding good paths through graphs. Initially proposed by Marco Dorigo in 1992 in his PhD thesis,[1][2] the first algorithm aimed to search for an optimal path in a graph based on the behavior of ants seeking a path between their colony and a source of food. The original idea has since diversified to solve a wider class of numerical problems, and as a result, several problems[example needed] have emerged, drawing on various aspects of the behavior of ants. From a broader perspective, ACO performs a model-based search[3] and shares some similarities with the estimation of distribution algorithms.
Particle swarm optimization (PSO) (Kennedy & Eberhart, 1995)[edit]
Particle swarm optimization is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, dubbed particles, and moving these particles around in the search space according to simple mathematical formulae[which?] over the particle's position and velocity. Each particle's movement is influenced by its local best known position but is also guided toward the best-known positions in the search space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
PSO is originally attributed to Kennedy, Eberhart and Shi[4][5] and was first intended for simulating social behaviour[6] as a stylized representation of the movement of organisms in a bird flock or fish school. The algorithm was simplified, and it was observed to be performing optimization. The book by Kennedy and Eberhart[7] describes many philosophical aspects of PSO and swarm intelligence. An extensive survey of PSO applications is made by Poli.[8][9] A comprehensive review of theoretical and experimental works on PSO has been published by Bonyadi and Michalewicz.[10]
2000s[edit]
Harmony search (HS) (Geem, Kim & Loganathan, 2001)[edit]
Harmony search is a phenomenon-mimicking metaheuristic introduced in 2001 by Zong Woo Geem, Joong Hoon Kim, and G. V. Loganathan[11] and is inspired by the improvization process of jazz musicians. In the HS algorithm, a set of possible solutions is randomly generated (called Harmony memory). A new solution is generated by using all the solutions in the Harmony memory (rather than just two as used in GA) and if this new solution is better than the worst solution in Harmony memory, the worst solution gets replaced by this new solution. The effectiveness and advantages of HS have been demonstrated in various applications like design of municipal water distribution networks,[12] structural design,[13] load dispatch problem in electrical engineering,[14] multi-objective optimization,[15] rostering problems,[16] clustering,[17] and classification and feature selection.[18][19] A detailed survey on applications of HS can be found.[20][21] and applications of HS in data mining can be found in.[22]
Dennis (2015) claimed that harmony search is a special case of the evolution strategies algorithm.[23] However, Saka et al. (2016) argues that the structure of evolution strategies is different from that of harmony search.[24]
Artificial bee colony algorithm (Karaboga, 2005)[edit]
Artificial bee colony algorithm is a metaheuristic introduced by Karaboga in 2005[25] which simulates the foraging behaviour of honey bees. The ABC algorithm has three phases: employed bee, onlooker bee and scout bee. In the employed bee and the onlooker bee phases, bees exploit the sources by local searches in the neighbourhood of the solutions selected based on deterministic selection in the employed bee phase and the probabilistic selection in the onlooker bee phase. In the scout bee phase, which is analogous to bees abandoning exhausted food sources in the foraging process, solutions that are not beneficial anymore for search progress are abandoned, and new solutions are inserted instead to explore new regions in the search space. The algorithm has a well-balanced[weasel words] exploration and exploitation ability.[clarification needed]
Bees algorithm (Pham, 2005)[edit]
The bees algorithm was formulated by Pham and his co-workers in 2005[26] and further refined in 2009.[27] Modelled on the foraging behaviour of honey bees, the algorithm combines global explorative search with local exploitative search. A small number of artificial bees (scouts) explores randomly the solution space (environment) for solutions of high fitness (highly profitable food sources), whilst the bulk of the population search (harvest) the neighbourhood of the fittest solutions looking for the fitness optimum. A deterministic recruitment procedure which simulates the waggle dance of biological bees is used to communicate the scouts' findings to the foragers and distribute the foragers depending on the fitness of the neighbourhoods selected for local search. Once the search in the neighbourhood of a solution stagnates, the local fitness optimum is considered to be found, and the site is abandoned.
Imperialist competitive algorithm (Atashpaz-Gargari & Lucas, 2007)[edit]
The imperialist competitive algorithm (ICA), like most of the methods in the area of evolutionary computation, does not need the gradient of the function in its optimization process. From a specific point of view, ICA can be thought of as the social counterpart of genetic algorithms (GAs). ICA is the mathematical model and the computer simulation of human social evolution, while GAs is based on the biological evolution of species.
This algorithm starts by generating a set of random candidate solutions in the search space of the optimization problem. The generated random points are called the initial Countries. Countries in this algorithm are the counterpart of Chromosomes in GAs and Particles in Particle Swarm Optimization and it is an array of values of a candidate solution of optimization problem. The cost function of the optimization problem determines the power of each country. Based on their power, some of the best initial countries (the countries with the least cost function value), become Imperialists and start taking control of other countries (called colonies) and form the initial Empires.[28]
Two main operators of this algorithm are Assimilation and Revolution. Assimilation makes the colonies of each empire get closer to the imperialist state in the space of socio-political characteristics (optimization search space). Revolution brings about sudden random changes in the position of some of the countries in the search space. During assimilation and revolution, a colony might reach a better position and then have a chance to take the control of the entire empire and replace the current imperialist state of the empire.[29]
Imperialistic Competition is another part of this algorithm. All the empires try to win this game and take possession of colonies of other empires. In each step of the algorithm, based on their power, all the empires have a chance to take control of one or more of the colonies of the weakest empire.[28]
The algorithm continues with the mentioned steps (Assimilation, Revolution, Competition) until a stop condition is satisfied.
The above steps can be summarized as the below pseudocode:[30][29]
0) Define objective function:
1) Initialization of the algorithm. Generate some random solution in the search space and create initial empires.
2) Assimilation: Colonies move towards imperialist states in different in directions.
3) Revolution: Random changes occur in the characteristics of some countries.
4) Position exchange between a colony and Imperialist. A colony with a better position than the imperialist,
has the chance to take the control of empire by replacing the existing imperialist.
5) Imperialistic competition: All imperialists compete to take possession of colonies of each other.
6) Eliminate the powerless empires. Weak empires lose their power gradually and they will finally be eliminated.
7) If the stop condition is satisfied, stop, if not go to 2.
8) End
River formation dynamics (Rabanal, Rodríguez & Rubio, 2007)[edit]
River formation dynamics is based on imitating how water forms rivers by eroding the ground and depositing sediments (the drops act as the swarm). After drops transform the landscape by increasing/decreasing the altitude of places, solutions are given in the form of paths of decreasing altitudes. Decreasing gradients are constructed, and these gradients are followed by subsequent drops to compose new gradients and reinforce the best ones. This heuristic optimization method was proposed in 2007 by Rabanal et al.[31] The applicability of RFD to other NP-complete problems has been studied,[32] and the algorithm has been applied to fields such as routing[33] and robot navigation.[34] The main applications of RFD can be found at the survey Rabanal et al. (2017).[35]
Gravitational search algorithm (Rashedi, Nezamabadi-pour & Saryazdi, 2009)[edit]
The gravitational search algorithm is based on the law of gravity and the notion of mass interactions. The GSA algorithm uses the theory of Newtonian physics and its searcher agents are the collection of masses. In GSA, there is an isolated system of masses. Using the gravitational force, every mass in the system can see the situation of other masses. The gravitational force is therefore a way of transferring information between different masses.[36] In GSA, agents are considered as objects and their performance is measured by their masses. All these objects attract each other by a gravity force, and this force causes movement of all objects towards the objects with heavier masses. Heavier masses correspond to better solutions of the problem. The position of the agent corresponds to a solution of the problem, and its mass is determined using a fitness function. By lapse of time, masses are attracted by the heaviest mass, which would ideally present an optimum solution in the search space. The GSA could be considered as a small artificial world of masses obeying the Newtonian laws of gravitation and motion.[37] A multi-objective variant of GSA, called MOGSA, was proposed by Hassanzadeh et al. in 2010.[38]
2010s[edit]
Bat algorithm (Yang, 2010)[edit]
Bat algorithm is a swarm-intelligence-based algorithm, inspired by the echolocation behavior of microbats. BA automatically balances exploration (long-range jumps around the global search space to avoid getting stuck around one local maximum) with exploitation (searching in more detail around known good solutions to find local maxima) by controlling loudness and pulse emission rates of simulated bats in the multi-dimensional search space.[39]
Spiral optimization (SPO) algorithm (Tamura & Yasuda 2011, 2016-2017)[edit]

The spiral optimization algorithm, inspired by spiral phenomena in nature, is a multipoint search algorithm that has no objective function gradient. It uses multiple spiral models that can be described as deterministic dynamical systems. As search points follow logarithmic spiral trajectories towards the common center, defined as the current best point, better solutions can be found, and the common center can be updated.[40]
Artificial swarm intelligence (Rosenberg, 2014)[edit]
Artificial swarm intelligence is a real-time closed-loop system of human users connected over the internet and structured in a framework modeled after natural swarms such that it evokes the group's collective wisdom as a unified emergent intelligence.[41][42] In this way, human swarms can answer questions, make predictions, reach decisions, and solve problems by collectively exploring a diverse set of options and converging on preferred solutions in synchrony. Invented by Dr. Louis Rosenberg in 2014, the ASI methodology has been noted for its ability to make accurate collective predictions that outperform the individual members of the swarm.[43] In 2016, an Artificial Swarm Intelligence group from Unanimous A.I. was challenged by a reporter to predict the winners of the Kentucky Derby; it successfully picked the first four horses, in order, beating 540 to 1 odds.[44][45]
Self-tuning metaheuristics[edit]
Self-tuning metaheuristics have emerged as a significant advancement in the field of optimization algorithms in recent years, since fine tuning can be a very long and difficult process.[46] These algorithms differentiate themselves by their ability to autonomously adjust their parameters in response to the problem at hand, enhancing efficiency and solution quality. This self-tuning capability is particularly important in complex optimization scenarios where traditional methods may struggle due to rigid parameter settings. In this attempt, a PSO variant has already been introduced that adopts fuzzy logic to automatically calculate the parameters of each particle[47] as well as the Flying fox optimization which is a fuzzy self tuning optimizer.[48]
The advent of self-tuning variants in metaheuristics, marks a pivotal shift towards more autonomous optimization tools. These self-tuning algorithms significantly reduce the need for expert intervention in parameter tuning, a process requiring extensive domain knowledge. By leveraging fuzzy logic and other adaptive mechanisms, these algorithms can intelligently adjust their parameters in response to the problem's characteristics and search space dynamics. This autonomy not only simplifies the optimization process but also broadens the applicability of these algorithms, making them more accessible and effective for a wider range of users and complex problems. The ability of these self-tuning metaheuristics to perform effectively without perfect tuning by the user represents a considerable advancement in making optimization more user-friendly and efficient.
Criticism of the metaphor methodology[edit]
While individual metaphor-inspired metaheuristics have produced remarkably effective solutions to specific problems,[49] metaphor-inspired metaheuristics in general have attracted criticism among researchers for hiding their lack of effectiveness or novelty behind elaborate metaphors.[49][50] Kenneth Sörensen noted:[51]
In recent years, the field of combinatorial optimization has witnessed a true tsunami of "novel" metaheuristic methods, most of them based on a metaphor of some natural or man-made process. The behavior of virtually any species of insects, the flow of water, musicians playing together – it seems that no idea is too far-fetched to serve as inspiration to launch yet another metaheuristic. [I] will argue that this line of research is threatening to lead the area of metaheuristics away from scientific rigor.
Sörensen and Glover stated:[52]
A large (and increasing) number of publications focuses on the development of (supposedly) new metaheuristic frameworks based on metaphors. The list of natural or man-made processes that has been used as the basis for a metaheuristic framework now includes such diverse processes as bacterial foraging, river formation, biogeography, musicians playing together, electromagnetism, gravity, colonization by an empire, mine blasts, league championships, clouds, and so forth. An important subcategory is found in metaheuristics based on animal behavior. Ants, bees, bats, wolves, cats, fireflies, eagles, dolphins, frogs, salmon, vultures, termites, flies, and many others, have all been used to inspire a "novel" metaheuristic. [...] As a general rule, publication of papers on metaphor-based metaheuristics has been limited to second-tier journals and conferences, but some recent exceptions to this rule can be found. Sörensen (2013) states that research in this direction is fundamentally flawed. Most importantly, the author contends that the novelty of the underlying metaphor does not automatically render the resulting framework "novel". On the contrary, there is increasing evidence that very few of the metaphor-based methods are new in any interesting sense.
In response, Springer's Journal of Heuristics has updated their editorial policy to state:[53]
Proposing new paradigms is only acceptable if they contain innovative basic ideas, such as those that are embedded in classical frameworks like genetic algorithms, tabu search, and simulated annealing. The Journal of Heuristics avoids the publication of articles that repackage and embed old ideas in methods that are claimed to be based on metaphors of natural or manmade systems and processes. These so-called "novel" methods employ analogies that range from intelligent water drops, musicians playing jazz, imperialist societies, leapfrogs, kangaroos, all types of swarms and insects and even mine blast processes (Sörensen, 2013). If a researcher uses a metaphor to stimulate his or her own ideas about a new method, the method must nevertheless be translated into metaphor-free language, so that the strategies employed can be clearly understood, and their novelty is made clearly visible. (See items 2 and 3 below.) Metaphors are cheap and easy to come by. Their use to "window dress" a method is not acceptable."
[...] Implementations should be explained by employing standard optimization terminology, where a solution is called a "solution" and not something else related to some obscure metaphor (e.g., harmony, flies, bats, countries, etc.).
[...] The Journal of Heuristics fully endorses Sörensen's view that metaphor-based “novel” methods should not be published if they cannot demonstrate a contribution to their field. Renaming existing concepts does not count as a contribution. Even though these methods are often called “novel”, many present no new ideas, except for the occasional marginal variant of an already existing methodology. These methods should not take the journal space of truly innovative ideas and research. Since they do not use the standard optimization vocabulary, they are unnecessarily difficult to understand.
The policy of Springer's journal 4OR - A Quarterly Journal of Operations Research states:[54]
The emphasis on scientific rigor and on innovation implies, in particular, that the journal does not publish articles that simply propose disguised variants of known methods without adequate validation (e.g., metaheuristics that are claimed to be "effective" on the sole basis of metaphorical comparisons with natural or artificial systems and processes). New methods must be presented in metaphor-free language by establishing their relationship with classical paradigms. Their properties must be established on the basis of scientifically compelling arguments: mathematical proofs, controlled experiments, objective comparisons, etc.
The ACM Transactions on Evolutionary Learning Optimization and the Evolutionary Computation journal also include similar statements[55][56].
See also[edit]
Notes[edit]
- ^ Colorni, Alberto; Dorigo, Marco; Maniezzo, Vittorio (1992). "Distributed Optimization by Ant Colonies". In Varela, Francisco J.; Bourgine, Paul (eds.). Toward a Practice of Autonomous Systems: Proceedings of the First European Conference on Artificial Life. pp. 134–42. ISBN 978-0-262-72019-9.
- ^ M. Dorigo, Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italy, 1992.[page needed]
- ^ Zlochin, Mark; Birattari, Mauro; Meuleau, Nicolas; Dorigo, Marco (2004). "Model-Based Search for Combinatorial Optimization: A Critical Survey". Annals of Operations Research. 131 (1–4): 373–95. CiteSeerX 10.1.1.3.427. doi:10.1023/B:ANOR.0000039526.52305.af. S2CID 63137.
- ^ Kennedy, J.; Eberhart, R. (1995). "Particle swarm optimization". Proceedings of ICNN'95 - International Conference on Neural Networks. Vol. 4. pp. 1942–8. CiteSeerX 10.1.1.709.6654. doi:10.1109/ICNN.1995.488968. ISBN 978-0-7803-2768-9. S2CID 7367791.
- ^ Shi, Y.; Eberhart, R. (1998). "A modified particle swarm optimizer". 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360). pp. 69–73. doi:10.1109/ICEC.1998.699146. ISBN 978-0-7803-4869-1. S2CID 16708577.
- ^ Kennedy, J. (1997). "The particle swarm: Social adaptation of knowledge". Proceedings of 1997 IEEE International Conference on Evolutionary Computation (ICEC '97). pp. 303–8. doi:10.1109/ICEC.1997.592326. ISBN 978-0-7803-3949-1. S2CID 61487376.
- ^ Kennedy, J.; Eberhart, R.C. (2001). Swarm Intelligence. Morgan Kaufmann. ISBN 978-1-55860-595-4.
- ^ Poli, R. (2007). "An analysis of publications on particle swarm optimisation applications" (PDF). Technical Report CSM-469. Department of Computer Science, University of Essex, UK. Archived from the original (PDF) on 2011-07-16. Retrieved 2016-08-31.
- ^ Poli, Riccardo (2008). "Analysis of the Publications on the Applications of Particle Swarm Optimisation". Journal of Artificial Evolution and Applications. 2008: 1–10. doi:10.1155/2008/685175.
- ^ Bonyadi, Mohammad Reza; Michalewicz, Zbigniew (2017). "Particle Swarm Optimization for Single Objective Continuous Space Problems: A Review". Evolutionary Computation. 25 (1): 1–54. doi:10.1162/EVCO_r_00180. PMID 26953883. S2CID 8783143.
- ^ Zong Woo Geem; Joong Hoon Kim; Loganathan, G.V. (2016). "A New Heuristic Optimization Algorithm: Harmony Search". Simulation. 76 (2): 60–8. doi:10.1177/003754970107600201. S2CID 20076748.
- ^ Geem, Zong Woo (2006). "Optimal cost design of water distribution networks using harmony search". Engineering Optimization. 38 (3): 259–277. doi:10.1080/03052150500467430. S2CID 18614329.
- ^ Gholizadeh, S.; Barzegar, A. (2013). "Shape optimization of structures for frequency constraints by sequential harmony search algorithm". Engineering Optimization. 45 (6): 627. Bibcode:2013EnOp...45..627G. doi:10.1080/0305215X.2012.704028. S2CID 123589002.
- ^ Wang, Ling; Li, Ling-po (2013). "An effective differential harmony search algorithm for the solving non-convex economic load dispatch problems". International Journal of Electrical Power & Energy Systems. 44: 832–843. doi:10.1016/j.ijepes.2012.08.021.
- ^ Nekooei, Komail; Farsangi, Malihe M.; Nezamabadi-Pour, Hossein; Lee, Kwang Y. (2013). "An Improved Multi-Objective Harmony Search for Optimal Placement of DGs in Distribution Systems". IEEE Transactions on Smart Grid. 4: 557–567. doi:10.1109/TSG.2012.2237420. S2CID 12988437.
- ^ Hadwan, Mohammed; Ayob, Masri; Sabar, Nasser R.; Qu, Roug (2013). "A harmony search algorithm for nurse rostering problems". Information Sciences. 233: 126–140. CiteSeerX 10.1.1.298.6805. doi:10.1016/j.ins.2012.12.025. S2CID 16569649.
- ^ Hoang, Duc Chinh; Yadav, Parikshit; Kumar, Rajesh; Panda, Sanjib Kumar (2014). "Real-Time Implementation of a Harmony Search Algorithm-Based Clustering Protocol for Energy-Efficient Wireless Sensor Networks". IEEE Transactions on Industrial Informatics. 10: 774–783. doi:10.1109/TII.2013.2273739. S2CID 3731612.
- ^ Ren Diao; Qiang Shen (2012). "Feature Selection with Harmony Search". IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics. 42 (6): 1509–23. doi:10.1109/TSMCB.2012.2193613. PMID 22645272. S2CID 206794122.
- ^ Fattahi, Hadi; Gholami, Amin; Amiribakhtiar, Mohammad Sadegh; Moradi, Siyamak (2014). "Estimation of asphaltene precipitation from titration data: A hybrid support vector regression with harmony search". Neural Computing and Applications. 26 (4): 789. doi:10.1007/s00521-014-1766-y. S2CID 16208680.
- ^ "Harmony Search Algorithm". sites.google.com. Retrieved 23 April 2022.
- ^ Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; Del Ser, J.; Bilbao, M.N.; Salcedo-Sanz, S.; Geem, Z.W. (2013). "A survey on applications of the harmony search algorithm". Engineering Applications of Artificial Intelligence. 26 (8): 1818. doi:10.1016/j.engappai.2013.05.008.
- ^ Assif Assad; Deep, Kusum (2016). "Applications of Harmony Search Algorithm in Data Mining: A Survey". Proceedings of Fifth International Conference on Soft Computing for Problem Solving. Advances in Intelligent Systems and Computing. Vol. 437. pp. 863–74. doi:10.1007/978-981-10-0451-3_77. ISBN 978-981-10-0450-6.
- ^ Weyland, Dennis (2015). "A critical analysis of the harmony search algorithm—How not to solve sudoku". Operations Research Perspectives. 2: 97–105. doi:10.1016/j.orp.2015.04.001. hdl:10419/178253.
- ^ Saka, M.; Hasançebi, O.; Seem, Z.W. (2016). "Metaheuristics in structural optimization and discussions on harmony search algorithm". Swarm and Evolutionary Computation. 28: 88–97. doi:10.1016/j.swevo.2016.01.005.
- ^ Karaboga, Dervis (2010). "Artificial bee colony algorithm". Scholarpedia. 5 (3): 6915. Bibcode:2010SchpJ...5.6915K. doi:10.4249/scholarpedia.6915.
- ^ Pham DT, Ghanbarzadeh A, Koc E, Otri S, Rahim S and Zaidi M. The Bees Algorithm. Technical Note, Manufacturing Engineering Centre, Cardiff University, UK, 2005.[page needed]
- ^ Pham, D T; Castellani, M (2009). "The Bees Algorithm: Modelling foraging behaviour to solve continuous optimization problems". Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 223 (12): 2919. doi:10.1243/09544062jmes1494. S2CID 111315200.
- ^ a b Atashpaz-Gargari, Esmaeil; Lucas, Caro (2007). "Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition". 2007 IEEE Congress on Evolutionary Computation. pp. 4661–7. doi:10.1109/CEC.2007.4425083. ISBN 978-1-4244-1339-3. S2CID 2736579.
- ^ a b Nazari-Shirkouhi, S.; Eivazy, H.; Ghodsi, R.; Rezaie, K.; Atashpaz-Gargari, E. (2010). "Solving the integrated product mix-outsourcing problem using the Imperialist Competitive Algorithm". Expert Systems with Applications. 37 (12): 7615. doi:10.1016/j.eswa.2010.04.081. S2CID 17563386.
- ^ Hosseini, Seyedmohsen; Al Khaled, Abdullah (2014). "A survey on the Imperialist Competitive Algorithm metaheuristic: Implementation in engineering domain and directions for future research". Applied Soft Computing. 24: 1078–1094. doi:10.1016/j.asoc.2014.08.024.
- ^ Akl, Selim G.; Calude, Cristian S.; Dinneen, Michael J.; Rozenberg, Grzegorz; Todd Wareham, H. (2007). Unconventional Computation. Lecture Notes in Computer Science. Vol. 4618. arXiv:0711.2964. doi:10.1007/978-3-540-73554-0. ISBN 978-3-540-73553-3.
- ^ Rabanal, Pablo; Rodríguez, Ismael; Rubio, Fernando (2009). "Applying River Formation Dynamics to Solve NP-Complete Problems". Nature-Inspired Algorithms for Optimisation. Studies in Computational Intelligence. Vol. 193. pp. 333–68. doi:10.1007/978-3-642-00267-0_12. ISBN 978-3-642-00266-3.
- ^ Amin, Saman Hameed; Al-Raweshidy, H.S.; Abbas, Rafed Sabbar (2014). "Smart data packet ad hoc routing protocol". Computer Networks. 62: 162–181. doi:10.1016/j.bjp.2013.11.015.
- ^ Redlarski, Grzegorz; Pałkowski, Aleksander; Dąbkowski, Mariusz (2013). "Using River Formation Dynamics Algorithm in Mobile Robot Navigation". Solid State Phenomena. 198: 138–143. doi:10.4028/www.scientific.net/SSP.198.138. S2CID 137020536.
- ^ Rabanal, Pablo; Rodríguez, Ismael; Rubio, Fernando (2017). "Applications of river formation dynamics" (PDF). Journal of Computational Science. 22: 26–35. doi:10.1016/j.jocs.2017.08.002.
- ^ Rashedi, Esmat; Nezamabadi-Pour, Hossein; Saryazdi, Saeid (2009). "GSA: A Gravitational Search Algorithm". Information Sciences. 179 (13): 2232. doi:10.1016/j.ins.2009.03.004.
- ^ Rashedi, Esmat; Nezamabadi-pour, Hossein; Saryazdi, Saeid (2009-06-13). "GSA: A Gravitational Search Algorithm". Information Sciences. Special Section on High Order Fuzzy Sets. 179 (13): 2232–2248. doi:10.1016/j.ins.2009.03.004. ISSN 0020-0255.
- ^ Hassanzadeh, Hamid Reza; Rouhani, Modjtaba (2010). "A Multi-objective Gravitational Search Algorithm". 2010 2nd International Conference on Computational Intelligence, Communication Systems and Networks. pp. 7–12. doi:10.1109/CICSyN.2010.32. ISBN 978-1-4244-7837-8. S2CID 649636.
- ^ Yang, Xin-She (2010). "A New Metaheuristic Bat-Inspired Algorithm". Nature Inspired Cooperative Strategies for Optimization (NICSO 2010). Studies in Computational Intelligence. Vol. 284. pp. 65–74. CiteSeerX 10.1.1.761.2708. doi:10.1007/978-3-642-12538-6_6. ISBN 978-3-642-12537-9. S2CID 14494281.
- ^ Tamura, Kenichi; Yasuda, Keiichiro (2016). "Spiral Optimization Algorithm Using Periodic Descent Directions". SICE Journal of Control, Measurement, and System Integration. 9 (3): 134–43. Bibcode:2016JCMSI...9..134T. doi:10.9746/jcmsi.9.134.
- ^ Rosenberg, Louis (February 12, 2016). "Artificial Swarm Intelligence, a Human-in-the-Loop Approach to A.I." Proceedings of the AAAI Conference on Artificial Intelligence. 30. doi:10.1609/aaai.v30i1.9833. S2CID 8824332.
- ^ Reese, Hope (Jan 22, 2016). "How 'artificial swarm intelligence' uses people to make better predictions than experts".
- ^ Rosenberg, Louis B. (2015). "Human swarming, a real-time method for parallel distributed intelligence". 2015 Swarm/Human Blended Intelligence Workshop (SHBI). pp. 1–7. doi:10.1109/SHBI.2015.7321685. ISBN 978-1-4673-6522-2. S2CID 15166767.
- ^ Cuthbertson, Anthony (10 May 2016). "Artificial intelligence turns $20 into $11,000 in Kentucky Derby bet". Newsweek. Retrieved 23 April 2022.
- ^ Ohlheiser, Abby (2 June 2016). "What happened when an A.I. hive mind answered Reddit's burning politics questions". Washington Post. Retrieved 23 April 2022.
- ^ Huang, Changwu; Li, Yuanxiang; Yao, Xin (2019). "A Survey of Automatic Parameter Tuning Methods for Metaheuristics". IEEE Transactions on Evolutionary Computation. 24 (2): 201–216. doi:10.1109/TEVC.2019.2921598. ISSN 1089-778X.
- ^ Nobile, Marco S.; Cazzaniga, Paolo; Besozzi, Daniela; Colombo, Riccardo; Mauri, Giancarlo; Pasi, Gabriella (2018). "Fuzzy Self-Tuning PSO: A settings-free algorithm for global optimization". Swarm and Evolutionary Computation. 39: 70–85. doi:10.1016/j.swevo.2017.09.001. hdl:10446/106467.
- ^ Zervoudakis, Konstantinos; Tsafarakis, Stelios (2023). "A global optimizer inspired from the survival strategies of flying foxes". Engineering with Computers. 39 (2): 1583–1616. doi:10.1007/s00366-021-01554-w. ISSN 0177-0667.
- ^ a b Alexander Brownlee and John R. Woodward (2015). "Why we fell out of love with algorithms inspired by nature". The Conversation.
- ^ Jerry Swan, Steven Adriaensen, Mohamed Bishr, Edmund K. Burke, John A. Clark, Patrick De Causmaecker, Juanjo Durillo, Kevin Hammond, Emma Hart, Colin G. Johnson, Zoltan A. Kocsis, Ben Kovitz, Krzysztof Krawiec, Simon Martin, J. J. Merelo, Leandro L. Minku, Ender Özcan, Gisele L. Pappa, Erwin Pesch, Pablo García-Sánchez, Andrea Schaerf, Kevin Sim, Jim E. Smith, Thomas Stützle, Stefan Voß, Stefan Wagner, Xin Yao. "A Research Agenda for Metaheuristic Standardization". "Metaphors often inspire new metaheuristics, but without mathematical rigor, it can be hard to tell if a new metaheuristic is really distinct from a familiar one. For example, mathematically, 'Harmony search' turned out to be a simple variant of 'Evolution Strategies' even though the metaphors that inspired them were quite different. Formally describing state, representation, and operators allows genuine novelty to be distinguished from minor variation."
- ^ Sörensen, Kenneth (2015). "Metaheuristics-the metaphor exposed". International Transactions in Operational Research. 22: 3–18. CiteSeerX 10.1.1.470.3422. doi:10.1111/itor.12001. S2CID 14042315.
- ^ Fred Glover and Kenneth Sörensen (ed.). "Metaheuristics". Scholarpedia.
- ^ "Journal of Heuristic Policies on Heuristic Search Research" (PDF). www.springer.com. Archived from the original (PDF) on 9 July 2017.
- ^ "4OR – incl. Option to publish open access". www.springer.com. Retrieved 23 April 2022.
- ^ "ACM Transactions on Evolutionary Learning and Optimization - Author Guidelines". dl.acm.org/. Retrieved 9 April 2024.
- ^ "Evolutionary Computation - Submission Guidelines". direct.mit.edu/evco/. Retrieved 9 April 2024.
References[edit]
- Sörensen, Kenneth; Sevaux, Marc; Glover, Fred (2017-01-16). "A History of Metaheuristics" (PDF). In Martí, Rafael; Panos, Pardalos; Resende, Mauricio (eds.). Handbook of Heuristics. Springer. ISBN 978-3-319-07123-7.
- Sörensen, Kenneth (2015). "Metaheuristics-the metaphor exposed". International Transactions in Operational Research. 22: 3–18. CiteSeerX 10.1.1.470.3422. doi:10.1111/itor.12001. S2CID 14042315.
- Lones, Michael A. (2014). "Metaheuristics in nature-inspired algorithms". Proceedings of the 2014 conference companion on Genetic and evolutionary computation companion - GECCO Comp '14. pp. 1419–22. CiteSeerX 10.1.1.699.1825. doi:10.1145/2598394.2609841. ISBN 9781450328814. S2CID 14997975.
- Fister, Iztok; Yang, Xin-She; Fister, Iztok; Brest, Janez; Fister, Dušan (2013). "A Brief Review of Nature-Inspired Algorithms for Optimization". Elektrotehniški Vestnik. arXiv:1307.4186.
External links[edit]
- Evolutionary Computation Bestiary – a tongue-in-cheek account of all the weird metaphor-based metaheuristics out there in the wide world of academic publishing
- The Science Matrix's List of Metaheuristic[dead link] – a complete list of metaheuristic algorithms filterable by name, author or year, providing a link to main publication of each algorithm

