Saddle-node bifurcation
In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed points (or equilibria) of a dynamical system collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue sky bifurcation in reference to the sudden creation of two fixed points.[1]
If the phase space is one-dimensional, one of the equilibrium points is unstable (the saddle), while the other is stable (the node).
Saddle-node bifurcations may be associated with hysteresis loops and catastrophes.
Normal form[edit]
A typical example of a differential equation with a saddle-node bifurcation is:
Here is the state variable and is the bifurcation parameter.
- If there are two equilibrium points, a stable equilibrium point at and an unstable one at .
- At (the bifurcation point) there is exactly one equilibrium point. At this point the fixed point is no longer hyperbolic. In this case the fixed point is called a saddle-node fixed point.
- If there are no equilibrium points.[2]
In fact, this is a normal form of a saddle-node bifurcation. A scalar differential equation which has a fixed point at for with is locally topologically equivalent to , provided it satisfies and . The first condition is the nondegeneracy condition and the second condition is the transversality condition.[3]
Example in two dimensions[edit]
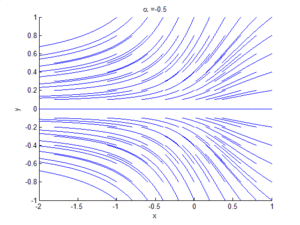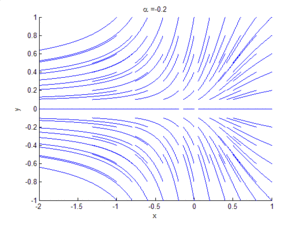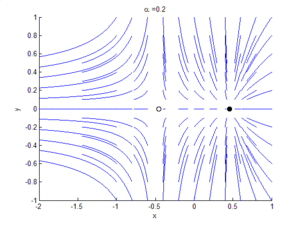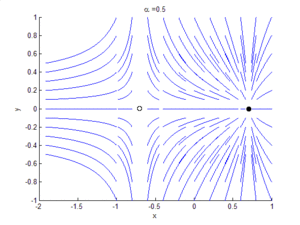
An example of a saddle-node bifurcation in two dimensions occurs in the two-dimensional dynamical system:
As can be seen by the animation obtained by plotting phase portraits by varying the parameter ,
- When is negative, there are no equilibrium points.
- When , there is a saddle-node point.
- When is positive, there are two equilibrium points: that is, one saddle point and one node (either an attractor or a repellor).
Other examples are in modelling biological switches.[4] Recently, it was shown that under certain conditions, the Einstein field equations of General Relativity have the same form as a fold bifurcation.[5] A non-autonomous version of the saddle-node bifurcation (i.e. the parameter is time-dependent) has also been studied.[6]
See also[edit]
Notes[edit]
- ^ Strogatz 1994, p. 47.
- ^ Kuznetsov 1998, pp. 80–81.
- ^ Kuznetsov 1998, Theorems 3.1 and 3.2.
- ^ Chong, Ket Hing; Samarasinghe, Sandhya; Kulasiri, Don; Zheng, Jie (2015). Computational techniques in mathematical modelling of biological switches. 21st International Congress on Modelling and Simulation. hdl:10220/42793.
- ^ Kohli, Ikjyot Singh; Haslam, Michael C (2018). "Einstein's field equations as a fold bifurcation". Journal of Geometry and Physics. 123: 434–7. arXiv:1607.05300. Bibcode:2018JGP...123..434K. doi:10.1016/j.geomphys.2017.10.001. S2CID 119196982.
- ^ Li, Jeremiah H.; Ye, Felix X. -F.; Qian, Hong; Huang, Sui (2019-08-01). "Time-dependent saddle–node bifurcation: Breaking time and the point of no return in a non-autonomous model of critical transitions". Physica D: Nonlinear Phenomena. 395: 7–14. arXiv:1611.09542. Bibcode:2019PhyD..395....7L. doi:10.1016/j.physd.2019.02.005. ISSN 0167-2789. PMC 6836434. PMID 31700198.
References[edit]
- Kuznetsov, Yuri A. (1998). Elements of Applied Bifurcation Theory (Second ed.). Springer. ISBN 0-387-98382-1.
- Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos. Addison Wesley. ISBN 0-201-54344-3.
- Weisstein, Eric W. "Fold Bifurcation". MathWorld.
- Chong, K. H.; Samarasinghe, S.; Kulasiri, D.; Zheng, J. (2015). Computational Techniques in Mathematical Modelling of Biological Switches. In Weber, T., McPhee, M.J. and Anderssen, R.S. (eds) MODSIM2015, 21st International Congress on Modelling and Simulation (MODSIM 2015). Modelling and Simulation Society of Australia and New Zealand, December 2015, pp. 578-584. ISBN 978-0-9872143-5-5.
- Kohli, Ikjyot Singh; Haslam, Michael C. (2018). Einstein Field Equations as a Fold Bifurcation. Journal of Geometry and Physics Volume 123, January 2018, Pages 434-437.


















