Sound

In physics, sound is a vibration that propagates as an acoustic wave through a transmission medium such as a gas, liquid or solid. In human physiology and psychology, sound is the reception of such waves and their perception by the brain.[1] Only acoustic waves that have frequencies lying between about 20 Hz and 20 kHz, the audio frequency range, elicit an auditory percept in humans. In air at atmospheric pressure, these represent sound waves with wavelengths of 17 meters (56 ft) to 1.7 centimeters (0.67 in). Sound waves above 20 kHz are known as ultrasound and are not audible to humans. Sound waves below 20 Hz are known as infrasound. Different animal species have varying hearing ranges.
Definition
Sound is defined as "(a) Oscillation in pressure, stress, particle displacement, particle velocity, etc., propagated in a medium with internal forces (e.g., elastic or viscous), or the superposition of such propagated oscillation. (b) Auditory sensation evoked by the oscillation described in (a)."[2] Sound can be viewed as a wave motion in air or other elastic media. In this case, sound is a stimulus. Sound can also be viewed as an excitation of the hearing mechanism that results in the perception of sound. In this case, sound is a sensation.
Acoustics
Acoustics is the interdisciplinary science that deals with the study of mechanical waves in gasses, liquids, and solids including vibration, sound, ultrasound, and infrasound. A scientist who works in the field of acoustics is an acoustician, while someone working in the field of acoustical engineering may be called an acoustical engineer.[3] An audio engineer, on the other hand, is concerned with the recording, manipulation, mixing, and reproduction of sound.
Applications of acoustics are found in almost all aspects of modern society, subdisciplines include aeroacoustics, audio signal processing, architectural acoustics, bioacoustics, electro-acoustics, environmental noise, musical acoustics, noise control, psychoacoustics, speech, ultrasound, underwater acoustics, and vibration.[4]
Physics
Sound can propagate through a medium such as air, water and solids as longitudinal waves and also as a transverse wave in solids. The sound waves are generated by a sound source, such as the vibrating diaphragm of a stereo speaker. The sound source creates vibrations in the surrounding medium. As the source continues to vibrate the medium, the vibrations propagate away from the source at the speed of sound, thus forming the sound wave. At a fixed distance from the source, the pressure, velocity, and displacement of the medium vary in time. At an instant in time, the pressure, velocity, and displacement vary in space. The particles of the medium do not travel with the sound wave. This is intuitively obvious for a solid, and the same is true for liquids and gases (that is, the vibrations of particles in the gas or liquid transport the vibrations, while the average position of the particles over time does not change). During propagation, waves can be reflected, refracted, or attenuated by the medium.[5]
The behavior of sound propagation is generally affected by three things:
- A complex relationship between the density and pressure of the medium. This relationship, affected by temperature, determines the speed of sound within the medium.
- Motion of the medium itself. If the medium is moving, this movement may increase or decrease the absolute speed of the sound wave depending on the direction of the movement. For example, sound moving through wind will have its speed of propagation increased by the speed of the wind if the sound and wind are moving in the same direction. If the sound and wind are moving in opposite directions, the speed of the sound wave will be decreased by the speed of the wind.
- The viscosity of the medium. Medium viscosity determines the rate at which sound is attenuated. For many media, such as air or water, attenuation due to viscosity is negligible.
When sound is moving through a medium that does not have constant physical properties, it may be refracted (either dispersed or focused).[5]

The mechanical vibrations that can be interpreted as sound can travel through all forms of matter: gases, liquids, solids, and plasmas. The matter that supports the sound is called the medium. Sound cannot travel through a vacuum.[6][7]
Studies has shown that sound waves are able to carry a tiny amount of mass and is surrounded by a weak gravitational field.[8]
Waves
Sound is transmitted through gases, plasma, and liquids as longitudinal waves, also called compression waves. It requires a medium to propagate. Through solids, however, it can be transmitted as both longitudinal waves and transverse waves. Longitudinal sound waves are waves of alternating pressure deviations from the equilibrium pressure, causing local regions of compression and rarefaction, while transverse waves (in solids) are waves of alternating shear stress at right angle to the direction of propagation.
Sound waves may be viewed using parabolic mirrors and objects that produce sound.[9]
The energy carried by an oscillating sound wave converts back and forth between the potential energy of the extra compression (in case of longitudinal waves) or lateral displacement strain (in case of transverse waves) of the matter, and the kinetic energy of the displacement velocity of particles of the medium.

Although there are many complexities relating to the transmission of sounds, at the point of reception (i.e. the ears), sound is readily dividable into two simple elements: pressure and time. These fundamental elements form the basis of all sound waves. They can be used to describe, in absolute terms, every sound we hear.
In order to understand the sound more fully, a complex wave such as the one shown in a blue background on the right of this text, is usually separated into its component parts, which are a combination of various sound wave frequencies (and noise).[10][11][12]
Sound waves are often simplified to a description in terms of sinusoidal plane waves, which are characterized by these generic properties:
- Frequency, or its inverse, wavelength
- Amplitude, sound pressure or Intensity
- Speed of sound
- Direction
Sound that is perceptible by humans has frequencies from about 20 Hz to 20,000 Hz. In air at standard temperature and pressure, the corresponding wavelengths of sound waves range from 17 m (56 ft) to 17 mm (0.67 in). Sometimes speed and direction are combined as a velocity vector; wave number and direction are combined as a wave vector.
Transverse waves, also known as shear waves, have the additional property, polarization, which is not a characteristic of longitudinal sound waves.[13]
Speed

The speed of sound depends on the medium the waves pass through, and is a fundamental property of the material. The first significant effort towards measurement of the speed of sound was made by Isaac Newton. He believed the speed of sound in a particular substance was equal to the square root of the pressure acting on it divided by its density:
This was later proven wrong and the French mathematician Laplace corrected the formula by deducing that the phenomenon of sound travelling is not isothermal, as believed by Newton, but adiabatic. He added another factor to the equation—gamma—and multiplied by , thus coming up with the equation . Since , the final equation came up to be , which is also known as the Newton–Laplace equation. In this equation, K is the elastic bulk modulus, c is the velocity of sound, and is the density. Thus, the speed of sound is proportional to the square root of the ratio of the bulk modulus of the medium to its density.
Those physical properties and the speed of sound change with ambient conditions. For example, the speed of sound in gases depends on temperature. In 20 °C (68 °F) air at sea level, the speed of sound is approximately 343 m/s (1,230 km/h; 767 mph) using the formula v [m/s] = 331 + 0.6 T [°C]. The speed of sound is also slightly sensitive, being subject to a second-order anharmonic effect, to the sound amplitude, which means there are non-linear propagation effects, such as the production of harmonics and mixed tones not present in the original sound (see parametric array). If relativistic effects are important, the speed of sound is calculated from the relativistic Euler equations.
In fresh water the speed of sound is approximately 1,482 m/s (5,335 km/h; 3,315 mph). In steel, the speed of sound is about 5,960 m/s (21,460 km/h; 13,330 mph). Sound moves the fastest in solid atomic hydrogen at about 36,000 m/s (129,600 km/h; 80,530 mph).[15][16]
Sound pressure level
| Sound measurements | |
|---|---|
Characteristic | Symbols |
| Sound pressure | p, SPL, LPA |
| Particle velocity | v, SVL |
| Particle displacement | δ |
| Sound intensity | I, SIL |
| Sound power | P, SWL, LWA |
| Sound energy | W |
| Sound energy density | w |
| Sound exposure | E, SEL |
| Acoustic impedance | Z |
| Audio frequency | AF |
| Transmission loss | TL |
Sound pressure is the difference, in a given medium, between average local pressure and the pressure in the sound wave. A square of this difference (i.e., a square of the deviation from the equilibrium pressure) is usually averaged over time and/or space, and a square root of this average provides a root mean square (RMS) value. For example, 1 Pa RMS sound pressure (94 dBSPL) in atmospheric air implies that the actual pressure in the sound wave oscillates between (1 atm Pa) and (1 atm Pa), that is between 101323.6 and 101326.4 Pa. As the human ear can detect sounds with a wide range of amplitudes, sound pressure is often measured as a level on a logarithmic decibel scale. The sound pressure level (SPL) or Lp is defined as
- where p is the root-mean-square sound pressure and is a reference sound pressure. Commonly used reference sound pressures, defined in the standard ANSI S1.1-1994, are 20 µPa in air and 1 µPa in water. Without a specified reference sound pressure, a value expressed in decibels cannot represent a sound pressure level.
Since the human ear does not have a flat spectral response, sound pressures are often frequency weighted so that the measured level matches perceived levels more closely. The International Electrotechnical Commission (IEC) has defined several weighting schemes. A-weighting attempts to match the response of the human ear to noise and A-weighted sound pressure levels are labeled dBA. C-weighting is used to measure peak levels.
Perception
A distinct use of the term sound from its use in physics is that in physiology and psychology, where the term refers to the subject of perception by the brain. The field of psychoacoustics is dedicated to such studies. Webster's dictionary defined sound as: "1. The sensation of hearing, that which is heard; specif.: a. Psychophysics. Sensation due to stimulation of the auditory nerves and auditory centers of the brain, usually by vibrations transmitted in a material medium, commonly air, affecting the organ of hearing. b. Physics. Vibrational energy which occasions such a sensation. Sound is propagated by progressive longitudinal vibratory disturbances (sound waves)."[17] This means that the correct response to the question: "if a tree falls in the forest with no one to hear it fall, does it make a sound?" is "yes", and "no", dependent on whether being answered using the physical, or the psychophysical definition, respectively.
The physical reception of sound in any hearing organism is limited to a range of frequencies. Humans normally hear sound frequencies between approximately 20 Hz and 20,000 Hz (20 kHz),[18]: 382 The upper limit decreases with age.[18]: 249 Sometimes sound refers to only those vibrations with frequencies that are within the hearing range for humans[19] or sometimes it relates to a particular animal. Other species have different ranges of hearing. For example, dogs can perceive vibrations higher than 20 kHz.
As a signal perceived by one of the major senses, sound is used by many species for detecting danger, navigation, predation, and communication. Earth's atmosphere, water, and virtually any physical phenomenon, such as fire, rain, wind, surf, or earthquake, produces (and is characterized by) its unique sounds. Many species, such as frogs, birds, marine and terrestrial mammals, have also developed special organs to produce sound. In some species, these produce song and speech. Furthermore, humans have developed culture and technology (such as music, telephone and radio) that allows them to generate, record, transmit, and broadcast sound.
Noise is a term often used to refer to an unwanted sound. In science and engineering, noise is an undesirable component that obscures a wanted signal. However, in sound perception it can often be used to identify the source of a sound and is an important component of timbre perception (see below).
Soundscape is the component of the acoustic environment that can be perceived by humans. The acoustic environment is the combination of all sounds (whether audible to humans or not) within a given area as modified by the environment and understood by people, in context of the surrounding environment.
There are, historically, six experimentally separable ways in which sound waves are analysed. They are: pitch, duration, loudness, timbre, sonic texture and spatial location.[20] Some of these terms have a standardised definition (for instance in the ANSI Acoustical Terminology ANSI/ASA S1.1-2013). More recent approaches have also considered temporal envelope and temporal fine structure as perceptually relevant analyses.[21][22][23]
Pitch
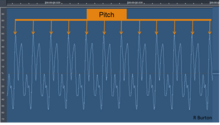
Pitch is perceived as how "low" or "high" a sound is and represents the cyclic, repetitive nature of the vibrations that make up sound. For simple sounds, pitch relates to the frequency of the slowest vibration in the sound (called the fundamental harmonic). In the case of complex sounds, pitch perception can vary. Sometimes individuals identify different pitches for the same sound, based on their personal experience of particular sound patterns. Selection of a particular pitch is determined by pre-conscious examination of vibrations, including their frequencies and the balance between them. Specific attention is given to recognising potential harmonics.[24][25] Every sound is placed on a pitch continuum from low to high. For example: white noise (random noise spread evenly across all frequencies) sounds higher in pitch than pink noise (random noise spread evenly across octaves) as white noise has more high frequency content. Figure 1 shows an example of pitch recognition. During the listening process, each sound is analysed for a repeating pattern (See Figure 1: orange arrows) and the results forwarded to the auditory cortex as a single pitch of a certain height (octave) and chroma (note name).
Duration

Duration is perceived as how "long" or "short" a sound is and relates to onset and offset signals created by nerve responses to sounds. The duration of a sound usually lasts from the time the sound is first noticed until the sound is identified as having changed or ceased.[26] Sometimes this is not directly related to the physical duration of a sound. For example; in a noisy environment, gapped sounds (sounds that stop and start) can sound as if they are continuous because the offset messages are missed owing to disruptions from noises in the same general bandwidth.[27] This can be of great benefit in understanding distorted messages such as radio signals that suffer from interference, as (owing to this effect) the message is heard as if it was continuous. Figure 2 gives an example of duration identification. When a new sound is noticed (see Figure 2, Green arrows), a sound onset message is sent to the auditory cortex. When the repeating pattern is missed, a sound offset messages is sent.
Loudness

Loudness is perceived as how "loud" or "soft" a sound is and relates to the totalled number of auditory nerve stimulations over short cyclic time periods, most likely over the duration of theta wave cycles.[28][29][30] This means that at short durations, a very short sound can sound softer than a longer sound even though they are presented at the same intensity level. Past around 200 ms this is no longer the case and the duration of the sound no longer affects the apparent loudness of the sound. Figure 3 gives an impression of how loudness information is summed over a period of about 200 ms before being sent to the auditory cortex. Louder signals create a greater 'push' on the Basilar membrane and thus stimulate more nerves, creating a stronger loudness signal. A more complex signal also creates more nerve firings and so sounds louder (for the same wave amplitude) than a simpler sound, such as a sine wave.
Timbre
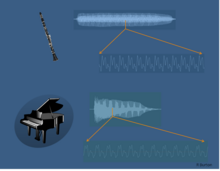
Timbre is perceived as the quality of different sounds (e.g. the thud of a fallen rock, the whir of a drill, the tone of a musical instrument or the quality of a voice) and represents the pre-conscious allocation of a sonic identity to a sound (e.g. "it's an oboe!"). This identity is based on information gained from frequency transients, noisiness, unsteadiness, perceived pitch and the spread and intensity of overtones in the sound over an extended time frame.[10][11][12] The way a sound changes over time (see figure 4) provides most of the information for timbre identification. Even though a small section of the wave form from each instrument looks very similar (see the expanded sections indicated by the orange arrows in figure 4), differences in changes over time between the clarinet and the piano are evident in both loudness and harmonic content. Less noticeable are the different noises heard, such as air hisses for the clarinet and hammer strikes for the piano.
Texture
Sonic texture relates to the number of sound sources and the interaction between them.[31][32] The word texture, in this context, relates to the cognitive separation of auditory objects.[33] In music, texture is often referred to as the difference between unison, polyphony and homophony, but it can also relate (for example) to a busy cafe; a sound which might be referred to as cacophony.
Spatial location
Spatial location represents the cognitive placement of a sound in an environmental context; including the placement of a sound on both the horizontal and vertical plane, the distance from the sound source and the characteristics of the sonic environment.[33][34] In a thick texture, it is possible to identify multiple sound sources using a combination of spatial location and timbre identification.
Frequency
Ultrasound

Ultrasound is sound waves with frequencies higher than 20,000 Hz. Ultrasound is not different from audible sound in its physical properties, but cannot be heard by humans. Ultrasound devices operate with frequencies from 20 kHz up to several gigahertz.
Medical ultrasound is commonly used for diagnostics and treatment.
Infrasound
Infrasound is sound waves with frequencies lower than 20 Hz. Although sounds of such low frequency are too low for humans to hear as a pitch, these sound are heard as discrete pulses (like the 'popping' sound of an idling motorcycle). Whales, elephants and other animals can detect infrasound and use it to communicate. It can be used to detect volcanic eruptions and is used in some types of music.[35]
See also
- Sound sources
- Sound measurement
- Acoustic impedance
- Acoustic velocity
- Characteristic impedance
- Mel scale
- Particle acceleration
- Particle amplitude
- Particle displacement
- Particle velocity
- Sound energy flux
- Sound impedance
- Sound intensity level
- Sound power
- Sound power level
- Units
- General
- Acoustic theory
- Beat
- Doppler effect
- Echo
- Infrasound — sound at extremely low frequencies
- List of unexplained sounds
- Musical tone
- Resonance
- Reverberation
- Sonic weaponry
- Sound synthesis
- Soundproofing
- Structural acoustics
References
- ^ Fundamentals of Telephone Communication Systems. Western Electrical Company. 1969. p. 2.1.
- ^ ANSI/ASA S1.1-2013
- ^ ANSI S1.1-1994. American National Standard: Acoustic Terminology. Sec 3.03.
- ^ Acoustical Society of America. "PACS 2010 Regular Edition—Acoustics Appendix". Archived from the original on 14 May 2013. Retrieved 22 May 2013.
- ^ a b "The Propagation of sound". Archived from the original on 30 April 2015. Retrieved 26 June 2015.
- ^ Is there sound in space? Archived 2017-10-16 at the Wayback Machine Northwestern University.
- ^ Can you hear sounds in space? (Beginner) Archived 2017-06-18 at the Wayback Machine. Cornell University.
- ^ Beyond cloning: Harnessing the power of virtual quantum broadcasting
- ^ "What Does Sound Look Like?". NPR. YouTube. Archived from the original on 10 April 2014. Retrieved 9 April 2014.
- ^ a b Handel, S. (1995). Timbre perception and auditory object identification Archived 2020-01-10 at the Wayback Machine. Hearing, 425–461.
- ^ a b Kendall, R.A. (1986). The role of acoustic signal partitions in listener categorization of musical phrases. Music Perception, 185–213.
- ^ a b Matthews, M. (1999). Introduction to timbre. In P.R. Cook (Ed.), Music, cognition, and computerized sound: An introduction to psychoacoustic (pp. 79–88). Cambridge, Massachusetts: The MIT press.
- ^ Breinig, Marianne. "Polarization". Elements of Physics II. The University of Tennessee, Department of Physics and Astronomy. Retrieved 4 March 2024.
- ^ Nemiroff, R.; Bonnell, J., eds. (19 August 2007). "A Sonic Boom". Astronomy Picture of the Day. NASA. Retrieved 26 June 2015.
- ^ "Scientists find upper limit for the speed of sound". Archived from the original on 2020-10-09. Retrieved 2020-10-09.
- ^ Trachenko, K.; Monserrat, B.; Pickard, C. J.; Brazhkin, V. V. (2020). "Speed of sound from fundamental physical constants". Science Advances. 6 (41): eabc8662. arXiv:2004.04818. Bibcode:2020SciA....6.8662T. doi:10.1126/sciadv.abc8662. PMC 7546695. PMID 33036979.
- ^ Webster, Noah (1936). Sound. In Webster's Collegiate Dictionary (Fifth ed.). Cambridge, Mass.: The Riverside Press. pp. 950–951.
- ^ a b Olson, Harry F. Autor (1967). Music, Physics and Engineering. Dover Publications. p. 249. ISBN 9780486217697.
- ^ "The American Heritage Dictionary of the English Language" (Fourth ed.). Houghton Mifflin Company. 2000. Archived from the original on June 25, 2008. Retrieved May 20, 2010.
- ^ Burton, R.L. (2015). The elements of music: what are they, and who cares? Archived 2020-05-10 at the Wayback Machine In J. Rosevear & S. Harding. (Eds.), ASME XXth National Conference proceedings. Paper presented at: Music: Educating for life: ASME XXth National Conference (pp. 22–28), Parkville, Victoria: The Australian Society for Music Education Inc.
- ^ Viemeister, Neal F.; Plack, Christopher J. (1993), "Time Analysis", Springer Handbook of Auditory Research, Springer New York, pp. 116–154, doi:10.1007/978-1-4612-2728-1_4, ISBN 9781461276449
- ^ Rosen, Stuart (1992-06-29). "Temporal information in speech: acoustic, auditory and linguistic aspects". Phil. Trans. R. Soc. Lond. B. 336 (1278): 367–373. Bibcode:1992RSPTB.336..367R. doi:10.1098/rstb.1992.0070. ISSN 0962-8436. PMID 1354376.
- ^ Moore, Brian C.J. (2008-10-15). "The Role of Temporal Fine Structure Processing in Pitch Perception, Masking, and Speech Perception for Normal-Hearing and Hearing-Impaired People". Journal of the Association for Research in Otolaryngology. 9 (4): 399–406. doi:10.1007/s10162-008-0143-x. ISSN 1525-3961. PMC 2580810. PMID 18855069.
- ^ De Cheveigne, A. (2005). Pitch perception models. Pitch, 169-233.
- ^ Krumbholz, K.; Patterson, R.; Seither-Preisler, A.; Lammertmann, C.; Lütkenhöner, B. (2003). "Neuromagnetic evidence for a pitch processing center in Heschl's gyrus". Cerebral Cortex. 13 (7): 765–772. doi:10.1093/cercor/13.7.765. PMID 12816892.
- ^ Jones, S.; Longe, O.; Pato, M.V. (1998). "Auditory evoked potentials to abrupt pitch and timbre change of complex tones: electrophysiological evidence of streaming?". Electroencephalography and Clinical Neurophysiology. 108 (2): 131–142. doi:10.1016/s0168-5597(97)00077-4. PMID 9566626.
- ^ Nishihara, M.; Inui, K.; Morita, T.; Kodaira, M.; Mochizuki, H.; Otsuru, N.; Kakigi, R. (2014). "Echoic memory: Investigation of its temporal resolution by auditory offset cortical responses". PLOS ONE. 9 (8): e106553. Bibcode:2014PLoSO...9j6553N. doi:10.1371/journal.pone.0106553. PMC 4149571. PMID 25170608.
- ^ Corwin, J. (2009), The auditory system (PDF), archived (PDF) from the original on 2013-06-28, retrieved 2013-04-06
- ^ Massaro, D.W. (1972). "Preperceptual images, processing time, and perceptual units in auditory perception". Psychological Review. 79 (2): 124–145. CiteSeerX 10.1.1.468.6614. doi:10.1037/h0032264. PMID 5024158.
- ^ Zwislocki, J.J. (1969). "Temporal summation of loudness: an analysis". The Journal of the Acoustical Society of America. 46 (2B): 431–441. Bibcode:1969ASAJ...46..431Z. doi:10.1121/1.1911708. PMID 5804115.
- ^ Cohen, D.; Dubnov, S. (1997), "Gestalt phenomena in musical texture", Journal of New Music Research, 26 (4): 277–314, doi:10.1080/09298219708570732, archived (PDF) from the original on 2015-11-21, retrieved 2015-11-19
- ^ Kamien, R. (1980). Music: an appreciation. New York: McGraw-Hill. p. 62
- ^ a b Cariani, Peter; Micheyl, Christophe (2012). "Toward a Theory of Information Processing in Auditory Cortex". The Human Auditory Cortex. Springer Handbook of Auditory Research. Vol. 43. pp. 351–390. doi:10.1007/978-1-4614-2314-0_13. ISBN 978-1-4614-2313-3.
- ^ Levitin, D.J. (1999). Memory for musical attributes. In P.R. Cook (Ed.), Music, cognition, and computerized sound: An introduction to psychoacoustics (pp. 105–127). Cambridge, Massachusetts: The MIT press.
- ^ Leventhall, Geoff (2007-01-01). "What is infrasound?". Progress in Biophysics and Molecular Biology. Effects of ultrasound and infrasound relevant to human health. 93 (1): 130–137. doi:10.1016/j.pbiomolbio.2006.07.006. ISSN 0079-6107. PMID 16934315.
External links
- Eric Mack (20 May 2019). "Stanford scientists created a sound so loud it instantly boils water". CNET.
- Sounds Amazing; a KS3/4 learning resource for sound and waves (uses Flash) Archived 2012-03-13 at the Wayback Machine
- HyperPhysics: Sound and Hearing
- Introduction to the Physics of Sound
- Hearing curves and on-line hearing test
- Audio for the 21st Century Archived 2009-01-23 at the Wayback Machine
- Conversion of sound units and levels
- Sound calculations
- Audio Check: a free collection of audio tests and test tones playable on-line
- More Sounds Amazing; a sixth-form learning resource about sound waves















