Wikipedia talk:WikiProject Mathematics/Archive/2008/Nov
groups "similar" to Emmy Noether?[edit]
I added a request to put the recently featured article about groups on the main page. This system is a bit complicated, and the article being showcased probably depends on whether groups are "similar" to Emmy Noether, which was displayed on the main page some weeks ago. If you are interested in having a mathematics article showcased (and not the (n+1)st video game), please join in the discussion over there. Jakob.scholbach (talk) 17:34, 26 October 2008 (UTC)
- I would hope that we have a good chance, mathematics FA's do seem to have a better than average chance of getting to the main page. --Salix (talk): 23:06, 26 October 2008 (UTC)
- I hoped so, too, especially in view of the support uttered by many (thank you) and by the "rules" that are set up. But disappointingly the authorities chose something else, without much ado. It'd be interesting to know what it needs to get displayed at main page other than an accessible, well-written article, and community support. Perhaps a Futurama episode in the application section:)? Kafkaesque. Jakob.scholbach (talk) 22:43, 28 October 2008 (UTC)
- Actually, after reading User:Raul654/Featured article thoughts I think it makes sense. While the "similarity" argument was of course nonsense, I think the article is at most borderline appropriate for the main page, since it is too abstract for most readers. With some patience, the article will eventually get there: see Raul's "resource starvation" remark. But the "underrepresented" credits are not for this type of mathematics article; they are for those with appeal to the layman. Short and somewhat imprecise version: We are much more likely to read about Emmy Noether in Time Magazine than about groups, and therefore Emmy Noether was featured faster. It was a journalistic decision not to feature the article now, and it's a wiki politics decision to make sure that an article of this kind will be featured eventually. --Hans Adler (talk) 23:31, 28 October 2008 (UTC)
- Hm. I won't argue with Raul (and even less so with you, obviously), but it strikes me as very non-wiki-ish to have a process that tries to weigh advantages or disadvantages of some article being displayed or not, and then have one person override the result of that. If it is "borderline", it would/could/should have come to day at the discussion (which it did not). I also don't get your point "it will shown eventually". If it is worth showing it, it can be shown now (if somebody "applies" for it), if not, it should never be featured. (Btw, due to the number of featured articles, for numerical reasons there will be articles that are never shown [if new FA's come in as they do now]). Finally, you refer to the abstraction of the article. I agree it is not what many readers will (want to) read daily, but unless my vision is completely biased, it is something which can be appealing to a layman. (I did get positive response in this respect from lay readers at FAC). Indeed it was one of the main concerns in the later stages of the article development and in particular the FAC process to make it accessible, which, I believe, it is, to the amount that can be expected. If we only feature articles that are understandable/"appealing" to the last line for everybody, isn't that systemically biased? Jakob.scholbach (talk) 23:49, 28 October 2008 (UTC)
- Actually, after reading User:Raul654/Featured article thoughts I think it makes sense. While the "similarity" argument was of course nonsense, I think the article is at most borderline appropriate for the main page, since it is too abstract for most readers. With some patience, the article will eventually get there: see Raul's "resource starvation" remark. But the "underrepresented" credits are not for this type of mathematics article; they are for those with appeal to the layman. Short and somewhat imprecise version: We are much more likely to read about Emmy Noether in Time Magazine than about groups, and therefore Emmy Noether was featured faster. It was a journalistic decision not to feature the article now, and it's a wiki politics decision to make sure that an article of this kind will be featured eventually. --Hans Adler (talk) 23:31, 28 October 2008 (UTC)
- I hoped so, too, especially in view of the support uttered by many (thank you) and by the "rules" that are set up. But disappointingly the authorities chose something else, without much ado. It'd be interesting to know what it needs to get displayed at main page other than an accessible, well-written article, and community support. Perhaps a Futurama episode in the application section:)? Kafkaesque. Jakob.scholbach (talk) 22:43, 28 October 2008 (UTC)
- Seems like we made a couple of tactical errors. Nominating it too quickly after Noether and choosing the 29th rather than a later date which may have given it more time to gain Raul's attention. You live and learn. I still think there is a chance it will appear at Raul's discretion. --Salix (talk): 08:40, 29 October 2008 (UTC)
Into the memory hole?[edit]
So what happened to this discussion? It is evident from the queue that the article will not appear on October 29th, that date that was proposed, but what decision was made ought to be available somewhere. Maybe with some archive of the discussion. Do things like that exist, or does the whole thing vanish from all memory? Michael Hardy (talk) 01:22, 29 October 2008 (UTC)
- ...in fact, I now see that in the time zone used by Wikipedia, it's already October 29th. Michael Hardy (talk) 01:23, 29 October 2008 (UTC)
- There does not seem to be an archive of discussions or a documentation why or how the chosen page was effectively chosen (Raul543's documentation alluded to above is little helpful in this respect -- it roughly says: "in the end, the decision is mine, I carry the burden, I have some pages I will never show, but won't tell which, but there are only a few of them"). What decision is taken is shown at Wikipedia:Today's featured article/October 2008. The relevant edit at the request page reads October 29 scheduled; one slot open. Jakob.scholbach (talk) 07:47, 29 October 2008 (UTC)
Displayed Nov. 5[edit]
Somehow, it did get selected quite soon (so, much ado about nothing from my part...), namely tomorrow, November 5. Perhaps people around can have an watching eye on it during that day. Jakob.scholbach (talk) 07:52, 4 November 2008 (UTC)
Dividing by zero - is it valid ?[edit]
Suppose ab=cd, suppose you let a=0 and c=0. Can you then write b/c = d/a ? Can you further say this is valid for all values of a and c ?
User:Bakken is claiming you can say these things because they are true in the limit.
See here: Talk:Lorentz transformation#There is nothing wrong in dividing by zero. Delaszk (talk) 17:55, 3 November 2008 (UTC)
- If you're working in the Real projective line, that's fine. I'm not sure if the variables in question should be considered to be projective or not. --Tango (talk) 18:17, 3 November 2008 (UTC)
You are assuming that ab = cd. If a = 0 and c = 0 then b/c and d/a are not well defined. It is clearly true that if ab = cd then b/c = d/a provided that b/c and d/a are well defined, i.e. ac ≠ 0. Whenever we divide by zero we get a contradiction. Consider the famous example. Assume that x = y then after multiplying through by x we get x2 = xy. Subtracting y2 from both sides gives x2 - y2 = xy - y2 . Which, after factorisation gives (x + y)(x - y) = y(x - y). Dividing through by x - y gives x + y = y. Assuming that x = y gives 2x = x, and finally dividing through by x gives 2 = 1. Clearly 2 ≠ 1, and so we have a contradiction. The contradiction came from dividing through by x - y and then assuming that x = y, i.e. dividing through by zero. I don't think that projective space is involved here. If it were to be, and the person posing the question knew that it was, then the question wouldn't be posed in the first place. Be careful of limits. Limits and equalities are not the same thing. Δεκλαν Δαφισ (talk) 23:07, 3 November 2008 (UTC)
- Let me try to explain my point again. A genuine singularity in a physical theory has a deep physical meaning to it. You cannot avoid a genuine singularity in a physical system by mathematical transformations. And then there are apparent singularities, due to e.g. an unfortunate choice of coordinates, which can be trivially avoided by "identical" mathematical transformations. These singularities have no deep physics associated with them. Bakken (talk) 13:34, 4 November 2008 (UTC)
- Now, just because one has divided the equation by does not mean that the theory suddenly became singular at . If the theory is well behaving at it is well behaving no matter how you write your equation, , or , or . The theory does not change by a iota. Bakken (talk) 13:34, 4 November 2008 (UTC)
- For Lorentz transformation there is obviously no singularity at , but there is a genuine singularity at which e.g. prevents massive bodies to achieve the speed of light. Bakken (talk) 13:34, 4 November 2008 (UTC)
- Suppose you know some function which is analytic everywhere, except for some points where it has poles. Then apparently you also know the function : you know where it has zeros, where it has poles, you know everything about it, you can calculate it everywhere (except for poles, obviously, but you can calculate the residue, if you want). Thus for all practical purposes and contain the same information, no more, no less -- just the same information. Claiming that by inverting an equation you can get some new physics is something I do not believe. There are no wonders in this world. Bakken (talk) 13:34, 4 November 2008 (UTC)
- however, if you believe that the case has to be considered separately, just do it, consider it separately. But we both know, that there is nothing interesting in this case, it is simply an identical transformation. You can just as well consider the case . Indeed, if somebody somewhere should divide our equation by ... :) (Bakken (talk) 13:34, 4 November 2008 (UTC)).
- I may be in error to say that the derivation as done in that article automatically implies a finite c.
- The question about dividing by zero is however another matter. I inverted the equation to avoid dividing by zero. My argument about finite c stemmed from reading the New Scientist article which said that rotations imply special relativity including a finite c. It was upon reading the article on Lorentz transformations that I thought that the Group postulate derivation must be the thing that the New Scientist article was referring to. Upon using the article's talk page to discuss the inevitabilty (or so I thought) of a finite c, it became apparent that the derivation, as given at the time, involved dividing by zero which I didn't like so I changed it.
- Physically speaking the expression : may be well behaved, but mathematically speaking I would say you can't use this expression if v=0. You say watch out if someone else divides by something else e.g. (v-c/2) but we had to divide by v to show that the expression gives an equality for arbitrary v and is therefore a constant. We needed to divide by v, that was unavoidable, and only possible for nonzero v. Delaszk (talk) 14:50, 4 November 2008 (UTC)
- I take your point that a function that approaches 0/0 can be considered continuous at zero by defining its limit point, but if we include k=lim v to 0 in the definition of k, then the calculations to determine an expression for gamma don't hold. Also delta must be on the numerator. If delta is put on the denominator as it originally appeared in the article, then for delta=0 and a nonzero numerator you would have , and multiplying both sides by delta would give which is a contradiction as the numerator was assumed to be nonzero. I am sure all this has already occurred to you but I am going through the process of writing this just to get everything clear in my mind.Delaszk (talk) 19:30, 5 November 2008 (UTC)
Bakken, you say that "You cannot avoid a genuine singularity in a physical system by mathematical transformations." What about the simplest case of the the transformation T(f)(x) := exp(f(x)). Let the function f be given by f(x) := -1/x2. It follows that the transformation of f is smooth and well defined for all x; T(f)(x) has no singularity at all, but f had an honest singularity that can not be removed by any change of coordinates. Δεκλαν Δαφισ (talk) 10:59, 5 November 2008 (UTC)
One Billion Silhouettes Project for deletion[edit]
A web site about tangrams; sorry if it's off-topic, but the article makes a lot of references to math software. VG ☎ 02:28, 6 November 2008 (UTC)
Vector Resolute vs. Vector Projection.[edit]
I recently came across the article Vector resolute, which is also known as vector projection. I had not heard of this terminology before. Googling the term "vector resolute" turns up about 709 results, and the term "vector projection" turns up about 13,000. I would like to change the article from vector resolute to vector projection, as I see it as the more common term, and move the links so that it points the other way. I cannot decide if this would be inappropriate behavior, so I thought I would ask first. Thenub314 (talk) 07:39, 6 November 2008 (UTC)
- Also I had not heard it. Boris Tsirelson (talk) 11:00, 6 November 2008 (UTC)
OK, I've moved it, and I've fixed the link from template:linear algebra. If you go to vector projection and click on "what links here", you may find many links to the redirect, but most of those will be shown as direct links to vector projection after my edit to the template propogates (if I'm right in guessing that most links to that article result from the template). In 24 hours or so, if you click on "what links here" again, you'll see the actual links to the new redirect page, and then those can be fixed. Michael Hardy (talk) 19:12, 6 November 2008 (UTC)
{{maths rating}}[edit]
This template should probably be updated to include the full range of quality and importance categories. For example List of International Mathematical Olympiads is a featured list but the FL link on Talk:List of International Mathematical Olympiads is currently was red. MSGJ 14:09, 6 November 2008 (UTC)
- Just updated the template. Maybe it was just a typo? MSGJ 14:11, 6 November 2008 (UTC)
Groups to be a main-page featured article, but there's a glitch[edit]
It now appears that group (mathematics) will be "Today's Featured Article" on the main page very soon (tomorrow?).
But there's a glitch: The image of Rubik's Cube featured prominently right at the top of the article is proposed for deletion. The argument is that it's a copyrighted work and therefore any photograph of it is a "derivative work". And people who are not aware of the relevant facts or of copyright law are participating in the discussion, urging deletion. The discussion is [here]. Michael Hardy (talk) 16:45, 4 November 2008 (UTC)
- The image issue has been resolved by choosing another image (
 ). While I like the Rubik image better, I think this one is OK, too. The page is featured tomorrow, Nov. 5. Jakob.scholbach (talk) 16:48, 4 November 2008 (UTC)
). While I like the Rubik image better, I think this one is OK, too. The page is featured tomorrow, Nov. 5. Jakob.scholbach (talk) 16:48, 4 November 2008 (UTC)
I don't think that's a good resolution. That image has been there for a long time, and nobody challenged it until it got schedule to appear on the main page in a day or two. Why is that? Michael Hardy (talk) 16:54, 4 November 2008 (UTC)
- Probably because the person who challenged it didn't notice it until then? On enwiki, we would have assumed the image was fine because it was on commons. So it was unlikely to raise eyebrows during FA review. The issue is that someone opened a discussion on commons about the image, and so the image was removed here pending the outcome of that. — Carl (CBM · talk) 16:59, 4 November 2008 (UTC)
Unfortunately the vandals are winning, even if they fail to get the image deleted. They will probably prevent its schedule appearance at the top of the main page.
We need to find a good image quickly. The snowflake image is distinctly inferior, and I don't mean just as a work of visual art. It is inferior as a means of illustrating the mathematical idea that this is about. Michael Hardy (talk) 17:17, 4 November 2008 (UTC)
- Vandals? While those of us that have been around here for some time are familiar with your inimitable style, you should be aware there appear to be more impressionable onlookers that take such accusations to heart. --C S (talk) 17:50, 4 November 2008 (UTC)
OK, you don't like my style. But what about my actual point: We need to find a good image fast. Michael Hardy (talk) 18:15, 4 November 2008 (UTC)
- Hm, actually I wouldn't say I don't like it :-) Indeed, often I feel like expressing a similar sentiment. As for the image replacement, it's a shame but not a deal killer. Finding a better image is something that can be dealt with properly in time. As an idea, I suggest the 15 puzzle. It's a super old puzzle and should have no copyright issues. It's a nice layman example of group theory also. --C S (talk) 19:11, 4 November 2008 (UTC)
- Delay the appearance of the article on the front page if necessary until the discussion is over. Or alternatively since there are other people who independently made cubes, copyright is questionable especially if a generic drawing is used instead of a photograph. Delaszk (talk) 18:48, 4 November 2008 (UTC)
- I prefer the snowflake over the 15-puzzle, but I have to run now. Jakob.scholbach (talk) 19:16, 4 November 2008 (UTC)
- I don't see a rational argument that the cube is subject to US copyright. If the dispute is on commons, can't we pull it back to en.Wikipedia? — Arthur Rubin (talk) 19:23, 4 November 2008 (UTC)
- If someone has Rubik cube at home (unfortunately I don't have one where I'm now), you could take a picture and upload it to en.wiki. Chances are some self-appointed attorney for rubik.com will come here from commons, so a deletion discussion will likely start here as well. Based on their web site, rubik.com is an European company in an undisclosed EU country, so they'll have to do some footwork before they can send a DMCA copyright notice (update: maybe not). The whole affair is unclear because of the unclear status of Panoramafreiheit in the U.S. law. But on en.wiki fair-use can also be claimed, even though it cannot be claimed on commons. How do you explain what Rubik cube is without a picture? I think that fair use has a pretty strong case for a picture here. VG ☎ 19:32, 4 November 2008 (UTC)
- Note: I think it is crazy if this is not allowed. But, if it is deemed "non-free", then the front page won't accept a fair-use image. And it is unlikely that use in Group (mathematics) would be deemed non-replaceable. We therefore need more clarity on the legal position. Possibly the usage should be considered de minimis, since the cube is now such a well known quotidian object that it is unreasonable for Rubik's licensees to be considered to suffer any loss by its depiction. (cf "Not a significant taking", in U.K. law) Jheald (talk) 20:22, 4 November 2008 (UTC)
- OT remark: Is it really true that the law considers a photo of a three-dimensional toy a "derivative work"? "The law is a ass, a idiot." But then we already knew that. --Trovatore (talk) 19:57, 4 November 2008 (UTC)
- That's not OT. US law does not, in fact, consider the photo a derivative work. CRGreathouse (t | c) 20:13, 4 November 2008 (UTC)
- (ec) "Fair use" would only help on the article on the cube itself, not on this article. Perhaps the we could use Alexander's Star, or one of the other symmetry-based toys? — Arthur Rubin (talk) 20:17, 4 November 2008 (UTC)
- (to VG) Why do we need to take our own picture? Except for the recent change in the GFDL, couldn't we just use the present GFDL status on commons to copy it over, even if the uploader would be in a country where the copyright status is questionable? — Arthur Rubin (talk) 20:25, 4 November 2008 (UTC)
- That's not OT. US law does not, in fact, consider the photo a derivative work. CRGreathouse (t | c) 20:13, 4 November 2008 (UTC)
- If someone has Rubik cube at home (unfortunately I don't have one where I'm now), you could take a picture and upload it to en.wiki. Chances are some self-appointed attorney for rubik.com will come here from commons, so a deletion discussion will likely start here as well. Based on their web site, rubik.com is an European company in an undisclosed EU country, so they'll have to do some footwork before they can send a DMCA copyright notice (update: maybe not). The whole affair is unclear because of the unclear status of Panoramafreiheit in the U.S. law. But on en.wiki fair-use can also be claimed, even though it cannot be claimed on commons. How do you explain what Rubik cube is without a picture? I think that fair use has a pretty strong case for a picture here. VG ☎ 19:32, 4 November 2008 (UTC)
- I don't see a rational argument that the cube is subject to US copyright. If the dispute is on commons, can't we pull it back to en.Wikipedia? — Arthur Rubin (talk) 19:23, 4 November 2008 (UTC)
There's something to be said for Alexander's Star, but I think the Rubik's Cube picture much more clearly convey's the idea of transforming by turning one side, and that's what corresponds to the group's binary operation. Michael Hardy (talk) 21:42, 4 November 2008 (UTC)
Sometimes cowardly bullies win[edit]
Just wait until the preacher says "Speak now or forever hold your peace" to bring up something that could have been dealt with privately earlier, so you can make a public show of humiliating people to punish them for good work. That's what's happened here. This will be remembered for a long time. The story of this incident will be the whole content of the comprehensive biography of the persons responsible. A hundred years after the deaths of that person, or those persons (I don't really know who or how many), this is what they will be remembered for. This is all that they will be remembered for. Michael Hardy (talk) 01:11, 5 November 2008 (UTC)
- Would you please sign in on Commons:? It looks more like an anonymous rant, but, if I knew it was you.... — Arthur Rubin (talk) 03:01, 5 November 2008 (UTC)
Bigger cube?[edit]
I thought the article actually discussed the 3x3x3 cube's group. Since it doesn't, there are a number of images that are not of the 3x3x3 cube. It looks like the 4x4x4 cube is not produced by the same lame company [1], so I don't see an immediate problem, as there's no obvious copyright claim on the web to poke us with. BTW, a number of free screen savers use the 4x4x4 and 5x5x5 cube, but don't offer the 3x3x3 cube. I think I've figured out why :) VG ☎ 01:37, 5 November 2008 (UTC)
- I believe it would be okay. As far as I can find out the only protection they have for depictions of Rubik's cube is that it is a 3D trademark. They tried to assert copyright as an artistic design but I can only find a ruling in their favour for the design of the internal workings so they can't be shown. The trademark consists of a black 3x3x3 cube with stickers of the usual six colours on the sides. I don't believe the cube as shown could be confused with the trademark. Dmcq (talk) 01:57, 5 November 2008 (UTC)
- Nice solution, if it works! But would you mind toning down the glare from the flash a little bit? I don't know where my 4x4x4 cube got to so I can't take my own picture, but if you like I'll take a crack at yours in the GIMP late tonight West Coast time (probably too late to help, I guess). --Trovatore (talk) 02:03, 5 November 2008 (UTC)
- I didn't take this picture, found it on Rubik's_Revenge; I don't have a 4x4x4 cube. VG ☎ 02:06, 5 November 2008 (UTC)
- Nice solution, if it works! But would you mind toning down the glare from the flash a little bit? I don't know where my 4x4x4 cube got to so I can't take my own picture, but if you like I'll take a crack at yours in the GIMP late tonight West Coast time (probably too late to help, I guess). --Trovatore (talk) 02:03, 5 November 2008 (UTC)
Looks good. user:r.e.b.'s recently installed picture is better than the snowflake, but these Rubik-type things actually illustrate the motions. Can we get this installed fairly quickly? Michael Hardy (talk) 02:57, 5 November 2008 (UTC)
- Er no. If you go to the shop you'll find the 4 by 4, at the bottom they link to the same image rights. Erring on the side of caution it is mostlikely in break of IP. --Salix (talk): 07:34, 5 November 2008 (UTC)
- Hmmm. That's not the actual Rubik's Revenge site; of course the owner of the rights to Rubik's Cube is not going to go out of their way to remove legal notices which might still be correct. I don't think we have a problem without an explicit claim of copyright. As I noted earlier, there is no clear argument in favor of US copyright, even for images of the cube — but here we don't even have an explicit claim of copyright. — Arthur Rubin (talk) 15:24, 7 November 2008 (UTC)
Monty Hall problem[edit]
If anyone here has a moment or two, please comment on the Proposed Changes thread at talk:Monty Hall problem. -- Rick Block (talk) 03:48, 8 November 2008 (UTC)
Is there any point to this article or can it be deleted, redirected or merged? I'm not a maths person so I don't know. Cheers — Realist2 13:29, 7 November 2008 (UTC)
- The articles says the term applies to "external gears", so it should probably be merged into gear. It's just a dictionary definition at the moment, so certainly doesn't deserve its own article. --Tango (talk) 13:55, 7 November 2008 (UTC)
I've added some context and links to make the article more readily comprehensible. The user who created it also created a bunch of other severely stubby articles about gears with no initial context-setting. One of them read as follows (the whole article):
- Bottom land is the surface at the bottom of a tooth space adjoining the fillet
I'd have thought that was about dentistry rather than mechanical engineering (the article has improved since then). Michael Hardy (talk) 02:32, 9 November 2008 (UTC)
Linkable labels?[edit]
Is there a way to label an equation or something à la
- (1)
and have a label somewhere else ("equation (1)")? The link, much the same way as one has footnotes, should be such that if the reader clicks at the link, the equation or at least the label at the eqn. is highlighted in light blue. Jakob.scholbach (talk) 20:40, 7 November 2008 (UTC)
- How's this? Generalizing this is left as an exercise :-) Geometry guy 20:52, 7 November 2008 (UTC)
- Great. Thx Jakob.scholbach (talk) 21:21, 7 November 2008 (UTC)
- I've tweaked it a bit. The "float" CSS attribute was pretty much made for this. —Ilmari Karonen (talk) 12:06, 8 November 2008 (UTC)
- Great. Thx Jakob.scholbach (talk) 21:21, 7 November 2008 (UTC)
Exponentiation wars[edit]
Another contributor to the Exponentiation article wants to change it in a way I believe is very much against the ethos of an encyclopaedia. The latest discussion is at Talk:Exponentiation#exp(x). The other contributor Bo Jacoby (talk) is not about to go away soon, he has been trying to change various things in the article for the last three years. Is there a way of mediating or coaching so the exchange is a bit more fruitful, or do you judge that would be fruitless and the rumbling is at a low enough level that it can just go on for then next few years - or have you any other ideas for a more productive use of time? Dmcq (talk) 13:32, 8 November 2008 (UTC)
There is currently (or more rather a two years old) merge discussion on its talk page. Could an administrator please sort it out?
Topology Expert (talk) 08:40, 8 November 2008 (UTC)
Correction: The merge discussion is 11 months old (initiated by User:Arcfrk)
Topology Expert (talk) 08:42, 8 November 2008 (UTC)
- Merges can be done by anybody, simply copy the text over, merge it and make a redirect. Jakob.scholbach (talk) 12:36, 8 November 2008 (UTC)
The second of these three articles is mostly about comparametric plots. That part of it should get merged into comparametric equation. Michael Hardy (talk) 02:59, 9 November 2008 (UTC)
- The easiest thing to do is redirect parametric plot to parametric equation, which I've now done. --Salix (talk): 01:36, 10 November 2008 (UTC)
Regiomontanus' angle maximization problem[edit]
I have created the article titled Regiomontanus' angle maximization problem. Probably it could profit from other points of view. Everybody's seen this problem in a calculus course, but I think it is far less well known that there's a simple solution via elementary geometry. In addition to those two, I've included a solution by simple algebra. Michael Hardy (talk) 03:02, 9 November 2008 (UTC)
- The article looks great. There is lots of detail but perhaps a reference of at least one calculus book could be given (to justify that this is a common problem in calculus textbooks; funnily enough, I have never heard of this problem!). Also, maybe some more linking can be done but I think that the article is very good as it is.
Topology Expert (talk) 11:31, 9 November 2008 (UTC)
Thank you. I'll cite at least one textbook. Michael Hardy (talk) 02:27, 10 November 2008 (UTC)
Skolem's paradox[edit]
A new editor, user:Xzungg, is repeatedly making some POV edits to Skolem's paradox. I have integrated the positive parts of his edits into the article already, and commented on the talk page. I could use the assistance of a couple other editors to help determine a consensus about the article content. — Carl (CBM · talk) 14:20, 9 November 2008 (UTC)
- We have the article Wikipedia:What Wikipedia is not but (as far as I know) we do not have the article What mathematics is not. Dear experts in mathematical logics, would you please create it? It could help... I mean, math is not The Ultimate Consistent Complete Theory Of Absolute Objective Truth; etc.
- More specifically: a universal computer allows for creation of virtual computers inside; and similarly, a mathematical universe (be it Platonistic, or just a model of axioms) contains "virtual math universes". A program running on a virtual computer cannot check whether it is real or virtual (assuming no bugs in virtualization); similarly, mathematics cannot check whether its universe is "real", not "virtual". Thus, the goals most important for philosophers are mostly not reached by mathematics. This is OK with us. If someone assumes they are reached, and then gets a contradiction, it is his contradiction, not ours. Boris Tsirelson (talk) 11:11, 10 November 2008 (UTC)
- I'm dizzy.... Ryan Reich (talk) 15:30, 10 November 2008 (UTC)
- You ask, what's that all about. Well, it is about the Skolem paradox, and the standard comment to it, that the notion of a countable set is not absolute. I want to say that the latter could be explained to a wider audience in less technical way, maybe, using a metaphor of virtual computer (or something like that). By the way, I am now typing this on a virtual computer. From the outside it appears to be a file rather than a computer. Likewise, an uncountable set within a model of the set theory may be countable if you look from the outside. Boris Tsirelson (talk) 16:44, 10 November 2008 (UTC)
- This thread is an example of the non-absoluteness of topicality, for sure. Ryan Reich (talk) 16:54, 10 November 2008 (UTC)
- Sorry, if so. However, did you look at the discussion of Skolem paradox? There, user:Xzungg insists that the paradox refutes (in some sense) the set theory, thus, the mathematics. I want to say that it refutes rather some exaggerated philosophical demands to mathematics. Boris Tsirelson (talk) 17:01, 10 November 2008 (UTC)
- Oh, I see. This might help more in the talk page discussion, though. Ryan Reich (talk) 18:04, 10 November 2008 (UTC)
Kevin Houston[edit]
I have nominated the biography Kevin Houston for deletion at Wikipedia:Articles for deletion/Kevin Houston. Please feel free to comment there, but please use tact, since the discussion is public and there's a decent chance Houston may read it someday. — Carl (CBM · talk) 14:29, 10 November 2008 (UTC)
The Core Contest[edit]
Hi,
This is Bill Wedemeyer, a biochemistry professor at Michigan State University. I apologize that this message is not directly related to mathematics, but please bear with me for a moment. I've come to ask for your help, especially the help of my fellow professors.
I recently became aware of The Core Contest, which was run last year for a few weeks (Nov 25 – Dec 9). Briefly, it was an article improvement drive focusing on basic articles that belong in the "core" of an encyclopedia, with awards of $100 promised for the five most improved articles. For example, one of the articles was Hypatia of Alexandria, which belongs to this WikiProject.
My impressions are that (1) the contest was remarkably successful in improving articles and (2) many younger students threw themslves into it, body and soul, partly for the fun of it but also in the hopes of winning the prizes. Unfortunately, circumstances seem to have conspired to prevent those prizes from being awarded.
I'd like to amend this and reward the prizes, as they were promised. I'm willing to sponsor the awards myself, but I hope you agree that it'd be more fun and more wiki-spirited if we all joined in. I'm especially interested in recruiting professors, who I think will want to be kindly to poor but hardworking students, especially in this season of many holidays. We probably all remember what it was like to be a poor student.
I've contacted Prof. Martin Walker (one of the judges of the contest) about the matter, and he's very supportive. Please contact me by e-mail if you're interested in donating to the cause. We would plan on announcing the winners in two weeks, on November 25th, the anniversary of the contest.
Thank you, Proteins (talk) 18:31, 10 November 2008 (UTC)
- An interesting initiative. I have sent an email to B.W. Boris Tsirelson (talk) 19:04, 10 November 2008 (UTC)
- That sounds like an excellent idea. I am a student myself, so won't get involved (I didn't take part in the contest, though), but I fully support it. Are you planning on restricting it just to students or everyone that entered? I don't know who proportion of entrants were students, but I doubt all were. --Tango (talk) 19:10, 10 November 2008 (UTC)
- In principle I also think it's a good idea. I have my doubts, though, whether a student (I'm a student myself) will be able to write a GA/FA article on articles like Algebra or Calculus. These topics are just huge in scope. A goal that is more achievable, IMO (and what I'm currently trying to do), is to bring "basic" top priority articles that are usually at least partly taught in undergrad to better shape. There is still lots of things to say, but the topics are somehow more bounded. Jakob.scholbach (talk) 19:23, 10 November 2008 (UTC)
- That sounds like an excellent idea. I am a student myself, so won't get involved (I didn't take part in the contest, though), but I fully support it. Are you planning on restricting it just to students or everyone that entered? I don't know who proportion of entrants were students, but I doubt all were. --Tango (talk) 19:10, 10 November 2008 (UTC)
I'm glad that the first responses are so positive, and that people aren't mad at me for posting something off-topic. It's true that writing good articles about topics so vast in scope is hard, although it's also true that many might benefit from such articles. I don't mean to say that these articles are more important, or more crucial to the success of Wikipedia than, say, group (mathematics). As a professor, I think my own articles would have to be specialized, too; by report, professors' knowledge has increased and their scope narrowed so much that they know practically everything about practically nothing. ;) My interest in the Core Contest is purely personal. It pains me to see students working hard and then disappointed, and I suspect that others will want to join me in setting things right. Proteins (talk) 19:43, 10 November 2008 (UTC)
PS. My special thanks go out to Prof. Tsirelson, the first person to write me and volunteer his help!
The Irrational Number Generator for deletion[edit]
Proposed, anyway. It's not categorized yet, but would be somewhere in Mathematics. — Arthur Rubin (talk) 15:16, 7 November 2008 (UTC)
- Delete. Pointless, non-notable, unreferenced. Algebraist 15:44, 7 November 2008 (UTC)
- You can use the template {{prod2}} on the article, if you want whoever closes the prod to know your opinion.
- A tangential point: when you say "unreferenced", I think you mean "not published anywhere because it's not very interesting". But "unreferenced" literally means "no references are provided", and there are lots of articles in that state which certainly should not be deleted (Hilbert–Smith conjecture?). New editors sometimes read comments like this and get the impression that it's the lack of sources, rather than the lack of interest, that's the problem. So I think it's important for us to use very clear statements in deletion debates. In this case, the issue with this article is that the result discussed is, at best, an exercise in a textbook, and not interesting enough to warrant an article. — Carl (CBM · talk) 16:20, 7 November 2008 (UTC)
- It could be mentioned in Fermat's Last Theorem as a mildly interesting corollary (some kind of source to suggest notability would be required, though), that's about it. --Tango (talk) 18:58, 7 November 2008 (UTC)
- When I said unreferenced, I didn't mean that this was a sufficient reason for deletion. I meant that the only thing that could save a pointless result from deletion (i.e. being widely mentioned in the literature despite being pointless) is not the case. Anyway, the prod has been disputed for some reason so it's at AfD. Algebraist 19:48, 7 November 2008 (UTC)
- But it's not a corollary of FLT; this follows immediately from the Fundamental Theorem of Arithmetic. Septentrionalis PMAnderson 20:11, 7 November 2008 (UTC)
- A tangential point: when you say "unreferenced", I think you mean "not published anywhere because it's not very interesting". But "unreferenced" literally means "no references are provided", and there are lots of articles in that state which certainly should not be deleted (Hilbert–Smith conjecture?). New editors sometimes read comments like this and get the impression that it's the lack of sources, rather than the lack of interest, that's the problem. So I think it's important for us to use very clear statements in deletion debates. In this case, the issue with this article is that the result discussed is, at best, an exercise in a textbook, and not interesting enough to warrant an article. — Carl (CBM · talk) 16:20, 7 November 2008 (UTC)
- No need for a resurrection drive here. Other than Fermat's Last, this really isn't necessary. AGK 19:27, 7 November 2008 (UTC)
As for this article, sure, let's delete that. However, to take us slightly off topic, let me point out that the theorem that the kth-root of a natural number n that is not a kth-power is irrational is of significance historically. For example, Theodorus claimed to have proven the square root of n (except 4, 9, and 16) up to 17 is irrational, and explanations of how he could have done this form a non-negligible body of scholarship. Part of the speculation rests on the assumption that he did not know the fundamental theorem of arithmetic. Indeed, as pointed out in Hardy and Wright's text on number theory, the fundamental theorem of arithmetic is not required for the proof that kth-root of a natural number n that is not a kth-power is irrational. Elementary methods analogous to that of proving square root of two is irrational can be used. --C S (talk) 21:06, 7 November 2008 (UTC)
- I have my copy of Hardy and Wright (fifth edition) at hand. I think you are referring to Section 4.5. They do not say that it is possible to prove Theorem 44 (the irrationality of kth roots of non kth powers) without FTA. Rather, they give a discussion of how to prove specific cases of the irrationality of square root of N.
- I have given some thought to this, and I do not see how it is possible to prove Theorem 44 in general without using Euclid's Lemma, which in turn is equivalent to FTA. Note that Euclid's Lemma itself can be verified in any specific case with only a finite amount of computation: for intsance, if 3 | ab, then multiplying out (3k+1)*(3l+1), (3k+1)*(3l+2), (3k+2)*(3l+2) and seeing that none of them are divisible by 3 proves the result. Plclark (talk) 04:05, 9 November 2008 (UTC)
- Well, in order for the equation () not to have a solution outside Z, it is sufficient that that the domalin Z is integrally closed; while the FTA notes that Z is a unique factorisation domain. Being a UFD is strictly stronger than being an integrally closed domain; c.f. e.g. . Thus, at least for some domains, there are "easier" proofs than by means of first proving that they are UFD's (since the latter is false and thus hopefully:-) unprovable). However, I do not know whether there is a known easier proof for Z. JoergenB (talk) 16:28, 12 November 2008 (UTC)
Buried deep within Wikipedia...[edit]
...are things that sit there for LONG periods of time with no attention from anybody. For SEVERAL YEARS now, this has sat in the article titled Gottfried Leibniz:
- Leibniz is credited, along with Isaac Newton, with the discovery of infinitesimal calculus. According to Leibniz's notebooks, a critical breakthrough occurred on 11 November 1675, when he employed integral calculus for the first time to find the area under a function y = x.
y = x. That's what it said. The graph of that equation is a straight line; the area under it is the area of a triangle. Obviously Leibniz was not the first to find the area of a triangle; obviously you don't need integral calculus to do that. I've changed it to read as follows:
- Leibniz is credited, along with Isaac Newton, with the discovery of infinitesimal calculus. According to Leibniz's notebooks, a critical breakthrough occurred on 11 November 1675, when he employed integral calculus for the first time to find the area under a function y = ƒ(x).
Note that I changed "the" to "a". Several years ago, this got quoted on the main page and consequently ridiculed here on this page, and then it got fixed on the main page. But not in the Leibniz article. People may argue about whether Archimedes' various quadratures that anticipate Leibniz's work but did not use the fundamental theorem of calculus mean that the words "for the first time" are right. But the part where it says y = x is so idiotic that one should wonder: is there some way of making the process of bringing Wikipedia's content before the eyes of knowledgeable people can be made systematic enough that glaring things like this will be seen? Michael Hardy (talk) 22:40, 11 November 2008 (UTC)
- It would be interesting to know what exactly he wrote in his 1675 notebook. Did he use the notation f(x)? What kinds of things could he integrate or differentiate? Was it sums of powers of x or something like that? When did he differentiate f(x)g(x) or f(g(x))? Dmcq (talk) 00:41, 12 November 2008 (UTC)
- I teach Calc 1 and my first two examples in integral calculus is to calculate the area underneath a constant function (area of rectangle), and y=x (area of the triangle). It is not a question whether the examples are trivial it is whether the method is. So it is possible that Leibniz's first applications of his new method were the rectangle and triangle as well. (Igny (talk) 01:18, 12 November 2008 (UTC))
- I am far from an expert on the history of calculus, but I believe the article was correct. Leibniz was a smart guy, so of course he tested his new method on a question he already knew the answer to. --Tango (talk) 01:41, 12 November 2008 (UTC)
If the article was correct, it really needs to get phrased differently from the way it was. Michael Hardy (talk) 04:36, 12 November 2008 (UTC)
I understand what you mean. It is sometimes frustrating to have an article where absolutely no-one bothers to read or add to the discussion page. If I post a comment one day, I probably won't get a reply for at least a year. But I have to deal with it. That is why most of the time I follow the following:
a) If it is a 'popular' article to edit, I comment at the discussion page and someone will probably see my comment within a week and respond.
b) If it is unlikely that someone will ever respond to my comment (if I make one), I will probably just make the edit I want to anyway (saves a lot of time and trouble).
Maybe there should be some sort of way of monitoring a page (other that watching) that involves a group of editors who discuss changes to the page in question quite often. On each page we could have a list, and editors could add themselves to that list provided that they monitor that page frequently (at least once per month). If many editors participate in this 'project', they could be evenly distributed over most of the math articles. I don't know whether this is a good idea but I think it is at least a slight improvement compared to the features we have now.
Topology Expert (talk) 13:55, 12 November 2008 (UTC)
Occurrence-in-subtuple problem[edit]
Occurrence-in-subtuple problem has been "prod"ed. Does anyone know anything about this? Michael Hardy (talk) 13:51, 15 November 2008 (UTC)
- I've removed the "prod" tag and done some editing. It is probably less obvious than it was that the person who wrote this is not a native speaker of English (e.g. I changed "what is regulated of it" to "what is regulated by it", and I made a number of analogous changes). But I'm wondering if this article has a counterpart in some other language and should be linked to it? The article still suffers from some deficiencies in the first author's understanding of how to write Wikipedia articles, and of how best to explain mathematics problems. Michael Hardy (talk) 14:08, 15 November 2008 (UTC)
Ultrafilter lemma vs. cardinality of bases[edit]
The vector space article currently says: "The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a given vector space have the same "size", i.e. cardinality.[citation needed]" Can somebody provide a reference for this, please? I didn't find one. Thanks, Jakob.scholbach (talk) 14:25, 15 November 2008 (UTC)
- "Bases in Vector Spaces and the Axiom of Choice", James D. Halpern, Proceedings of the American Mathematical Society, Vol. 17, No. 3 (Jun., 1966), pp. 670-673. JStor. — Carl (CBM · talk) 14:54, 15 November 2008 (UTC)
- The relevant passage in the article now reads:
- Every vector space has a basis. This fact relies on Zorn’s Lemma, an equivalent formulation of the axiom of choice.[17] The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a given vector space have the same "size", i.e. cardinality.[18] It is called the dimension of the vector space, denoted dim V. Given the other axioms of Zermelo-Fraenkel set theory, the latter statement is equivalent to the axiom of choice.[19]
- Yes, thanks for pointing it out, it was indeed a mis-restructuring of mine. It's fixed now. Jakob.scholbach (talk) 21:13, 15 November 2008 (UTC)
Show/hide button not working[edit]
In the "solution by algebra" section in Regiomontanus' angle maximization problem, I've put in a show/hide button that's not working. Can anyone figure out why? Michael Hardy (talk) 20:16, 10 November 2008 (UTC)
- I'm not sure why you want to use {{show}} in article space, but the problem seems to be equals signs being interpreted as template parameters. Geometry guy 20:37, 10 November 2008 (UTC)
Why I want to do it would be clear from what I wrote there, I would think. I know others have done this in various other math articles. Has this problem occurred elsewhere? Michael Hardy (talk) 22:06, 10 November 2008 (UTC)
- I appreciate your thanks for the fix. The articles linking to {{show}} are here. The obvious mathematical one is Mathematical induction, where the idea was introduced here. Do others think that this practice is a good idea? We show/hide navigation templates, comments, discussions, debates. Should we be doing this with content? Geometry guy 23:29, 10 November 2008 (UTC)
- Personally I do not support the use of hidden content within articles. When the issue is that certain boring derivations take up too much space, the solution is usually to remove the derivations. Unless there is some encyclopedic interest in a proof or derivation, it should be omitted. But if there is encyclopedic interest, then the derivation shouldn't be hidden from sight by default. — Carl (CBM · talk) 00:12, 11 November 2008 (UTC)
- Sometimes clicking on a link takes you to another place on the same page. The major thing I'd have against it is that some people switch off javascript and currently it looks like the default is that such people have the text hidden and can't show it. I'm sure they could fix it somehow so the default would be that if one has no javascript the text is shown. So basically my only objection is people haven't done it, rather they put the text into a section further down like an appendix or to another article and link to that. I think I could grow to like it if it was introduced as a general idea. Dmcq (talk) 02:24, 11 November 2008 (UTC)
It's not about hiding "boring derivations"; it's about hiding things that interrupt the main line of argument that is the point of the section or paragraph or passage, but that might nonetheless be of encyclopedic interest.
Also we have a policy requiring articles to be accessible to a broad audience. This furthers that policy. Michael Hardy (talk) 03:36, 11 November 2008 (UTC)
- I agree with Carl and others above. Jakob.scholbach (talk) 10:00, 11 November 2008 (UTC)
- A suggestion - a simpler derivation is
- - which is simply an application of completing the square - and then note that as x is always positive, the first term takes a minimum value of 0 when . Then the whole section in question can be omitted. Gandalf61 (talk) 10:50, 11 November 2008 (UTC)
- How is that simpler? It's the same thing except that you're working only with the numerator, and it's LONGER than why I wrote in the article (as long as you don't expand the hidden content). Michael Hardy (talk) 17:17, 11 November 2008 (UTC)
- I don't see how it replaces the hidden section. It's clear how you go from right to left in the equality
- but many people will still wonder how you go from left to right. And that's what the hidden section explains. Michael Hardy (talk) 18:05, 16 November 2008 (UTC)
- I don't see how it replaces the hidden section. It's clear how you go from right to left in the equality
- Re M. Hardy: in many cases, we can "write around" the derivations, as would be done in regular published mathematics, so that readers who want to skip the derivations can just skip to the next paragraph.
- When I was talking about "boring derivations" I was referring to the reader's view; I should have found a better way to say it. Both examples I have seen of the use of hidden content involved relatively basic algebraic manipulations, rather than deep content. So I'm not convinced that they need to be in the article, even for accessibility (this is the ancient textbook/encyclopedia controversy). But if they do warrant inclusion, I think they should just be included, even if it requires some work to write compelling prose around them.
- Another option for including parenthetical comments is to put them in footnotes. Then they are not in the middle of the section, but also are not "hidden". — Carl (CBM · talk) 14:24, 11 November 2008 (UTC)
- Putting the derivations in a special footnote section at the bottom of the page is a good idea. You might consider using the "group=" property of the ref and references tags to handle derivations independently of the normal inline citations and footnotes. For example, you could write < ref group="derivation" > I've added an example to this sandbox.
- Here's another compromise that you all might consider. A little context first: at the Accessibility project, we've been discussing how to make math-mode text accessible to visually-impaired users, who rely on screen readers such as JAWS to hear Wikipedia articles. The simplest two solutions seem to be (1) don't use the math tag (rather draconian), or (2) add ALT text in the math-mode material as in the formula
- A third approach with potential is to introduce internal structure to math formulas so that scripts could act on them, to produce accessible ALT text automatically and, more ambitiously, to carry out various symbolic math calculations. This third approach can work for showing derivations as well. To illustrate this approach, I've written a prototype script User:Proteins/showmathderivations.js that you can import into your monobook.js page, which you can test out on this sandbox. It produces a tab labeled "d" at the top of the page, next to the "watch" tab. When clicked, the script displays the derivation in a popup window. The derivation itself is encoded in the page; in the sandbox, it's done explicitly, but I'm sure that you all see that it could be done very easily with templates. This gives students and other interested people the chance to see the derivation, whereas uninterested people need not even notice its existence. Nor would the derivation take up room in a Notes section. Proteins (talk) 15:50, 11 November 2008 (UTC)
I actually like the idea of the show/hide button. It is something an online encyclopedia can do but which a paper one cannot do, so it should be exploited! There are many cases when a casual reader would not want all the details of a proof/derivation, but someone really trying to understand the topic would want to read. MSGJ 17:45, 11 November 2008 (UTC)
- An online encyclopedia can also cause the text to blink, which cannot be done in print. — Carl (CBM · talk) 22:05, 11 November 2008 (UTC)
- Well that feature should definitely be implemented. Especially on all the "boring derivations" ;) MSGJ 14:18, 12 November 2008 (UTC)
- ...and also there are times when a reader adept in algebra (or whatever) would rather skip such routine steps, whereas to another reader they would not be routine. Michael Hardy (talk) 22:42, 11 November 2008 (UTC)
- I'll have a go at seeing if there isn't a way of ensuring the hidden text is shown if the user has disabled javascript. That's my chief objection to it currently. Probably is possible with a noscript tag surrounding some css but I won't have time today to check it. Lots of people disable javascript if at all possible as it cuts down a vector for viruses - and you know to what length some people interested in maths will follow logic. Dmcq (talk) 08:53, 13 November 2008 (UTC)
- I googled with 'noscript javascript css hide' and it came up with quite few instances of people dealing with this problem. It seems to rouse quite a bit of interest and people mention the accessibility problem if it isn't done. It looks like it would be worthwhile dealing with generally, and dealing with it isn't too difficult though requiring a little thought to avoid a problems. The main problem seems to be to that the obvious method of having the text visible and the javascript hiding it causes the page to flicker nastily whilst it is being rendered, it's better to use javascript in the head which links in a bit of css which hides the text. I haven't the foggiest how such a problem is fixed in wikipedia. Dmcq (talk) 21:53, 16 November 2008 (UTC)
Number theory stub template[edit]
I also changed this template to the one User:Ben Tillman put instead of the previous algebra stub template. Again this is more representative of number theory (and that is why I changed it (I don't really think having the numbers 0,1 and 2 is useful although 1 and 0 may have some (slight) significance)). Hopefully there are no objections but if you have any, please post them and I can discuss.
Topology Expert (talk) 05:56, 16 November 2008 (UTC)
- The wording and formatting of stub templates is quite standardized; I don't think there's any reason to add a note "this template is not part of the article". If that note is needed because the image used might be misleading, then another image should be found. — Carl (CBM · talk) 11:42, 16 November 2008 (UTC)
\emptyset versus \varnothing[edit]
Does anyone else have an opinion on this?
The former, using \emptyset, looks like something that shows up because you're using an old-fashioned typewriter with a correspondingly limited character set, so you type the digit 0 and then backspace and type a slash over it. So I prefer the latter, using \varnothing. Michael Hardy (talk) 19:17, 16 November 2008 (UTC)
- I didn't even know \varnothing existed, but I like it better. Nice catch. Ryan Reich (talk) 19:26, 16 November 2008 (UTC)
- Same with me. Jakob.scholbach (talk) 19:49, 16 November 2008 (UTC)
- For the sake of semantics, I would say we should use \emptyset when talking about the empty set (it makes it easier for people reading the code, if nothing else). It should be possible to change the font so that it looks better, though, since \varnothing is certainly better. I don't know enough about LaTeX to know how one would do that (it will certainly require a request to the sysadmins, though). --Tango (talk) 19:52, 16 November 2008 (UTC)
- The fonts are what they are; mediawiki essentially just uses a vanilla LaTeX installation to compile the images. Knuth designed the emptyset symbol intentionally, which is why varnothing has the "var" prefix. — Carl (CBM · talk) 19:57, 16 November 2008 (UTC)
- I actually write , rather than , even in handwriting, and I always thought that was general practice. I am a model theorist, so pretty close to set theory, and in the rare instances when I see in print I always feel that that's an excentric choice.
- Just so that Michael Hardy's justification of his aesthetical decision doesn't remain unanswered, in my opinion is much worse because it tends to jump out of the text. For me it's analogous to printing every zero in bold. --Hans Adler (talk) 21:09, 16 November 2008 (UTC)
- Somehow I'm failing to see it jump out of the text any more than any other character either in mathematical notation or in plain-text sentences. Michael Hardy (talk) 22:57, 16 November 2008 (UTC)
- I was talking about printed articles or books. The symbols tends to be about two to three times as wide as what I consider the normal one, and is often not from the same font as many other mathematical symbols. --Hans Adler (talk) 23:38, 16 November 2008 (UTC)
- Somehow I'm failing to see it jump out of the text any more than any other character either in mathematical notation or in plain-text sentences. Michael Hardy (talk) 22:57, 16 November 2008 (UTC)
- I don't really like either of them that much, but between the two I prefer . To me looks like a 1950s-cartoon version of the planet Saturn. Or maybe just a generic planet. Which of course is a planet contained in all dense open sets of planets. --Trovatore (talk) 21:43, 16 November 2008 (UTC)
- Like Michael, Ryan, and Jakob, I prefer \varnothing too. But so what? Is it important? We generally follow the stylistic choices of the earliest principal editor. Geometry guy 21:56, 16 November 2008 (UTC)
- Heh. Let me demonstrate my ignorance, once again. I always assumed that \emptyset on TeX was some sort of font design mistake that was never fixed. Never occurred to me that someone might actually use that symbol in real life. linas (talk) 04:27, 17 November 2008 (UTC)
- That's how it's always seemed to me too. Michael Hardy (talk) 05:06, 18 November 2008 (UTC)
- Heh. Let me demonstrate my ignorance, once again. I always assumed that \emptyset on TeX was some sort of font design mistake that was never fixed. Never occurred to me that someone might actually use that symbol in real life. linas (talk) 04:27, 17 November 2008 (UTC)
- Like Michael, Ryan, and Jakob, I prefer \varnothing too. But so what? Is it important? We generally follow the stylistic choices of the earliest principal editor. Geometry guy 21:56, 16 November 2008 (UTC)
- The fonts are what they are; mediawiki essentially just uses a vanilla LaTeX installation to compile the images. Knuth designed the emptyset symbol intentionally, which is why varnothing has the "var" prefix. — Carl (CBM · talk) 19:57, 16 November 2008 (UTC)
Is there really no choice of font? When I make an \emptyset in pdflatex, on my own LaTeX installation, it comes out nicer than the one here. See this screenshot: ![]() . Aspect ratio seems to be about 3:2 (not counting the slash) whereas the WP one is more like 2:1, which seems too much. --Trovatore (talk) 07:01, 17 November 2008 (UTC)
. Aspect ratio seems to be about 3:2 (not counting the slash) whereas the WP one is more like 2:1, which seems too much. --Trovatore (talk) 07:01, 17 November 2008 (UTC)
- Hmm, OK, the difference isn't that extreme. I fiddled around a little, blowing up the images in Eye of Gnome and measuring them with KRuler and (while it's a bit subjective deciding where the "edge" is) it looks like the aspect ratio for the WP \emptyset is around 1.94 : 1, whereas the one that shows up on my LaTeX is about 1.83 : 1. Not a huge difference, but enough that the WP one does come out a bit scrawny, whereas I think the one that my setup gives is perfectly fine.
- Still, I like even the scrawny WP \emptyset better than \varnothing. --Trovatore (talk) 07:41, 17 November 2008 (UTC)
- Personally, I prefer JRSpriggs (talk) 16:57, 17 November 2008 (UTC)
- Seriously, or are you joking? That notation works alright stand-alone (though even there the fact that it's two glyphs instead of one is problematic), but as soon as you include it inside another set notated with curly braces, it gets confusing very quickly. --Trovatore (talk) 21:30, 17 November 2008 (UTC)
- Personally, I prefer JRSpriggs (talk) 16:57, 17 November 2008 (UTC)
\large character in math formatting[edit]
Is there a way of forcing a character to be bigger or smaller in tex on WP? I tried out \large and some options in \mbox but it complains about anything I do. I notice for \varnothing people were getting screen images to make it larger so I guess it's not possible, but my reading of tex says I should be able to do something like \mbox{\large 0} but I can't get anything along those lines to work. Dmcq (talk) 15:26, 17 November 2008 (UTC)
- There is some limited control of sizing possible by using \displaystyle, \textstyle, \scriptstyle, and \scriptscriptstyle. —David Eppstein (talk) 17:51, 17 November 2008 (UTC)
"Occurrence-in-subtuple problem" on AfD[edit]
Occurrence-in-subtuple problem, an article about a combinatorial problem said to have applications in genetics, has been nominated for deletion. It is obvious that the reason for some of the imperfections in writing is that it was written by someone who is not a native speaker of English. That of course is a reason to clean it up, not to delete it. The substantial objection seems to be an allegation of original research, concerning which I have no settled opinion. Michael Hardy (talk) 05:11, 18 November 2008 (UTC)
Hilbert's thirteenth problem[edit]
Can someone provide precise statements of the theorems of Kolmogorov and Arnold that are mentioned in a hand-waving way in Hilbert's thirteenth problem? Some sources on the web speak of "superposition", which I usually think of as meaning addition, but some other speak of "composition", which I usually think of as something quite different from addition. The Wikipedia article ought to give a precise statement of the problem if possible. Michael Hardy (talk) 06:11, 18 November 2008 (UTC)
Algebra stub template[edit]
I have seen the template:
(removed now that discussion is over becase otherwise this page would be classified as an 'algebra stub' once archived)
on several pages and I was wondering whether this template could be changed (this maybe a bit difficult and I don't know the rules so I am assuming that this can be done). The reason being is that it does not really reflect what 'algebra (modern)' is; rather it reflects high school algebra. Maybe in a way it reflects field theory (in a vague way!) but it does not reflect group theory very well. I think that there could be a more 'representive' symbol. Any opinions?
Topology Expert (talk) 11:20, 9 November 2008 (UTC)
- Yes, we can change the image if desired. One advantage of the square root symbol, even if it's not great, is that it's instantly recognizable by a fifth-grader. I don't know how you would make an image of similar size to represent more advanced concepts from modern algebra. And I'm afraid that if we had a picture that was supposed to represent something advanced, few people would be able to even tall what the picture meant. — Carl (CBM · talk) 12:56, 9 November 2008 (UTC)
But I am not sure that fifth-graders are supposed to understand this. Moreover, a fifth grader would probably interpret the symbol as 'high-school algebra' (which is rather reasonable for someone who has never heard of the subject). Perhaps we could still make it 'easy to understand' and 'representative of modern algebra'?
I agree with what User:Delaszk said because the most appropriate symbol would probably be one that reflects the fundamental idea behind group theory (and that is of course the binary operation). Could we implement this or do we need more people to agree?
Topology Expert (talk) 00:50, 10 November 2008 (UTC)
- Go ahead and implement it. If someone doesn't like it, they can always revert and we can discuss it further. --Tango (talk) 01:00, 10 November 2008 (UTC)
- I am not exactly sure how to implement it... I know that the page is [2] but I am not sure where I can find an image like a*b=c.
Topology Expert (talk) 07:57, 10 November 2008 (UTC)
Could someone please tell me how (and I could do it)?
Topology Expert (talk) 07:39, 15 November 2008 (UTC)
- How about that? It's the simplest equation I could find on commons Ben (talk) 09:22, 15 November 2008 (UTC)
- I think that image would be better for number theory (after all Fermat's last theorem is the most famous theorem of number theory). So I changed it. Topology Expert (talk) 05:43, 16 November 2008 (UTC)
- I think I prefer the old one actually. MSGJ 09:36, 15 November 2008 (UTC)
- I think that image would be better for number theory (after all Fermat's last theorem is the most famous theorem of number theory). So I changed it. Topology Expert (talk) 05:43, 16 November 2008 (UTC)
- The problem with a lot of "images" nowadays is that they aren't proper images. They use transparent colors or background colors, which means if your browser is set up to be be white text on black background then all these "images" disappear, including the main wikipedia logo. Delaszk (talk) 10:33, 15 November 2008 (UTC)
- I have finally changed the image to a more 'representative' one. Since modern algebra is based on the binary operation (just as topology is based on a topology), this certainly represents modern algebra and its 'close relative' (I think category theory first developed from a group theoretical model so this is what I mean by 'close relative') category theory.
- The previous image a^n + b^n = c^n was alright but it still did not represent modern algebra (more like Fermat's last theorem which I would classify as number theory). This looks much better and gives a better impression of mathematics(don't you hate it when people think that mathematics is about 'summing numbers up'?). Topology Expert (talk) 05:37, 16 November 2008 (UTC)
- By the way, I removed the template at the beginning of this discussion for otherwise this page would be classified as an 'algebra stub' once archived. Topology Expert (talk) 05:40, 16 November 2008 (UTC)
- The number theory one looks fine on this PC, but the algebra one is huge. See Affine Grassmannian for example, where the stub template is almost as big as the rest of the article. It may be just this computer, but it would be good if others could check this out please. Ben (talk) 06:15, 16 November 2008 (UTC)
- Thanks for the feedback. On my PC, it does not look as large. I will play around with the template a little to make it visible as well as small but anyhow this template is the 'best representative' of modern algebra (by the way, the previous (sqrt(x)) template was almost as big as this one). Topology Expert (talk) 06:22, 16 November 2008 (UTC)
- How about now (It think 200px is the minimum size possible without making it invisible to the naked eye)? Topology Expert (talk) 06:25, 16 November 2008 (UTC)
- Thanks for the feedback. On my PC, it does not look as large. I will play around with the template a little to make it visible as well as small but anyhow this template is the 'best representative' of modern algebra (by the way, the previous (sqrt(x)) template was almost as big as this one). Topology Expert (talk) 06:22, 16 November 2008 (UTC)
- The number theory one looks fine on this PC, but the algebra one is huge. See Affine Grassmannian for example, where the stub template is almost as big as the rest of the article. It may be just this computer, but it would be good if others could check this out please. Ben (talk) 06:15, 16 November 2008 (UTC)
- By the way, I removed the template at the beginning of this discussion for otherwise this page would be classified as an 'algebra stub' once archived. Topology Expert (talk) 05:40, 16 November 2008 (UTC)
I'm just wondering why these stub templates need images at all. Would not
- This algebra-related article is a stub. You can help Wikipedia by expanding it.
suffice. What encyclopedic purpose does the image really serve, they just take up screen space and distract the eye.--Salix (talk): 08:22, 16 November 2008 (UTC)
- TopExp, I understand the reasons you have for changing this image, but I think this one is too complicated and will distract people from the content of the article. It's too big, and as you say it can't be reduced without making the symbols unreadable. All we want is a simple image. MSGJ 08:46, 16 November 2008 (UTC)
- Thankyou for your opinions. I would not say that this template is too big (maybe a bit larger than the previous sqrt (x) template) and furthermore it gives a (fairly simple) representation of the binary operation using a commutative diagram. I can't see anything complicated about this image either (if someone understands what a commutative diagram is then he/she would probably understand the mathematics behind the template). Could we please just keep the image? I have even added that the image is not part of the article so there is no confusion and I don't think that it will distract people from the content of a particular article. See locally finite group for an example. In this article, the template fits in nicely.
- TopExp, I understand the reasons you have for changing this image, but I think this one is too complicated and will distract people from the content of the article. It's too big, and as you say it can't be reduced without making the symbols unreadable. All we want is a simple image. MSGJ 08:46, 16 November 2008 (UTC)
As I have mentioned already, a simple image such as sqrt(x) or a^n + b^n = c^n is representing the wrong field of maths (one representing arithmetic and the other is representing number theory). I can get a different image and try it out, perhaps, if other people also disagree entirely with this image. But I think (and I hope others do to) that we need a proper image and all the previous ones were not at all satisfactory.
Topology Expert (talk) 09:55, 16 November 2008 (UTC)
Take the current {{Cattheory-stub}} template which is basically (not mathematically) the same as this one.
Topology Expert (talk) 09:58, 16 November 2008 (UTC)
What about this one:
that illustrates the compatibility of two different structures on a field (that make it into a bialgebra). If not this one, I would say that the following image could also work (quite a simple commutative diagram that illustrates the associativity of monoids (assoicativity is something that a fourth grader could understand)):
Any opinions?
Topology Expert (talk) 10:42, 16 November 2008 (UTC)
- Now that I'm home and I've looked at this on my own computer, I am leaning towards not supporting this change. Even though the image is smaller than it was earlier, it's still much bigger than it should be. It seems to me these templates are designed to entice readers/editors to add to the article and help humans/bots to categorise them. Are there any other uses? If not, then I don't see that an image is going to make that much of a difference. An image may add a bit of life to otherwise bare articles, or they may help humans quickly refine a categorisation (maths stub -> algebra stub with a quick glance at a familiar image), but a massive commutative diagram isn't any better then a discrete square root symbol in these cases. I'm also worried about the notice, inside the template, telling people that the template isn't part of the article. Are most readers going to know what a template is? I've been here for three years and I'd still ask myself what this commutative diagram is doing here before realising it's part of the template. I think it's best to keep things simple here - a square symbol might not be the best representative for algebra, but surely it's good enough? Ben (talk) 10:47, 16 November 2008 (UTC)
- What about
- Jakob.scholbach (talk) 11:03, 16 November 2008 (UTC)
- That looks brilliant, but I thought there was some issues with that image? Or have they been resolved? Ben (talk) 11:08, 16 November 2008 (UTC)
- Well, if you look here, I think consensus is leaning towards keeping the image. I personally also think that the deletion discussion is pretty much nonsense. Jakob.scholbach (talk) 11:16, 16 November 2008 (UTC)
- That looks brilliant, but I thought there was some issues with that image? Or have they been resolved? Ben (talk) 11:08, 16 November 2008 (UTC)
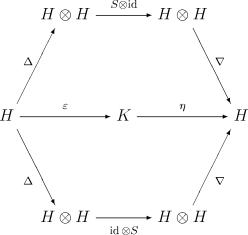
Unfortunately, no one seems to understand my point. My point is that we want something that represents modern algebra. Not some junk like a square root symbol that makes an ordinary person believe that mathematics goes as far as a square root (and believe me, there are people who think this). Furthermore, this is not the sole purpose of the image. We also want the image to represent a fundamental idea behind group theory. I do like the image given by Jakob.scholbach, but a cube does not represent the fundamental idea behind group theory. A concept such as the binary operation or a commutative diagram that illustrates the compatibility of two different structures on a field would really represent this field of mathematics better (the binary operation would be the best). If you want something easier to understand (now lets face it, there are mathematicians who don't know much group theory (or category theory)), then choose something like this:
This commutative diagram represents the associativity of the binary operation in a monoid (which would be understood by any real mathematician). We definitely can't (and don't want to) aim for an average (non-mathematician) to understand the image; we want the image to be understood by someone who has had some decent formal training in mathematics (or who is learning group theory). And anyone who knows what a function is would probably understand a (simple rectangular) commutative diagram.
So if you don't like the current image, the one I just suggested may be better. Any opinions? If there is still disagreement, I can try for another image but I would like to have the opinions of several mathematicians.
Topology Expert (talk) 12:21, 16 November 2008 (UTC)
- I think I understand what you are after. I do think the Rubik's cube represents quite well what a group, and a fortiori a binary operation, is. For practical matters
- seems to me hardly useful, since one cannot decipher what it is about. Moreover, when I see a commutative diagram, I don't think of algebra first, more of category theory. Possibly one has to find some sort of compromise between easiness in grasping the image's content and conveying enough of the idea one has in mind. This can be very challenging (compare it to a three(!)-word explanation of a topic). Jakob.scholbach (talk) 12:30, 16 November 2008 (UTC)
Thanks for the opinion. What I don't understand is why we can't make the image 100px which is not too large and is still (reasonably) visible to the naked eye:
Why wouldn't this work?
With regards to algebra and category theory, I am quite confident when I say that category theory was invented based on algebra and then expanded to other fields of mathematics. For instance, 'isomorphism' is common to both fields and I can list quite a few others which are active terms in algebra as well as in category theory. If you analyse the commutative diagram carefully, it basically illustrates (the fact) that in a monoid, the binary operation is associative.
Topology Expert (talk) 12:57, 16 November 2008 (UTC)
As I mentioned earlier, one cannot decipher what the current category theory stub template is about either ({{Cattheory-stub}}) but that has been there for a long time. At least 100px is visible and not too large. Why in Wikipedia, does everything have to follow strict rules?
Topology Expert (talk) 12:59, 16 November 2008 (UTC)
- Well, I mean we can make it a little bit bigger, too. Nobody, however will "analyse the diagram carefully", people just glance at such things. Also, I think an undergrad guy or a physicist, say, will probably in general not know commutative diagrams at all. But as somebody said above, it is not terribly important what image we choose. The more important thing is to get the templates removed by writing sufficient articles. Jakob.scholbach (talk) 14:44, 16 November 2008 (UTC)
I agree with what you say about the importance of the image. But at least this image is better than sqrt(x) and I bet that someone who knows calculus could easily learn what a commutative diagram is. Furthermore, we don't expect everyone to understand it; as long as an algebraist can understand it, its fine. The image should just be a representation of the field and not part of an article, so people are not expected to understand the image.
Topology Expert (talk) 03:45, 17 November 2008 (UTC)
- To me the new image conveys the message that algebra = category theory. Is that accurate or desirable? —David Eppstein (talk) 04:05, 17 November 2008 (UTC)
- I guess you (as well as other mathematicians) see it that way but I don't. My initial purpose was to have an image like a*b = c but that does not really make much sense as it is. Instead I thought something more 'representative' such as assoiciativity of monoids which are fundamental in algebra (and other fields) would be appropriate. Mathematically, the current commutative diagram is equivalent to: Let (M,*) be a monoid and let a, b and c belong to M. Then, (a*b)*c = a*(b*c). This also works in semigroups but most people would probably interpret M as a monoid. So if you look at it that way, the image does not convey that algebra = category theory, but rather it represents a fundamental axiom in algebra (the other image regarding the compatibility of two different structures over a field that make it into a bialgebra could have worked but was more specialized and was probably a bit advanced for the general reader).
Topology Expert (talk) 06:05, 17 November 2008 (UTC)
I can't believe there's serious debate over whether abstract algebra should be represented by a 75px image of a commutative diagram, no matter how algebraic the fact it encodes. The idea, in addition to being absurd from a visual design perspective, borders on the snobbish: why does the stub template have to represent some fact of "real" math, one phrased in a language that, admittedly, is not understood or appreciated by most students and a good number of practitioners? Anyone who sees this stub, however amateur at algebra, should understand that it's talking about something they might know; ask yourselves if, as undergraduates, you would have had that reaction to the associativity square. I think this point is amply supported by Topology Expert's own words: if a calculus student could "easily learn", or someone familiar with functions could "probably understand" a commutative diagram, then it is too complicated; we should not be arguing over whether the picture is potentially comprehensible, but whether it is thematically suitable. We may not care whether non-mathematicians get it, but we had better not be so elite as to dismiss college students (or, God forbid, analysts :) ).
Furthermore, category theory is totally unnecessary for understanding what algebra is about, and writing associativity as a commutative diagram is obfuscatory unless there's a more general game afoot. Granted, saying "algebra is square roots" is rather a dumbification, but not every level of abstraction below the One True Abstraction gives a misleading picture of the subject. Algebra, in itself, is a subject concerned with sets, elements, and operations, not objects and arrows (however much about the former they reflect), and understanding it at just that level is enough to, say, get you a Fields Medal, if you do it right. Ozob's suggestion is an excellent one: it expresses a fact basically characteristic of algebra (if you see a binary operation, and it's associative, then you are in the midst of defining an algebraic structure) in a concise way that, if you learned any algebra at all, you learned this first. Ryan Reich (talk) 01:23, 18 November 2008 (UTC)
- I'm on board with not doing the arrow-chasing, but I like the Rubik version better. More eye-catchy. Plus non-associative algebra is still algebra. --Trovatore (talk) 01:26, 18 November 2008 (UTC)
- I have to go but just one point: Most college students would know what a commutative diagram is; won't they? Also, objects and arrows are involved in every maths (most basic notation: f: X -> Y).
Topology Expert (talk) 04:05, 18 November 2008 (UTC)
- I suspect it's not even true that most college mathematics majors would know what a commutative diagram is. But as for "most college students": certainly not. —David Eppstein (talk) 04:13, 18 November 2008 (UTC)
- Everyone in this discussion appears to know what a commutative diagram is. Furthermore, some editors here are probably students (my assumption). I am not saying that someone has to know category theory (or even what it is) to be a mathematician but the image I have given is mathematically equivalent to the one given by User:Ozob.
Also, category theory is the centre of mathematics and every single branch of mathematics has objects and arrows anyhow.
Non-associative algebra may still be algebra but you will have to agree that associativity (except for closure of course) is the most fundamental axiom in algebra.
Topology Expert (talk) 04:38, 18 November 2008 (UTC)
- Lots of people in this discussion are grad students or worse, and no one here is one of those storied casual editors who drives by a stub and throws in his two cents, at whom one assumes the template (and all its connotations) are aimed. That's the group you want some instant recognition from. Even among mathematicians, the assertion that there are always objects and arrows is probably going to raise some eyebrows; I mean, by that standard you can express Riemannian geometry as and other silliness. What you are arguing is the philosophical complement of what you started out denouncing: first the tag was oversimplified to the point of being misleadingly trivial; you now explicitly advocate it being overgeneralized to the point of being obscuringly deep.
- Now, my life situation being what it is I can't but agree that category theory is the bomb, but I don't think that point can be argued in an icon attached to a cleanup tag, and believe me when I say that most people, even mathematically-inclined people, would not understand it in the spirit you intend it. Ryan Reich (talk) 05:39, 18 November 2008 (UTC)
- Point: I don't say mathematics is about objects and arrows; I say that objects and arrows are there everywhere in mathematics. Topology Expert (talk) 06:26, 18 November 2008 (UTC)
- I have learnt one thing from this overwhelmingly long discussion: In Wikipedia, there is too much talk and too little action. Why waste time creating talk pages and discussing when by the time the discussion is over, people forget what they wanted to do initially (or what they were discussing about)? In my opinion, this discussion was a waste of time (for everyone). If people really hate the commutative diagram, I can let them have their way. But I have been in this discussion too long to give up.
Take this massive comutative diagram for instance:
How else would you describe what a Hopf algebra is (unless you want to tediously find a series of equations that are equivalent to this commutative diagram)? Commutative diagrams are a easy (and natural) way of storing information and are everywhere in advanced mathematics. I am probably telling you what you already know, but my point is that you shouldn't be afraid to include a commutative diagram in a supposedly 'lower level' mathematics like algebra. Furthermore, I can also bet you that everyone who knows algebra well, will also know what a commutative diagram is. Isn't that what we want?
Topology Expert (talk) 06:44, 18 November 2008 (UTC)
- Nobody is arguing (here) that category theory is somehow a waste of time. But that's beside the point. We have a separate stub sorting category for category theoretic stubs. Shouldn't we be aiming for something that would set algebra apart a little more from that? And besides, the diagrams fit very badly into the small size. I like the a(bc)=(ab)c idea expressed earlier, or even the Rubik's cube one, much better. —David Eppstein (talk) 06:49, 18 November 2008 (UTC)
- Some of you are contradicting yourselves. First, you say that you don't want a commutative diagram because it is distracting and eye-catchy; now you are saying that you want something eye-catchy like a Rubik's cube. I don't mean to attack but I vote for at least as User:Ozob mentioned if not a commutative diagram. Associativity is fundamental and a Rubik's cube is rubbish (we are dealing with all forms of algebra; not just finite group theory).
Topology Expert (talk) 02:00, 19 November 2008 (UTC)
- Well, it's not like everyone who doesn't like the diagram idea has to agree on exactly why. But as far as I'm concerned, the problem with the diagram isn't that it draws too much attention to itself. It's that it draws attention to itself in a bad way — the likely reader reaction is "what the heck is that smudge?". Whereas the cube is instantly recognizable and visually attractive.
- As for "associativity being fundamental" to algebra, so you don't accept the octonions as an algebraic structure? --Trovatore (talk) 02:10, 19 November 2008 (UTC)
- Just to take the tangential mathematics off the table: octonions: algebraic, yes; fundamental, maybe not; associative, definitely not, but the absence being notable makes it just as important as a negative property. A lot of the exotic algebraic structures (e.g. Moufang loops) are premised on some compensation for nonassociativity. Ryan Reich (talk) 03:01, 19 November 2008 (UTC)
- Well, that's a little convoluted as a reason to include the associative law on a stub involving the octonions. But that isn't my real objection; it's just a response to TE. My real objection is that it's boring and formalistic-looking. (Unfortuately for {{mathlogic-stub}} I wasn't able to think of anything that wasn't boring and formalistic-looking; for algebra we have a good candidate and should use it.) --Trovatore (talk) 03:08, 19 November 2008 (UTC)
- Maths is not suppose to look fancy. Keeping things like a Rubik's cube gives the wrong impression about mathematics (people may think that the Rubik's cube is the highest level math there is). As for associativity, I never said that all algebraic strucutures are associative; most algebraic structures are and that is exactly why associativity is fundamental. Are you saying that it is not?
(By the way, associativity is to groups as Hausdorff is to topological spaces. Many mathematicians don't care about non-Hausdorff spaces but that does not mean that Hausdorff spaces are unimportant).
Topology Expert (talk) 03:28, 19 November 2008 (UTC)
Why would you think that is boring? When I first learnt about these infinite cardinalities, I was fascinated (and excited to prove by myself that ).
Topology Expert (talk) 03:35, 19 November 2008 (UTC)
- I certainly didn't say (the object) is boring! It's the symbol for it that's not terribly inspiring. Still, it does have some visual interest, with the Hebrew calligraphy — the associative-law thing doesn't even have that. --Trovatore (talk) 05:07, 19 November 2008 (UTC)
- Sorry about the misinterpretation. I think that after maybe 50 years, about every mathematician will read Wikipedia (even sooner perhaps). Algebra, as you will probably agree, is the most widely known (as in well-understood) mathematical subject (apart from calculus) by mathematicians. By putting this tag (commutative diagram) we are encouraging mathematicians (and college students) to find out what it is about and this will certainly make category theory more widely known. Isn't this what we want? The bonus is that it still has a lot to do with algebra.
Topology Expert (talk) 05:15, 19 November 2008 (UTC)
Great! I just thought of something much better (represents algebra well, very easy to understand, and also quite important)! What about an exact sequence? We could choose a simple sequence consisting only of three objects. For instance:
Practically everyone knows that represents the integers and practically everyone has a vague idea as to what the arrows are (a function). This would be more exciting as an image, more concise, and much better than a dinosaur commutative diagram. Any opinions on whether or not this would be preferable to a commutative diagram?
Topology Expert (talk) 05:28, 19 November 2008 (UTC)
- It's probably a bit better than the commutative diagram, if only because it's easier to read (the aspect ratio is a bit wide, though). But it's not as good as the Rubik's cube. No purely symbolic token is going to be. --Trovatore (talk) 05:33, 19 November 2008 (UTC)
- I suppose it is not as good as the cube because the cube is colourful. If you notice, every stub template in mathematics is a symbolic token (except for the geometry stub template). Why not follow this convention?
As I mentioned, we want to expand people's knowledge (one purpose of Wikipedia) and this stub template is excellent for this (allows people to learn about the mathematical subject of category theory).
Topology Expert (talk) 05:46, 19 November 2008 (UTC)
Well, if I were feeling cynical, I could point out that most of the students in a course I'm teaching never heard of Euclid until I mentioned his name (I don't know how you can do that and be a high-school graduate) and they certainly don't know what the blackboard bold letter Z represents. And guess what they "know" that the arrows mean? Here's an example:
That what "almost everybody knows" the arrows mean. Michael Hardy (talk) 05:54, 19 November 2008 (UTC)
There are two things that I have learnt in the past 10 days:
a) Wikipedia can be a big waste of time sometimes (good fun though)
b) The world is a lot dumber than I thought
(you must really get sick of teaching your students; I don't know how you do it)
Topology Expert (talk) 06:31, 19 November 2008 (UTC)
The Rubik's cube has the following flaws:
1. It is too colourful and gives the wrong impression of mathematics (people may think that to solve a Rubik's cube, you need to be good at maths and if you can solve it, you must be the best mathematician around (believe me, people think this already; we don't want to give them encouragement)).
2 (more importantly). It only represents finite group theory and does not have a wide scope. One user mentioned that the commutative diagram only represents associative algebra; at least it represents a wider scope of algebra compared to the Rubik's cube.
Any arguments against my points? (some support would be much appreciated)
Topology Expert (talk) 08:06, 19 November 2008 (UTC)
Because of the apparent stupidity of the outside world, I want to make a point that this template should only be aimed at real mathematicians (any mathematician knows what an exact sequence is (or at least what an arrow means (or Z (hopefully)))).
Topology Expert (talk) 08:11, 19 November 2008 (UTC)
- No, it shouldn't only be aimed at real mathematicians. It should be aimed at anyone who can expand the algebra stub. Knowing what a commutative diagram, exact sequence or arrow represents are not prerequisites to this. Honestly, people aren't going to take anything away from the image, instead they will take away something from the text "This is an algebra stub ...". We shouldn't be worried about the image representing all of algebra any more than an author worries about an image on the cover of their book representing all of its contents. It's just for show, so a simple representative should be fine. Ben (talk) 09:57, 19 November 2008 (UTC)
- Just answer this to yourself: don't you want people to understand what mathematicians do? Aren't you sick and tired of non-mathematicians confidently saying that mathematics is only about numbers and arithmetic? Well I am. All I want to do with this is:
a) Give an image which people (who don't know maths) are clueless about so they stop talking nonsense
b) Give an image which is really important in the intersection of mathematics with algebra
Commutative diagrams are wonderful for both purposes. As I mentioned, the image that User:Ozob suggested is mathematically equivalent to the commutative diagram and furthermore, gives more meaning to mathematics.
You are probably sick and tired of me arguing so I won't argue for so long. I just wanted to emphasise that:
a) The Rubik's cube is unsatisfactory (in my opinion) for the reasons I have already mentioned
b) User:Ozob's image is mathematically equivalent to mine
(You probably don't want me arguing any longer and as you said, it doesn't matter what image we choose; the words are more important. Since no one (except for me) is going to analyse the image, we might as well keep the commutative diagram unless of course it discourages people from expanding a stub (which is unlikely)).
I just wanted to make one quick (and very important point); algebra is a subject which almost any mathematician (and student) knows at least a little bit about. Therefore (with the number of algebraists around), any algebra stubs must contain really deep concepts within the field (because very few people would have known enough to expand it and hence it is a stub). So really, anyone who can expand an algebra stub, will probably know algebra well and hence what a commutative diagram is. The more simpler concepts can be edited by college students because they won't be stubs (generally between stub and good article mostly).
Topology Expert (talk) 12:45, 19 November 2008 (UTC)
Also (to Brwian), category theory is very important in mathematics (see category theory and perhaps homological algebra for an example). Topology Expert (talk) 12:54, 19 November 2008 (UTC)
- Homological algebra ? Well of course homological algebra! That goes without saying. But apart from homological algebra, what has category theory ever done for us ? Brwian (talk) 13:46, 19 November 2008 (UTC)
- Don't you want people to understand what mathematicians do? Aren't you sick and tired of non-mathematicians confidently saying that mathematics is only about numbers and arithmetic?
- I don't really worry about what they think, but regardless of what I worry about, I do think the mathematics pages here (as opposed to a small image attached to a minor template sitting at the bottom of a select few pages) are more than enough to convince them otherwise. Now, I'm not quite sure I follow your argument. You list 'ignorance of mathematics' as a motivating factor for this image change, but earlier you said these stub templates should be designed for real mathematicians. Now you're arguing that only advanced topics are stubs, but a quick scan of the algebra stubs shows plenty of 'basic' to undergraduate topics, Trinomial for instance. I don't think there is any good reason to think your proposal will change a single persons mind, but if any user points to one of the stub tag images and proclaims "See, mathematics is just numbers, arithmetic and Rubik's cubes!!", I'll gladly eat my words :) Ben (talk) 13:33, 19 November 2008 (UTC)
To Brwian: what about sheaf theory?
Topology Expert (talk) 02:54, 20 November 2008 (UTC)
OK, so there are a few basic concepts which are stubs. If I make them 'unstubs' now, we can accept the commutative diagram? I will start with trinomial.
Topology Expert (talk) 02:58, 20 November 2008 (UTC)
- You keep missing the point. The diagram doesn't look good. It's not a sensible idea to try to use the image in a stub template to stimulate interest in a subject; that's beyond its scope. The point of the image is to distinguish the various stub types with an appealing, and at least somehow relevant, icon. You're trying to read (or write) way too much into it. --Trovatore (talk) 03:42, 20 November 2008 (UTC)
(edit conflict) Most of the users have bailed this discussion so I think the vote is pretty much, 'who cares', although some users still strongly hate the commutative diagram. My point is that the commutative diagram encourages editors to learn about category theory. Have a look at this and you will find that the template is more descriptive and people will not think that it is a smudge anymore. Furthermore, the new description encourages readers to learn about category theory: a bonus because anyone who knows calculus (well, unlike Michael Hardy's students) will be able to learn the basics of category theory.
Topology Expert (talk) 03:50, 20 November 2008 (UTC)
- Please understand that I understand your comments. However, this diagram still represents algebra and anyway, all mathematics is based on category theory. So why not keep an image like that? Besides, the icon is still relevant.
Topology Expert (talk) 04:06, 20 November 2008 (UTC)
- I'm sorry, but that picture just says "category theory" to me. And no, I do not agree that algebra (as a whole) and category theory (as a whole) are in any way fundamental parts of each other. Why the intense insistence on using the template for advocacy? The stub template is not even really a part of the encyclopedia; people are not expected to learn anything from it, but simply be alerted that the article could be expanded. Putting in a lofty emblem says to the less fluent, "We really meant that someone smarter should improve this article", and to the more fluent, "There really isn't any point improving this article unless you can put in some commutative diagrams". Simply, the notions of category theory are not common indicators for algebra, so they will be received as requesting similarly uncommon response. As they sometimes say it, this kind of picture is POV (and this discussion proves it).
- As you can see, not everyone has "bailed", and from what I read in the more recent responses, the vote (which it is presumptuous for you to summarily dismiss in your favor) is unanimously (minus one) "No, don't use the diagram. It's ugly, confusing, philosophically overburdened, and wrongheaded." It may have been said politely in various roundabout ways, but there it is. Ryan Reich (talk) 04:13, 20 November 2008 (UTC)
- Update: I have put the associativity equation into {{algebra-stub}}. Maybe it's not ideal, but you are the only one who thinks it is less ideal than your commutative diagram, which it replaces. Ryan Reich (talk) 04:18, 20 November 2008 (UTC)
- I find your response quite rude. My intentions were good and I seem to have wasted my time trying to find a good image for nothing (I even tried to reason with something apart from the commutative diagram). Obviously, none of what I have done is appreciated.
Topology Expert (talk) 04:49, 20 November 2008 (UTC)
- I have responded on your talk page, since this is now a private matter. Ryan Reich (talk) 05:35, 20 November 2008 (UTC)
I have a better idea. There was no agreement over which image to use (some people liked the rubik's cube, some preferred the associative rule, some people don't give a monkeys). However there does seem to be consensus that the image is not very important - it's the text that is important. So I have removed the image and just left the text. I agree this discussion has gone on far too long. TE it is understood that your intentions are entirely good; however you should have realised earlier that your opinions were not gaining support. MSGJ 09:53, 20 November 2008 (UTC)
- Well I realized after I had argued for one page (ask yourself what you would have done in the same situation if you had argued for that long and, more importantly, strongly believed that the image was appropriate).
- However, I prefer User:Ozob's image and so does User:Ryan Reich. If you strongly don't want that image, hold a vote but I think for know I will keep the image Ryan chose. Hopefully, in the future when more mathematicians participate, I will get more support and then I may change the image. But I will leave it for now.
Topology Expert (talk) 11:17, 20 November 2008 (UTC)
- I've changed the equation from a statement into a question since there are plenty of interesting nonassociative algebras. In particular I've just come across gyrovector spaces, a brilliant way of looking at hyperbolic geometry and special relativity. P.S. I studied maths, but none of the courses were on category theory. As an aside, it does seem interesting that Galois theory can be generalized into a purely category theoretic setting, not that I understand any of it. ("Galois Theories", Francis Borceux, George Janelidze, Cambridge University Press, 2001) Delaszk (talk) 18:54, 20 November 2008 (UTC)
- In my opinion that equation is just too big and distracts. Perhaps we could make a decision on this and close this ridiculous thread? MSGJ 19:10, 20 November 2008 (UTC)
So in TE's style, please type below: (No reasons/discussion required, thanks.)
- 0, for no image at all
- 1, for the Rubik's cube
- 2, for the associativity equation (with or without the question mark)
- 3, for other (but unless the others can agree it's not going to win)
Votes will be counted tomorrow. MSGJ 19:12, 20 November 2008 (UTC)
- I vote 3 for . This includes both associative and nonassociative operations. Delaszk (talk) 20:11, 20 November 2008 (UTC)
- I vote for 1, the Rubik's cube. Eye-catching, instantly recognizable, and vaguely on-topic is better in this very restricted context than mathematical accuracy. But my second choice would be for 2, the associativity equation. —David Eppstein (talk) 21:51, 20 November 2008 (UTC)
- I say the Rubik's cube. It's a waste of oxygen to argue about the deeper meanings of template images; the important criteria are distinctiveness and aesthetic appeal. Of course it should also have something to do with the topic, but as long as there's a connection, we don't have to argue about the details of the connection. --Trovatore (talk) 21:58, 20 November 2008 (UTC)
- 2, associativity, no question mark. We just ended one debate about using a mathematical in-joke and now another is proposed? And Rubik's cube is too distinctive for my taste. Ryan Reich (talk) 23:26, 20 November 2008 (UTC)
- 1. The associtivity equation(s) might be better from a mathematical point of view, but it's too big and distracting to be placed on pages will little content. The cube is recongnisable even when it's tiny. Ben (talk) 23:31, 20 November 2008 (UTC)
- Anyone of them (I don't really care which one is chosen now. If it really matters, we can review the image after 6 months or so (when there are more voters)). But I just wanted to make a note about 'associative' and 'non-associative' algebra; earlier, the image was sqrt (x). Did that represent modern algebra at all? Take the Rubik's cube. Does that represent anything apart from group theory (or even finite group theory)?
Topology Expert (talk) 23:53, 20 November 2008 (UTC)
I know that I am alergic to stub templates but how about this one:
Since most people here want a 'geometric' image of group theory, this one is perfect. It is also quite clear and reperesents the circle as a group (in fact a Lie group; the circle is one of the most common, simple examples of these).
What Delaszk said explains something: algebra has a lot to do with category theory (and as I mentioned, category theory originated from algebra (hence the term 'isomorphism')). Maybe one day, category theory will be a huge part of algebra (galois theory, in my opinion, is a mix of category theory and algebra!).
Topology Expert (talk) 01:14, 21 November 2008 (UTC)
How does this look?. I suggest looking at:
before judging (every college student who does algebra will know that the circle is a group with multiplication).
Topology Expert (talk) 02:36, 21 November 2008 (UTC)
Huh? On Locally finite group and Affine Grassmannian, the associativity equation appears but on Trinomial, no image appears! There must be an error because of so frequent changes (or maybe it just comes up like that on my computer).
Topology Expert (talk) 02:41, 21 November 2008 (UTC)
Current good article nominations[edit]
I have nominated the vector space article for WP:Good article nomination#Mathematics. I'd be thankful if people around could have a look, particularly those knowledgeable in analysis. Jakob.scholbach (talk) 09:28, 18 November 2008 (UTC)
P.S. There are two other current nominations (nominated by other editors), Mayer-Vietoris sequence and Robert Hues. I'd like to encourage people to review articles. It's fun, usually pretty interesting and helps the author of the article a lot. Thanks, Jakob.scholbach (talk) 09:36, 18 November 2008 (UTC)
- I just spotted something wrong in "Banach spaces" section of "Vector space" (see the discussion page). Boris Tsirelson (talk) 07:53, 19 November 2008 (UTC)
- Can't it be a featured article (haven't read it yet but I will do so now)?
Topology Expert (talk) 07:54, 19 November 2008 (UTC)
- Well -- "can't" is a bit the wrong question ;). It needs somebody to work on it further, push it through the pretty tedious FAC and so on. I haven't decided yet whether I'm up to it. The question is a little bit: an additional (estimated) 5% of article quality needs an additional 50% of work. Spending this time on other articles that are not yet so well-developed may be more fruitful. One thing I can recommend to everybody, though: take a maths-rating category, and take the top-priority class articles in there. Pick one article and move it (by editing it appropriately) two steps up, e.g. from Start to B+ etc. I'm focussing on algebra-top-priority at the moment. Jakob.scholbach (talk) 19:48, 19 November 2008 (UTC)
Strange software bug?[edit]
First:
- \frac{z}{e^z-1}=\sum_{n=0}^\infty \frac{B_n}{n!} z^n
Second:
- \frac{z}{e^z-1}=\sum_{n=0}^\infty \frac{B_n}{n!} {z^n}
First, within "math" tags:
Second, within "math" tags:
At radius of convergence, this first form was failing to get rendered. Why? Michael Hardy (talk) 23:30, 18 November 2008 (UTC)
- No-one's sure why, AFAIK. For some reason, the server generates a corrupt image for the first code, and this image has to be manually deleted by someone with server access to allow the server to generate a non-broken image. Because the second code is different, the server doesn't use the (broken) cached image but generates a new one instead. Algebraist 23:38, 18 November 2008 (UTC)
The problem seems to have been fixed. I edited the article and it looks good now. Michael Hardy (talk) 18:14, 19 November 2008 (UTC)
DYK participation[edit]
DYK has started keeping track of which article have received the most page views while being featured on the Main Page. See Wikipedia:DYKBEST. DYK would like to make its section of the Main Page more effective. We are in need of Wikipedians who can review the raw Wikipedia:DYKBEST data and come up with factors that make it more likely that an article will receive page views. If interested, please feel free to review the data and edit Wikipedia:DYKBEST#Features_of_an_effective_DYK_hook. Thanks. -- Suntag ☼ 08:22, 20 November 2008 (UTC)
Geometry stub template[edit]
Don't fear the heading; wait till the end of my message. A non-mathematician keeps reverting my changes to this but I found a perfect image. To make this discussion short, have a look at this. Then type either 1 (for agree with my image) or 0 (if you disagree). No explanations required. If my image is not favourable (after 5-7 people vote), I will immediately revert my inclusion of that image. Please decide on the basis of the image rather than the previous discussion and also note that my image represents the connected sum (differential geometry). Anyone can understand that the image illustrates two objects being glued together and furthermore, this is more representative than a dodecahedron.
Topology Expert (talk) 11:49, 20 November 2008 (UTC)
If necessary, the image size can be increased by a few pixels and this should make it more clearer.
Topology Expert (talk) 11:51, 20 November 2008 (UTC)
- Oh dear TE. Comments like:
- Do you know any mathematics? .. you would not understand the difference between the two images in question. [3]
- aren't going to win you any arguments. Wikipedia isn't mathematicians vs. the world. It's a community project that anyone is allowed to join and make contributions to. Various policies should, and do, dictate what stays, goes and changes, not a persons qualifications. Can I recommend you leave the stub templates alone for a while? Ben (talk) 12:18, 20 November 2008 (UTC)
- 0, sorry. MSGJ 12:12, 20 November 2008 (UTC)
- 0, too Jakob.scholbach (talk) 12:16, 20 November 2008 (UTC)
- 0. Ben (talk) 12:18, 20 November 2008 (UTC)
- 0 (note also that connected sum is a topological notion more than a geometrical one.) (TimothyRias (talk) 12:39, 20 November 2008 (UTC))
- 0. The idea of the image is invisible without a microscope. Michael Hardy (talk) 14:21, 20 November 2008 (UTC)
Ok (you don't have to say sorry by the way). First of all, I had a dispute with User:Moondyne regarding something else and he threatened to block me. Next, he started tracing my edits and reverting them (these edits were mathematics-based). I didn't mean to be rude, but I am trying to expand Wikipedia. If users threaten to block me, be rude (User:Moondyne), don't agree with me (I think users are against me now but I can't do anything about it) and undo my edits, then it seems that it would be best if I retire. And I know that no one really would care if I retired (I have better things to do anyhow (as everyone here does)). I also don't see why User:Ben Tillman had to bring something irrelevant into this discussion.
I have to keep my promise, but the image I put up is representative of geometry (differential geometry in fact and also has very important applications in fibre bundle theory), small and clear, easy to understand, and probably the same as the previous image except for the fact that they represent different topics. What is the problem (you don't have to answer this and if no-one does I might as well revert my inclusion of that image)?
Topology Expert (talk) 12:48, 20 November 2008 (UTC)
By the way, there was an edit conflict and I just wanted to note that the connected sum belongs to differential geometry.
Topology Expert (talk) 12:48, 20 November 2008 (UTC)
- The connected sum image is invisible. You need a microscope to see it. I clicked on the image in the template and saw the larger picture and only then could I tell what it was. Michael Hardy (talk) 14:19, 20 November 2008 (UTC)
Please note also that many of the articles in {{geometry-stub}} are about things Euclid would recognize as geometry, which may be very different from the things a modern mathematics department's hiring committee would recognize as geometry. —David Eppstein (talk) 15:32, 20 November 2008 (UTC)
- This discussion fits in with the one about the difference between priority and importance in the article ratings. A nice picture of a dodecahedron like there was before probably would have greater priority. Dmcq (talk) 15:43, 20 November 2008 (UTC)
You may as well revert then. I thought it was quite visible but that's my opinion. Anyway, Euclid was 2000 years ago, as far as I know no-one works in Euclidean geometry any longer.
But now that I look at it, maybe I will vote 0 as well.
Topology Expert (talk) 23:44, 20 November 2008 (UTC)
- While we're holding votes, here's another: is Topology Expert a troll or just an insufferable snob? WP:AGF would argue for the latter, I suppose, but it seems shocking to me that I would have to defend Euclidean geometry as a subject of interest here, or for that matter as a subject of research, despite its unpopularity among more-serious-than-thou mathematicians. —David Eppstein (talk) 01:10, 21 November 2008 (UTC)
- Because a plurality of my edits have been in the area of general topology, I have had many interactions with Topo over a long period of time. First, I firmly believe that he is not a troll: he means well, and most of the time he is civil, listens to others, and is amenable to reason. I also think insufferable snob misses the mark. Do remember that anyone can represent themselves any way they choose on Wikipedia. If your username is David Eppstein, it's pretty easy to confirm that there is an eminent computer scientist / mathematician named David Eppstein, and anyone who watches the contributions of User:David Eppstein can decide whether or not they think the two David Eppstein's are one and the same. (I certainly do.) Similarly, if you search on mathscinet you will find that there is a (younger) mathematician P.L. Clark, and then you can make up your own mind whether User:Plclark is that mathematician. But calling yourself "TopologyExpert" does not make it so, no more than having an expert mathematician userbox does: if you look on the list of wikipedians who self-identify in this way, you will find that there is very little overlap with the known professional mathematicians who are regularly involved with Wikiproject Mathematics. (One such self-identified expert mathematician is thirteen years old.) Let me just say that I think it is unwarranted to assume that Topo has done published/publishable research in topology and/or that he has a PhD in mathematics. To be clear, he doesn't need to have either of these qualifications to contribute to the mathematics articles on wikipedia. I just want you to realize that your appraisal that you are defending -- or even need to defend -- more venerable fields of mathematics against some mathematical elitist may not be accurate. Plclark (talk) 09:41, 21 November 2008 (UTC)
- I agree. From the gaps of knowledge that this "expert topologist" has exhibited in the past (I can look up the details if necessary) it is clear that they are at most a first-year student. --Hans Adler (talk) 10:09, 21 November 2008 (UTC)
- Please no WP:OUTING. If I was a 13 year old and said nothing about it that would be my business. Lets just look at the content of the contributions. Dmcq (talk) 11:17, 21 November 2008 (UTC)
- Obviously the problem is not being a 13 year old, but behaving like one. I am not following this user around, so I can't make a general statement. But at least some of their contributions have been problematic. We are used to somewhat clueless contributions coming from laypeople; but when they come from someone who seems to claim the authority of an expert, they become much harder to deal with. Especially for those of us who are still not sure they are not dealing with a colleague. (Btw, WP:OUTING doesn't apply here, although I admit that other, related, policies arguably do.) --Hans Adler (talk) 11:59, 21 November 2008 (UTC)
- Because a plurality of my edits have been in the area of general topology, I have had many interactions with Topo over a long period of time. First, I firmly believe that he is not a troll: he means well, and most of the time he is civil, listens to others, and is amenable to reason. I also think insufferable snob misses the mark. Do remember that anyone can represent themselves any way they choose on Wikipedia. If your username is David Eppstein, it's pretty easy to confirm that there is an eminent computer scientist / mathematician named David Eppstein, and anyone who watches the contributions of User:David Eppstein can decide whether or not they think the two David Eppstein's are one and the same. (I certainly do.) Similarly, if you search on mathscinet you will find that there is a (younger) mathematician P.L. Clark, and then you can make up your own mind whether User:Plclark is that mathematician. But calling yourself "TopologyExpert" does not make it so, no more than having an expert mathematician userbox does: if you look on the list of wikipedians who self-identify in this way, you will find that there is very little overlap with the known professional mathematicians who are regularly involved with Wikiproject Mathematics. (One such self-identified expert mathematician is thirteen years old.) Let me just say that I think it is unwarranted to assume that Topo has done published/publishable research in topology and/or that he has a PhD in mathematics. To be clear, he doesn't need to have either of these qualifications to contribute to the mathematics articles on wikipedia. I just want you to realize that your appraisal that you are defending -- or even need to defend -- more venerable fields of mathematics against some mathematical elitist may not be accurate. Plclark (talk) 09:41, 21 November 2008 (UTC)
- 0 I'm afraid to say. These images are simply icons, with a vanishingly small information content. They lie more in the realm of graphic design than mathematics, attempting to convey to much information in a small space is doomed. I see no compelling reason why we need an image at all. The wording This geometry-related article is a stub. You can help Wikipedia by expanding it conveys all the essential information, any icon just serves as visual clutter. To be awkward I've removed the image entirely. Does this do the job? --Salix (talk): 00:09, 21 November 2008 (UTC)
- I don't think removing the images is a good idea. The problem is that without an image, it's not instantly obvious that the wording of the template isn't part of the article. Also the images serve a useful function by making the stub types easily distinguishable from one another. --Trovatore (talk) 01:02, 21 November 2008 (UTC)
- I am a serious mathematician and I am sorry if what I wrote was wrong. But, mathematics is such a diverse subject, that there are probably fields that you have never heard of (I know algebraists who have never heard of category theory (!)). So you have no right to insult me for what I said (and say that I am not a serious mathematician because you don't know who I am). And anyway, the stub template should be about all forms of geometry, not just Euclidean geometry which I can safely say is the least popular form (to tell you the truth, I hate Euclidean geometry but I never ever said (or dreamt) that it was not interesting).
Topology Expert (talk) 02:13, 21 November 2008 (UTC)
- Anyway, to get to the point (and stop personal attacks for not good reason), the 'connected sum' image can be made less microscopic:
But isn't it better compared to the image of the dodecahedron?
Topology Expert (talk) 02:19, 21 November 2008 (UTC)
By the way, metric geometry and Euclidean geometry are different fields. What you cited was a result at their intersection. I have not read the proof, but does it use the Euclidean metric?
Topology Expert (talk) 02:22, 21 November 2008 (UTC)
0 The dodecahedron is good because it is visible (unlike the other proposed image) and immediately conveys "geometry" to even a non-mathematician. siℓℓy rabbit (talk) 02:28, 21 November 2008 (UTC)
- As well as having a stub sorting category for category theory, we have another one for topology: {{topology-stub}}. Why do you think the connected sum image is more geometric than topological? —David Eppstein (talk) 02:48, 21 November 2008 (UTC)
- And a very nice image it is too I think. If it ain't broke don't fix it is my motto, though there are editors out there who can make tings look much more polished. As to the geometry one I vote for he dodecahedron. I like origami too and the mathematics of paper folding is modern geometry in the sense of Euclid. I must have a go at that article, I wonder where it should really go in the maths empire as it has some quite useful applications for things like airbags and dishes in space. Dmcq (talk) 10:26, 21 November 2008 (UTC)
I have indeed made mistakes in the past, but so have quite a few people in this discussion (I can't think of anyone who has not made mistakes; take Cauchy for instance. He thought that every separately continuous function was continuous and yet he is such a famous mathematician). I also think that many people would make the occasional mistake, at least, if they did not have access to much (if any) 'mathematics information'.
I learn mathematics by thinking (by working out results on my own and just reading the bare minimum of the definitions). Therefore, I make mistakes sometimes and of course, I may have some misconceptions. Even now, I make mistakes (now and then) but hopefully this should not be seen as vandalizing. I can also safely say that the field I know best is topology (but I know other fields reasonably well too) (believe it or not, I can prove many topology theorems on my own (including published ones such as Urysohn's lemma (no hints whatsoever)). I don't mean to boast, but I am just defending myself from people who think they are 'better' because they have higher qualifications. By 'topology expert' I do not claim to be better than everyone anyway. Even though you may not know my real name either, if you did, you would get quite a few (respected) results on the internet if you searched it up; plus I have been on television (thought this is irrelevant, at least it illustrates that I have some credentials). Since you already suspect it, I might as well admit that I am nowhere near a first year student but that does not say that I may not know graduate maths. I also hope that I am not judged because of this; if so, Wikipedia is discriminatory. Users such as User:Hans Adler and User:David Eppstein may be famous but that should not mean that they can attack annonymous users. I appreciate that some users don't consider themselves better because of their credentials (User:Plclark, Silly rabbit and many other such editors in this discussion for instance) and even silly rabbit: he does not give his real name but I certainly do not doubt that he knows maths very well.
One more point. Apart from a textbook on topology, I don't have many mathematics resources. Therefore, to learn maths, I am inclined to learn the necessary definitions from Wikipedia (then I can think about these definitions for years!). This has led me to start editing Wikipedia. Every single person has the right to learn mathematics. I mean, I can buy textbooks if necessary, but why not take advantage of a free encyclopedia such as this one. If I thought I was so clever, I would not spend time editing Wikipedia and furthermore, I always defend Wikipedia (you'd be amazed at the number of people who think Wikipedia is rubbish). In fact editing Wikipedia also helps me to learn; I read an article on a concept (say if I was learning what a topology was) and I change any incorrect statements based on the definition. This is a really efficient way of learning and furthermore, Wikipedia has imbedded in it the opinions of many mathematicians which is very good. This also explains why I am not a fan of references; most of the things I add to Wikipedia are from my head (even theorems and results but after hearing about WP:OR, I stopped this).
Think whatever you like of me but just because I maybe younger than you (and high-school students) does not mean that I cannot have the same credentials (you can't say that it is impossible for a 13-year old to publish something let alone a first year student). In fact, I have almost done so.
Topology Expert (talk) 13:08, 21 November 2008 (UTC)
- Three things immediately come to mind.
- I haven't reviewed your edits, so I can't comment on the apparent depth of your mathematical knowledge (and even if I had reviewed your edits, I'd likely be in too deep to comment). However, if you really are younger than a high school student, let me be first to say I'm impressed by your breadth of mathematical knowledge. Wow.
- No-one here has knocked back an idea with the reason "I have x,y and z qualifications, therefore I'm right". Everyone has offered sensible arguments for or against something. On the other hand, you have argued, several times, that peoples qualifications or knowledge should count for something. Since you feel you've been on the receiving end of this sort of argument now, perhaps you can see that it isn't a reasonable argument to use here. The argument "I know more" isn't nice, doesn't change any facts, and in matters of opinion (like the choice of a stub picture) can be totally irrelevant.
- As you pointed out, everyone makes mistakes. Tying in with your praise for Wikipedia (of which I totally agree with), one of its many advantages is that mistakes can easily be fixed by many other editors, so they're not the end of the world. Another one of Wikipedia's big positives are place like this WikiProject. There are many like minded people that can help develop solutions and form a consensus on any issues needing attention. When that happens, especially with matters of opinion, consensus should be your guiding star. The algebra stub discussion above takes up half this page now, and honestly, lived way past its consensus use-by date. You may not agree with the consensus, but ignoring it just exasperates people and, here's the important bit, still doesn't get you what you want. I appreciate your efforts though, so don't feel too bummed about it. Cheers, Ben (talk) 13:51, 21 November 2008 (UTC)
Well, I don't really want people to think me any differently knowing that I am younger than a high-school student. I just wanted to illustrate that someone can know maths even without having a PhD. I guess sooner or later people would have found out (not being a fan of references is an indicator).
I guess we should forget about the algebra stub template discussion (and I will leave them alone) so we can get back to normal editing. I suggested a circle though... (revert if you think it is not good (no need for voting)). I am currently looking to improve locally connected space and fibre bundle (an article especially in the need on attention). Perhaps knowledgeable users can contribute?
I can go by the fact that I shouldn't meddle in number theory for instance because I don't know anything about it. That's what I meant when I argued about qualifications and knowledge.
Topology Expert (talk) 14:14, 21 November 2008 (UTC)
- Don't worry, people sometimes get het up. And no I prefer the dodecahedron as it would stand out better whereas a circle can mean anything to anybody. What have you against it? Personally I rather like having books, though I go more for the pretty ones or ones which are nicely written than for the maths :) One of my favourites which mightn't be so well known is 'A Topological Picturebook' by George K Francis (1987) Springer. That sets the bar for what illustrations could be like on WP. (I just had a look at amazon, $160 for a new one but a reasonable price for secondhand. I'm sure I never paid anything like that) Dmcq (talk) 14:25, 21 November 2008 (UTC)
- Just a short note that I, too agree with Ben's "wow", and I would be very sorry if you stopped contributing. (And of course I am not famous.) --Hans Adler (talk) 00:38, 22 November 2008 (UTC)
- It should not matter whether someone is famous anyhow (there are certainly great mathematicians who were not widely known: Galois for instance). I think the voting might as well be closed by now because the dodecahedron is most favored and anyhow the dodecahedron is still the image. What I did have against the dodecahedron was that it was not as representative compared to the 'connected sum' image. Maybe the other reasons is because I prefer differential geometry compared to Euclidean (isn't differential geometry the more important theme of research (not that Euclidean geometry is not important)?). By the way, have a look at the current algebra stub template; I think that it is good but it would be better to make sure.
Oh, and just something that might interest you (User:Dmcq is that the second edition of Counterexamples in topology costs less than $10 so you might as well buy a copy.
Topology Expert (talk) 00:59, 22 November 2008 (UTC)
P.S Just to note there is a at least one field medalist who contributes to Wikipedia.
- Thanks for mentioning the current price of CiT. Ordered. --Hans Adler (talk) 11:44, 23 November 2008 (UTC)
- I've known of one of those for about three-and-a-half years. But is there only one? Many contributors don't use their real names, so can we be sure? Michael Hardy (talk) 03:55, 22 November 2008 (UTC)
Does that make it better? Is the one you know a mathematician (if you look at the Wikipedia:Wikipedians with articles page, one is listed)? As I know Oded Schramm also could have probably won a fields medal (if he was younger) but that's just for interest.
Topology Expert (talk) 03:59, 22 November 2008 (UTC)
- Please let us not speculate on how many Fields medallists or other famous people contribute and who they are. I'm intrigued by that question just like anybody else, but some people want to contribute anonymously and it is long-standing policy on Wikipedia that we respect this. -- Jitse Niesen (talk) 12:01, 22 November 2008 (UTC)
- Amen to that. And like the sheep joke lets just be content knowing that a least contributor who looked like a Fields medallist at one time contributed to Wikipedia :) Dmcq (talk)
- I don't want to speculate but the discussion came up anyhow. It is also possible to find the idenitities of annonymous editors through tedious searching but I can't be bothered to do it anymore (2, I have found out; 1 has a fields medal!).
Topology Expert (talk) 01:04, 23 November 2008 (UTC)
On the note of content, I do hate people tracking down my edits (most of the time not finding any mistakes but then exaggerating one mistake in a few months to at least some being problematic). But they will soon get tired of it when no mistakes come up.
Topology Expert (talk) 01:04, 23 November 2008 (UTC)
I am not sure if this discussion is still active, but I think that the current geometry stub template picture, Template:Geometry-stub is perfectly fine and is much better than the connected sum picture. The connected sum is fundamentally a topological rather than a geometric concept so it is not really appropriate for a geometry stub template. Connected sum might be a topology template candidate, but again I think that the current picture of the Klein bottle used in Template:Topology-stub is perfectly fine and does not need to be replaced. Nsk92 (talk) 01:19, 23 November 2008 (UTC)
My reply to User:Nsk92: The connected sum has several applications in the theory of fibre bundles. OK, perhaps the definition of the connected sum is topological. But what is the purpose of the connected sum? The connected sum is 'geometrical' because it has a lot of applications in differential geometry.
Topology Expert (talk) 03:13, 23 November 2008 (UTC)
- The question about the "purpose" of a definition is essentially meaningless. But some of the main uses of this notion occur in low-dimensional topology for constructing new (topological) manifolds out of existing ones. E.g. in 3-manifold topology one of the main notions is that of an irreducible 3-manifold, based on connected sums over spheres. There is also a version of a connected sum over tori that leads to the fundamentally important notion of a JSJ decomposition. These constructions are purely topological and their main purpose, if you will, is to break a topological manifold into simpler pieces that are easier to study. Moreover, the very definition of a connected sum is purely topological. For example, in the case of two Riemannian manifolds there is no natural notion of a connected sum as a Riemannian manifold. To say that the notion of connected sum is geometric because it has applications in geometry is nonsensical. So do lots of other purely topological notions, such as fundamental groups, covering spaces, homology and homotopy groups, spectral sequences, etc. Nsk92 (talk) 03:28, 23 November 2008 (UTC)
- I know quite a bit about the connected sum but here is an example contradicting your 'claim': The definition of a manifold is purely topological and yet it applies in differential geometry (after you equip it with a differential structure which in my mind is still topological (continuity is to topology as differentiability is to differential topology which is still topology)).—Preceding unsigned comment added by Topology Expert (talk • contribs)
- Say what? Which 'claim' of mine are you contradicting? Seems to me like a fairly pointless discussion about dictionary definitions. The notion of a topological manifold is topological, the notion of a Riemannian manifold is geometric. The notion of a smooth manifold is somewhere in between but I would certainly not put it forward as an illustrative example of a geometric notion. Truly geometric notions do have to have something to do with things like distances and angles. Nsk92 (talk) 05:56, 23 November 2008 (UTC)
- I know quite a bit about the connected sum but here is an example contradicting your 'claim': The definition of a manifold is purely topological and yet it applies in differential geometry (after you equip it with a differential structure which in my mind is still topological (continuity is to topology as differentiability is to differential topology which is still topology)).—Preceding unsigned comment added by Topology Expert (talk • contribs)
Distances and angles, only??? Manifolds are used mostly for geometry. I am not saying manifolds have nothing to do with topology (they are of course important in this field) but which topic are they most used in (Riemannian geometry as you mentioned is a subfield of geometry)?
Topology Expert (talk) 07:24, 23 November 2008 (UTC)
- Oh, please, this is getting absurd. It is not where the notion is "used" but the nature of the definition of a particular notion that defines whether or not the notion is topological, algebraic, geometric or whatever. Covering spaces are mostly used to study manifolds (according to you a geometric notion), but that does not make the notion of a covering space geometric. Most applications of groups are probably geomertric (as is the main motivation of the definition by considering groups of symmetries), but the notion of a group is certainly algebraic. Nsk92 (talk) 12:12, 23 November 2008 (UTC)
- Yes but the notion of angles and distance is in usually seen as the point where topology ends and geometry begins. In fact, the working definition for topological for physicists is approximately, "being independent of any metric." (i.e. a topological field theory is one which does not depend on the choice of metric.) Of course, there are many reasons why this view is somewhat wrong from a purely mathematical perspective, but it shows how important distances and angles are for what people view as geometry.
- I also don't quite follow your logic. Manifolds are mostly used in Riemannian geometry so they must geometrical. Consequently, the connected sum, which makes no sense for Riemannian manifolds, but is applied to manifolds must be a fine example of geometry. Say what?
- Geometry = distance and angles? Algebraic geometry has none such. Ryan Reich (talk) 17:51, 23 November 2008 (UTC)
- Actually, I happen to think (as I know do many others) that "algebraic geometry" as a term is a bit of a misnomer, although, of course, the name by now is very well established. The connections with geometry, as most mathematicians would think of it, are rather tenuous, and I believe that most mathemnaticians view algebraic geometry as essentially a part of algebra rather than of geometry (or at least as being much closer to algebra than to geometry). That is certainly the case in my department where algebraic geometry has historically always been a part of the algrebra research group. There are, of course, strong connections with geometry proper there, especially of historical nature, particularly with Riemann surfaces (definitely a geometric concept). In fact, anything to do with conformal maps (preservation of angles) does have a strong geometric flavor, IMO. Nsk92 (talk) 18:12, 23 November 2008 (UTC)
- Geometry = distance and angles? Algebraic geometry has none such. Ryan Reich (talk) 17:51, 23 November 2008 (UTC)
- I had a big response prepared, but since I don't want to do what Topology Expert is doing in these conversations, I will pass on it. Instead, let me just say that from my perspective, geometry uses everything starting from topology and up to and including metric properties, but is more of a scale; on this scale, algebraic geometry is a sort of absolute geometry that studies properties not requiring the use of a metric or other particular marking device (like a symplectic form, for example). In addition to its foundations, that makes it more algebraic than Riemannian geometry, for example, is, because the focus is on incidences, relationships, and configurations, rather than on measurement. The foundations itself require that the subject essentially be practiced as algebra, but that doesn't mean that it is algebra any more than algebra phrased with commutative diagrams is category theory (or category theory is algebra, despite its basic objects being a generalization of many algebraic structures). Ryan Reich (talk) 20:29, 23 November 2008 (UTC)
- Topology Expert: you say that a definition is "geometric" if despite being based on purely topological ideas, it finds its important uses in geometry. Mathematically, whatever; but since this is ostensibly a discussion about the geometry stub icon, I want to draw attention to the fact that this distinction (domain of definition versus domain of application) is precisely the one you were making in the algebra stub section, and embodies the same misconception you displayed there about the use of the icon itself. Its contents should say "geometry" as much as the words next to it; it shouldn't require a sophisticated understanding of the use of the object depicted, as well as perhaps a knack for reading your mind, to figure out that the picture really is about geometry. It shouldn't have to be the picture that represents the thousand words of argument you are making to support it. Ryan Reich (talk) 17:51, 23 November 2008 (UTC)
The article, geometry is getting vandalized (more than twice every day) by idiots who have nothing better to do than vandalize. Can't we do something about it? For at least the whole time the article existed, most edits are either:
a) Vandalizm
b) Reverting vandalizm
Something has to be done. I would suggest:
a) Semi-protect the article (more important)
b) Block vandalizers for a day for any vandalizm; increase this block to a week, then a month etc.. until an indefinite block if abuse is repeated. I think that vandalizers are dealt with too lightly on Wikipedia.
But since I am not an admin, I would leave the decisions to a real one.
Topology Expert (talk) 07:33, 23 November 2008 (UTC)
- In general I prefer to avoid (semi) protection as it can block of some helpful edits. However there have been few such edits in recent time so I've semi-protected it for a month (see WP:SEMI). --Salix (talk): 08:08, 23 November 2008 (UTC)
- You can always ask for help at Wikipedia:Requests for page protection. Unfortunately, policy is strongly tilted against protection, especially lengthy protection. JRSpriggs (talk) 21:14, 23 November 2008 (UTC)
Logical connective[edit]
A single-purpose account User:Boolean hexadecimal, proposes replacing a large amount of text in tables with a large imagemap (so that the text is replace by an image of text). The image is not only less clear than the tables, it's awful for accessibility. Could someone else look into this? — Carl (CBM · talk) 20:56, 18 November 2008 (UTC)
- It looks like he did that to the German equivalents is trying to update the English version to the same, his German account is de:Benutzer:Boolean hexadecimal. I think it's probably just a question of somebody pointing out the problems and saying the information needs to be accessible.
- As a matter of interest on accessibility - how would a blind person get access to the formulae displayed using <math> on WP, is there something about that somewhere? Dmcq (talk) 10:47, 19 November 2008 (UTC)
- This isn't the first time he's done this. Although I remember his gigantic imagemap being orange instead of blue. —Dominus 14:21, 19 November 2008 (UTC)
- Here. —Dominus 14:23, 19 November 2008 (UTC)
- I had a good look at it and decided even if it was good I would be against it. The reason is that it would lock out other editors. We should try as far as possible I feel make contributions such that someone good at the subject can contribute - not have people versed in html make things difficult for them. Dmcq (talk) 19:58, 19 November 2008 (UTC)
- Here. —Dominus 14:23, 19 November 2008 (UTC)
 |
 | |
Hi,
what I like about the representation above is the following:
- When I touch the nibbles in the table, they are explained to me bit by bit. Please do not underestimate, that this can be helpful for people, who do not already know the subject.
- The tesseract shadow Hasse diagram shows all possible deductions. The Venn diagrams are helpful representations, of what the connectives actually mean or do. When I touch the odd bit connectives in the diagram, I can see that the 1 bit connectives are conjunctions and the 3 bit connectives are disjunctions (without cropping the article with text about details like this).
- Last but not least: I like the silver Thue-Morse sequence in the table, and the silver cube in the diagram. (These are interesting links to other regions of mathematics, and could even be mentioned in a "see also" section at the end of the article.)

Concerning accessibility:
It is true, that articles should also be accessible to blind people, and for plain text uses, may it be for wapedia or whatever. I take that very serious. But in these cases a table containing wikipedia math symbols would be not useful as well. Thus a good solution for all kinds of users is to keep the imagemap template in the article, and to add a note like this: "Here you find this information in plain text."
The lines in this table should simply look like this:
- (P AND Q) = (P material nonimplication not Q) = (not P converse nonimplication Q) = (not P NOR not Q) = 0001
The information displayed in the Hasse diagram can be shown by a simple list of conclusions like these:
- If the statement "Q" is true, the statements "P OR Q" and "P material implication Q" are also true.
I can create this subpage Logical connectives text table, if you agree that it makes sense. I think it does.
Greetings, Boolean hexadecimal (talk) 12:19, 26 November 2008 (UTC)
- I'm going to copy this to Talk:Logical connective and respond there. — Carl (CBM · talk) 13:26, 26 November 2008 (UTC)
LaTeX bug[edit]
As many people here are probably aware, there is apparently a bug causing LaTeX formulas to no longer appear. It seems like texvc refuses to regenerate pngs, like it doesn't know that the previously cached images are no longer available. This has happened before, but it was always fixed within hours of the problem appearing. The problem now has been ongoing for several days. Does anyone here know if the devs are aware of this problem? If so, is some effort being made to fix the problem? How long should we expect this to continue? siℓℓy rabbit (talk) 13:55, 23 November 2008 (UTC)
- JRSpriggs noted in Strange software bug above that if you add "?action=purge" to the URL of the page that has a dodgy picture, it fixes it. I tried that on one page, but it didn't seem to work. I went back to the page a day or so later and the dodgy pic was fixed. So either I don't understand JRSpriggs' instructions, and someone else fixed it, or it just takes a little while to fix. Cheers, Ben (talk) 14:01, 23 November 2008 (UTC)
- Purging only works if the bad image has been deleted (which can't be done manually without server access). The fix that works is to alter the code (adding a superfluous pair of braces to the end works, for example). The devs certainly should be aware of the problem, given the number of times it's been on WP:VPT, but I can't find any definite statement to this effect, nor can I find the bug on bugzilla. Algebraist 14:05, 23 November 2008 (UTC)
- I just filed it as bugzilla:16440. The devs have been aware of this for some time (I keep asking them to delete empty images one at a time) but they have no idea what's causing the problem. — Carl (CBM · talk) 14:25, 23 November 2008 (UTC)
- Thanks Carl. siℓℓy rabbit (talk) 21:11, 23 November 2008 (UTC)
- Purging only works if the bad image has been deleted (which can't be done manually without server access). The fix that works is to alter the code (adding a superfluous pair of braces to the end works, for example). The devs certainly should be aware of the problem, given the number of times it's been on WP:VPT, but I can't find any definite statement to this effect, nor can I find the bug on bugzilla. Algebraist 14:05, 23 November 2008 (UTC)
I'm finding yet another instance in golden ratio just below the words "Number of the Beast". Two lines of unrendered TeX code. Purging hasn't helped. Michael Hardy (talk) 20:08, 24 November 2008 (UTC)
I don't believe purging helps. Last time I checked, was not working either. — Carl (CBM · talk) 00:25, 25 November 2008 (UTC)
- Another one: At radius of convergence, two lines into the "Definition" section. Purging didn't help. I emailed Brion Vibber about this. He's Wikipedia's only salaried software expert. No answer yet (more than 24 hours later). I think we need to compile a list of cases whenever we find them, lest anyone think this is not an urgent problem. Michael Hardy (talk) 01:21, 26 November 2008 (UTC)
- ...OK, I edited that one and it's working now. But purging and reloading didn't help, so there's a problem. Michael Hardy (talk) 01:24, 26 November 2008 (UTC)
- OK, now I've returned the code to the way it was, exactly like this:
- f(z) = \sum_{n=0}^\infty c_n (z-a)^n,
- and the bug is back: it's not rendering. Michael Hardy (talk) 01:26, 26 November 2008 (UTC)
- OK, now I've returned the code to the way it was, exactly like this:
- Ok, 0-byte math PNGs are now deleted and re-rendered, and old versions will be purged from the proxy cached on re-rendering. (You might still need a client reload sometimes.) --brion (talk) 02:39, 26 November 2008 (UTC)
Thank you, Brion. Michael Hardy (talk) 03:27, 26 November 2008 (UTC)
- still doesn't work. —Bkell (talk) 16:49, 26 November 2008 (UTC)
- It does for me (with 'Always render PNG' set). Have you cleared your browser cache? Algebraist 16:52, 26 November 2008 (UTC)
- Yes, I reloaded, cleared my cache, etc. It is working now—I assume someone has fixed it. Here's another: . —Bkell (talk) 17:12, 26 November 2008 (UTC)
- Also fine here after purge and bypass. Algebraist 17:15, 26 November 2008 (UTC)
- What do you mean by "purge and bypass"? —Bkell (talk) 17:16, 26 November 2008 (UTC)
- WP:PURGE, WP:BYPASS. Algebraist 17:19, 26 November 2008 (UTC)
- Okay, I have purged articles containing the image, cleared my cache, loaded the image separately in a new tab and reloaded. None of those seem to have any effect. I have tried downloading the image with cURL, and I get a zero-byte file. Now and work for me (after you posted replies), but still doesn't (even after your reply), and neither do . —Bkell (talk) 17:43, 26 November 2008 (UTC)
- That's odd. I've just purged this page, and now those images are fine. Algebraist 17:46, 26 November 2008 (UTC)
- Okay, I have purged articles containing the image, cleared my cache, loaded the image separately in a new tab and reloaded. None of those seem to have any effect. I have tried downloading the image with cURL, and I get a zero-byte file. Now and work for me (after you posted replies), but still doesn't (even after your reply), and neither do . —Bkell (talk) 17:43, 26 November 2008 (UTC)
- WP:PURGE, WP:BYPASS. Algebraist 17:19, 26 November 2008 (UTC)
- What do you mean by "purge and bypass"? —Bkell (talk) 17:16, 26 November 2008 (UTC)
- Also fine here after purge and bypass. Algebraist 17:15, 26 November 2008 (UTC)
- Yes, I reloaded, cleared my cache, etc. It is working now—I assume someone has fixed it. Here's another: . —Bkell (talk) 17:12, 26 November 2008 (UTC)
Overhaul of assessment and project banner[edit]
Looking at the assessment and categorisation of mathematics articles it seems to me that many improvements can be made and this WikiProject can be brought more into line with other projects. There could be several advantages to this.
- When new people join the project they are more likely to understand how things work if they have worked with other WikiProjects.
- As procedures evolve general in Wikipedia, there is less to do to keep our procedures up to date: by standardising, it is easier to keep individual projects up to date.
My main proposal is that we convert the project banner {{maths rating}} to use the standard meta-banner Template:WPBannerMeta. I have done quite a bit of work on this and the result is currently at Template:WikiProject Mathematics. It does not look exactly the same as the current one - I've got some examples to show you below. Other proposals are:
Other proposals[edit]
- Move categories Top/High/Mid/Low-Priority mathematics articles to Top/High/Mid/Low-Importance mathematics articles
Create categories on fields, i.e. Articles on Number theory/Discrete mathematics/Analysis/... with parent category Category:Mathematics articles by field.Struck because it would be duplication of categorisation of the article.- As B+ is not a standard class I suggest the following. Make B+ class articles a subset of B-Class articles (so B+ articles will appear in both categories)
- Clear out Category:WikiProject Mathematics articles so that it contains only subcategories. (Currently contains 145 pages and looks very cluttered.
- Move the assessment criteria which appears on every category (e.g. Category:WikiProject Mathematics articles) and link to it instead. (At the moment you have to scroll down a long to see the articles which are in the category.)
Questions[edit]
- Is it better to switch to the more standard Template:WikiProject Mathematics (and redirect Template:Maths rating to this) or stick to Template:Maths rating?
- Should we implement the full quality scale, which includes categories such as Featured List (a few of which do exist in the project) and disambiguation pages, or just the standard scale (FA, A, GA, B, Start, Stub, NA)?
- Currently Bplus-class articles are also categorised as GA-class. Have all these articles been listed as good articles? If yes, they should probably be classified as GA-class. If no, they should not be categorised as such.
Examples[edit]
Please see my sandbox for various different combinations. In order to show comments it was necessary to use mainspace, so I've pasted the proposed new banner on the following pages to demonstrate:
I will take personal responsibility to ensure that any changes work as desired and any teething problems are fixed. Your thoughts please? MSGJ 20:48, 17 November 2008 (UTC)
Discussion[edit]
- While the project in general makes some sense, I don't agree with changing Priority to Importance. The point is that these ratings are supposed to be a ranking of the priority assigned to improving the article, according to how it will affect the way users perceive the quality of the corpus of mathematical articles. Therefore more basic articles have higher priority; that makes sense to expert editors. You'll have a lot harder time convincing them that the basic subjects are more important than the shiny and sexy, but extremely specialized and technical, articles that they'd really prefer to work on. --Trovatore (talk) 21:11, 17 November 2008 (UTC)
- I take your point. But you could just think about it as being more important to work on particular articles at a particular time, rather than the actual subjects being more important than others. MSGJ 22:02, 17 November 2008 (UTC)
- Well, you could, but is that what people will do? Personally I would be offended to see a "low-importance" tag on pointclass -- it's an extraordinarily important topic. Just wouldn't go down my gullet, even with the explanation (and not everyone will know the explanation). But I can live with low-priority. I suppose.
- Frankly the better solution, if uniformity is desired here, would be to change it to "priority" everywhere else. This is a case where the math project has it right. --Trovatore (talk) 22:16, 17 November 2008 (UTC)
- I tend to agree with you in principle. I'm not sure if it's worth going against the overwhelming majority on this one. I notice that WikiProject Biography use "priority" and some other small projects like WikiProject British Royalty and Wikipedia:WikiProject Video games, but less than a dozen in total. MSGJ 09:46, 18 November 2008 (UTC)
- I take your point. But you could just think about it as being more important to work on particular articles at a particular time, rather than the actual subjects being more important than others. MSGJ 22:02, 17 November 2008 (UTC)
- Well, if it's a choice between following the majority on this or continuing to have our own convention, I say we go with our own convention. Uniformity has some value, but not that much. We can drop a hint in other projects' ear from time to time. --Trovatore (talk) 10:06, 18 November 2008 (UTC)
- It's funny that WikiProject Mathematics/Wikipedia 1.0/Assessment category format talks about importance more than priority. We also have Category:Mathematics articles by importance and Category:Unassessed importance mathematics articles. Seems we are confused! I have updated the banner to use the word priority instead of importance but we should decide which one we are going with. (And I still suggest we stick with the majority ...) MSGJ 12:04, 18 November 2008 (UTC)
- I thought that the categories were still named "by importance" because the WP 1.0 bot required it. However, I looked at the code and it looks like it should be fine with "by priority" instead. I never worried about it before because the categories are really only for the bot, so they can have strange names and only the bot operators need to worry about it. But I agree with Trovatore that "priority" is a more neutral term than "importance". The vast majority of our articles are Low-priority, but this in no way means they are of low importance. — Carl (CBM · talk) 13:19, 18 November 2008 (UTC)
- It's funny that WikiProject Mathematics/Wikipedia 1.0/Assessment category format talks about importance more than priority. We also have Category:Mathematics articles by importance and Category:Unassessed importance mathematics articles. Seems we are confused! I have updated the banner to use the word priority instead of importance but we should decide which one we are going with. (And I still suggest we stick with the majority ...) MSGJ 12:04, 18 November 2008 (UTC)
- Well, if it's a choice between following the majority on this or continuing to have our own convention, I say we go with our own convention. Uniformity has some value, but not that much. We can drop a hint in other projects' ear from time to time. --Trovatore (talk) 10:06, 18 November 2008 (UTC)
Well that's one thing that seems to be decided then (stick with Priority over Importance). Does anyone have any answers to my three questions? MSGJ 07:03, 19 November 2008 (UTC)
- 1. and 2. I personally don't feel the need to change anything there. 3: As far as I understand, the levels are more or less the same, but I think any article can be only either B+ or GA. The difference is that GA needs a review by somebody, whereas you can give B+ status yourself. Insofar I think it's good to have the two. Jakob.scholbach (talk) 10:01, 19 November 2008 (UTC)
Bplus class[edit]
The new template does not "categorize" Bplus articles as B articles – it completely replaces the Bplus class with B class. So there would be no more Bplus articles at all. In the past there has been support for keeping the Bplus rating. What do people thing now? — Carl (CBM · talk) 14:18, 20 November 2008 (UTC)
- This isn't true actually. The template is still populating Category:Bplus-Class mathematics articles. Bplus articles are now regarded as a subset of B-Class articles, so they will appear in both categories. We could make Category:Bplus-Class mathematics articles a subcategory of Category:B-Class mathematics articles articles to reflect this. MSGJ 14:22, 20 November 2008 (UTC)
- Traditionally Bplus articles have been treated as a subset of GA articles; this is more accurate in terms of quality.
- When the new WP 1.0 bot comes out (it's in development), it will explicitly support projects that have nonstandard ratings like this. So at that point the template will need to assign these articles to Bplus class and not at all to B class. I'm not sure how to achieve that with the new template; I don't think the NOTE_1 technique will work. I suppose at that point we can subst the WPBannerMeta template and fix the local copy. — Carl (CBM · talk) 15:58, 20 November 2008 (UTC)
- Or we could nominate all the Bplus articles for good articleship and do away with the Bplus class. MSGJ 16:31, 20 November 2008 (UTC)
- As I mentioned earlier, "good article" means a specific thing: articles which have been nominated and listed through the WP:Good articles process. I do not think it is appropriate to categorise articles as GA-Class when they are not good articles. MSGJ 17:11, 20 November 2008 (UTC)
- The only reason for the duplication at all is that the current WP 1.0 bot doesn't know how to handle Bplus. I agree this isn't ideal; that's why the next version of the WP 1.0 bot will handle the Bplus rating correctly. But the Bplus ones have been in the GA category for a long time, and I don't think there's a good reason to switch them to the B category. The table compiled by VeblenBot does give the correct numbers for Ga/Bplus/B, it's only the WP 1.0 bot table that is wrong. — Carl (CBM · talk) 17:44, 20 November 2008 (UTC)
- I did give a reason not to use the GA category and it seems an important one to me. I don't know much about the similarities between B+ and GA, but I know GA reviews are very thorough and because the reviewer of a GA nominee is not someone who has been involved with editing the article, I suspect that GA status is possibly more meaningful. (There is nothing to stop the author of an article giving it B+ class, is it?) Carl, with respect, your arguments do seem to revolve around "this is the way we've always done it so why should we change?". If you have a look at Talk:Gottfried Leibniz you can see how ridiculous the current situation is: every project classifies it as B-class except mathematics which classifies it as GA-class. It's okay to be different from other projects but we can't be this different. MSGJ 06:00, 21 November 2008 (UTC)
- The only reason for the duplication at all is that the current WP 1.0 bot doesn't know how to handle Bplus. I agree this isn't ideal; that's why the next version of the WP 1.0 bot will handle the Bplus rating correctly. But the Bplus ones have been in the GA category for a long time, and I don't think there's a good reason to switch them to the B category. The table compiled by VeblenBot does give the correct numbers for Ga/Bplus/B, it's only the WP 1.0 bot table that is wrong. — Carl (CBM · talk) 17:44, 20 November 2008 (UTC)
- When the new WP 1.0 bot comes out (it's in development), it will explicitly support projects that have nonstandard ratings like this. So at that point the template will need to assign these articles to Bplus class and not at all to B class. I'm not sure how to achieve that with the new template; I don't think the NOTE_1 technique will work. I suppose at that point we can subst the WPBannerMeta template and fix the local copy. — Carl (CBM · talk) 15:58, 20 November 2008 (UTC)
- The issue with Talk:Gottfried Leibniz is, as I said, that the new template does not actually implement B+ class. The talk page should say "Wikiproject Mathematics (B+ class)" in the ratings at the top, and also have the GA categories at the bottom. Then, when the new WP bot is finished, the GA categories at the bottom can go away, and it will just say B+ class. The only reason it says GA at the top of the talk page is that the current template has a bug. If it said "B" in the template that would be just as much a bug. That's why I started this thread.
- I don't think anyone has the time to go through the GA process for all the B+ articles, so I think the real options are:
- Fix the template so that it correctly recognizes B+ articles and does not call them either B or GA articles in the template's displayed output, or
- Stop using the B+ class
- — Carl (CBM · talk) 14:23, 21 November 2008 (UTC)
- I don't think anyone has the time to go through the GA process for all the B+ articles, so I think the real options are:
- I think the later might be best. The introduction of c-class to the quality scale sort of obsoletes part of the reason for the existence of the B+ class, namely differentiating between articles that are certainly beyond start class but still need quite some work, and those that are nearly GA-level. (TimothyRias (talk) 22:16, 21 November 2008 (UTC))
- I propose we classify them as B-Class but retain the B+ label for use within the project to tell us that the article might be a potential GA or A-class. When the bot can handle B+, and of the project still wants to use it, I am happy to write a hook for the template which will classify it as B+ and nothing else. MSGJ 10:46, 24 November 2008 (UTC)
- I am very annoyed by this unilateral intervention. Talk:Gottfried Leibniz was only classified as GA-Class because you changed the template. I have changed it back to the more compact, less error-prone version that existed before this misguided attempt to standardize against long standing consensus. Geometry guy 00:45, 25 November 2008 (UTC)
Keep B+. It serves a useful purpose. linas (talk) 04:27, 4 December 2008 (UTC)
Non-articles should not be assessed[edit]
Our longstanding consensus has been that the maths rating template is for rating math articles, not for tagging every page that is somehow related to math. Since the new banner template is quite willing to allow people to tag templates, categories, etc. with it, that's a problem. We could add a check to the template so that it only works on Talk: pages and not on other pages. It's really a pain to have to go back through and fix these after they have been mistakenly tagged by a well-intentioned editor (I know from experience). — Carl (CBM · talk) 14:20, 20 November 2008 (UTC)
- Question: by articles do you mean any page in main (article) space? Because there are various classes of articles which are in mainspace but are not counted as articles by the assessment scheme. For example, lists, featured lists, disambiguation pages, ... We should decide which of these we want to cater for and then not bother with the other categories. MSGJ 14:26, 20 November 2008 (UTC)
- Well, maybe this stand point should be re-evaluated. There are good reason for tagging non-article pages with project banners. For example it makes it a lot easier to contact the interested wikiprojects when a page is subject of discussion, for example when it is proposed for deletion.
- Also, I see very little reason not to do it. (Other than it is a lot of work to add the banners, but that is a none problem, since in the end somebody will come around and do it.) (TimothyRias (talk) 14:39, 20 November 2008 (UTC))
- We also have quite a few mathematical pictures, and it might well be useful to have these in a category together, e.g. Image-Clas Mathematics articles. MSGJ 15:24, 20 November 2008 (UTC)
- We already have a category for them: Category:Mathematics images. — Carl (CBM · talk) 16:06, 20 November 2008 (UTC)
- We also have quite a few mathematical pictures, and it might well be useful to have these in a category together, e.g. Image-Clas Mathematics articles. MSGJ 15:24, 20 November 2008 (UTC)
- Timothy: which pages are you talking about, that this project might need to be notified of their deletion? Apart from a few templates and the subpages of WP:WPM, I can't see how we'd be very interested in announcements about non-articles. It's just not a very common problem. — Carl (CBM · talk) 16:06, 20 November 2008 (UTC)
- The various mathematics templates would definitely be an example. So, are the mathematics categories and images etc. (As note to the side, WPBannerMeta also supports an option to only allow the old restricted range of classes. (TimothyRias (talk) 16:19, 20 November 2008 (UTC))
- As a general point: we already have List of mathematics articles that includes lists, featured lists, articles, etc. and does not require any talk page tags at all. It's based just on the categorization of the pages themselves. So the only added benefit of talk page tags is for article assessments. — Carl (CBM · talk) 16:06, 20 November 2008 (UTC)
- Well, actually there is also the advantage of easier maintenance. If categories are applied through a template, it is much easier to later adjust the categories, or for example create cross-category lists. I do admit that this benefits mainspace articles much more than the other articles.(TimothyRias (talk) 16:19, 20 November 2008 (UTC))
- I don't follow. In the ordinary course of editing, categories are added to the article itself, which causes the article to appear in the List of mathematics articles. No extra maintenance or effort is required, and the talk page doesn't even have to be created. — Carl (CBM · talk) 16:39, 20 November 2008 (UTC)
- I think I've just found out that lists and featured lists are included on the standard scale so my concerns are satisfied on thi for now. MSGJ 06:01, 21 November 2008 (UTC)
- I don't follow. In the ordinary course of editing, categories are added to the article itself, which causes the article to appear in the List of mathematics articles. No extra maintenance or effort is required, and the talk page doesn't even have to be created. — Carl (CBM · talk) 16:39, 20 November 2008 (UTC)
Preamble to categories by quality/importance[edit]
Regarding proposal 5 above, it seemed to me that these categories had too much information on them and were very cluttered. You needed to scroll down a long way to actually see what articles were in those categories. My proposal is to have some brief information about assessing articles and a link to a page with the full details. The more standard method is just a simple template at the top which links to the other categories (see this [[:Category:B-Class Berbers articles|example). I know a lot of work went into the WikiProject_Mathematics/Wikipedia_1.0/Assessment_category_format template and I don't intend to disparage it. But I'm wondering about the rationale of having on every single category page. MSGJ 15:10, 20 November 2008 (UTC)
- There's not a lot of reason to manually browse the category lists; there are nicely formatted lists such as
- for human consumption.
- There may have been too much text on the old template, but the general strategy of using a single template is sound. It keeps the pages in sync and makes it easier to change them all with one edit when needed. — Carl (CBM · talk) 16:01, 20 November 2008 (UTC)
- Okay, agreed. It's looking much better now. MSGJ 06:01, 21 November 2008 (UTC)
What happened to the "field" parameter?[edit]
The new template doesn't seem to do anything with the "field" parameter. Is this a bug? --Trovatore (talk) 22:11, 20 November 2008 (UTC)
- If you click the "show more information" it will tell you more information including its field. Would you like it do more than this? MSGJ 05:49, 21 November 2008 (UTC)
- Well, first of all I wouldn't hide it -- should be equal prominence with quality and importance. But didn't it also use to put the talk page in appropriate categories? Or is that done by the bot? --Trovatore (talk) 06:06, 21 November 2008 (UTC)
- I was trying to make the banner a bit smaller as it was getting quite big. But it can be easily unhid if that's what people want. No, it wasn't categorised before, but again, that could be done easily. MSGJ 06:11, 21 November 2008 (UTC)
- Well, first of all I wouldn't hide it -- should be equal prominence with quality and importance. But didn't it also use to put the talk page in appropriate categories? Or is that done by the bot? --Trovatore (talk) 06:06, 21 November 2008 (UTC)
- Do we want it to? It wouldn't be too much trouble to add to the template. (This btw is exactly what I meant by having the banner manage cats is easier on maintenance. Now adding a couple of lines to the template can apply the right category to all the maths articles that have their field defined. It is also why I said it benefits main space articles more.) (TimothyRias (talk) 21:33, 21 November 2008 (UTC))
- What should the categories be called? I've set it to Category:Geometry-field mathematics articles, Category:Mathematicians-field mathematics articles, Category:Statistics-field mathematics articles, etc. but haven't created the categories yet. MSGJ 10:40, 24 November 2008 (UTC)
- Do we want it to? It wouldn't be too much trouble to add to the template. (This btw is exactly what I meant by having the banner manage cats is easier on maintenance. Now adding a couple of lines to the template can apply the right category to all the maths articles that have their field defined. It is also why I said it benefits main space articles more.) (TimothyRias (talk) 21:33, 21 November 2008 (UTC))
C-Class articles[edit]
We have a non-empty set of Category:C-Class mathematics articles. This category does not seem to be well integrated with the rest of the WP-math system. What should be done with this category? --Salix (talk): 11:19, 24 November 2008 (UTC)
- I'll go through the list -- it's not that long. Quite a few of these can clearly be placed into the Start or B category, and I'll make some preliminary assessments. RayAYang (talk) 02:51, 25 November 2008 (UTC)
Wolfram Demonstrations Project[edit]
259 articles link to The Wolfram Demonstrations Project, which redirects to Wolfram Demonstrations Project. Could people help bypass the redirect? Michael Hardy (talk) 12:42, 1 December 2008 (UTC)
- As there were no double redirects this is not really a problem. But I have fixed 100 of them for you. Martin 13:38, 1 December 2008 (UTC)
Thank you. I'll get to some of them myself later today unless someone beats me to it. Michael Hardy (talk) 17:30, 1 December 2008 (UTC)
...I've done a dozen or so so far. Michael Hardy (talk) 21:51, 2 December 2008 (UTC)
Peer review for Locally connected space[edit]
Anyone who is interested is welcome to contribute. Any comments/feedback (however minor) will be greatly appreciated.
Thanks, Topology Expert (talk) 11:12, 20 November 2008 (UTC)
- I have just completed some major revisions of this article, roughly along the lines which were indicated both in the peer review and my own (earlier) comments on the talk page. I would be happy to receive feedback on the new version. Here is one suggestion that I have which I will not myself implement but I hope someone else does: the graphic for topologist's sine curve should be changed. The present one looks like the result of actually plotting the curve y = sin(1/x) using some software package, and this image does not in fact give a good geometric intuition of why (or even where!) the space is not locally connected. A more schematic image which zoomed in on some small open disk with center slightly to the right of x = 0 would be much more useful, I think. Plclark (talk) 09:27, 27 November 2008 (UTC)
This is more like wish list, but it would be very nice if the article discusses closed-related topics such as Locally simply connected space or Semi-locally simply connected space. Also, the examples section should contain more concrete examples, examples familiar to non-topologists, if any. (I know very little topology, so I can't edit the article myself.) By the way, I really liked the intro; compactness implies locally compactness, but connected doesn't imply locally connected. This is probably basic but conceptually important, I suppose. -- Taku (talk) 12:14, 27 November 2008 (UTC)
- I heartily agree with your request for more examples. For instance, the article currently does not give the example of an open subset of Euclidean n-space as an example of a locally connected space! In this regard, the theorem about when a product of nonempty locally connected spaces is locally connected (namely, when all factors are locally connected and all but finitely many are connected, exactly the same as for local compactness) would also be helpful. I hope to add this material in the near future. Regarding the relations with semi/local simple connectedness, the question is whether such a discussion belongs in this article, in the articles on these other topics, or both. Currently the lead mentions connectedness and local path connectedness as necessary conditions for the existence of universal covers but does not mention the additional necessary that is, jointly with the first two, sufficient: semilocal simple connectedness. I am inclined to agree with you that it would be better to explicitly mention the s.s.c. condition. Plclark (talk) 02:19, 28 November 2008 (UTC)
I am back from an unanticipated Wikibreak and I am extremely pleased with the changes made to the article. Thankyou very much to Plclark, geometry guy, Jakob and other editors for contributing. I will follow up on the comments by Jakob and geometry guy that have not yet been attended to. I will also respond more on the article's talk page but it may take until tomorrow. Just a note: after the recent changes, has the article improved to GA class?
The article mentions that an open subset of a locally connected space is locally connected and hence the same holds for Euclidean space. Plclark: your edits were very helpful but I feel that they are missing out on generality. For instance, originally I had written that an open connected subspace of a locally path connected space is path connected and now it is changed to the special case where the subspace in question is the whole space (and just an unrelated note that local path connectedness cannot be changed to local connectedness in the hypothesis of the theorem as a countable set given the cofinite topology shows; maybe this example could be added). I had earlier written that any linear continuum is locally connected and connected and now it is just restricted to R. I prefer generality rather than examples (prove that a weakly locally connected space is locally connected and then there should be no need to prove this for a particular weakly locally connected space). Anyway, this can be fixed (it will take sometime though) but until then, perhaps editors should stick to being general.
Thanks again.
Topology Expert (talk) 15:25, 4 December 2008 (UTC)
User:JRSpriggs is attempting to sway a deletion process with Personal attack on physics project page[edit]
User:JRSpriggs is attempting to sway a deletion process with Personal attack on physics project page. I removed the comment, but he reinserted it. Comment was added here: [4] and removed here: [5] and then reinserted here: [6]. Delaszk (talk) 11:13, 28 November 2008 (UTC)
- I added a comment there that JRSpriggs's wording is too strong and suggested that he edited it. Nevertheless, I can understand his frustration. I think you should take more notice of what other editors say instead of trying to push through your understanding of relativity which is very likely to be misguided from what I have seen. -- Jitse Niesen (talk) 11:50, 28 November 2008 (UTC)
- My first edits on special relativity a few weeks ago were misleading and they have been deleted. I have taken notice of what they said and my more recent edits on the topic have reflected that.
- But this issue is about the article de Sitter invariant theories (previously titled de Sitter relativity) under deletion discussion. The quality of some of the edits I have previously made is not pertinent to the question of notability of the topic google hits for de Sitter invariant. If JRSpriggs has anything to say about that topic he should say it on the AfD page. JRSpriggs has indulged in a pattern of inflammatory language about this from the beginning. Prior to this AfD our last encounter was a discussion in which he argued against time measured in metres and then gave up when he realized that time in metres is possible. But that's no reason to abandon that time-in-metres discussion and then wait for an opportunity to sabotage an article I created. Delaszk (talk) 12:31, 28 November 2008 (UTC)
- Ummm ... this is the talk page for WikiProject Mathematics, and I don't see how this complaint is remotely relevant here. We have dispute resolution procedures for this stuff. First step is to discuss with the editor concerned; possible escalation includes posting to WP:ANI, which I see you have already done. Posting here as well doesn't help your case because it looks like forum shopping. Also - do you really want to publicise the fact that you went to DEFCON 3 over the word "crank" ?? Gandalf61 (talk) 14:01, 28 November 2008 (UTC)
The article has now been deleted, but a Deletion review has been opened. Comments welcome. Geometry guy 21:19, 29 November 2008 (UTC)
This is not the only time that User:JRSpriggs has made a (false) personal attack to hide his misunderstanding/incompetence. See this and notice that JRSpriggs undid that edit because of his lack of knowledge (he did not even bother to read that section to see the counterexample mentioned as silly rabbit pointed out).
Topology Expert (talk) 18:00, 4 December 2008 (UTC)
- To Topology Expert: My main point was that the two sections you added to Countable set were out of place in that article. I still believe that they were too far off the topic.
- I was confused by the line "Before proving this, we give some examples:" in one of the two sections, which was followed by an explanation of why the conditions in the hypothesis of your theorem were necessary. So I misinterpreted your explanation as something which it was not. Naturally, so interpreted, it made no sense. I apologize for misinterpreting it and thus jumping to the false conclusion that there was an error in the section. JRSpriggs (talk) 04:48, 5 December 2008 (UTC)
Thankyou for the apology but this is just my explanation as to why the placing was correct:
Topology and set theory are so closely linked that they are practically the same subject except for the fact that in topology you analyse a collection of sets satisfying certain axioms rather than analysing sets in general. So really, it would be strange for there to be no topology in an article on set theory and anyhow the theorem I included was proving the uncountability of the reals (shouldn't a reader be able to read as many proofs of this fact on Wikipedia as he wants?) (Wikipedia is an encyclopedia, yes, but you can't be so restrictive as to not include anything apart from what the article's subject is) (I certainly find any proof of the uncountability of the reals interesting).
But since the issue is not sorted out there is no need to discuss it again.
Topology Expert (talk) 08:02, 5 December 2008 (UTC)
Stallings has recently passed away and this news is now spreading through the math community (see for example [7]) I put a current event tag on the article. Others may wish to watchlist the article for a time. --C S (talk) 21:46, 1 December 2008 (UTC)
- I've changed from the "current event" template to the more specific "recent death" template. And likewise for Beno Eckmann, who died on Tuesday, November 25th. Once the precise date of death is known, Stallings should be added to the list at Deaths in November 2008. Michael Hardy (talk) 03:03, 2 December 2008 (UTC)
- If someone has a WP:V reference re Stallings' death, please add it to the article. There is still nothing at the Berkeley math department website although I see that they have removed his name from the faculty list. I got a couple of private e-mails about his death but nothing passing WP:V. Nsk92 (talk) 14:16, 2 December 2008 (UTC)
- The Berkeley math department posted a notice regarding Stallings death at their website[8]. I added a reference to this announcement to the article. Interestingly, instead of discussing his math in detail, they mention a few main facts and refer to the Wikipedia article about him "for more details on his mathematics"... Nsk92 (talk) 00:55, 4 December 2008 (UTC)
User:WWGB insists on removing the recent death tag. Finally, s/he has given a reason: "not recent death". Does this make sense? Stallings has reportedly died on Nov 24. That would not only seem recent but since he is not a Britney Spears type celebrity, we can expect that the articles and information on his death will take longer to come out than a week or two. --C S (talk) 16:37, 5 December 2008 (UTC)
- I asked WWGB about this a couple days ago, to no response. If WWGB removes the tag again without any justification, and again marks it as a minor edit, it would make sense to raise the issue on WP:ANI or some other more public forum. But I don't think there is anything we can achieve by discussing it here. Clearly Stallings' death is "recent" in the naive sense, and {{recent death}} has no specific guidance about how long the tag may remain. The best outcome would be for WWGB to explain his or her concerns with the tag. — Carl (CBM · talk) 16:58, 5 December 2008 (UTC)
- P.S. It should also go without saying that, if the tag is removed again, a discussion on the talk page about it would be warranted instead of immediate re-insertion. — Carl (CBM · talk) 17:02, 5 December 2008 (UTC)
OK, I've finally added Stallings to the list of deaths in November 2008. I didn't do this earlier because I didn't know the precise date of death. In included a link to the Berkeley page announcing his death, and I notice that the Berkeley page includes a link to his Wikipedia article. Michael Hardy (talk) 17:38, 5 December 2008 (UTC)
I like math, but new to wikipedia math[edit]
I have been working over on WP:DERM for a while, but am looking to work on the Gabriel's_Horn article, as I also have an interest in math. However, I am not as familiar with the WP mathematics policies, and wanted to know if someone could point me in the right direction. For example, I would like to expand the derivation of Gabriel's_Horn so that there are "smaller" steps. Would this be ok to do. Also, I do not notice any sources on that page. May I cite a mathemathics book within the dervation, or does math speak for itself? Thank you all for your help in advance! kilbad (talk) 17:09, 2 December 2008 (UTC)
- I'm quite new and not an expert either, but here's my advice. Have a read of WikiProject Mathematics. About the proof, I think it would definitely be a good idea to expand any parts which are not clear. There is some discussion about proofs at WikiProject Mathematics/Proofs in case you want to wade through that. And yes, of course, all articles should be referenced. And welcome! Martin 17:23, 2 December 2008 (UTC)
- I just had a look at that article, I'm no expert either but I think it looks like a good one to get a feel for what wiki is in aid of. There seems to be a lot of people wanting to write maths equations but few wanting to make it readable or to provide citations. In fact ther seems to be a constant battle against people who want to remove any explanations and just turn it inst a sequence of equations. So yes citation and simplifying is a very good idea. Dmcq (talk) 19:16, 2 December 2008 (UTC)
- The Manual of Style for Mathematics is perhaps the most useful reference for writing mathematics articles. A lot of discussions on proofs and citations are out of date. Times have changed. Geometry guy 19:21, 2 December 2008 (UTC)
- Every article should contain at least one citation. zeteo.info is a database I wrote; it contains a lot of math & physics references (about 11.000). In case you know what book you want to cite, it is usually a matter of seconds to look it up there and add it to the article. Jakob.scholbach (talk) 09:46, 3 December 2008 (UTC)
- Thanks that looks good. I think all citations should use templates like that database does. That makes it easier for robots and suchlike to pick out citations and do useful things with them. Dmcq (talk) 10:49, 3 December 2008 (UTC)
- Depends on the citation. Mathematical citations tend to have fewer examples of the sort of complication that can make citations in the humanities not fit the templates well; but Euclid should be cited by book and proposition, not page number (in one of the hundreds of editions). Septentrionalis PMAnderson 17:03, 6 December 2008 (UTC)
- Thanks that looks good. I think all citations should use templates like that database does. That makes it easier for robots and suchlike to pick out citations and do useful things with them. Dmcq (talk) 10:49, 3 December 2008 (UTC)
- Every article should contain at least one citation. zeteo.info is a database I wrote; it contains a lot of math & physics references (about 11.000). In case you know what book you want to cite, it is usually a matter of seconds to look it up there and add it to the article. Jakob.scholbach (talk) 09:46, 3 December 2008 (UTC)
- The Manual of Style for Mathematics is perhaps the most useful reference for writing mathematics articles. A lot of discussions on proofs and citations are out of date. Times have changed. Geometry guy 19:21, 2 December 2008 (UTC)
- I just had a look at that article, I'm no expert either but I think it looks like a good one to get a feel for what wiki is in aid of. There seems to be a lot of people wanting to write maths equations but few wanting to make it readable or to provide citations. In fact ther seems to be a constant battle against people who want to remove any explanations and just turn it inst a sequence of equations. So yes citation and simplifying is a very good idea. Dmcq (talk) 19:16, 2 December 2008 (UTC)
Mayer–Vietoris sequence[edit]
Any criticism about the Mayer–Vietoris sequence article would be appreciated.GeometryGirl (talk) 17:47, 5 December 2008 (UTC)
- In addition to this Good Article nominations, there are two other: Robert Hues and vector space. Please do consider giving one of the three a review. Thanks Jakob.scholbach (talk) 20:03, 5 December 2008 (UTC)
And on that note there are a few suggestions at Talk:Vector space as to how the article can be improved. Improvements are welcome.
Topology Expert (talk) 17:07, 7 December 2008 (UTC)
Geometric representations[edit]
I know this is a kind of tall order, but i thought if i mention it, some people would possibly keep this in mind. There are some people, such as me, who don't really understand Algebra, but have an intuitive understanding of geometry. This means that if you explain something to me using algebraic notation, i won't understand a thing, but if you plot it on a piece of paper, I will most likely get it. I know I'm not the only one like that. Would it be possible, in the creation of new articles and the overhaul of older ones, to try to - in addition to the legions of formulas - give a geometric representation as well? Thank you very much for your time and effort, and for making wikipedia a more comprehensive resource - hopefully for everybody.-- ExpImptalkcon 00:27, 3 December 2008 (UTC)
- Surely you are not the only like that! Here is a bold proponent: [9] On the other hand, curiously, a student told me once: "I understand everything you say, but nothing you draw!" Also I remember, Wendelin Werner told me once that some of his students complain: "You do not prove, you only draw pictures!" Boris Tsirelson (talk) 07:26, 3 December 2008 (UTC)
- Absolutely. If an image makes it clearer, then adding one is a good thing. Jakob.scholbach (talk) 09:43, 3 December 2008 (UTC)
- You might be interested in the VARK model in Learning_styles#Other_models. I'd put in as many different modes as possible that are relevant. Text, equations, pictures, some articles produce sounds, it is a pity we can't produce feelies yet and somehow it seems unencyclopaediac to ask people to move around. Dmcq (talk) 11:04, 3 December 2008 (UTC)
Having an intuitie understanding of geometry is very important to be able to do it (to do any math subject, you have to understand it intuitively; you can't just expect to write down the correct result from the top of your head). An image can help to illustrate a concept but an image is never a replacement for the formal definition.
Topology Expert (talk) 18:06, 4 December 2008 (UTC)
- Not if you make a formal grammar for the pictures you use, and make a pictorial language that is as precise as a written language. The standard representation of knots is an example. Probably the original diagrams in Euclid's elements were like that. Feynman diagrams for field theory and Penrose diagrams for tensor manipulations are formal pictorial languages, and David Harel's Higraphs are too.
- Mathematicians do not like formal definitions which are in formal languages not obviously derived from the symbols used in standard formalizations of set theory. The reason is that it takes some training to pick up grammars efficiently, and unlike a generation of computer programmers, most mathematicians have not had this training.Likebox (talk) 18:53, 4 December 2008 (UTC)
- Making incorrect blanket statements about mathematicians aside, Topology Expert is simply trying to make sure that formal definitions aren't replaced with "intuitive" drawings. Anyways, though an image is not a formal definition, a picture that is part of a formal language is a formal definition. Of course, one has to formally define the formal language... RobHar (talk) 22:22, 4 December 2008 (UTC)
- Yes, I agree. But I notice that in mathematics texts, a definition in pictures which is perfectly ok formally is sometimes rejected as less rigorous compared to the exact same statement using set-theoretic symbols. That's not a preference for rigor, that's a heavy-handed attempt to standardize everyone on set-theoretic language. Perhaps the best thing to say is that the pictures one uses, like the diagrams in Euclid, should always have an interpretation as precise expressions in some formal pictorial language.
- The reason I am bringing this up is because forcing people to rewrite expressions as linear text can introduce a serious bias which is not apparent: when you write down symbols one after another in a straight line, certain constructions appear elegant and others appear inelegant. For example, if you use a parenthesized language for tensors, like mathematicians often like to do, the tensor expression R_ijk v^i S^ij contracting R,S and V together would look like R(V,S) or also (S(R))(V) or V(R(S)) or (VxS)(R). The different textual expressions are "naturally isomorphic" expressions for the same thing. Using the index notation makes it manifest that they are the same thing. But index notation is considered "ugly" as text, because it doesn't parenthesize in a natural way. In a graphical notation, index expressions look much simpler, and the bias towards easily parenthesized expressions is removed. This is also the reason that Feynman diagrams are much better than algebraic expressions to describe quantum fields--- the different index contractions have a natural representation as graphs and the symmetries of the graph are not preserved if you write them as an algebraic expression in a line of text.Likebox (talk) 23:04, 4 December 2008 (UTC)
- The dislike of index notation among mathematicians has very little to do with aesthetics and more with the fact that using indices implies a choice of coordinates, and thus obscures independence from the choice of coordinates. (TimothyRias (talk) 16:22, 9 December 2008 (UTC))
- Well, there are abstract indices, which are coordinate-independent. Not that I advocate using these necessarily. siℓℓy rabbit (talk) 16:26, 9 December 2008 (UTC)
The following points apply:
a) The _ looks ugly, yes. Therefore, we have LaTeX.
b) Commutative diagrams are images and I would accept that as a formal definition. But my point is that you cannot replace a formal definition with an image; not that you cannot add an image as an accompaniment to a formal definition.
Topology Expert (talk) 08:07, 5 December 2008 (UTC)
- My only point is that a formal definition is also a drawing on a page: it is a bunch of squiggles that look like "A Floo" followed by a squaggle "=" then a doodle "{ a in S | S = Union_i Q_i }". These doodles are no more precise than a diagram with a formal interpretation, so you can often replace a formal textual definition with a formal image defintion. Commutative diagrams are an example, but not the best example, because their semantics is not very complex.Likebox (talk) 15:53, 5 December 2008 (UTC)

Sometimes even when the semantics are ad hoc and informal, an image can be a much easier and still perfectly rigorous way of describing a mathematical object. Example: there exist 20 points in a 10x10 grid such that no three of the points are collinear. One can easily give a picture (right), which should be completely convincing. But describing those points in text (e.g. by giving their coordinates) would be tedious and error-prone. In fact, if I were given a list of 20 text coordinates and asked to verify whether they had this property, I think the easiest way to do so would be to draw the picture; I'd much rather do that than hand-enumerate all 2280 triples of points and go through a 3x3 determinant calculation for each triple to verify symbolically that they are non-collinear. —David Eppstein (talk) 16:19, 5 December 2008 (UTC)
Yes proofs can use pictures (like many category theoretical arguments (I would classify a commutative diagram as a picture) or even the proof of the homotopy lifting lemma). In fact, I think that most people would prefer to prove simple facts like that the nth homotopy group of a space is actually a group by using pictures rather than giving a complex formulae for homotopies. Topology Expert (talk) 15:52, 9 December 2008 (UTC)
- Agree with David's example but in general you should aim for the formal definition.
Topology Expert (talk) 20:42, 7 December 2008 (UTC)
You don't get it do you (for a start, the image constitutes a proof; not a formal definition)? Topology Expert (talk) 15:52, 9 December 2008 (UTC)
- You seem to completely not getting it. The picture is not a proof. A proof needs to confirm that the points in the configuration indeed are never collinear. In this case it is an easy proof by inspection, but that would be quite a challenge if I were to present you a configuration on a 1000x1000 grid. The picture however does give a formal definition of the configuration of which the claim is that no triple of points is collinear. This is a very good example of where it is much easier to give a formal definition of a mathematical object (in this case a configuration on a grid) by using picture rather set theoretic language. Of course, to really be a formal definition one first needs to rigorously define what such a picture means. (TimothyRias (talk) 16:15, 9 December 2008 (UTC))
- No I get it. The picture is a proof but not a formal proof. Topology Expert (talk) 20:50, 9 December 2008 (UTC)
- That reminds me of a joke I once heard. But first, I need to give a few definitions... siℓℓy rabbit (talk) 16:18, 9 December 2008 (UTC)
- On another line of thought: So this picture is an example of a special case where it is easier to define something formally using a picture than using set theory. Is there an example for the converse? Does somebody have an example where a non-set-theoretic object is most clearly defined in the language of set theory, and not in some other way?
- I tried to think of examples: the first examples I thought of were all in point-set topology. But this is not very good, because point set topology itself was a heavy handed attempt to shoehorn topology into the language of set theory. In fact, because of the language change, the questions and concerns of point-set topology drifted off so much from the realm of what used to be called topology or "geometria situs" and is now called algebraic topology that the two fields are now completely distinct. Point set topology gets less attention everywhere except the undergraduate curriculum, and the theorems of the field are notoriously subject to undecidability issues stemming from their over-broad categories that rely on the ordinal structure of the set theory. Almost all the examples that I came across for for theorems of dubious validity, those that can be forced one way or another by changing models of set theory, come from point-set topology.
- The other example is for ring ideals, the usual definition is as subsets. I feel that this example is also unsatisfactory, since the theory of ideal divisors was developed by Kummer and Kronecker using a formal language divorced from sets, and was later retroactively refitted for set theory, just like topology. Hermann Weyl's book on algebraic numbers describes the earlier mostly equivalent approach, and I think it is clearer than the standard approach.
- Another example is logic, and model theory. But the primitive manipulations of set theory are almost identical to the primitive operations of logic, except reinterpreted to apply to objects in a model rather than to propositions. Union is "or", intersection is "and", set complement is "not", etc, etc. So really, the language of set theory is just a model-theoretic reformulation of proof analysis--- it reinterprets propositions as objects, the sets which satisfy those propositions, and reinterprets fundamental logical operations of logic as operations on objects. There's nothing wrong with that of course, but it's a bit "low-level". I think that nearly all fields of mathematics would like to operate with formal languages at a higher level of sophistication, more divorced from the machinery of logic. So while proof theory is a good example of something that is clarified by set-theoretic language, it also is not a good example, because set theory and proof theory are nearly synonyms.
- So are there any good examples? One more comes to mind--- the notion of amenability in groups. This is a set-theoretic notion in measure theory applied to groups, and people talk about it a lot. But I think that there really ought to be a way to state this notion more clearly, so that it does not rely on set-theoretic notions. I have no idea how to do that. So ok, there's one tentative example. Are there other examples?
- Elementary topoi come to mind here. I don't think they necessarily provide the examples that you're looking for, but they do show that some areas of math can be done in a completely rigorous and formal way without sets. E.g., standard differential geometry can be replaced by synthetic differential geometry. Ozob (talk) 01:03, 10 December 2008 (UTC)
"Boubaker polynomials", again[edit]
Hello experts, some time last year there was some hullabaloo about repeated recreation, apparently by COI socks, of an article about so-called Boubaker polynomials. The consensus turned out to be there were no reliable independent sources establishing notability, and I closed the latest Afd (Wikipedia:Articles for deletion/Boubaker polynomials (2nd nomination)) as "delete with prejudice against re-creation". Now, there is again a new editor, Luoguozhang (talk · contribs), who has recreated Boubaker polynomials and a second, related article at BPES (guess what the "BP" stands for).
It does seem to me that he is now citing some independent sources, but I have no idea about the topic area and can't judge reliability. Can people with more topic knowledge please go and check if those articles are legit? Fut.Perf. ☼ 18:42, 6 December 2008 (UTC)
- The references do need a bit of scrutiny. Note how the are all given as a single person et al, with the person chosen to be not Boubaker. Looking at the first ref it turns out to be: Boubaker, K.; Chaouachi, A.; Amlouk, M.; Bouzouita, H. (2007). I'm fairly sure most of the other refs will turn out to have Boubaker as a co-author. --Salix (talk): 20:46, 6 December 2008 (UTC)
- Well, one can certainly check this. Among the references to published papers, the ones which do not include Boubaker as a coauthor are [2] = [18] (i.e., the same paper appears twice in the list), [13] and [19].
- I do find it curious that Boubaker is listed out of alphabetical order as a second author on the majority of papers in which his name appears in the title (in theoretical mathematics, putting authors' names out of alphabetical order at all is rare enough for eyebrows to be raised, so I have no idea what meaning is supposed to be conveyed by a non-alphabetical order). I think it is unacceptable for an entry in a formal reference list to read [First author, et al.], for almost the opposite reason: that is completely disrespectful to the other authors of the paper.
- Overall this article is a bit over-referenced, e.g. the citation of Boubaker polynomials at tripatlas.com is quite silly. But I have to say that, as a complete outsider to these particular deletion discussions, I don't see what all the fuss is about. We have an article about a concept which has been discussed prominently in multiple peer-reviewed journals. Most of the papers are coauthored by Boubaker: so what? One of the necessary conditions for a paper to be accepted in a peer-reviewed journal is for one's peers to be sufficiently interested in the subject matter so as to believe it merits wide dissemination. Anyway, there are three papers on the concept which are not coauthored by Boubaker.
- I agree with your last sentiment, that probably this article should not be deleted. Indeed, many of the references do look reasonable and, for better or worse, they undeniably establish the notability of the subject. However, the broader context of this repeatedly re-created article is that it seems to have inspired more overall abuse of editing privileges (conflicts of interest, sockpuppetry/meatpuppetry, block evasion, and out-of-process article re-creation) than any other mathematics article in recent memory. The article certainly deserves close scrutiny, as do the contributors who created it. siℓℓy rabbit (talk) 21:22, 6 December 2008 (UTC)
- On the other hand I can find no reason for the existence of the article BPES, whose content is contained, verbatim, in Section 1 of Boubaker polynomials. I put a proposed deletion tag on this article. Comments welcome. Plclark (talk) 07:49, 7 December 2008 (UTC)
- Why not just redirect BPES to the Boubaker polynomials article? That's just as simple as proposing deletion and doesn't require anyone else to follow up on it if there is agreement with the redirect. — Carl (CBM · talk) 12:34, 7 December 2008 (UTC)
- Redirection instead of deletion suits me. siℓℓy rabbit (talk) 13:38, 7 December 2008 (UTC)
- Why not just redirect BPES to the Boubaker polynomials article? That's just as simple as proposing deletion and doesn't require anyone else to follow up on it if there is agreement with the redirect. — Carl (CBM · talk) 12:34, 7 December 2008 (UTC)
I've redirected it and deleted the links to it from the main article. Michael Hardy (talk) 14:49, 7 December 2008 (UTC)
- It's now metastasized to Chebyshev polynomials... —David Eppstein (talk) 23:23, 7 December 2008 (UTC)
- Any article that doesn't "metastasize" in that sense needs an "orphan" label asking people to "metastasize" it. Michael Hardy (talk) 17:36, 8 December 2008 (UTC)
- That doesn't look so bad (although I find your analogy ominously apt). I propose that project members should continue to monitor Boubaker polynomials, given its editors' previous abuses. siℓℓy rabbit (talk) 23:32, 7 December 2008 (UTC)
- What previous abuses? Could it be that you meant "given its previous editors' abuses"? Michael Hardy (talk) 17:35, 8 December 2008 (UTC)
- With this sequence of edits (the IP making a change and the account then giving the justification for it in a null edit shortly after), Luoguozhang (talk · contribs) has probably outed himself as another Boubaker sock. It's his known Tunesian IP range. I cannot find any formal decision to ban/indef-block the Boubaker sockmaster earlier, otherwise I would have blocked and deleted right on the spot, but I'll recommend you guys keep that in mind when monitoring the page. Fut.Perf. ☼ 06:54, 9 December 2008 (UTC)
- Mario scolas, a major sockpuppet vandal, was active in editing some old versions of the Boubaker polynomial article, but I doubt he's the same person as Boubaker given scolas' interest in Belgian politics and Boubaker's Tunisian location. Also scolas seems to be the real name of the sockmaster while Boubaker seems to be the real name of someone else. —David Eppstein (talk) 07:34, 9 December 2008 (UTC)
- With this sequence of edits (the IP making a change and the account then giving the justification for it in a null edit shortly after), Luoguozhang (talk · contribs) has probably outed himself as another Boubaker sock. It's his known Tunesian IP range. I cannot find any formal decision to ban/indef-block the Boubaker sockmaster earlier, otherwise I would have blocked and deleted right on the spot, but I'll recommend you guys keep that in mind when monitoring the page. Fut.Perf. ☼ 06:54, 9 December 2008 (UTC)
- What previous abuses? Could it be that you meant "given its previous editors' abuses"? Michael Hardy (talk) 17:35, 8 December 2008 (UTC)
How can someone create so many sockpuppets?
Topology Expert (talk) 15:57, 9 December 2008 (UTC)
Can you help me with citations?[edit]
I started editing the article dependent and independent variables, which was a real mess, and added some cited content under the math section. However, there is all this content under the statistics section that is uncited, and wanted to know if someone would help me find sources for this information, or challenge and remove it? kilbad (talk) 03:12, 9 December 2008 (UTC)
Earliest Known Uses of Some of the Words of Mathematics[edit]
We have dozens of links to the "Earliest Known Uses of Some of the Words of Mathematics" site, but this site has moved and the old links are now broken. The old URLs are of the form http://members.aol.com/jeff570/e.html and the new ones are of the form http://jeff560.tripod.com/e.html . Anyone who feels like updating some of these links can find them using the LinkSearch page. --Zundark (talk) 09:34, 9 December 2008 (UTC)
- You might want to ask at WP:BOTREQ. —Ilmari Karonen (talk) 20:37, 10 December 2008 (UTC)
If anyone has some time, could they have a look at the Branch point article? It only gives an informal description before listing some examples, and finally mentions its usefulness and development in Riemann surface theory in the last couple of sentences, but again doesn't really give anything very concretely. I had a look at a few complex analysis books I had handy, and, well they tended to keep it pretty informal too, so I don't feel too confident having a crack at this myself. Cheers, Ben (talk) 12:12, 10 December 2008 (UTC)
The concept is pretty basic in complex analysis (and in algebraic geometry) so I think you should have a go at editing it. After all, you should have a go. If at all you make a mistake, someone can easily correct it. I will add some examples to that page (and a proper formal definition for a start) and note that the branch point is defined only for holomorphic functions. Basically, a branch point of a holomorpic function (defined of course on the complex plane), is simply a point which gets mapped onto different values depending on its complex argument. Basically, a point z in the complex plane has countably many arguments (if its argument is θ, then its argument is also θ+2πn for all n in Z) and if the function value of z depends on the argument you choose, then z is called a branch point. The most obvious example of a function whose every point is a branch point is the function mapping a complex number to its argument. An example of a function with no branch point is the function mapping a point to its modulus. Think about this and have a go at editing the article. If I get time I will add a few facts myself.
Topology Expert (talk) 13:46, 10 December 2008 (UTC)
- Ummm ... but surely arg(z) and |z| are not holomorphic functions ? Gandalf61 (talk) 13:58, 10 December 2008 (UTC)
Nope, they aren't. But I don't see why 'holomorphic' has to be included in the definition (as long as the functions are continuous and you can 'speak of' the change of a function along any path in the complex plane, that should be enough. And surely f is differentiable on any path in the complex plane?).
Topology Expert (talk) 14:18, 10 December 2008 (UTC)
I added an equivalent (from the top of my head) definition to the article on branch point of a branch point of a function using the notion of a winding number. Anyone care to have a look at it (the second definition)? In my opinion the one I added from the top of my head is probably more mathematically formal.
Topology Expert (talk) 14:20, 10 December 2008 (UTC)
The article (in the section on Riemann surfaces) writes the following:
The concept of a branch point is defined for a holomorphic function ƒ:X → Y from a compact Riemann surface X to a compact Riemann surface Y (usually the Riemann sphere). The function ƒ, unless it is constant, will be a covering map almost everywhere
This is meaningless in the sense that what does 'almost everywhere' mean. It can't be in the context of measure theory because there is no natural way (i.e to make a Riemann surface into a measure space such that the two structures are compatible) to make a Riemann surface into a measure space (forgive me if there is; I am not an expert on the subject). So what does it mean? Perhaps it (most likely) means that the map f is a covering map for all but a finite number of points but if so, this should be explicitly mentioned (and made more precise). Any opinions?
Topology Expert (talk) 14:43, 10 December 2008 (UTC)
It also depends on what you consider a ‘covering map’ (i.e, whether you require a covering map to be surjective or not). But since the ‘result’ specifically excludes the constant map, it is probably not surjectivity (the constant map will yield a non-discrete fibre and hence cannot be a covering map).
Topology Expert (talk) 14:55, 10 December 2008 (UTC)
- This totally needs to be on the talk page by now. Ryan Reich (talk) 15:11, 10 December 2008 (UTC)
I will copy this section there but let us continue it here because there are currently disputes regarding the material in that article (and hence we want as many mathematicians as possible to give their opinions). No one is going to go to the talk page of that article within a 100 years anyhow!
Topology Expert
- I echo Ryan: "This totally needs to be on the talk page by now." Discussions about a specific article should go on the talk page of that article, otherwise this page becomes unwieldy. This page can be used for discussions that concern a lot of articles, or to point at discussions at other places if you expect that people from this WikiProject are interested in it. -- Jitse Niesen (talk) 16:04, 10 December 2008 (UTC)
- (ec w/Jitse) Now that anyone who reads this page knows where the discussion is, they will. It seems to be customary, even with disputes that as many mathematicians as possible should know about, to leave a one-liner here with a link to the relevant forum. Which is where I'll be going. Ryan Reich (talk) 16:08, 10 December 2008 (UTC)
OK
Topology Expert (talk) 17:17, 10 December 2008 (UTC)
LaTeX is broken bug[edit]
Is anyone else getting errors like this
- Failed to parse (Cannot write to or create math output directory)
on perfectly good LaTeX code every now and again? Is this something that the devs should be bothered with? siℓℓy rabbit (talk) 22:24, 7 December 2008 (UTC)
- This happened to me earlier in the article Selberg trace formula. I edited the talk page (added the math rating template), and then when I went back to the article, the formulas looked like that (though they didn't before). I fixed it by doing a null edit on the page. But it is a weird bug that the developers might want know about (not that I really know what they want to know about). RobHar (talk) 22:38, 7 December 2008 (UTC)
- It seems to be a sort of heisenbug. If I reload the article, then it vanishes. In my case, the browser I use by default dumps the local cache when I reload, so I'd bet that the null edit forced your browser to do the same thing. (In other words, the null edit probably didn't have any server-side effect, but I could be wrong.) siℓℓy rabbit (talk) 22:45, 7 December 2008 (UTC)
- Well I tried, forcing the reload on my computer, and when that didn't work, I went over to my other computer and the page was still not displaying well. I went to the history of the page and clicked on the most recent version and it displayed well, so I "edited" it. I dunno. RobHar (talk) 22:48, 7 December 2008 (UTC)
The same thing just happened to me. Paul August ☎ 03:55, 9 December 2008 (UTC)
- One of the 200 or so Wikimedia web servers had the filesystem containing the LaTeX image directory unmounted. Since requests are distributed among the servers essentially at random, any time you loaded a page with <math> tags on it you'd have about a 0.5% chance of getting the error. I eventually managed to figure out which server was the broken one, and reported it to Tim Starling, who fixed it. Shouldn't happen any more. —Ilmari Karonen (talk) 20:54, 10 December 2008 (UTC)
- Nice detective work. Paul August ☎ 08:43, 11 December 2008 (UTC)
"Completeness relation" in "Hermite polynomials"[edit]
The "completeness relation" section in Hermite polynomials is not clearly written. Obviously whoever put it there was verbally challenged. I can't tell what it says. Not that I've exerted great effort on the point, but the meaning should be clear without that. Can someone help? Michael Hardy (talk) 18:08, 11 December 2008 (UTC)
I may not have exactly got what is necessary (someone will have to fix up the LaTeX) but I basically only cleaned up the verbal bit (perhaps 'logically challenged' would be less insulting and more appropriate). Topology Expert (talk) 20:27, 11 December 2008 (UTC)
Silly rabbit fixed up the LaTeX. How does it look now?
Topology Expert (talk) 20:42, 11 December 2008 (UTC)
Question[edit]
Please can any one tell me if these polynomials have any Exponential Generating Function and if their roots have any analytical expression ? (and please where can one find the Exponential Generating Function for Chebyshev Polynomials ?? Duvvuri.kapur (talk) 22:32, 12 December 2008 (UTC)
Some external links[edit]
New user Wayp123 has been adding a number of links to his/her website [10] and, after my deleting them, wishes to reinsert them. I don't see the notability of the site, but wanted to post here to discuss this in more generality (affected articles include matrix (mathematics) and linear map). Jakob.scholbach (talk) 06:27, 8 December 2008 (UTC)
- I see no value in these links. Paul August ☎ 06:58, 8 December 2008 (UTC)
- There is only value in them, like any other link, if the user decides to click and follow up on them. The only thing that has no value is the un-thought-of Wayp123 (talk) 09:55, 8 December 2008 (UTC)
- Try the Open Directory Project. This is an encyclopedia, not a web directory. But I am not even sure that the ODP would accept your site. --Hans Adler (talk) 16:01, 8 December 2008 (UTC)
- The point of an encyclopaedia is to spread knowledge, If everyone knew everything, like they are supposed to with my link, then why have an encyclopaedia. Wayp123 (talk) 16:43, 8 December 2008 (UTC)
- Because there is too much information out there for anyone to know all of it. An encyclopedia needs to give the pertinent information on a subject. If wikipedia included links to every single helpful website out there, then there'd be too much information in the external links section. RobHar (talk) 16:59, 8 December 2008 (UTC)
- How many other websites have some of the wiki articles in a talking picture book format. Wayp123 (talk) 17:05, 8 December 2008 (UTC)
- How many other encyclopedias contain links to cryptic websites that only contain downloadable content that can't be used without an obscure shareware ($ 10) programme that only runs under Microsoft Windows. Please note that Wikipedia is a relatively hostile environment for the more straightforward types of guerrilla marketing. --Hans Adler (talk) 17:20, 8 December 2008 (UTC)
- How many free(needs donations) online encyclopaedias are there? Not all websites are the same, some do and some don't have downloadable content. Since it is shareware, the $10 is optional. Yes for now only on Windows, later on others, once my donations catch up with the work. Wayp123 (talk) 17:38, 8 December 2008 (UTC)
"New" user Wayp123 is in a strict sense not "new", since he was previously warned for spamming more than 2 years ago. But perhaps "new" in the sense of only having made intermittent spamming forays into Wikipedia and not really understanding how it functions. --C S (talk) 04:24, 9 December 2008 (UTC)
- If I only put in one link will that be considered spamming, or if I donate per link will that be better. Wayp123 (talk) 08:48, 9 December 2008 (UTC)
- You should read Wikipedia:External links which explains some of the principals behind what links are preferred. The inclusion of links is purely an editorial decision so cannot be purchased. In general links which don't need external programs are prefered and they should include content not found in the article rather than a representation of the material. --Salix (talk): 09:03, 9 December 2008 (UTC)
- Yes they are just guidelines, to help prevent complaints, subject to editorial decision. Yes it is a copy of the material, but I think it is presented in such a way as to help those who find reading difficult, so it adds value to the material. Has anyone else tried the material before passing judgement? Wayp123 (talk) 09:15, 9 December 2008 (UTC)
- Personally I consider it a failing of wikipedia if it isn't suitable for reading by any standard tool users use for web pages. It doesn't sound to me like the links lead to extra information about the subjects so they don't qualify on that ground. Perhaps what you want is to provide some javascript people could add to their preferences to make linking to your site easier. I think that might be acceptable. Dmcq (talk) 09:46, 9 December 2008 (UTC)
- Yes it is something I would like to do, but for now, if the site is too difficult to use then they can just leave again, although people interested in math should not find anything difficult. There is nothing wrong with Wiki, my material is just different, it makes for a more pleasant reading experience. Wayp123 (talk) 10:03, 9 December 2008 (UTC)
- Can I make the link look like this: Talking Picture Book version - of this article. The site requires that you download a windows module before you can use the material.Wayp123 (talk) 11:27, 9 December 2008 (UTC)
- I think everyone except you deems it not complying with existing rules/guidelines, so I'd ask you not to put the links. Jakob.scholbach (talk) 11:58, 9 December 2008 (UTC)
- I see there is a link on the Matrices page that only uses windows software. Wayp123 (talk) 12:39, 9 December 2008 (UTC)
- Most of those links should be deleted. I have tagged the page with a {{cleanup-links}} template. siℓℓy rabbit (talk) 12:50, 9 December 2008 (UTC)
- I think its stupid to delete perfecly good links. So what if they only windows, they add value a web page cant do. Wayp123 (talk) 13:02, 9 December 2008 (UTC)
- Wayp, you seem to be the only one who thinks these links are appropriate. I suggest you drop this and help remove them from the articles. Martin 13:05, 9 December 2008 (UTC)
- To be safe and politically correct, lets remove all external links. I wont talk if you dont. Wayp123 (talk) 13:08, 9 December 2008 (UTC)
- See WP:POINT. siℓℓy rabbit (talk) 13:22, 9 December 2008 (UTC)
(ec) The principle behind Wikipedia, and the reason for its success, is WP:CONSENSUS. While consensus cannot usually be measured in terms of head counting, it seems quite easy in the case of this discussion. For inclusion: Wayp123 (1 editor, note WP:COI). Against inclusion: Jakob.scholbach, Paul August, RobHar, Hans Adler, C S, Salix alba, Silly rabbit, Msgj (8 editors). Please stop beating this dead horse. --Hans Adler (talk) 13:28, 9 December 2008 (UTC)
I think you are all paid wiki staff so I have no say. Wayp123 (talk) 13:39, 9 December 2008 (UTC)
- I wish! Martin 13:44, 9 December 2008 (UTC)
- Exactly who would get money out of this? I'm constantly amazed the way people say of others what's true of themselves. No I don't contribute for fame or fortune or even for the society, sorry folks ;-) Dmcq (talk) 16:57, 9 December 2008 (UTC)
Neither do I. I just like to contribute for fun. Topology Expert (talk) 17:05, 9 December 2008 (UTC)
Goodbye for now, Ill be back! Wayp123 (talk) 13:50, 9 December 2008 (UTC)
That's an interesting point: On the survey, there was a question asking whether you are paid for editing Wikipedia (i.e Question: What is your reason for editing Wikipedia? and Choice: Because I am paid to do it). Maybe people are paid...
Topology Expert (talk) 14:08, 9 December 2008 (UTC)
By the way, aren't C S and silly rabbit supposed to be on a wikibreak? (I couldn't resist myself either! I wonder whether anyone who put a wikibreak tag on his page has actually managed to pull it off...).
Topology Expert (talk) 14:12, 9 December 2008 (UTC)
Oh, I nearly forgot: My daughter lost her gloves at the staff Christmas party last night. If one of you found it, could you please put it on my desk tomorrow? Thanks. --Hans Adler (talk) 17:50, 9 December 2008 (UTC)
Have you gone mad? (or is it just that I don't get the joke here?)
Topology Expert (talk) 17:59, 9 December 2008 (UTC)
- The idea raised by Wayp123 that we are all paid Wikipedia staff is laughable. Instead, once a year, Wikipedia asks us to give money to the foundation, not vice versa! You can add my view to the obvious consensus that the links are inappropriate. Move along please, nothing to see here. Geometry guy 20:31, 9 December 2008 (UTC)
Lol! G g, didn't you know that the rest of us are secretly employed by the WP:CABAL? siℓℓy rabbit (talk) 20:39, 9 December 2008 (UTC)... I mean, there is no cabal... siℓℓy rabbit (talk) 20:39, 9 December 2008 (UTC)- Narrow escape there S r! As I'm sure you know, not only is there no cabal, but anyone who says there is will be banned, tried in absentio, taken to a quarry and executed with a knife. :-) Geometry guy 22:04, 9 December 2008 (UTC)
Current score: 9 paid Wikipedia staff members — 1 independent contributor who is only interested in improving the encyclopedia. --Hans Adler (talk) 21:44, 9 December 2008 (UTC)
- Lol. Did no one tell TopExp about the Christmas party? Martin 22:26, 9 December 2008 (UTC)
- He missed a lot. Paul August's fancy dress was not very seasonal, but the ladies seemed to like it anyway :-) Geometry guy 23:47, 9 December 2008 (UTC)
- Yes well the ladies always like my fancy dress, the drab one, not so much. Paul August ☎ 08:46, 11 December 2008 (UTC)
- The part where Charles Matthews danced naked on the table after having more than the usual amount to drink didn't really appeal to my tastes. Michael Hardy (talk) 23:53, 9 December 2008 (UTC)
- He missed a lot. Paul August's fancy dress was not very seasonal, but the ladies seemed to like it anyway :-) Geometry guy 23:47, 9 December 2008 (UTC)
To tell you the truth, I'd rather not hear about this party anyway. Topology Expert (talk) 11:00, 10 December 2008 (UTC) How do you know that I was not there? Topology Expert (talk) 20:05, 10 December 2008 (UTC)
- I went dressed as the 1960s (remember them well ...) - it was somewhere else, man. Charles Matthews (talk) 21:36, 11 December 2008 (UTC)
I noticed that the day after the party, a team of plumbers were called to the venue. I am still baffled about this but I think it had something to do with the fact that David Eppstein was in the toilets for more than an hour. Topology Expert (talk) 22:43, 12 December 2008 (UTC)
Mathematics Question[edit]
Please can any one tell me if the Boubaker polynomials have any Exponential Generating Function and if their roots have any analytical expression ? (and please where can one find the Exponential Generating Function for Chebyshev Polynomials ?? Duvvuri.kapur (talk) 22:34, 12 December 2008 (UTC)
Please ask this at the reference desk. Topology Expert (talk) 22:44, 12 December 2008 (UTC)
Thanks, we did not know the existence of this page..
Duvvuri.kapur (talk) 23:39, 12 December 2008 (UTC)
Group actions and Orbit space[edit]
The article on group actions contains a bit about orbit spaces (namely when a topological group acts on a topological space, one can consider the collection of all orbits as a quotient space) but such an important concept (namely the theory of Lie groups/topological groups acting on topological spaces) deserves its own article (I can explain its importance in mathematics if necessary). One very important application is:
- Principal G Bundles (which are used to calculate homotopy groups)
I can create the article but I would appreciate it if some people could help out there (I am sure there are many applications which I would not know about).
Topology Expert (talk) 15:08, 10 December 2008 (UTC)
Also there should be a proper article on orbit space. What would we call the article (namely the article describing the theory of topological groups/Lie groups acting on topological spaces) if we were to create it?
Topology Expert (talk) 15:09, 10 December 2008 (UTC)
- See also Orbifold. But orbifolds aren't quite the same thing as quotients of manifolds, they are things that look locally like quotients. —David Eppstein (talk) 08:26, 11 December 2008 (UTC)
Yes, I forgot about orbifolds! But they really don't completely discuss the whole theory behind topological groups acting on topological spaces. Topology Expert (talk) 09:15, 11 December 2008 (UTC)
Isn't anyone else going to comment on whether this idea is good or not? Or at least list some other concepts in this theory that they know? I think that there should be a category on this (just like there is a category:topology). Opinions (I am disppointed at the lack of enthusiasm when a subject related to topology is bought up. I know that there are lots of knowledgeable people on the subject (here) but most don't seem interested enough to comment. I once raised awareness that the article on fibre bundles is under par along with some (in fact a lot of) comments but no-one bothered to do anything until I personally asked some editors on their talk page)? Topology Expert (talk) 14:17, 13 December 2008 (UTC)
TeX square plus[edit]
You can get symbols inside a circle with oplus,ominus,otimes but how do you get symbols inside a square ? This is needed for the article gyrovector space. Delaszk (talk) 16:27, 13 December 2008 (UTC)
hostile edits at Bishop–Keisler controversy[edit]
A pair of editors have explicitly stated that they are in favor of deleting the article. It is of course their right to nominate the page for deletion. In the meantime, they are involved in edits that tend to degrade the quality of the article, in some cases based on ignorance of NSA. Can a case be made that if their intention is to delete it, they should refrain from further damaging edits so as not to predetermine the outcome of a deletion discussion? Katzmik (talk) 08:18, 11 December 2008 (UTC)
- Now that I understand that you own the article, I have reverted the article back to your edit, in which you removed my "essay" tag and all of Thenub314's edits. Mathsci (talk) 09:05, 11 December 2008 (UTC)
- I suggested over a week ago that we discuss the contents of the article on the talk page. I did not get any feedback from either of the editors involved. Therefore I made certain changes that in my opinion improved the article. I suggest we continue this discussion on the talk page in question and refrain from wholesale deletions unless these have been previously discussed. Katzmik (talk) 15:41, 11 December 2008 (UTC)
- I see there is a recommendation for a deletion on the article page, but I don't see any link to a deletion discussion page. What is the current status of the article exactly? Katzmik (talk) 15:46, 11 December 2008 (UTC)
- Read the deletion notice, and WP:Proposed deletion which it links to. Algebraist 15:47, 11 December 2008 (UTC)
- I see there is a recommendation for a deletion on the article page, but I don't see any link to a deletion discussion page. What is the current status of the article exactly? Katzmik (talk) 15:46, 11 December 2008 (UTC)
- What happened to an assumption of good faith? I was very surprised to check to see what was happening at the project page and see a discussion about myself, for I am responsible for most of the edits being discussed. I feel like I should describe the situation. I was away from Wikipedia for a while and sadly did not notice Katzmik's request to discuss the article on the talk page. Upon returning I noticed some things in the article that I thought should changed and changed them. I feel my edits were not hostile, but intended to improve the article. I have for a while been trying to improve the article, adding references, etc. and after carefully thinking the matter over I felt this subject didn't deserve to have an article of its own. I had requested on the talk page that someone explain why the article was about more then a scathing book review, and felt this question was never answered. So, I suggested on the discussion page that the article should be deleted. Another editor agreed, so I proded the article (which may be inappropriate, but I am new to nominating an article for deletion, and I am still reading about it.) The prod was taken down and Katzmik requested we wait before taking it up at Afd, which so far we have to my knowlege (and continued the discussion at the talk page).
- If there is a matter of Wikiettique I am missing out on, would someone please point me to where I can read more? I try my best to be a good editor, but there are many ways I could make improvements, and in many ways I am still green to wikipedia. And I understand one should take discussions with a fair amount of ice to keep your temper cool, I can't help but feel a bit upset that it is being suggested that I am making edits specifically to make an article more likely to be deleted. It also would have been nice if this had been brought up on my discussion page, or I were in some way invited to join in this discussion. It is a bit jarring to be reading along and see yourself being referred to as hostile.
- I merged it into nonstandard calculus. The old article can be redirected, if everyone agrees.Likebox (talk) 20:39, 12 December 2008 (UTC)
I initiated a discussion on the talk page of the article (and gave reasons as to why I do not support the merge). Topology Expert (talk) 21:50, 12 December 2008 (UTC)
Because I am supposed to follow the 'rules', I have copied the voting into the talk page of the article. Voting there is encouraged. Topology Expert (talk) 22:26, 13 December 2008 (UTC)
- A word of advice. While Wikipedia is not a democracy, neither is it a bureaucracy. The principal method for resolving conflict is consensus. This has proven to be remarkably successful. The "rule" that voting is not a good idea is not a binding constraint, but the product of experience and consensus. If you think a vote will improve the encyclopedia, then by all means continue it on the article talk. However, my experiences of dozens of contentious votes have only confirmed the wisdom of the "rule" (advice) that voting only creates division and seldom leads to progress. Don't be slavish to rules, but heed their wisdom. Geometry guy 22:42, 13 December 2008 (UTC)
(indent) Following the suggestions of numerous editors, the article has now been listed at AfD Wikipedia:Articles for deletion/Bishop–Keisler controversy. Mathsci (talk) 05:28, 14 December 2008 (UTC)
I want to point out that if you merge this article into non-standard analysis, you should at least keep a redirect (not that I support the merge). Since this is a very famous controversy (as several users have pointed out), someone searching it should be able to go to its article and then be redirected. Deletion is simply ridiculous. Topology Expert (talk) 11:09, 14 December 2008 (UTC)
Edit war in Alexander Grothendieck?[edit]
I noticed that there seems to be a passive-agressive struggle in the edit comments of the Grothendieck article over whether he is Category:French people of German descent. Since December 7th, User:Feketekave and a few IP addresses (all similar, so probably the same unregistered editor) have been alternately deleting and re-inserting this category into the article, with Feketekave claiming it is "racialist" and the IP claiming that removing it is "vandalism". There have been now three rounds in this altercation, the two most recent being all four of the latest edits. These two need to be brought to heel and the issue should probably be discussed in the open now as well. I note that Grothendieck's ancestry and nationality have already been the subject of some debate, wherein his being Jewish (or not) was concerned. Ryan Reich (talk) 17:15, 14 December 2008 (UTC)
- More to the point is whether he is stateless, which he has been rumoured to be. Charles Matthews (talk) 18:52, 14 December 2008 (UTC)
- The onus is on the editor adding the category, to support the verifiability. Here there is a genuine problem. Charles Matthews (talk) 21:10, 14 December 2008 (UTC)
Someone has been adding way too much to this category, and at the same time inexplicably missing obvious things like Dehn surgery. I wanted to post here for discussion before I start to unilaterally remove articles from the category. siℓℓy rabbit (talk) 23:20, 5 December 2008 (UTC)
- I agree with you. I'm not too much a connoisseur of surgery theory, but I can't see why homotopy group, for example is put into that category. Jakob.scholbach (talk) 13:18, 6 December 2008 (UTC)
- I have started the long haul. I will use my own judgment on whether something belongs in the category. If I make an error, please correct it. siℓℓy rabbit (talk) 21:52, 6 December 2008 (UTC)
- Well homotopy groups are quite important (if not very important) in surgery theory so they should be there. Topology Expert (talk) 16:48, 7 December 2008 (UTC)
I undid silly rabbit's edit of removing homotopy groups from the Category:Surgery theory because they are used in surgery theory but I don't think they would be called part of surgery theory (an analagous case is the continuum hypothesis which is used in topology but not really part of it). Is this way of adding concepts to a category correct according to the Wiki conventions? I think that homotopy (and homology) groups are very important in surgery theory so because of this importance they should be included in the category but I would like another editor's opinion. Topology Expert (talk) 17:00, 7 December 2008 (UTC)
Well, surgery theory does answer some questions in homotopy (and homology) theory regarding manifolds so I think they should be included. Topology Expert (talk) 17:02, 7 December 2008 (UTC)
- In which of the following categories would you include free group: Category:Group theory, Category:Algebra, Category:Algebraic topology, Category:Homotopy theory, and why? Note that the remarkable theorem that every subgroup of a free group is free is generally proved using covering space techniques, so that homotopy theory is indeed important to the theory of free groups. Category:Topological graph theory is an additional intriguing possibility.
- Also, could you please indent your comments properly? You need to put colons at the beginning of every new paragraph. Ryan Reich (talk) 19:20, 7 December 2008 (UTC)
- Oh yes; that theorem is called the Nielson-Schreier theorem for those who are interested (I will answer your question (unless it is rhetorical) a little later). Topology Expert (talk) 20:26, 7 December 2008 (UTC)
- On that note, I am disappointed that there is so little content on surgery theory in Wikipedia. Maybe that's something I (and other editors who work on the subject) should try to improve. Topology Expert (talk) 17:05, 7 December 2008 (UTC)
- As I suppose Ryan Reich points out, although there is no doubt that homotopy groups, differentiable manifolds, and sundry, play an important role in surgery theory, they certainly aren't conceived as part of surgery theory per se. Remember that the purpose of categories is to aid the reader in navigating related articles. So too many (offtopic) articles in a given category defeats the purpose of categories as much as too few. One needs to be a little selective about the content. siℓℓy rabbit (talk) 20:00, 7 December 2008 (UTC)
- I've added Category:Surgery theory to Category:Homotopy theory. I think that homotopy group should still be removed from the former category, because it more properly belongs in the latter. Any objections? siℓℓy rabbit (talk) 20:08, 7 December 2008 (UTC)
- I agree. —David Eppstein (talk) 20:12, 7 December 2008 (UTC)
- Agree. I was not sure with the Wiki conventions. But I think you will agree that surgery theory has answered problems in homotopy group theory so why shouldn't homotopy groups be included in the category (apart from that I have no objections)? Topology Expert (talk) 20:26, 7 December 2008 (UTC)
- Well, because it crowds the category with off-topic articles. (TimothyRias (talk) 10:52, 8 December 2008 (UTC))
(unindent) OK, here is a question: should homotopy theory be included in Category:Fibre bundle and vice-versa? Any fibre bundle theorist will agree that the 2 are very closely related. Topology Expert (talk) 11:26, 8 December 2008 (UTC)
- You mean Category:Fiber bundles? No, but perhaps fiber bundle ought to be in Category:Homotopy theory, because of the long exact sequence of homotopy groups associated to a fibration. And indeed, it is. I think you are categorizing against the flow of implication, here.
- Clarification: by analogy with what you said about surgery theory and homotopy theory, you would support homotopy theory being in Category:Fiber bundles, because fiber bundles prove things about homotopy theory. However, the prevailing, and logical, trend is in fact the reverse inclusion, for this exact reason. So there is some argument for surgery theory being part of Category:Homotopy theory — and in fact it is part of Category:Algebraic topology, so it seems that this is indeed the right instinct. Ryan Reich (talk) 15:23, 8 December 2008 (UTC)
- Fibre bundles are used to calculate homotopy groups just as covering maps are used to calculate fundamental groups so I agree with you. But homotopy groups can also be used to study fibre bundles (one simple theorem that perhaps mildly indicates this is that any fibre bundle over a contractible space must be trivial (because a contractible space is homotopy equivalent to a point)). Topology Expert (talk) 20:14, 8 December 2008 (UTC)
It looks as though User:Ranicki has undone a few of my changes, adding things like Manifold and Lens space back to Category:Surgery theory. To me, this seems like overcategorization, as discussed above. I am going to again remove things from the category which do not belong there. siℓℓy rabbit (talk) 15:20, 14 December 2008 (UTC)
- I should think that manifold be added to that category (but not Lens space). Maybe bring up the issue on User:Ranicki's talk page and get his opinion first (and point him to this discussion). Topology Expert (talk) 15:29, 14 December 2008 (UTC)
- Manifold is already in multiple supercategories of surgery theory like Category:Geometric topology. It is clearly not appropriate for the surgery theory category. While surgery theory does use manifolds, manifolds are not part of surgery theory. Rather, they are part of geometric topology. siℓℓy rabbit (talk) 15:54, 14 December 2008 (UTC)
- I have removed several seemingly-inappropriate articles from Category:Surgery theory. Ozob (talk) 01:22, 16 December 2008 (UTC)
Commutative diagram[edit]
I have never drawn commutative diagrams on a computer. The article commutative diagram contains pictures but no LaTeX. Could someone help me make the commutative diagram expressing the naturality of the Mayer-Vietoris sequence? Thanks, GeometryGirl (talk) 20:53, 13 December 2008 (UTC)
- In LaTeX, for simple commutative diagrams, I generally use the amscd package, and for anything complicated I use the xymatrix command that is part xypic (and for more packages you can check out Milne's guide [11]). I'm not actually sure if any of these are available on wiki, and I'd like to know. Does anyone know? Recently, when I had to make a commutative diagram ([12]), I wrote it up in a separate place and made a png out of it, so if you tell me what the diagram is I could do that again. But I'm pretty curious to know whether one can just include packages in wiki. RobHar (talk) 21:26, 13 December 2008 (UTC)
- Well, let's try it:
- Failed to parse (unknown function "\usepackage"): {\displaystyle \usepackage{xy}\xymatrix{1 & 0 \\ 0 & 1}}
- Nor does the plain TeX approach work:
- Failed to parse (unknown function "\input"): {\displaystyle \input xy\xymatrix{1 & 0 \\ 0 & 1}}
- So no. It'd be nice, though. Ozob (talk) 00:38, 14 December 2008 (UTC)
- Well, let's try it:
I've just cut and pasted the follwoing from one of my LaTeX 2e files. It works perfectly well on there:
Failed to parse (unknown function "\begin{CD}"): {\displaystyle \begin{CD} R^2 \times R^3 @>\pi_1 >>R^3 @> f >> R \\ @V (A,B) VV @V B VV @VV \mbox{id} V \\ U \times S^2 \times I @>\pi_2 >> S^2 \times I @> g >> R \end{CD} } Δεκλαν Δαφισ (talk) 18:17, 18 December 2008 (UTC)
- Right, so here's the deal. You can't use any LaTeX environments on Wikipedia, except align (and it doesn't produce an equation number, so it's really align*). You can't load any packages, and only amsmath and amssymb are loaded for you. You can't use any of the programming facilities of TeX, nor any of the advanced spacing commands or any spacing command that implicitly or explicitly relies on the assumption that the "document" is a printed page with paragraphs and lines. You are always in math mode, although thankfully you can use the \text command. The only thing that the <math>...</math> environment here gives you is the ability to typeset bog-standard linear mathematical expressions.
- If you want commutative diagrams, I have had success using matrices; see Beauville-Laszlo theorem for an example. For anything complicated, just do it at home and upload the picture; see Homotopy category of chain complexes for examples. Ryan Reich (talk) 19:09, 18 December 2008 (UTC)
Strange edit on Talk:Wallpaper group[edit]
The "new user" User:Point-set topologist has added Wallpaper group to the category of mathematics Featured Articles, despite the fact that it seems not to be a featured article. It seems to me that this is a mistake; could someone more familiar with the GA/FA procedures confirm this? Plclark (talk) 22:22, 17 December 2008 (UTC)
- I just thought that the article should be rated a little higher; especially because of its size. Point-set topologist (talk) 10:33, 18 December 2008 (UTC)
- I undid the edit because I'm pretty sure that the article is not a featured article. But we'll see what happens. RobHar (talk) 22:55, 17 December 2008 (UTC)
- I've updated, signed, and dated the rating. Any editor should feel free to replace my assessment if they disagree. Geometry guy 23:04, 17 December 2008 (UTC)
- Your rating looks ok to me. Pictures are good in general, but there's far too little explanation of what most of them are pictures of. —David Eppstein (talk) 23:28, 17 December 2008 (UTC)
- Are we now using C-class for the rating or not? I got the impression from Wikipedia talk:WikiProject Mathematics/Archive 43#Overhaul of assessment and project banner, at the bottom, that we're not. -- Jitse Niesen (talk) 23:37, 17 December 2008 (UTC)
- This is a good question. In this case, I felt it was a little insulting to rate the article as Start class. I am (very) reluctantly coming round to the idea that we should drop our idiosyncratic Bplus, and take on C. Geometry guy 23:50, 17 December 2008 (UTC)
- Looks like I at least did something useful there by notifying people of that inaccurate rating. —Preceding unsigned comment added by Point-set topologist (talk • contribs) 10:34, 18 December 2008 (UTC)
- This is a good question. In this case, I felt it was a little insulting to rate the article as Start class. I am (very) reluctantly coming round to the idea that we should drop our idiosyncratic Bplus, and take on C. Geometry guy 23:50, 17 December 2008 (UTC)
- Are we now using C-class for the rating or not? I got the impression from Wikipedia talk:WikiProject Mathematics/Archive 43#Overhaul of assessment and project banner, at the bottom, that we're not. -- Jitse Niesen (talk) 23:37, 17 December 2008 (UTC)
- Your rating looks ok to me. Pictures are good in general, but there's far too little explanation of what most of them are pictures of. —David Eppstein (talk) 23:28, 17 December 2008 (UTC)
- I've updated, signed, and dated the rating. Any editor should feel free to replace my assessment if they disagree. Geometry guy 23:04, 17 December 2008 (UTC)
Are we now using C-class?[edit]
- Copied from above
Are we now using C-class for the rating or not? I got the impression from Wikipedia talk:WikiProject Mathematics/Archive 43#Overhaul of assessment and project banner, at the bottom, that we're not. -- Jitse Niesen (talk) 23:37, 17 December 2008 (UTC)
- This is a good question. In this case, I felt it was a little insulting to rate the article as Start class. I am (very) reluctantly coming round to the idea that we should drop our idiosyncratic Bplus, and take on C. Geometry guy 23:50, 17 December 2008 (UTC)
- Likewise I think transition to C-class would probably be a good idea. The existance of Bplus was my original idea: used to mark articles very close to being GA. I now think consistancy with the rest of wikipedia is probably has more benfit. --Salix (talk): 16:44, 18 December 2008 (UTC)
- I think consistency with the rest of Wikipedia is vastly overrated, but I don't mind the idea of C-class. CRGreathouse (t | c) 22:51, 18 December 2008 (UTC)
- I too think that having a C-class rating for math articles is a good idea, not necessarily because of consistency with other wikiprojects (although there is some value in that), but because in my observations many math articles actually do properly fall somewhere between start and B classes. Nsk92 (talk) 23:00, 18 December 2008 (UTC)
- Likewise I think transition to C-class would probably be a good idea. The existance of Bplus was my original idea: used to mark articles very close to being GA. I now think consistancy with the rest of wikipedia is probably has more benfit. --Salix (talk): 16:44, 18 December 2008 (UTC)





















![{\displaystyle \mathbf {Z} [{\sqrt {-5}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff18a58b48d228e03878fada8601ee4cc78fa617)