Deltahedron

From Wikipedia, the free encyclopedia
(Redirected from Deltahedra)
Not to be confused with Deltohedron.
The largest strictly convex deltahedron is the regular icosahedron.
The (Archimedean) truncated tetrahedron with its hexagons subdivided into triangles. This figure is not a strictly convex deltahedron, since coplanar (adjacent) faces are not allowed within the definition.

In geometry, a deltahedron (plural deltahedra) is a polyhedron whose faces are all (congruent) equilateral triangles. The name is taken from the Greek upper case delta letter (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra. By the handshaking lemma, each deltahedron has an even number of faces. Only eight deltahedra are strictly convex; these have 4, 6, 8, 10, 12, 14, 16, and 20 faces.[1] These eight deltahedra, with their respective numbers of faces, edges, and vertices, are listed below.

The eight strictly convex deltahedra[edit]

There are eight strictly convex deltahedra: three are regular polyhedra and Platonic solids, five are Johnson solids.

Regular strictly convex deltahedra
Image Name Faces Edges Vertices Vertex configurations Symmetry group
Tetrahedron 4 6 4 4 × 33 Td, [3,3]
Octahedron 8 12 6 6 × 34 Oh, [4,3]
Icosahedron 20 30 12 12 × 35 Ih, [5,3]
Non-regular strictly convex deltahedra
Image Name Faces Edges Vertices Vertex configurations Symmetry group
Triangular bipyramid 6 9 5 2 × 33
3 × 34		 D3h, [3,2]
Pentagonal bipyramid 10 15 7 5 × 34
2 × 35		 D5h, [5,2]
Snub disphenoid 12 18 8 4 × 34
4 × 35		 D2d, [4,2+]
Triaugmented triangular prism 14 21 9 3 × 34
6 × 35		 D3h, [3,2]
Gyroelongated square bipyramid 16 24 10 2 × 34
8 × 35		 D4d, [8,2+]

In the 6-faced deltahedron, some vertices have degree 3 and some degree 4. In the 10-, 12-, 14-, and 16-faced deltahedra, some vertices have degree 4 and some degree 5. These five non-regular deltahedra belong to the class of Johnson solids: non-uniform strictly convex polyhedra with regular polygons for faces.

A deltahedron retains its shape: even if its edges are free to rotate around their vertices (so that the angles between them are fluid), they don't move. Not all polyhedra have this property: for example, if some of the angles of a cube are relaxed, it can be deformed into a non-right square prism or even into a rhombohedron with no right angle at all.

There is no 18-faced strictly convex deltahedron.[2] However, the edge-contracted icosahedron gives an example of an octadecahedron that can either be made strictly convex with 18 irregular triangular faces, or made equilateral[3] with 18 (regular) triangular faces that include two sets of three coplanar triangles.

Non-strictly convex cases[edit]

There are infinitely many cases with coplanar triangles, allowing for sections of the infinite triangular tiling. If the sets of coplanar triangles are considered a single face, a smaller set of faces, edges, and vertices can be counted. The coplanar triangular faces can be merged into rhombic, trapezoidal, hexagonal, or other polygonal faces. Each face must be a convex polyiamond, such as , , , , , , , , ...[4]

Some small examples include:

Deltahedra with coplanar faces
Image Name Faces Edges Vertices Vertex configurations Symmetry group
Augmented octahedron
Augmentation
1 tet + 1 oct 		10 15 7 1 × 33
3 × 34
3 × 35
0 × 36 		C3v, [3]
4
3 		12
Trigonal trapezohedron
Augmentation
2 tets + 1 oct 		12 18 8 2 × 33
0 × 34
6 × 35
0 × 36 		D3d, [6,2+]
6 12
Augmentation
2 tets + 1 oct 		12 18 8 2 × 33
1 × 34
4 × 35
1 × 36 		C2v, [2]
2
2
2 		11 7
Triangular frustum
Augmentation
3 tets + 1 oct 		14 21 9 3 × 33
0 × 34
3 × 35
3 × 36 		C3v, [3]
1
3
1 		9 6
Elongated octahedron
Augmentation
2 tets + 2 octs 		16 24 10 0 × 33
4 × 34
4 × 35
2 × 36 		D2h, [2,2]
4
4 		12 6
Tetrahedron
Augmentation
4 tets + 1 oct 		16 24 10 4 × 33
0 × 34
0 × 35
6 × 36 		Td, [3,3]
4 6 4
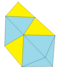
Augmentation
3 tets + 2 octs 		18 27 11 1 × 33
2 × 34
5 × 35
3 × 36 		{Id,R}
where R is a reflection through a plane
2
1
2
2 		14 9
Edge-contracted icosahedron 18 27 11 0 × 33
2 × 34
8 × 35
1 × 36 		C2v, [2]
12
2 		22 10
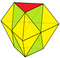
Triangular bifrustum
Augmentation
6 tets + 2 octs 		20 30 12 0 × 33
3 × 34
6 × 35
3 × 36 		D3h, [3,2]
2
6 		15 9
Triangular cupola
Augmentation
4 tets + 3 octs 		22 33 13 0 × 33
3 × 34
6 × 35
4 × 36 		C3v, [3]
3
3
1
1 		15 9
Triangular bipyramid
Augmentation
8 tets + 2 octs 		24 36 14 2 × 33
3 × 34
0 × 35
9 × 36 		D3h, [3,2]
6 9 5
Hexagonal antiprism 24 36 14 0 × 33
0 × 34
12 × 35
2 × 36 		D6d, [12,2+]
12
2 		24 12
Truncated tetrahedron
Augmentation
6 tets + 4 octs 		28 42 16 0 × 33
0 × 34
12 × 35
4 × 36 		Td, [3,3]
4
4 		18 12
Tetrakis cuboctahedron
Octahedron
Augmentation
8 tets + 6 octs 		32 48 18 0 × 33
12 × 34
0 × 35
6 × 36 		Oh, [4,3]
8 12 6

Non-convex forms[edit]

There are an infinite number of non-convex deltahedra.

Five non-convex deltahedra can be generated by adding an equilateral pyramid to every face of a Platonic solid:

Equilateral pyramid-augmented Platonic solids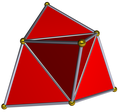
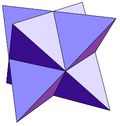
triakis tetrahedron tetrakis hexahedron triakis octahedron
(stella octangula) 		pentakis dodecahedron triakis icosahedron
12 triangles 24 triangles 60 triangles

Other non-convex deltahedra can be generated by assembling several regular tetrahedra:

Some non-convex equilateral augmented tetrahedra
8 triangles 10 triangles 12 triangles

Like all toroidal polyhedra, toroidal deltahedra are non-convex; example:


A toroidal deltahedron
48 triangles

When possible, adding an inverted equilateral pyramid to every face of a polyhedron makes a non-convex deltahedron; example:


Excavated dodecahedron
60 triangles

Like all self-intersecting polyhedra, self-intersecting deltahedra are non-convex; example: Great icosahedron — a Kepler-Poinsot solid, with 20 intersecting triangles:

See also[edit]

References[edit]

  1. ^ Freudenthal, H; van der Waerden, B. L. (1947), "Over een bewering van Euclides ("On an Assertion of Euclid")", Simon Stevin (in Dutch), 25: 115–128 (They showed that there are just eight strictly convex deltahedra.)
  2. ^ Trigg, Charles W. (1978), "An Infinite Class of Deltahedra", Mathematics Magazine, 51 (1): 55–57, doi:10.1080/0025570X.1978.11976675, JSTOR 2689647.
  3. ^ Weisstein, Eric W. "Equilateral Polyhedron". mathworld.wolfram.com. Retrieved 2024-05-27.
  4. ^ The Convex Deltahedra And the Allowance of Coplanar Faces

Further reading[edit]

  • Rausenberger, O. (1915), "Konvexe pseudoreguläre Polyeder", Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht, 46: 135–142.
  • Cundy, H. Martyn (December 1952), "Deltahedra", Mathematical Gazette, 36: 263–266, doi:10.2307/3608204, JSTOR 3608204.
  • Cundy, H. Martyn; Rollett, A. (1989), "3.11. Deltahedra", Mathematical Models (3rd ed.), Stradbroke, England: Tarquin Pub., pp. 142–144.
  • Gardner, Martin (1992), Fractal Music, Hypercards, and More: Mathematical Recreations from Scientific American, New York: W. H. Freeman, pp. 40, 53, and 58–60.
  • Pugh, Anthony (1976), Polyhedra: A visual approach, California: University of California Press Berkeley, ISBN 0-520-03056-7, pp. 35–36.

External links[edit]

Retrieved from "https://en.wikipedia.org/w/index.php?title=Deltahedron&oldid=1226008904"