Sorted array

Sorted array
Type	Array
Invented	1945
Invented by	John von Neumann
Time complexity in big O notation Operation Average Worst case Search O(log n) O(log n) Insert O(n) O(n) Delete O(n) O(n) Space complexity Space O(n) O(n)

A sorted array is an array data structure in which each element is sorted in numerical, alphabetical, or some other order, and placed at equally spaced addresses in computer memory. It is typically used in computer science to implement static lookup tables to hold multiple values which have the same data type. Sorting an array is useful in organising data in ordered form and recovering them rapidly.

Methods

There are many well-known methods by which an array can be sorted, which include, but are not limited to: Selection sort, Bubble sort, Insertion sort, Merge sort, Quicksort, Heapsort, and Counting sort. These sorting techniques have different algorithms associated with them, and there are therefore different advantages to using each method.

Overview

Sorted arrays are the most space-efficient data structure with the best locality of reference for sequentially stored data.

Elements within a sorted array are found using a binary search, in O(log n); thus sorted arrays are suited for cases when one needs to be able to look up elements quickly, e.g. as a set or multiset data structure. This complexity for lookups is the same as for self-balancing binary search trees.

In some data structures, an array of structures is used. In such cases, the same sorting methods can be used to sort the structures according to some key as a structure element; for example, sorting records of students according to roll numbers or names or grades.

If one is using a sorted dynamic array, then it is possible to insert and delete elements. The insertion and deletion of elements in a sorted array executes at O(n), due to the need to shift all the elements following the element to be inserted or deleted; in comparison a self-balancing binary search tree inserts and deletes at O(log n). In the case where elements are deleted or inserted at the end, a sorted dynamic array can do this in amortized O(1) time while a self-balancing binary search tree always operates at O(log n).

Elements in a sorted array can be looked up by their index (random access) at O(1) time, an operation taking O(log n) or O(n) time for more complex data structures.

History

John von Neumann wrote the first array sorting program (merge sort) in 1945, when the first stored-program computer was still being built.

Applications of sorted arrays

Commercial computing

Government organizations, private companies and many web-based applications have to deal with huge amounts of data. The data will often have to be accessed multiple times. Keeping the data in a sorted format allows for quick and easy retrieval.

In discrete mathematics

Sorted arrays can be used to implement Dijkstra's algorithm or Prim's algorithm. Also, algorithms like Kruskal's algorithm for finding minimal spanning trees.

In priority scheduling

At the operating system level, many processes are pending at a time but the can handle only one process at a single instance in time. Therefore, priorities are associated to each process. Then the processes are sent to the CPU according to the highest priority by using sorted array of process IDs. Here, processes got sorted depending upon their priorities and then CPU is allocated to them. The process having the highest priority takes first position in sorted array. Hence priority-wise system processes scheduling is done.

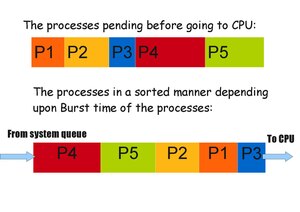
In shortest-job-first scheduling

This is the special case of priority scheduling. Here, processes get sorted according to burst time of the processes. The process requiring the shortest time will be allocated CPU first. Hence, processes are being sent to CPU according to their burst time.

Process	Burst time
P1	3
P2	4
P3	1
P4	8
P5	6

See also

• Sorting algorithm
• Binary search algorithm
• Heap (data structure)
• Search data structure