Formula for the area of a quadrilateral
A quadrilateral. In geometry , Bretschneider's formula is a mathematical expression for the area of a general quadrilateral .
It works on both convex and concave quadrilaterals (but not crossed ones), whether it is cyclic or not.
The German mathematician Carl Anton Bretschneider discovered the formula in 1842. The formula was also derived in the same year by the German mathematician Karl Georg Christian von Staudt .
Bretschneider's formula is expressed as:
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
a
b
c
d
⋅
cos
2
(
α
+
γ
2
)
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cdot \cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)}}}
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
1
2
a
b
c
d
[
1
+
cos
(
α
+
γ
)
]
.
{\displaystyle ={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{2}}abcd[1+\cos(\alpha +\gamma )]}}.}
Here, a b c d s semiperimeter , and α γ
cos
(
α
+
γ
)
=
cos
(
β
+
δ
)
{\displaystyle \cos(\alpha +\gamma )=\cos(\beta +\delta )}
α
+
β
+
γ
+
δ
=
360
∘
.
{\displaystyle \alpha +\beta +\gamma +\delta =360^{\circ }.}
Denote the area of the quadrilateral by K
K
=
a
d
sin
α
2
+
b
c
sin
γ
2
.
{\displaystyle {\begin{aligned}K&={\frac {ad\sin \alpha }{2}}+{\frac {bc\sin \gamma }{2}}.\end{aligned}}}
Therefore
2
K
=
(
a
d
)
sin
α
+
(
b
c
)
sin
γ
.
{\displaystyle 2K=(ad)\sin \alpha +(bc)\sin \gamma .}
4
K
2
=
(
a
d
)
2
sin
2
α
+
(
b
c
)
2
sin
2
γ
+
2
a
b
c
d
sin
α
sin
γ
.
{\displaystyle 4K^{2}=(ad)^{2}\sin ^{2}\alpha +(bc)^{2}\sin ^{2}\gamma +2abcd\sin \alpha \sin \gamma .}
The law of cosines implies that
a
2
+
d
2
−
2
a
d
cos
α
=
b
2
+
c
2
−
2
b
c
cos
γ
,
{\displaystyle a^{2}+d^{2}-2ad\cos \alpha =b^{2}+c^{2}-2bc\cos \gamma ,}
because both sides equal the square of the length of the diagonal BD
(
a
2
+
d
2
−
b
2
−
c
2
)
2
4
=
(
a
d
)
2
cos
2
α
+
(
b
c
)
2
cos
2
γ
−
2
a
b
c
d
cos
α
cos
γ
.
{\displaystyle {\frac {(a^{2}+d^{2}-b^{2}-c^{2})^{2}}{4}}=(ad)^{2}\cos ^{2}\alpha +(bc)^{2}\cos ^{2}\gamma -2abcd\cos \alpha \cos \gamma .}
Adding this to the above formula for 4K 2 yields
4
K
2
+
(
a
2
+
d
2
−
b
2
−
c
2
)
2
4
=
(
a
d
)
2
+
(
b
c
)
2
−
2
a
b
c
d
cos
(
α
+
γ
)
=
(
a
d
+
b
c
)
2
−
2
a
b
c
d
−
2
a
b
c
d
cos
(
α
+
γ
)
=
(
a
d
+
b
c
)
2
−
2
a
b
c
d
(
cos
(
α
+
γ
)
+
1
)
=
(
a
d
+
b
c
)
2
−
4
a
b
c
d
(
cos
(
α
+
γ
)
+
1
2
)
=
(
a
d
+
b
c
)
2
−
4
a
b
c
d
cos
2
(
α
+
γ
2
)
.
{\displaystyle {\begin{aligned}4K^{2}+{\frac {(a^{2}+d^{2}-b^{2}-c^{2})^{2}}{4}}&=(ad)^{2}+(bc)^{2}-2abcd\cos(\alpha +\gamma )\\&=(ad+bc)^{2}-2abcd-2abcd\cos(\alpha +\gamma )\\&=(ad+bc)^{2}-2abcd(\cos(\alpha +\gamma )+1)\\&=(ad+bc)^{2}-4abcd\left({\frac {\cos(\alpha +\gamma )+1}{2}}\right)\\&=(ad+bc)^{2}-4abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).\end{aligned}}}
Note that:
cos
2
α
+
γ
2
=
1
+
cos
(
α
+
γ
)
2
{\displaystyle \cos ^{2}{\frac {\alpha +\gamma }{2}}={\frac {1+\cos(\alpha +\gamma )}{2}}}
α
+
γ
2
{\displaystyle {\frac {\alpha +\gamma }{2}}}
Following the same steps as in Brahmagupta's formula , this can be written as
16
K
2
=
(
a
+
b
+
c
−
d
)
(
a
+
b
−
c
+
d
)
(
a
−
b
+
c
+
d
)
(
−
a
+
b
+
c
+
d
)
−
16
a
b
c
d
cos
2
(
α
+
γ
2
)
.
{\displaystyle 16K^{2}=(a+b+c-d)(a+b-c+d)(a-b+c+d)(-a+b+c+d)-16abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right).}
Introducing the semiperimeter
s
=
a
+
b
+
c
+
d
2
,
{\displaystyle s={\frac {a+b+c+d}{2}},}
the above becomes
16
K
2
=
16
(
s
−
d
)
(
s
−
c
)
(
s
−
b
)
(
s
−
a
)
−
16
a
b
c
d
cos
2
(
α
+
γ
2
)
{\displaystyle 16K^{2}=16(s-d)(s-c)(s-b)(s-a)-16abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)}
K
2
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
a
b
c
d
cos
2
(
α
+
γ
2
)
{\displaystyle K^{2}=(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)}
and Bretschneider's formula follows after taking the square root of both sides:
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
a
b
c
d
⋅
cos
2
(
α
+
γ
2
)
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cdot \cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)}}}
The second form is given by using the cosine half-angle identity
cos
2
(
α
+
γ
2
)
=
1
+
cos
(
α
+
γ
)
2
,
{\displaystyle \cos ^{2}\left({\frac {\alpha +\gamma }{2}}\right)={\frac {1+\cos \left(\alpha +\gamma \right)}{2}},}
yielding
K
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
1
2
a
b
c
d
[
1
+
cos
(
α
+
γ
)
]
.
{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{2}}abcd[1+\cos(\alpha +\gamma )]}}.}
Emmanuel García has used the generalized half angle formulas to give an alternative proof. [ 1]
Bretschneider's formula generalizes Brahmagupta's formula for the area of a cyclic quadrilateral , which in turn generalizes Heron's formula for the area of a triangle .
The trigonometric adjustment in Bretschneider's formula for non-cyclicality of the quadrilateral can be rewritten non-trigonometrically in terms of the sides and the diagonals e f [ 2] [ 3]
K
=
1
4
4
e
2
f
2
−
(
b
2
+
d
2
−
a
2
−
c
2
)
2
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
1
4
(
(
a
c
+
b
d
)
2
−
e
2
f
2
)
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
(
s
−
d
)
−
1
4
(
a
c
+
b
d
+
e
f
)
(
a
c
+
b
d
−
e
f
)
{\displaystyle {\begin{aligned}K&={\tfrac {1}{4}}{\sqrt {4e^{2}f^{2}-(b^{2}+d^{2}-a^{2}-c^{2})^{2}}}\\&={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{4}}((ac+bd)^{2}-e^{2}f^{2})}}\\&={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{4}}(ac+bd+ef)(ac+bd-ef)}}\\\end{aligned}}}
[ edit ] Ayoub, Ayoub B. (2007). "Generalizations of Ptolemy and Brahmagupta Theorems". Mathematics and Computer Education . 41 (1). ISSN 0730-8639 . C. A. Bretschneider. Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes. Archiv der Mathematik und Physik, Band 2, 1842, S. 225-261 (online copy, German )
F. Strehlke: Zwei neue Sätze vom ebenen und sphärischen Viereck und Umkehrung des Ptolemaischen Lehrsatzes . Archiv der Mathematik und Physik, Band 2, 1842, S. 323-326 (online copy, German ) 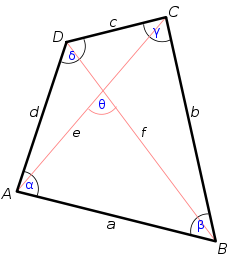


![{\displaystyle ={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{2}}abcd[1+\cos(\alpha +\gamma )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274a2fdb98ed6e71c98f8dee380c3e1318d9e4a7)















![{\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{2}}abcd[1+\cos(\alpha +\gamma )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd67344e861ae283f212781cbefdb9355576d99a)
