Directivity
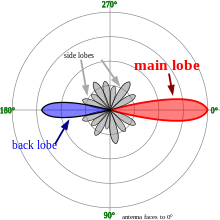
In electromagnetics, directivity is a parameter of an antenna or optical system which measures the degree to which the radiation emitted is concentrated in a single direction. It is the ratio of the radiation intensity in a given direction from the antenna to the radiation intensity averaged over all directions.[1] Therefore, the directivity of a hypothetical isotropic radiator, a source of electromagnetic waves which radiates the same power in all directions, is 1, or 0 dBi.
An antenna's directivity is greater than its gain by an efficiency factor, radiation efficiency.[1] Directivity is an important measure because many antennas and optical systems are designed to radiate electromagnetic waves in a single direction or over a narrow-angle. By the principle of reciprocity, the directivity of an antenna when receiving is equal to its directivity when transmitting.
The directivity of an actual antenna can vary from 1.76 dBi for a short dipole to as much as 50 dBi for a large dish antenna.[2]
Definition
[edit]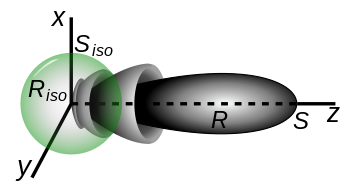
| Part of a series on |
| Antennas |
|---|
 |
The directivity, , of an antenna is defined for all incident angles of an antenna. The term "directive gain" is deprecated by IEEE. If an angle relative to the antenna is not specified, then directivity is presumed to refer to the axis of maximum radiation intensity.[1]
Here and are the zenith angle and azimuth angle respectively in the standard spherical coordinate angles; is the radiation intensity, which is the power per unit solid angle; and is the total radiated power. The quantities and satisfy the relation
that is, the total radiated power is the power per unit solid angle integrated over a spherical surface. Since there are 4π steradians on the surface of a sphere, the quantity represents the average power per unit solid angle.
In other words, directivity is the radiation intensity of an antenna at a particular coordinate combination divided by what the radiation intensity would have been had the antenna been an isotropic antenna radiating the same amount of total power into space.
Directivity, if a direction is not specified, is the maximal directive gain value found among all possible solid angles:
In antenna arrays
[edit]In an antenna array the directivity is a complicated calculation in the general case. For a linear array the directivity will always be less than or equal to the number of elements. For a standard linear array (SLA), where the element spacing is , the directivity is equal to the inverse of the square of the 2-norm of the array weight vector, under the assumption that the weight vector is normalized such that its sum is unity.[3]
In the case of a uniformly weighted (un-tapered) SLA, this reduces to simply N, the number of array elements.
For a planar array, the computation of directivity is more complicated and requires consideration of the positions of each array element with respect to all the others and with respect to wavelength.[4] For a planar rectangular or hexagonally spaced array with non-isotropic elements, the maximum directivity can be estimated using the universal ratio of effective aperture to directivity, ,
where dx and dy are the element spacings in the x and y dimensions and is the "illumination efficiency" of the array that accounts for tapering and spacing of the elements in the array. For an un-tapered array with elements at less than spacing, . Note that for an un-tapered standard rectangular array (SRA), where , this reduces to . For an un-tapered standard rectangular array (SRA), where , this reduces to a maximum value of . The directivity of a planar array is the product of the array gain, and the directivity of an element (assuming all of the elements are identical) only in the limit as element spacing becomes much larger than lambda. In the case of a sparse array, where element spacing , is reduced because the array is not uniformly illuminated.
There is a physically intuitive reason for this relationship; essentially there are a limited number of photons per unit area to be captured by the individual antennas. Placing two high gain antennas very close to each other (less than a wavelength) does not buy twice the gain, for example. Conversely, if the antenna are more than a wavelength apart, there are photons that fall between the elements and are not collected at all. This is why the physical aperture size must be taken into account.
Let's assume a 16×16 un-tapered standard rectangular array (which means that elements are spaced at .) The array gain is dB. If the array were tapered, this value would go down. The directivity, assuming isotropic elements, is 25.9dBi.[5] Now assume elements with 9.0dBi directivity. The directivity is not 33.1dBi, but rather is only 29.2dBi.[6] The reason for this is that the effective aperture of the individual elements limits their directivity. So, . Note, in this case because the array is un-tapered. Why the slight difference from 29.05 dBi? The elements around the edge of the array aren't as limited in their effective aperture as are the majority of elements.
Now let's move the array elements to spacing. From the above formula, we expect the directivity to peak at . The actual result is 34.6380 dBi, just shy of the ideal 35.0745 dBi we expected.[7] Why the difference from the ideal? If the spacing in the x and y dimensions is , then the spacing along the diagonals is , thus creating tiny regions in the overall array where photons are missed, leading to .
Now go to spacing. The result now should converge to N times the element gain, or + 9 dBi = 33.1 dBi. The actual result is in fact, 33.1 dBi.[8]
For antenna arrays, the closed form expression for Directivity for progressively phased [9] array of isotropic sources will be given by,[10]
where,
- is the total number of elements on the aperture;
- represents the location of elements in Cartesian co-ordinate system;
- is the complex excitation coefficient of the -element;
- is the phase component (progressive phasing);
- is the wavenumber;
- is the angular location of the far-field target;
- is the Euclidean distance between the and element on the aperture, and
Further studies on directivity expressions for various cases, like if the sources are omnidirectional (even in the array environment) like if the prototype element-pattern takes the form , and not restricting to progressive phasing can be done from.[11][12][10][13]
Relation to beam width
[edit]The beam solid angle, represented as , is defined as the solid angle which all power would flow through if the antenna radiation intensity were constant at its maximal value. If the beam solid angle is known, then maximum directivity can be calculated as
which simply calculates the ratio of the beam solid angle to the solid angle of a sphere.
The beam solid angle can be approximated for antennas with one narrow major lobe and very negligible minor lobes by simply multiplying the half-power beamwidths (in radians) in two perpendicular planes. The half-power beamwidth is simply the angle in which the radiation intensity is at least half of the peak radiation intensity.
The same calculations can be performed in degrees rather than in radians:
where is the half-power beamwidth in one plane (in degrees) and is the half-power beamwidth in a plane at a right angle to the other (in degrees).
In planar arrays, a better approximation is
For an antenna with a conical (or approximately conical) beam with a half-power beamwidth of degrees, then elementary integral calculus yields an expression for the directivity as
- .
Expression in decibels
[edit]The directivity is rarely expressed as the unitless number but rather as a decibel comparison to a reference antenna:
The reference antenna is usually the theoretical perfect isotropic radiator, which radiates uniformly in all directions and hence has a directivity of 1. The calculation is therefore simplified to
Another common reference antenna is the theoretical perfect half-wave dipole, which radiates perpendicular to itself with a directivity of 1.64:
Accounting for polarization
[edit]When polarization is taken under consideration, three additional measures can be calculated:
Partial directive gain
[edit]Partial directive gain is the power density in a particular direction and for a particular component of the polarization, divided by the average power density for all directions and all polarizations. For any pair of orthogonal polarizations (such as left-hand-circular and right-hand-circular), the individual power densities simply add to give the total power density. Thus, if expressed as dimensionless ratios rather than in dB, the total directive gain is equal to the sum of the two partial directive gains.[14]
Partial directivity
[edit]Partial directivity is calculated in the same manner as the partial directive gain, but without consideration of antenna efficiency (i.e. assuming a lossless antenna). It is similarly additive for orthogonal polarizations.
Partial gain
[edit]Partial gain is calculated in the same manner as gain, but considering only a certain polarization. It is similarly additive for orthogonal polarizations.
In other areas
[edit]The term directivity is also used with other systems.
With directional couplers, directivity is a measure of the difference in dB of the power output at a coupled port, when power is transmitted in the desired direction, to the power output at the same coupled port when the same amount of power is transmitted in the opposite direction.[15]
In acoustics, it is used as a measure of the radiation pattern from a source indicating how much of the total energy from the source is radiating in a particular direction. In electro-acoustics, these patterns commonly include omnidirectional, cardioid and hyper-cardioid microphone polar patterns. A loudspeaker with a high degree of directivity (narrow dispersion pattern) can be said to have a high Q.[16]
See also
[edit]References
[edit]- ^ a b c IEEE Std 145-2013, IEEE Standard for Definitions of Terms for Antennas, IEEE
- ^ Antenna Tutorial
- ^ Van Trees, H.L. Optimum Array Processing. pp. 60–63.
- ^ Van Trees, H.L. Optimum Array Processing. pp. 247–249.
- ^ Van Trees, H.L. Optimum Array Processing. pp. 247–249.
- ^ "MATLAB Phased Array System Toolbox".
- ^ "MATLAB Phased Array System Toolbox".
- ^ "MATLAB Phased Array System Toolbox".
- ^ "Phased Array Antennas: Floquet Analysis, Synthesis, BFNs and Active Array Systems | Wiley". Wiley.com. Retrieved 2022-05-29.
- ^ a b Das, Sudipta; Mandal, Durbadal; Ghoshal, Sakti Prasad; Kar, Rajib (February 2017). "Generalization of Directivity Expressions for Antenna Arrays". IEEE Transactions on Antennas and Propagation. 65 (2): 915–919. Bibcode:2017ITAP...65..915D. doi:10.1109/TAP.2016.2632738. ISSN 1558-2221. S2CID 19645584.
- ^ Das, Sudipta; Mandal, Durbadal; Kar, Rajib; Ghoshal, Sakti Prasad (July 2013). "A Generalized Closed Form Expression of Directivity of Arbitrary Planar Antenna Arrays". IEEE Transactions on Antennas and Propagation. 61 (7): 3909–3911. Bibcode:2013ITAP...61.3909D. doi:10.1109/TAP.2013.2257652. ISSN 1558-2221. S2CID 44492351.
- ^ Kedar, Ashutosh; Ligthart, L. P. (February 2019). "Wide Scanning Characteristics of Sparse Phased Array Antennas Using an Analytical Expression for Directivity". IEEE Transactions on Antennas and Propagation. 67 (2): 905–914. Bibcode:2019ITAP...67..905K. doi:10.1109/TAP.2018.2880006. ISSN 0018-926X. S2CID 59620334.
- ^ Costa, Bruno Felipe; Abrão, Taufik (December 2018). "Closed-Form Directivity Expression for Arbitrary Volumetric Antenna Arrays". IEEE Transactions on Antennas and Propagation. 66 (12): 7443–7448. arXiv:1810.01487. Bibcode:2018ITAP...66.7443C. doi:10.1109/TAP.2018.2869243. ISSN 1558-2221. S2CID 54196716.
- ^ Institute of Electrical and Electronics Engineers, “The IEEE standard dictionary of electrical and electronics terms”; 6th ed. New York, N.Y., Institute of Electrical and Electronics Engineers, c1997. IEEE Std 100-1996. ISBN 1-55937-833-6 [ed. Standards Coordinating Committee 10, Terms and Definitions; Jane Radatz, (chair)]
- ^ App note, Mini-Circuits directional couplers
- ^ AES Professional Audio Reference definition of Q
Further reading
[edit]- Coleman, Christopher (2004). "Basic Concepts". An Introduction to Radio Frequency Engineering. Cambridge University Press. ISBN 0-521-83481-3.












![{\displaystyle {\begin{aligned}D&=\max \left({\frac {U}{P_{\text{tot}}/\left(4\pi \right)}}\right)\\[3pt]&={\frac {\left.U(\theta ,\phi )\right|_{\text{max}}}{{\frac {1}{4\pi }}\int _{0}^{2\pi }\int _{0}^{\pi }U(\theta ,\phi )\sin \theta \,d\theta \,d\phi }}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d481307813f604f90cf6bdceecab79d968f35a0f)







































![{\displaystyle D_{\text{dB}}=10\log _{10}\left[{\frac {D}{D_{\text{reference}}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6591584599997f00e700aa3a4955c70c57c27c90)

![{\displaystyle D_{\text{dBd}}\approx 10\log _{10}\left[{\frac {D}{1.64}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c848521cbd3d51d8ec5b58198e851276af15a16)