Fermat's spiral


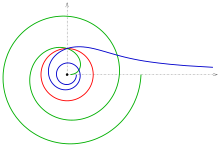
A Fermat's spiral or parabolic spiral is a plane curve with the property that the area between any two consecutive full turns around the spiral is invariant. As a result, the distance between turns grows in inverse proportion to their distance from the spiral center, contrasting with the Archimedean spiral (for which this distance is invariant) and the logarithmic spiral (for which the distance between turns is proportional to the distance from the center). Fermat spirals are named after Pierre de Fermat.[1]
Their applications include curvature continuous blending of curves,[1] modeling plant growth and the shapes of certain spiral galaxies, and the design of variable capacitors, solar power reflector arrays, and cyclotrons.
Coordinate representation[edit]
Polar[edit]
The representation of the Fermat spiral in polar coordinates (r, φ) is given by the equation
The two choices of sign give the two branches of the spiral, which meet smoothly at the origin. If the same variables were reinterpreted as Cartesian coordinates, this would be the equation of a parabola with horizontal axis, which again has two branches above and below the axis, meeting at the origin.
Cartesian[edit]
The Fermat spiral with polar equation
and the second one
They generate the points of branches of the curve as the parameter φ ranges over the positive real numbers.
For any (x, y) generated in this way, dividing x by y cancels the a√φ parts of the parametric equations, leaving the simpler equation x/y = cot φ. From this equation, substituting φ by φ = r2/a2 (a rearranged form of the polar equation for the spiral) and then substituting r by r = √x2 + y2 (the conversion from Cartesian to polar) leaves an equation for the Fermat spiral in terms of only x and y:
Geometric properties[edit]

Division of the plane[edit]
A complete Fermat's spiral (both branches) is a smooth double point free curve, in contrast with the Archimedean and hyperbolic spiral. Like a line or circle or parabola, it divides the plane into two connected regions.

Polar slope[edit]
From vector calculus in polar coordinates one gets the formula
for the polar slope and its angle α between the tangent of a curve and the corresponding polar circle (see diagram).
For Fermat's spiral r = a√φ one gets
Hence the slope angle is monotonely decreasing.
Curvature[edit]
From the formula
for the curvature of a curve with polar equation r = r(φ) and its derivatives
one gets the curvature of a Fermat's spiral:
At the origin the curvature is 0. Hence the complete curve has at the origin an inflection point and the x-axis is its tangent there.
Area between arcs[edit]
The area of a sector of Fermat's spiral between two points (r(φ1), φ1) and (r(φ2), φ2) is
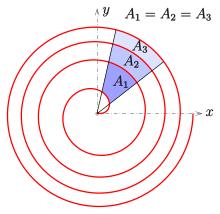
After raising both angles by 2π one gets
Hence the area A of the region between two neighboring arcs is
For the example shown in the diagram, all neighboring stripes have the same area: A1 = A2 = A3.
This property is used in electrical engineering for the construction of variable capacitors.[2]

Special case due to Fermat[edit]
In 1636, Fermat wrote a letter [3] to Marin Mersenne which contains the following special case:
Let φ1 = 0, φ2 = 2π; then the area of the black region (see diagram) is A0 = a2π2, which is half of the area of the circle K0 with radius r(2π). The regions between neighboring curves (white, blue, yellow) have the same area A = 2a2π2. Hence:
- The area between two arcs of the spiral after a full turn equals the area of the circle K0.
Arc length[edit]
The length of the arc of Fermat's spiral between two points (r(φi), φi) can be calculated by the integral:
This integral leads to an elliptical integral, which can be solved numerically.
The arc length of the positive branch of the Fermat's spiral from the origin can also be defined by hypergeometric functions 2F1(a, b; c; z) and the incomplete beta function B(z; a, b):[4]
Circle inversion[edit]
The inversion at the unit circle has in polar coordinates the simple description (r, φ) ↦ (1/r, φ).
- The image of Fermat's spiral r = a√φ under the inversion at the unit circle is a lituus spiral with polar equation When φ = 1/a2, both curves intersect at a fixed point on the unit circle.
- The tangent (x-axis) at the inflection point (origin) of Fermat's spiral is mapped onto itself and is the asymptotic line of the lituus spiral.
The golden ratio and the golden angle[edit]
In disc phyllotaxis, as in the sunflower and daisy, the mesh of spirals occurs in Fibonacci numbers because divergence (angle of succession in a single spiral arrangement) approaches the golden ratio. The shape of the spirals depends on the growth of the elements generated sequentially. In mature-disc phyllotaxis, when all the elements are the same size, the shape of the spirals is that of Fermat spirals—ideally. That is because Fermat's spiral traverses equal annuli in equal turns. The full model proposed by H. Vogel in 1979[5] is
where θ is the angle, r is the radius or distance from the center, and n is the index number of the floret and c is a constant scaling factor. The angle 137.508° is the golden angle which is approximated by ratios of Fibonacci numbers.[6]
The resulting spiral pattern of unit disks should be distinguished from the Doyle spirals, patterns formed by tangent disks of geometrically increasing radii placed on logarithmic spirals.
Solar plants[edit]
Fermat's spiral has also been found to be an efficient layout for the mirrors of concentrated solar power plants.[7]
See also[edit]
References[edit]
- ^ a b Lekkas, Anastasios M.; Dahl, Andreas R.; Breivik, Morten; Fossen, Thor I. (2013). "Continuous-Curvature Path Generation Using Fermat's Spiral" (PDF). Modeling, Identification and Control. 34 (4): 183–198. ISSN 1890-1328. Archived from the original (PDF) on 2020-10-28.
- ^ Wicke, Fritz (2013). Einführung in die höhere Mathematik. Springer-Verlag. p. 414. ISBN 978-3-662-36804-6.
- ^ Tannery, Paul (ed.). "Lettre de Fermat à Mersenne du 3 juin 1636". Œuvres de Fermat. Vol. 3. p. 277.
- ^ Weisstein, Eric W. "Fermat's Spiral". MathWorld. Retrieved 2023-02-04.
- ^ Vogel, H. (1979). "A better way to construct the sunflower head". Mathematical Biosciences. 44 (3–4): 179–189. doi:10.1016/0025-5564(79)90080-4.
- ^ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.
- ^ Noone, Corey J.; Torrilhon, Manuel; Mitsos, Alexander (December 2011). "Heliostat Field Optimization: A New Computationally Efficient Model and Biomimetic Layout". Solar Energy. 86 (2): 792–803. doi:10.1016/j.solener.2011.12.007.
Further reading[edit]
- Lawrence, J. Dennis (1972). A Catalog of Special Plane Curves. Dover Publications. pp. 31, 186. ISBN 0-486-60288-5.



















