File:Inclinedthrow.gif
Inclinedthrow.gif (400 × 288 pixels, file size: 374 KB, MIME type: image/gif, looped, 102 frames, 10 s)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 16:10, 21 October 2020 |  | 400 × 288 (374 KB) | Geek3 | adjusted friction coefficients such to make terminal velocity of both trajectories equal. In this case, the Newton projectile moves further. |
| 12:57, 21 October 2009 |  | 400 × 288 (453 KB) | AllenMcC. | added Newton drag | |
| 00:40, 22 December 2008 | 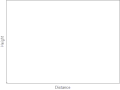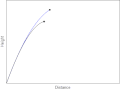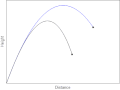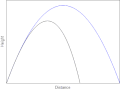 | 400 × 299 (393 KB) | AllenMcC. | == Summary == {{Information |Description={{en|1=Trajectories of two objects thrown at the same angle. The blue object doesn't experience any drag and moves along a parabola. The black object experiences Stokes' drag.}} |Source=Own work by uploader |Author | |
| 20:12, 18 December 2008 |  | 400 × 299 (393 KB) | AllenMcC. | == Summary == {{Information |Description={{en|1=Trajectories of two objects thrown at the same angle. The blue object doesn't experience any drag and moves along a parabola. The black object experiences Stokes' drag.}} |Source=Own work by uploader |Author | |
| 04:07, 15 December 2008 |  | 700 × 519 (636 KB) | AllenMcC. | {{Information |Description={{en|1=Trajectories of two objects thrown at the same angle. The blue object doesn't experience friction and moves along a parabola. The black object experiences Stokes friction.}} |Source=Own work by uploader |Author=[[User:All |
File usage
The following pages on the English Wikipedia use this file (pages on other projects are not listed):
- Ballistics
- Bouncing ball
- Drag (physics)
- Trajectory
- Wave–particle duality
- Talk:Field line
- Talk:Senkaku Islands/Archive 5
- User:Eelaraa/Drag (physics)
- User:Enkyo2/Sandbox-L
- User:Ldm1954/Sandbox/Duality
- Wikipedia:Arbitration/Requests/Clarification and Amendment/Archive 34
- Wikipedia:Requests for arbitration/Tang Dynasty/Workshop
- Wikipedia talk:Requests for arbitration/Tang Dynasty
Global file usage
The following other wikis use this file:
- Usage on af.wikipedia.org
- Usage on ar.wikipedia.org
- Usage on be.wikipedia.org
- Usage on bg.wikipedia.org
- Usage on bn.wikipedia.org
- Usage on bs.wikipedia.org
- Usage on ca.wikipedia.org
- Usage on cv.wikipedia.org
- Usage on da.wikipedia.org
- Usage on de.wikipedia.org
- Usage on el.wikipedia.org
- Usage on eo.wikipedia.org
- Usage on es.wikipedia.org
- Usage on eu.wikipedia.org
- Usage on fa.wikipedia.org
- Usage on fi.wikipedia.org
- Usage on ga.wikipedia.org
- Usage on he.wikipedia.org
- Usage on hi.wikipedia.org
- Usage on hr.wikipedia.org
- Usage on ht.wikipedia.org
- Usage on hu.wikipedia.org
- Usage on hy.wikipedia.org
- Usage on it.wikipedia.org
- Usage on it.wikibooks.org
- Usage on it.wikiversity.org
- Usage on ja.wikipedia.org
- Usage on ja.wikibooks.org
- Usage on kk.wikipedia.org
- Usage on lv.wikipedia.org
- Usage on mk.wikipedia.org
View more global usage of this file.

