Hemi-icosahedron
| Hemi-icosahedron | |
|---|---|
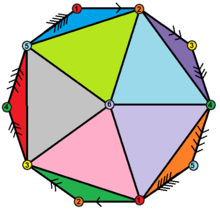 decagonal Schlegel diagram | |
| Type | abstract regular polyhedron globally projective polyhedron |
| Faces | 10 triangles |
| Edges | 15 |
| Vertices | 6 |
| Vertex configuration | 3.3.3.3.3 |
| Schläfli symbol | {3,5}/2 or {3,5}5 |
| Symmetry group | A5, order 60 |
| Dual polyhedron | hemi-dodecahedron |
| Properties | non-orientable Euler characteristic 1 |
A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts.
Geometry
It has 10 triangular faces, 15 edges, and 6 vertices.
It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles.
Graphs
It can be represented symmetrically on faces, and vertices as schlegel diagrams:
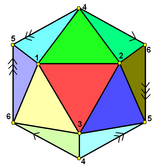
|
| Face-centered |
|---|
The complete graph K6
It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces.
From the point of view of graph theory this is an embedding of (the complete graph with 6 vertices) on a real projective plane. With this embedding, the dual graph is the Petersen graph --- see hemi-dodecahedron.

See also
- 11-cell - an abstract regular 4-polytope constructed from 11 hemi-icosahedra.
- hemi-dodecahedron
- hemi-cube
- hemi-octahedron
References
- McMullen, Peter; Schulte, Egon (December 2002), "6C. Projective Regular Polytopes", Abstract Regular Polytopes (1st ed.), Cambridge University Press, pp. 162–165, ISBN 0-521-81496-0

