Quantum computing

The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.

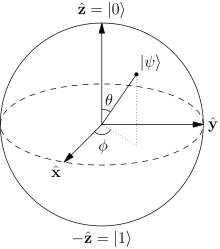
Quantum computing is the study of a non-classical model of computation. Whereas traditional models of computing such as the Turing machine or Lambda calculus rely on "classical" representations of computational memory, a quantum computation could transform the memory into a quantum superposition of possible classical states. A quantum computer is a device that could perform such a computation.

Quantum computing began in the early 1980s, when physicist Paul Benioff proposed a quantum mechanical model of the Turing machine. Richard Feynman and Yuri Manin later suggested that a quantum computer could perform simulations that are out of reach for regular computers. In 1994, Peter Shor developed a polynomial-time quantum algorithm for factoring integers. This was a major breakthrough in the subject: an important method of asymmetric key exchange known as RSA is based on the belief that factoring integers is computationally difficult. The existence of a polynomial-time quantum algorithm proves that one of the most widely used cryptographic protocols is vulnerable to an adversary who possesses a quantum computer. Although it is theoretically accepted that quantum computers could equally be used to counteract against adversarial actions of this kind; with the laws of quantum mechanics applied in this cryptographic capacity (through use of quantum computers) paving the way to quantum cryptography.

Experimental efforts towards building a quantum computer began after a slew of results known as fault-tolerance threshold theorems. These theorems proved that a quantum computation could be efficiently corrected against the effects of large classes of physically realistic noise models. One early result demonstrated parts of Shor's algorithm in a liquid-state nuclear magnetic resonance experiment. Other notable experiments have been performed in superconducting systems, ion-traps, and photonic systems.

Despite rapid and impressive experimental progress, most researchers believe that "fault-tolerant quantum computing [is] still a rather distant dream". On 23 October 2019, Google AI, in partnership with the U.S. National Aeronautics and Space Administration (NASA), officially claimed that its Sycamore quantum processor completed in 200 seconds, a task the equivalent of which would take a state-of-the-art supercomputer approximately 10,000 years to complete. In response, one prominent researcher declared that a quantum computing revolution equivalent to the modern digital computer will require "immense engineering, and probably further insights as well."

There is an increasing amount of investment in quantum computing by governments, established companies, and start-ups. Current research focuses on building and using near-term intermediate-scale devices and demonstrating quantum supremacy. Alongside the long-term goal of building and using a powerful and error-free quantum computer.

The field of quantum computing is closely related to quantum information science, which includes quantum cryptography and quantum communication.

Basic concept

In most models of classical computation, the computer has access to memory. This is a system that can be found in one of a finite set of possible states, each of which is physically distinct. It is frequently convenient to represent the state of this memory as a string of symbols; most simply, as a string of the symbols 0 and 1. In this scenario, the fundamental unit of memory is called a bit and we can measure the "size" of the memory in terms of the number of bits needed to represent fully the state of the memory.

If the memory obeys the laws of quantum physics, the state of the memory could be found in a quantum superposition of different possible "classical" states. If the classical states are to be represented as a string of bits, the quantum memory could be found in any superposition of the possible bit strings. In the quantum scenario, the fundamental unit of memory is called a qubit.

The defining property of a quantum computer is the ability to turn classical memory states into quantum memory states, and vice-versa. This is in contrast to classical computers in that they are designed to only perform computations with memory that never deviates from clearly defined values. To clarify this point, consider that information is normally transmitted through the computer as an electrical signal which can vary between two defined voltage values. If a signal were introduced at a voltage other than those two, the computer's behavior would be undefined.

Of course, in the end we are classical beings and we can only observe classical states. That means the quantum computer must complete its task by returning to us a classical output. To produce these classical outputs, the quantum computer is obliged to measure parts of the memory at various times throughout the computation. The measurement process is inherently probabilistic, meaning that the output of a quantum algorithm is frequently random. The task of a quantum algorithm designer is to ensure that the randomness is tailored to the needs of the problem at hand. For example, if the quantum computer is searching a quantum database for one of several marked items, we can ask the quantum computer to return one of the marked items at random. The quantum computer succeeds in this task as long as it is unlikely to return an unmarked item.

Quantum operations

The prevailing model of quantum computation describes the computation in terms of a network of quantum logic gates. What follows is a brief treatment of the subject based upon Chapter 4 of Nielsen and Chuang.

We may represent the state of a computer memory as a vector whose length is equal to the number of possible states of the memory. So a memory consisting of ${\textstyle n}$bits of information has ${\textstyle 2^{n}}$ possible states, and the vector representing that memory state has ${\textstyle 2^{n}}$ entries. In the classical view, all but one of the entries of this vector would be zero and the remaining entry would be one. The vector should be viewed as a probability vector and represents the fact that the memory is to be found in a particular state with 100% probability (i.e. a probability of one).

In quantum mechanics, probability vectors are generalized to density operators. This is the technically rigorous mathematical foundation for quantum logic gates, but the intermediate quantum state vector formalism is usually introduced first because it is conceptually simpler. Here we focus only on the quantum state vector formalism for simplicity.

We begin by considering a simple memory consisting of only one bit. This memory may be found in one of two states: the zero state or the one state. We may represent the state of this memory using Dirac notation so that

$$|0\rangle :={\begin{pmatrix}1\\0\end{pmatrix}};\quad |1\rangle :={\begin{pmatrix}0\\1\end{pmatrix}}$$

A quantum memory may then be found in any quantum superposition ${\textstyle |\psi \rangle }$ of the two classical states ${\textstyle |0\rangle }$ and ${\textstyle |1\rangle }$:

$$|\psi \rangle :=\alpha \,|0\rangle +\beta \,|1\rangle ={\begin{pmatrix}\alpha \\\beta \end{pmatrix}};\quad |\alpha |^{2}+|\beta |^{2}=1.$$

In general, the coefficients ${\textstyle \alpha }$ and ${\textstyle \beta }$ are complex numbers. In this scenario, we say that one qubit of information can be encoded into the quantum memory. The state ${\textstyle |\psi \rangle }$ is not itself a probability vector but can be connected with a probability vector via a measurement operation. If we choose to measure the quantum memory to determine if the state is ${\textstyle |0\rangle }$ or ${\textstyle |1\rangle }$ (this is known as a computational basis measurement), we would observe the zero state with probability ${\textstyle |\alpha |^{2}}$ and the one state with probability ${\textstyle |\beta |^{2}}$. Please see the article on quantum amplitudes for further information.

To manipulate the state of this one-qubit quantum memory, we imagine applying quantum logic gates analogous to classical logic gates. One obvious gate is the NOT gate, which can be represented by a matrix

$$X:={\begin{pmatrix}0&1\\1&0\end{pmatrix}}.$$

We can formally apply this logic gate to a quantum state vector through matrix multiplication. Thus we find ${\textstyle X|0\rangle =|1\rangle }$ and ${\textstyle X|1\rangle =|0\rangle }$ as expected. But this is not the only interesting single-qubit quantum logic gate. We might, for example, imagine applying one of the other two Pauli matrices.

We may imagine extending single qubit gates to operate on multiqubit quantum memories in two important ways. One way to operate a single qubit gate on a multiqubit memory is simply to select a qubit and apply that gate to the target qubit whilst leaving the remainder of the memory unaffected. Another way is to apply the gate to its target only if another part of the memory is in a desired state. We illustrate this with another example.

Consider a two-qubit quantum memory. Its possible states are

$$|00\rangle :={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}};\quad |01\rangle :={\begin{pmatrix}0\\1\\0\\0\end{pmatrix}};\quad |10\rangle :={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\quad |11\rangle :={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}.$$

We may then define the CNOT gate as the following matrix:

$$CNOT:={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{pmatrix}}.$$

It is easy to check that ${\textstyle CNOT|00\rangle =|00\rangle }$, ${\textstyle CNOT|01\rangle =|01\rangle }$, ${\textstyle CNOT|10\rangle =|11\rangle }$, and ${\textstyle CNOT|11\rangle =|10\rangle }$. In other words, the CNOT applies a NOT gate (${\textstyle X}$ from before) to the second qubit if and only if the first qubit is in the state ${\textstyle |1\rangle }$. If the first qubit is ${\textstyle |0\rangle }$, nothing is done to either qubit.

The preceding discussion is of course a very brief introduction to the concept of a quantum logic gate. Please see the article on quantum logic gates for further information.

To put the story together, we can describe a quantum computation as a network of quantum logic gates and measurements. One can always 'defer' a measurement to the end of a quantum computation, though this can come at a computational cost according to some cost models. Because of this possibility of deferring a measurement, most quantum circuits depict a network consisting only of quantum logic gates and no measurements. For more details on the sequences of operations used for various quantum algorithms, see universal quantum computer, Shor's algorithm, Grover's algorithm, Deutsch–Jozsa algorithm, amplitude amplification, quantum Fourier transform, quantum gate, quantum adiabatic algorithm and quantum error correction.

One can represent any quantum computation as a network of quantum logic gates from a fairly small family of gates. A choice of gate family that enables this construction is known as a universal gate set. One common such set includes all single-qubit gates as well as the CNOT gate from above. This means any quantum computation can be performed by executing a sequence of single-qubit gates together with CNOT gates. Though this gate set is infinite, it can be replaced with a finite gate set by appealing to the Solovay-Kitaev theorem.

Potential

Cryptography

Integer factorization, which underpins the security of public key cryptographic systems, is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes). By comparison, a quantum computer could efficiently solve this problem using Shor's algorithm to find its factors. This ability would allow a quantum computer to break many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm. In particular, the RSA, Diffie–Hellman, and elliptic curve Diffie–Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.

However, other cryptographic algorithms do not appear to be broken by those algorithms. Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory. Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem. It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2^n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2ⁿ in the classical case, meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size).

Quantum cryptography could potentially fulfill some of the functions of public key cryptography. Quantum-based cryptographic systems could, therefore, be more secure than traditional systems against quantum hacking.

Quantum search

Besides factorization and discrete logarithms, quantum algorithms offering a more than polynomial speedup over the best known classical algorithm have been found for several problems, including the simulation of quantum physical processes from chemistry and solid state physics, the approximation of Jones polynomials, and solving Pell's equation. No mathematical proof has been found that shows that an equally fast classical algorithm cannot be discovered, although this is considered unlikely. However, quantum computers offer polynomial speedup for some problems. The most well-known example of this is quantum database search, which can be solved by Grover's algorithm using quadratically fewer queries to the database than that are required by classical algorithms. In this case, the advantage is not only provable but also optimal, it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups. Several other examples of provable quantum speedups for query problems have subsequently been discovered, such as for finding collisions in two-to-one functions and evaluating NAND trees.

Problems that can be addressed with Grover's algorithm have the following properties:

1. There is no searchable structure in the collection of possible answers,
2. The number of possible answers to check is the same as the number of inputs to the algorithm, and
3. There exists a boolean function which evaluates each input and determines whether it is the correct answer

For problems with all these properties, the running time of Grover's algorithm on a quantum computer will scale as the square root of the number of inputs (or elements in the database), as opposed to the linear scaling of classical algorithms. A general class of problems to which Grover's algorithm can be applied is Boolean satisfiability problem. In this instance, the database through which the algorithm is iterating is that of all possible answers. An example (and possible) application of this is a password cracker that attempts to guess the password or secret key for an encrypted file or system. Symmetric ciphers such as Triple DES and AES are particularly vulnerable to this kind of attack. This application of quantum computing is a major interest of government agencies.

Quantum simulation

Since chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, many believe quantum simulation will be one of the most important applications of quantum computing. Quantum simulation could also be used to simulate the behavior of atoms and particles at unusual conditions such as the reactions inside a collider.

Quantum annealing and adiabatic optimization

Quantum annealing or Adiabatic quantum computation relies on the adiabatic theorem to undertake calculations. A system is placed in the ground state for a simple Hamiltonian, which is slowly evolved to a more complicated Hamiltonian whose ground state represents the solution to the problem in question. The adiabatic theorem states that if the evolution is slow enough the system will stay in its ground state at all times through the process.

Solving linear equations

The Quantum algorithm for linear systems of equations or "HHL Algorithm", named after its discoverers Harrow, Hassidim, and Lloyd, is expected to provide speedup over classical counterparts.

Quantum supremacy

John Preskill has introduced the term quantum supremacy to refer to the hypothetical speedup advantage that a quantum computer would have over a classical computer in a certain field. Google announced in 2017 that it expected to achieve quantum supremacy by the end of the year though that did not happen. IBM said in 2018 that the best classical computers will be beaten on some practical task within about five years and views the quantum supremacy test only as a potential future benchmark. Although skeptics like Gil Kalai doubt that quantum supremacy will ever be achieved, Google has been reported to have done so, with calculations more than 3,000,000 times as fast as those of Summit, generally considered the world's fastest computer. Bill Unruh doubted the practicality of quantum computers in a paper published back in 1994. Paul Davies argued that a 400-qubit computer would even come into conflict with the cosmological information bound implied by the holographic principle. In October 2019, a Sycamore processor created in conjunction with Google AI Quantum was reported to have achieved quantum supremacy.

Obstacles

There are a number of technical challenges in building a large-scale quantum computer, and thus far quantum computers have yet to solve a problem faster than a classical computer. David DiVincenzo, of IBM, listed the following requirements for a practical quantum computer:

• scalable physically to increase the number of qubits;
• qubits that can be initialized to arbitrary values;
• quantum gates that are faster than decoherence time;
• universal gate set;
• qubits that can be read easily.

Quantum decoherence

Main article: Quantum decoherence

One of the greatest challenges is controlling or removing quantum decoherence. This usually means isolating the system from its environment as interactions with the external world cause the system to decohere. However, other sources of decoherence also exist. Examples include the quantum gates, and the lattice vibrations and background thermonuclear spin of the physical system used to implement the qubits. Decoherence is irreversible, as it is effectively non-unitary, and is usually something that should be highly controlled, if not avoided. Decoherence times for candidate systems in particular, the transverse relaxation time T₂ (for NMR and MRI technology, also called the dephasing time), typically range between nanoseconds and seconds at low temperature. Currently, some quantum computers require their qubits to be cooled to 20 millikelvins in order to prevent significant decoherence.

As a result, time-consuming tasks may render some quantum algorithms inoperable, as maintaining the state of qubits for a long enough duration will eventually corrupt the superpositions.

These issues are more difficult for optical approaches as the timescales are orders of magnitude shorter and an often-cited approach to overcoming them is optical pulse shaping. Error rates are typically proportional to the ratio of operating time to decoherence time, hence any operation must be completed much more quickly than the decoherence time.

As described in the Quantum threshold theorem, if the error rate is small enough, it is thought to be possible to use quantum error correction to suppress errors and decoherence. This allows the total calculation time to be longer than the decoherence time if the error correction scheme can correct errors faster than decoherence introduces them. An often cited figure for the required error rate in each gate for fault-tolerant computation is 10⁻³, assuming the noise is depolarizing.

Meeting this scalability condition is possible for a wide range of systems. However, the use of error correction brings with it the cost of a greatly increased number of required qubits. The number required to factor integers using Shor's algorithm is still polynomial, and thought to be between L and L², where L is the number of qubits in the number to be factored; error correction algorithms would inflate this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 10⁴ bits without error correction. With error correction, the figure would rise to about 10⁷ bits. Computation time is about L² or about 10⁷ steps and at 1 MHz, about 10 seconds.

A very different approach to the stability-decoherence problem is to create a topological quantum computer with anyons, quasi-particles used as threads and relying on braid theory to form stable logic gates.

Physicist Mikhail Dyakonov has expressed skepticism of quantum computing as follows:

So the number of continuous parameters describing the state of such a useful quantum computer at any given moment must be... about 10³⁰⁰... Could we ever learn to control the more than 10³⁰⁰ continuously variable parameters defining the quantum state of such a system? My answer is simple. No, never.

Developments

Quantum computing models

There are a number of quantum computing models, distinguished by the basic elements in which the computation is decomposed. The four main models of practical importance are:

• Quantum gate array (computation decomposed into a sequence of few-qubit quantum gates)
• One-way quantum computer (computation decomposed into a sequence of one-qubit measurements applied to a highly entangled initial state or cluster state)
• Adiabatic quantum computer, based on quantum annealing (computation decomposed into a slow continuous transformation of an initial Hamiltonian into a final Hamiltonian, whose ground states contain the solution)
• Topological quantum computer (computation decomposed into the braiding of anyons in a 2D lattice)

The quantum Turing machine is theoretically important but the direct implementation of this model is not pursued. All four models of computation have been shown to be equivalent; each can simulate the other with no more than polynomial overhead.

Physical realizations

For physically implementing a quantum computer, many different candidates are being pursued, among them (distinguished by the physical system used to realize the qubits):

• Superconducting quantum computing (qubit implemented by the state of small superconducting circuits (Josephson junctions))
• Trapped ion quantum computer (qubit implemented by the internal state of trapped ions)
• Optical lattices (qubit implemented by internal states of neutral atoms trapped in an optical lattice)
• Quantum dot computer, spin-based (e.g. the Loss-DiVincenzo quantum computer) (qubit given by the spin states of trapped electrons)
• Quantum dot computer, spatial-based (qubit given by electron position in double quantum dot)
• Coupled Quantum Wire (qubit implemented by a pair of Quantum Wires coupled by a Quantum Point Contact)
• Nuclear magnetic resonance quantum computer (NMRQC) implemented with the nuclear magnetic resonance of molecules in solution, where qubits are provided by nuclear spins within the dissolved molecule and probed with radio waves
• Solid-state NMR Kane quantum computers (qubit realized by the nuclear spin state of phosphorus donors in silicon)
• Electrons-on-helium quantum computers (qubit is the electron spin)
• Cavity quantum electrodynamics (CQED) (qubit provided by the internal state of trapped atoms coupled to high-finesse cavities)
• Molecular magnet (qubit given by spin states)
• Fullerene-based ESR quantum computer (qubit based on the electronic spin of atoms or molecules encased in fullerenes)
• Linear optical quantum computer (qubits realized by processing states of different modes of light through linear elements e.g. mirrors, beam splitters and phase shifters)
• Diamond-based quantum computer (qubit realized by the electronic or nuclear spin of nitrogen-vacancy centers in diamond)
• Bose-Einstein condensate-based quantum computer
• Transistor-based quantum computer – string quantum computers with entrainment of positive holes using an electrostatic trap
• Rare-earth-metal-ion-doped inorganic crystal based quantum computers (qubit realized by the internal electronic state of dopants in optical fibers)
• Metallic-like carbon nanospheres based quantum computers

A large number of candidates demonstrates that the topic, in spite of rapid progress, is still in its infancy. There is also a vast amount of flexibility.

Relation to computational complexity theory

Main article: Quantum complexity theory

The suspected relationship of BQP to other problem spaces.

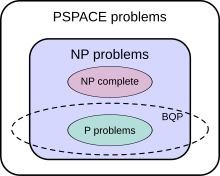
The class of problems that can be efficiently solved by quantum computers is called BQP, for "bounded error, quantum, polynomial time". Quantum computers only run probabilistic algorithms, so BQP on quantum computers is the counterpart of BPP ("bounded error, probabilistic, polynomial time") on classical computers. It is defined as the set of problems solvable with a polynomial-time algorithm, whose probability of error is bounded away from one half. A quantum computer is said to "solve" a problem if, for every instance, its answer will be right with high probability. If that solution runs in polynomial time, then that problem is in BQP.

BQP is contained in the complexity class #P (or more precisely in the associated class of decision problems P^#P), which is a subclass of PSPACE.

BQP is suspected to be disjoint from NP-complete and a strict superset of P, but that is not known. Both integer factorization and discrete log are in BQP. Both of these problems are NP problems suspected to be outside BPP, and hence outside P. Both are suspected to not be NP-complete. There is a common misconception that quantum computers can solve NP-complete problems in polynomial time. That is not known to be true, and is generally suspected to be false.

The capacity of a quantum computer to accelerate classical algorithms has rigid limits—upper bounds of quantum computation's complexity. The overwhelming part of classical calculations cannot be accelerated on a quantum computer. A similar fact prevails for particular computational tasks, like the search problem, for which Grover's algorithm is optimal.

Bohmian Mechanics is a non-local hidden variable interpretation of quantum mechanics. It has been shown that a non-local hidden variable quantum computer could implement a search of an N-item database at most in $O({\sqrt[{3}]{N}})$ steps. This is slightly faster than the $O({\sqrt {N}})$ steps taken by Grover's algorithm. Neither search method will allow quantum computers to solve NP-Complete problems in polynomial time.

Although quantum computers may be faster than classical computers for some problem types, those described above cannot solve any problem that classical computers cannot already solve. A Turing machine can simulate these quantum computers, so such a quantum computer could never solve an undecidable problem like the halting problem. The existence of "standard" quantum computers does not disprove the Church–Turing thesis. It has been speculated that theories of quantum gravity, such as M-theory or loop quantum gravity, may allow even faster computers to be built. Currently, defining computation in such theories is an open problem due to the problem of time, i.e., there currently exists no obvious way to describe what it means for an observer to submit input to a computer and later receive output.

See also

• Supercomputer
• Chemical computer
• D-Wave Systems
• DNA computing
• Electronic quantum holography
• Intelligence Advanced Research Projects Activity
• Kane quantum computer
• List of emerging technologies
• List of quantum processors
• Magic state distillation
• Natural computing
• Normal mode
• Photonic computing
• Post-quantum cryptography
• Quantum annealing
• Quantum bus
• Quantum cognition
• Quantum cryptography
• Quantum gate
• Quantum machine learning
• Quantum threshold theorem
• Rigetti Computing
• Soliton
• Theoretical computer science
• Timeline of quantum computing
• Topological quantum computer
• Valleytronics

Further reading

• Abbot, Derek; Doering, Charles R.; Caves, Carlton M.; Lidar, Daniel M.; Brandt, Howard E.; Hamilton, Alexander R.; Ferry, David K.; Gea-Banacloche, Julio; Bezrukov, Sergey M.; Kish, Laszlo B. (2003). "Dreams versus Reality: Plenary Debate Session on Quantum Computing". Quantum Information Processing. 2 (6): 449–472. arXiv:quant-ph/0310130. doi:10.1023/B:QINP.0000042203.24782.9a. hdl:2027.42/45526.
• Akama, Seiki (2014). Elements of Quantum Computing: History, Theories and Engineering Applications. Springer International Publishing. ISBN 978-3-319-08284-4.
• Ambainis, Andris (1998). "Quantum computation with linear optics". arXiv:quant-ph/9806048.
• Ambainis, Andris (2000). "The Physical Implementation of Quantum Computation". Fortschritte der Physik. 48 (9–11): 771–783. arXiv:quant-ph/0002077. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E.
• Berthiaume, Andre (1997). "Quantum Computation".
• Dibyendu Chatterjee; Arijit Roy (2015). "A transmon-based quantum half-adder scheme". Progress of Theoretical and Experimental Physics. 2015 (9): 093A02(16pages). Bibcode:2015PTEP.2015i3A02C. doi:10.1093/ptep/ptv122.
• Benenti, Giuliano (2004). Principles of Quantum Computation and Information Volume 1. New Jersey: World Scientific. ISBN 978-981-238-830-8. OCLC 179950736.
• DiVincenzo, David P. (1995). "Quantum Computation". Science. 270 (5234): 255–261. Bibcode:1995Sci...270..255D. CiteSeerX 10.1.1.242.2165. doi:10.1126/science.270.5234.255. Table 1 lists switching and dephasing times for various systems.
• Feynman, Richard (1982). "Simulating physics with computers". International Journal of Theoretical Physics. 21 (6–7): 467–488. Bibcode:1982IJTP...21..467F. CiteSeerX 10.1.1.45.9310. doi:10.1007/BF02650179.
• Hiroshi, Imai; Masahito, Hayashi (2006). Quantum Computation and Information. Berlin: Springer. ISBN 978-3-540-33132-2.
• Jaeger, Gregg (2006). Quantum Information: An Overview. Berlin: Springer. ISBN 978-0-387-35725-6. OCLC 255569451.
• Nielsen, Michael; Chuang, Isaac (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 978-0-521-63503-5. OCLC 174527496.
• Keyes, R. W. (1988). "Miniaturization of electronics and its limits". IBM Journal of Research and Development. 32: 84–88. doi:10.1147/rd.321.0024.
• Landauer, Rolf (1961). "Irreversibility and heat generation in the computing process" (PDF).
• Lomonaco, Sam. Four Lectures on Quantum Computing given at Oxford University in July 2006
• Mitchell, Ian (1998). "Computing Power into the 21st Century: Moore's Law and Beyond".
• Moore, Gordon E. (1965). "Cramming more components onto integrated circuits". Electronics Magazine.
• Nielsen, M. A.; Knill, E.; Laflamme, R. "Complete Quantum Teleportation By Nuclear Magnetic Resonance".
• Sanders, Laura (2009). "First programmable quantum computer created".
• Simon, Daniel R. (1994). "On the Power of Quantum Computation". Institute of Electrical and Electronic Engineers Computer Society Press.
• "Simons Conference on New Trends in Quantum Computation". Simons Center for Geometry and Physics, and C. N. Yang Institute for Theoretical Physics. November 15–19, 2010.
• Singer, Stephanie Frank (2005). Linearity, Symmetry, and Prediction in the Hydrogen Atom. New York: Springer. ISBN 978-0-387-24637-6. OCLC 253709076.
• Stolze, Joachim; Suter, Dieter (2004). Quantum Computing. Wiley-VCH. ISBN 978-3-527-40438-4.
• Vandersypen, Lieven M.K.; Yannoni, Constantino S.; Chuang, Isaac L. (2000). Liquid state NMR Quantum Computing.
• Wichert, Andreas (2014). Principles of Quantum Artificial Intelligence. World Scientific Publishing Co. ISBN 978-981-4566-74-2.
• Indian Science News Association, Special Issue of "Science & Culture" on 'A Quantum Jump in Computation', Vol. 85 (5-6), May–June (2019)

External links

• Stanford Encyclopedia of Philosophy: "Quantum Computing" by Amit Hagar and Michael E. Cuffaro.
• Ambainis, Andris (2013). "Quantum Annealing and Computation: A Brief Documentary Note". arXiv:1310.1339 [physics.hist-ph].
• Maryland University Laboratory for Physical Sciences: conducts researches for the quantum computer-based project led by the NSA, named 'Penetrating Hard Target'.
• Visualized history of quantum computing
• "Quantum computation, theory of", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Patenting in the field of quantum computing

Lectures

• Quantum computing for the determined – 22 video lectures by Michael Nielsen
• Video Lectures by David Deutsch
• Lectures at the Institut Henri Poincaré (slides and videos)
• Online lecture on An Introduction to Quantum Computing, Edward Gerjuoy (2008)
• Quantum Computing research by Mikko Möttönen at Aalto University (video) on YouTube