Rule of 72
In finance, the rule of 72, the rule of 70[1] and the rule of 69.3 are methods for estimating an investment's doubling time. The rule number (e.g., 72) is divided by the interest percentage per period (usually years) to obtain the approximate number of periods required for doubling. Although scientific calculators and spreadsheet programs have functions to find the accurate doubling time, the rules are useful for mental calculations and when only a basic calculator is available.[2]
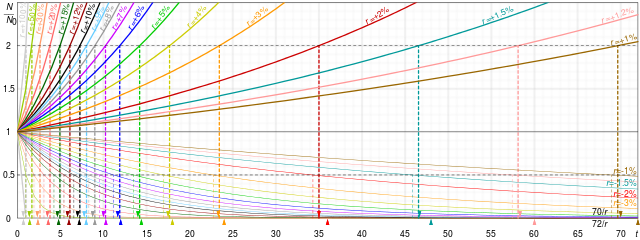
These rules apply to exponential growth and are therefore used for compound interest as opposed to simple interest calculations. They can also be used for decay to obtain a halving time. The choice of number is mostly a matter of preference: 69 is more accurate for continuous compounding, while 72 works well in common interest situations and is more easily divisible. There are a number of variations to the rules that improve accuracy. For periodic compounding, the exact doubling time for an interest rate of r percent per period is
- ,
where t is the number of periods required. The formula above can be used for more than calculating the doubling time. If one wants to know the tripling time, for example, replace the constant 2 in the numerator with 3. As another example, if one wants to know the number of periods it takes for the initial value to rise by 50%, replace the constant 2 with 1.5.
Using the rule to estimate compounding periods[edit]
To estimate the number of periods required to double an original investment, divide the most convenient "rule-quantity" by the expected growth rate, expressed as a percentage.
- For instance, if you were to invest $100 with compounding interest at a rate of 9% per annum, the rule of 72 gives 72/9 = 8 years required for the investment to be worth $200; an exact calculation gives ln(2)/ln(1+0.09) = 8.0432 years.
Similarly, to determine the time it takes for the value of money to halve at a given rate, divide the rule quantity by that rate.
- To determine the time for money's buying power to halve, financiers divide the rule-quantity by the inflation rate. Thus at 3.5% inflation using the rule of 70, it should take approximately 70/3.5 = 20 years for the value of a unit of currency to halve.[1]
- To estimate the impact of additional fees on financial policies (e.g., mutual fund fees and expenses, loading and expense charges on variable universal life insurance investment portfolios), divide 72 by the fee. For example, if the Universal Life policy charges an annual 3% fee over and above the cost of the underlying investment fund, then the total account value will be cut to 50% in 72 / 3 = 24 years, and then to 25% of the value in 48 years, compared to holding exactly the same investment outside the policy.
Choice of rule[edit]
The value 72 is a convenient choice of numerator, since it has many small divisors: 1, 2, 3, 4, 6, 8, 9, and 12. It provides a good approximation for annual compounding, and for compounding at typical rates (from 6% to 10%); the approximations are less accurate at higher interest rates.
For continuous compounding, 69 gives accurate results for any rate, since ln(2) is about 69.3%; see derivation below. Since daily compounding is close enough to continuous compounding, for most purposes 69, 69.3 or 70 are better than 72 for daily compounding. For lower annual rates than those above, 69.3 would also be more accurate than 72.[3] For higher annual rates, 78 is more accurate.
| Rate | Actual Years | Rate × Actual Years | Rule of 72 | Rule of 70 | Rule of 69.3 | 72 adjusted | E-M rule |
|---|---|---|---|---|---|---|---|
| 0.25% | 277.605 | 69.401 | 288.000 | 280.000 | 277.200 | 277.667 | 277.547 |
| 0.5% | 138.976 | 69.488 | 144.000 | 140.000 | 138.600 | 139.000 | 138.947 |
| 1% | 69.661 | 69.661 | 72.000 | 70.000 | 69.300 | 69.667 | 69.648 |
| 2% | 35.003 | 70.006 | 36.000 | 35.000 | 34.650 | 35.000 | 35.000 |
| 3% | 23.450 | 70.349 | 24.000 | 23.333 | 23.100 | 23.444 | 23.452 |
| 4% | 17.673 | 70.692 | 18.000 | 17.500 | 17.325 | 17.667 | 17.679 |
| 5% | 14.207 | 71.033 | 14.400 | 14.000 | 13.860 | 14.200 | 14.215 |
| 6% | 11.896 | 71.374 | 12.000 | 11.667 | 11.550 | 11.889 | 11.907 |
| 7% | 10.245 | 71.713 | 10.286 | 10.000 | 9.900 | 10.238 | 10.259 |
| 8% | 9.006 | 72.052 | 9.000 | 8.750 | 8.663 | 9.000 | 9.023 |
| 9% | 8.043 | 72.389 | 8.000 | 7.778 | 7.700 | 8.037 | 8.062 |
| 10% | 7.273 | 72.725 | 7.200 | 7.000 | 6.930 | 7.267 | 7.295 |
| 11% | 6.642 | 73.061 | 6.545 | 6.364 | 6.300 | 6.636 | 6.667 |
| 12% | 6.116 | 73.395 | 6.000 | 5.833 | 5.775 | 6.111 | 6.144 |
| 15% | 4.959 | 74.392 | 4.800 | 4.667 | 4.620 | 4.956 | 4.995 |
| 18% | 4.188 | 75.381 | 4.000 | 3.889 | 3.850 | 4.185 | 4.231 |
| 20% | 3.802 | 76.036 | 3.600 | 3.500 | 3.465 | 3.800 | 3.850 |
| 25% | 3.106 | 77.657 | 2.880 | 2.800 | 2.772 | 3.107 | 3.168 |
| 30% | 2.642 | 79.258 | 2.400 | 2.333 | 2.310 | 2.644 | 2.718 |
| 40% | 2.060 | 82.402 | 1.800 | 1.750 | 1.733 | 2.067 | 2.166 |
| 50% | 1.710 | 85.476 | 1.440 | 1.400 | 1.386 | 1.720 | 1.848 |
| 60% | 1.475 | 88.486 | 1.200 | 1.167 | 1.155 | 1.489 | 1.650 |
| 70% | 1.306 | 91.439 | 1.029 | 1.000 | 0.990 | 1.324 | 1.523 |
Note: The most accurate value on each row is in italics, and the most accurate of the simpler rules in bold.
History[edit]
An early reference to the rule is in the Summa de arithmetica (Venice, 1494. Fol. 181, n. 44) of Luca Pacioli (1445–1514). He presents the rule in a discussion regarding the estimation of the doubling time of an investment, but does not derive or explain the rule, and it is thus assumed that the rule predates Pacioli by some time.
A voler sapere ogni quantità a tanto per 100 l'anno, in quanti anni sarà tornata doppia tra utile e capitale, tieni per regola 72, a mente, il quale sempre partirai per l'interesse, e quello che ne viene, in tanti anni sarà raddoppiato. Esempio: Quando l'interesse è a 6 per 100 l'anno, dico che si parta 72 per 6; ne vien 12, e in 12 anni sarà raddoppiato il capitale. (emphasis added).
Roughly translated:
In wanting to know of any capital, at a given yearly percentage, in how many years it will double adding the interest to the capital, keep as a rule [the number] 72 in mind, which you will always divide by the interest, and what results, in that many years it will be doubled. Example: When the interest is 6 percent per year, I say that one divides 72 by 6; 12 results, and in 12 years the capital will be doubled.
Adjustments for higher accuracy[edit]
For higher rates, a larger numerator would be better (e.g., for 20%, using 76 to get 3.8 years would be only about 0.002 off, where using 72 to get 3.6 would be about 0.2 off). This is because, as above, the rule of 72 is only an approximation that is accurate for interest rates from 6% to 10%.
For every three percentage points away from 8%, the value of 72 could be adjusted by 1:
or, for the same result:
Both of these equations simplify to:
Note that is quite close to 69.3.
E-M rule[edit]
The Eckart–McHale second-order rule (the E-M rule) provides a multiplicative correction for the rule of 69.3 that is very accurate for rates from 0% to 20%, whereas the rule is normally only accurate at the lowest end of interest rates, from 0% to about 5%.
To compute the E-M approximation, multiply the rule of 69.3 result by 200/(200−r) as follows:
- .
For example, if the interest rate is 18%, the rule of 69.3 gives t = 3.85 years, which the E-M rule multiplies by (i.e. 200/ (200−18)) to give a doubling time of 4.23 years. As the actual doubling time at this rate is 4.19 years, the E-M rule thus gives a closer approximation than the rule of 72.
To obtain a similar correction for the rule of 70 or 72, one of the numerators can be set and the other adjusted to keep their product approximately the same. The E-M rule could thus be written also as
- or
In these variants, the multiplicative correction becomes 1 respectively for r=2 and r=8, the values for which the rules of 70 and 72 are most accurate.
Padé approximant[edit]
The third-order Padé approximant gives a more accurate answer over an even larger range of r, but it has a slightly more complicated formula:
which simplifies to:
Derivation[edit]
Periodic compounding[edit]
For periodic compounding, future value is given by:
where is the present value, is the number of time periods, and stands for the interest rate per time period.
The future value is double the present value when:
which is the following condition:
This equation is easily solved for :
A simple rearrangement shows:
If r is small, then ln(1 + r) approximately equals r (this is the first term in the Taylor series). That is, the latter factor grows slowly when is close to zero.
Call this latter factor . The function is shown to be accurate in the approximation of for a small, positive interest rate when (see derivation below). , and we therefore approximate time as:
Written as a percentage:
This approximation increases in accuracy as the compounding of interest becomes continuous (see derivation below). is written as a percentage.
In order to derive the more precise adjustments presented above, it is noted that is more closely approximated by (using the second term in the Taylor series). can then be further simplified by Taylor approximations:
Replacing the "R" in R/200 on the third line with 7.79 gives 72 on the numerator. This shows that the rule of 72 is most accurate for periodically compounded interests around 8%. Similarly, replacing the "R" in R/200 on the third line with 2.02 gives 70 on the numerator, showing the rule of 70 is most accurate for periodically compounded interests around 2%.
Alternatively, the E-M rule is obtained if the second-order Taylor approximation is used directly.
Continuous compounding[edit]
For continuous compounding, the derivation is simpler and yields a more accurate rule:
See also[edit]
References[edit]
- ^ a b Donella Meadows, Thinking in Systems: A Primer, Chelsea Green Publishing, 2008, page 33 (box "Hint on reinforcing feedback loops and doubling time").
- ^ Slavin, Steve (1989). All the Math You'll Ever Need. John Wiley & Sons. pp. 153–154. ISBN 0-471-50636-2.
- ^ Kalid Azad Demystifying the Natural Logarithm (ln) from BetterExplained
External links[edit]
- The Scales Of 70 – extends the rule of 72 beyond fixed-rate growth to variable rate compound growth including positive and negative rates.