Talk:Symmetric graph

Definitions[edit]

I have reworded the article to agree with the definition in the cited references. Radagast3 (talk) 08:38, 26 March 2009 (UTC)[reply]

The wording "a graph is symmetric if its automorphism group acts transitively upon ... edges considered as having a direction" covers the fact that in Wikipedia directed edge currently refers to an edge in a directed graph, and other words are needed. Radagast3 (talk) 09:50, 27 March 2009 (UTC)[reply]

Arc-transitive graph currently redirects here, since the major texts use the words as synonyms. Radagast3 (talk) 09:54, 27 March 2009 (UTC)[reply]

I have added a clarifying para regarding the confusion over the term "symmetric." I think following Biggs (symmetric = arc-transitive) is the best course of action here (as we have done during the expansion of related articles since March), since arc-transitivity is the more important concept. I note that the MathWorld definition is a complete dog's breakfast, trying to equate two different definitions, and then giving an example where they differ. — Radagast3 (talk) 03:32, 4 September 2009 (UTC)[reply]

That material was already present two paragraphs up. I merged your new paragraph with the old one. Apparently vertex-transitive + edge-transitive is also called (less ambiguously) half-transitive. —David Eppstein (talk) 03:39, 4 September 2009 (UTC)[reply]

Thanks! Goes to show the danger of poorly-thought-out edits. I even wrote the material two paragraphs up. — Radagast3 (talk) 03:59, 4 September 2009 (UTC)[reply]

The main fact is that everybody is interested in cubic symmetric graphs. And for cubic graphs there is an equivalence beetween "vertex-transitive + edge-transitive" and "arc-transitive". In fac a half-transitive graph which is not symmetric need to be of even degree. Koko90 (talk) 07:24, 4 September 2009 (UTC)[reply]

Yes, as you say, the equivalence for cubic graphs makes the difference between "vertex-transitive + edge-transitive" and "arc-transitive" unimportant for the cubic case. However, it is important that the collection of definitions in Wikipedia be consistent, and there are some other important properties about arc-transitive graphs. — Radagast3 (talk) 08:08, 4 September 2009 (UTC)[reply]

I agree, definitions in Wikipedia need to be consistent.Koko90 (talk) 08:55, 4 September 2009 (UTC)[reply]

Similarly, this article makes two references to "linked" vertices. Unless this is a concept I haven't come across, this should be replaced by the more common term "adjacent". Or if u and v linked means there exists a u-v path, then we need to talk about u and v being in the same connected component or something like this. Triangl (talk) 18:47, 6 January 2011 (UTC)[reply]

A "half-transitive" article?[edit]

I'm wondering if we should have an article on half-transitive graphs. It would literally say only:

A half-transitive graph is one that is vertex-transitive and edge-transitive. Every connected symmetric graph must be half-transitive, and half-transitive graphs of odd degree are always symmetric, but there exist graphs that are half-transitive yet not symmetric. The smallest half-transitive but not symmetric graph is Holt's graph, with degree 4 and 27 vertices.

If yes, we should probably update the template, and create a picture of Holt's graph to use as an illustration. If no, we should probably change the red link in this article to a bold. I'm currently leaning towards "no," since there's just not enough to say about half-transitive graphs. — Radagast3 (talk) 00:37, 5 September 2009 (UTC)[reply]

Google scholar finds 29 articles on half-transitive graphs. That seems like enough to say more than that short paragraph about them. —David Eppstein (talk) 00:38, 5 September 2009 (UTC)[reply]

Possibly, although much of that material might not be at the right level for Wikipedia. A revised template would look like this, I think:

— Radagast3 (talk) 00:49, 5 September 2009 (UTC)[reply]

Yes, we need a "half-transitive" article. By the way, i will write an article about the Holt's graph and draw a few illustration as soon as possible. PS : for the templaye you can add semi-symmetric (with only one arrow, semi-symmetric -> edge-transitive and regular). Koko90 (talk) 07:50, 5 September 2009 (UTC)[reply]

I have updated the template, and created the half-transitive graph article, since we have two strong votes for it. I will be very grateful, Koko90, if you will handle Holt's graph.

The "edge-transitive and regular" entry in the table actually clicks to "semi-symmetric".

— Radagast3 (talk) 08:54, 5 September 2009 (UTC)[reply]

The problem with "semi-symmetric" is that a "edge-transitive and regular" graph is not "semi-symmetric" if it is symmetric. A semi-symmetric graph, by definition, can't be symmetric. It is a edge-transitive and regular graph that is not vertex transitive. Koko90 (talk) 09:23, 5 September 2009 (UTC)[reply]

I understand exactly what you mean, and the same thing has now happened with half-transitive: the table entry is not quite the same as the article pointed to. I'm not sure how to resolve this (there's a limit to how much we can squeeze into the table), so I'm tempted to leave things as they are until inspiration strikes. — Radagast3 (talk) 09:47, 5 September 2009 (UTC)[reply]

The "edge-transitive and regular" / "semi-symmetric" entry in the table is David's by the way, so he might be able to further explain it, but it seems a reasonable response to conflicting issues (the definition of a class that's "A" but not "B", and the limited space in the table). — Radagast3 (talk) 09:51, 5 September 2009 (UTC)[reply]

Actually, I've had to make a few changes: checking the reference I see we got the definition wrong. — Radagast3 (talk) 09:19, 5 September 2009 (UTC)[reply]

The article on Holt's graph should probably be Holt graph for consistency... I'll start a stub. — Radagast3 (talk) 13:23, 6 September 2009 (UTC)[reply]

Table of examples[edit]

The table {{Graph families defined by their automorphisms}} is excellent. I was wondering if we could have a larger version of the same table somewhere, with an illustration for each of the families? (Just one "representative" example of a graph per family.) Or do we already have something like? I am not sure where it would belong, perhaps somewhere near Graph automorphism#Graph families defined by their automorphisms? — Miym (talk) 11:02, 5 September 2009 (UTC)[reply]

It's a good idea. It's not entirely obvious which examples to use... they would need to be fairly small in order to fit, but would also have to be chosen to be a member only of the selected table entry. Possibilities include:

1. Distance-transitive graph: want an example which is not strongly regular, so not the Petersen graph.

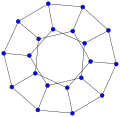
2. Symmetric graph: perhaps the Möbius–Kantor graph, which is not distance-transitive.

3. Vertex- and edge-transitive: perhaps Holt's graph, which is half-transitive, i.e. not symmetric.

4. Edge-transitive and regular: perhaps the Folkman graph or the Gray graph, which are semi-symmetric.

5. Edge-transitive graph: perhaps K_2,3 or similar, which is not regular.

6. Vertex-transitive graph: want an example which is not edge-transitive and not a Cayley graph.

7. Regular graph: perhaps the Frucht graph, which is not vertex-transitive.

8. Cayley graph: perhaps the one on the right.

9. Strongly regular graph: want an example which is not distance-transitive,

10. Distance-regular graph: want an example which is not distance-transitive or strongly regular.

— Radagast3 (talk) 11:42, 5 September 2009 (UTC)[reply]

Perhaps something like this (as yet incomplete and with formatting problems):

(the table that was here has been moved to Graph automorphism#Graph families defined by their automorphisms, even though it is still incomplete).

— Radagast3 (talk) 23:10, 5 September 2009 (UTC)[reply]

Updated table. — Radagast3 (talk) 04:14, 6 September 2009 (UTC)[reply]

Moved table to Graph automorphism#Graph families defined by their automorphisms. It still needs images for:

a. Distance-regular graph: ideally, want an example which is not distance-transitive or strongly regular.

b. Vertex- and edge-transitive: perhaps Holt's graph, which is half-transitive, i.e. not symmetric.

c. Vertex-transitive graph: ideally, want an example which is not edge-transitive and not a Cayley graph.

— Radagast3 (talk) 05:21, 6 September 2009 (UTC)[reply]

Many thanks, looks great! I was wondering if we should also add some figure captions, like in the example below?

It might avoid some confusion (we are not showing "the regular graph" but just the Frucht graph which is a regular graph).
For an interested reader, we would have links to pages which explain the illustration (and, hopefully at least in future, also explain why the particular graph is classified the way it is).

(Or does it look too messy? Another possibility might be to have footnotes with similar links and further explanations.) A related comment: it might be a good idea if, e.g., Edge-transitive graph had an illustration of the same example K_3,2 as what we have in the table; then a reader who clicks on Edge-transitive graph instead of K_3,2 would also see a familiar-looking example, and the figure caption on that page would provide more details, e.g., explaining that the graph is edge-transitive and not regular. — Miym (talk) 11:50, 6 September 2009 (UTC)[reply]

Dodecahedron	Shrikhande graph	Paley graph
distance-transitive	distance-regular	strongly regular

F26A graph	Nauru graph
symmetric (arc-transitive)	t-transitive, t ≥ 2
(if connected)
	Folkman graph	K_3,2
vertex- and edge-transitive	edge-transitive and regular	edge-transitive

Truncated tetrahedron	Frucht graph
vertex-transitive	regular

Cayley graph for Z₂ × Z₃
Cayley graph

Hmmm. I like the idea in principle, but it does seem to make the table too cluttered. I've tried something more subtle instead. Possibly too subtle.

As to changing the pointed-to articles to match... it's worth thinking about, but I'm sure the images already in those articles are well-chosen.

– Radagast3 (talk) 12:14, 6 September 2009 (UTC)[reply]

The current version looks like a good compromise to me. It just bothers me a bit that the tooltips of the figures are "#" which isn't that informative. Here is an attempt to create a simple version with little clutter and with useful tooltips. Here each image has a tooltip that contains the name of the graph, and each image is a link to the relevant article about the graph. (Note that in this version the tooltips don't have to match the names of the target pages – e.g., "Skeleton of the dodecahedron" vs. "Dodecahedron" – so it's possible to include some extra information in the tooltips for the benefit of those who happen to notice them.) — Miym (talk) 13:00, 6 September 2009 (UTC)[reply]

Skeleton of the dodecahedron	Shrikhande graph	Paley graph
distance-transitive	distance-regular	strongly regular

F26A graph	Nauru graph
symmetric (arc-transitive)	t-transitive, t ≥ 2
(if connected)
Holt's graph	Folkman graph	Complete bipartite graph K3,2
vertex- and edge-transitive	edge-transitive and regular	edge-transitive

Skeleton of the truncated tetrahedron	Frucht graph
vertex-transitive	regular

Skeleton of the triangular prism
Cayley graph

Looks great! – Radagast3 (talk) 13:12, 6 September 2009 (UTC)[reply]

I observe that the graph appearing (twice) above and described as a "Cayley graph" is not a Cayley graph. Cayley graphs are directed. This does not matter much for the red edges (there's a convention that an undirected edge connected to no other edge of the same color means a two-cycle of that color). But depending on the direction of the black edges, it might by a Cayley graph for Z₂ × Z₃, or for the dihedral group of order 6. Maproom (talk) 07:04, 5 May 2015 (UTC)[reply]

Case of the oriented graphs[edit]

Hello,

This article apparently applies to unoriented graphs. But, as the German page states it,

"Als symmetrischen Graph bezeichnet man in der Graphentheorie einen gerichteten Graphen, bei dem zwischen zwei seiner Knoten jeweils entweder keine (gerichtete) Kante verläuft oder aber Kanten in beide Richtungen verlaufen."

a "symmetric graph" can also be an oriented graph where two vertices are either unconnected or connected in both directions.

This definition of a symmetric graph boils down to the definition of an unoriented graph, but it is nevertheless used in the math literature. It's also the definition that appears on French wiktionnary. --MathsPoetry (talk) 21:23, 20 April 2012 (UTC)[reply]

Terminology[edit]

This article uses the terms "2-transitive", "3-transitive", etc., in a way incompatible with most (maybe all) other sources. In other sources, such as the Mathieu group article, n-transitive is used, as defined here, in relation to sets of n points, and so is stronger than when used as in this article in relation to arcs of n points. Sources such as this use the term "n-arc-transitive" for transitivity in relation to arcs of n points.

I plan to edit all occurrences of "n-transitive" in the article to "n-arc-transitive", unless someone can explain why I shouldn't, citing sources that use the term as used here. Maproom (talk) 06:54, 5 May 2015 (UTC)[reply]

Requested move 8 April 2018[edit]

The following is a closed discussion of a requested move. Please do not modify it. Subsequent comments should be made in a new section on the talk page. Editors desiring to contest the closing decision should consider a move review. No further edits should be made to this section.

The result of the move request was: consensus not to move the page as proposed at this time, per the discussion below. Thanks to all for their participation in the discussion. Dekimasuよ! 01:42, 20 April 2018 (UTC)[reply]

Symmetric graph → Arc-transitive graph – This type of graph is usually called an arc-transitive graph. A symmetric graph can also be a graph that is both vertex-transitive and edge-transitive. The article also mentions t-arc-transitive graphs, which are never called t-symmetric graphs. Therefore, this page should be moved to arc-transitive graph. Math Maniac (talk) 15:32, 8 April 2018 (UTC)--Relisting. Dekimasuよ! 18:21, 15 April 2018 (UTC)[reply]

Oppose. Search on Scholar Google provides 768 hits for "arc-transitive graph", and 4420 hits for "symmetric graph". This does not prove that the name arc-transitive graph is less usual, but this proves that better sources are needed for asserting that symmetric graph is not the usual name. Moreover, the symmetry of a symmetric graph is more "richer" than being simply arc-transitive. In fact, the article say: "Every connected symmetric graph must thus be both vertex-transitive and edge-transitive, and the converse is true for graphs of odd degree". Thus the symmetry is not reduced to arc-transitivity, and applies also on vertices. Finally, the article is about non-oriented graphs, and the use of "arc" (usually referring to oriented graphs) in the title would be misleading. D.Lazard (talk) 13:10, 18 April 2018 (UTC)[reply]

Oppose per the good points raised by D. Lazard. --Mark viking (talk) 17:52, 18 April 2018 (UTC)[reply]
Oppose. The term "arc-transitive" more properly refers to a weaker symmetry condition on directed graphs (e.g. see Conder, Lorimer, and Praeger, "Constructions for arc-transitive digraphs"): a directed graph in which every directed edge is symmetric to every other directed edge. Its application to symmetric graphs reflects a specific point of view of directed graphs: that they are the same thing as undirected graphs in which each arc has an opposite arc between the same two vertices. The "symmetric graph" terminology is therefore less ambiguous (because it cannot be used for directed graphs that do not have opposite arcs) and less specific to the graph=special class of digraphs point of view, as well as (per D. Lazard) being more commonly used. —David Eppstein (talk) 18:09, 18 April 2018 (UTC)[reply]
Strong oppose. As pointed out above, the terms have different meanings, see e.g. Holt graph for an example of a graph which is arc-transitive (and vertex-transitive) but not symmetric. Maproom (talk) 19:16, 18 April 2018 (UTC)[reply]

The above discussion is preserved as an archive of a requested move. Please do not modify it. Subsequent comments should be made in a new section on this talk page or in a move review. No further edits should be made to this section.

I know that this discussion is finished, but I would like to point out that Maproom was wrong. The Holt graph is not arc-transitive by any definition. It is a graph that is vertex-transitive and edge-transitive, but not arc-transitive. By a common definition of symmetric graph, the Holt graph is symmetric. The fact that symmetric graph and arc-transitive graph have different meanings is the reason that this page should be moved. Math Maniac (talk) 19:08, 28 July 2018 (UTC)[reply]

Math Maniac is right. When I !voted above, I was unaware that "arc-transitive" standardly means "directed-arc transitive". Maproom (talk) 10:19, 30 July 2018 (UTC)[reply]

Question about defintion[edit]

I just read the definition of a symmetric graph in the book Topics in Algebraic Graph Theory (Beineke and Wilson, eds., 2007).

That definition differs from the one in this article, because the book's definition requires not only that the automorphism group of a graph be transitive on edges, but also that it be transitive on vertices.

Are both definitions used currently by researchers? If so, the article should mention this fact.

Or is one of these definitions wrong?

Of course, for a graph G, IF for any two distinct vertices v and w ∊ G, both of [v,w] and [w,v] are always considered to be edges of G ... then transitivity on vertices would follow from transitivity on edges. 2601:200:C000:1A0:F8A4:C598:11E7:9879 (talk) 17:56, 21 June 2022 (UTC)[reply]

A definition cannot be wrong, as it results from a choice. The second paragraph of the lead says that the two definitions are equivalent if there is no isolated vertex. Also, trivially, a symmetric graph for the definition of the article remains symmetric if one adds or removes isolated vertices. Thus, in practice, nobody consider symmetric graphs with isolated vertices, and the choice between the definitions does not really matter. D.Lazard (talk) 18:18, 21 June 2022 (UTC)[reply]

So if in Wikipedia I defined the number 2 as 1 + 1 + 1, you would not consider that wrong?

You seem to have concluded that the only way for a graph G=(V,E) [to have its automorphism group Aut(G) be transitive on edges but not on vertices] is when there are isolated vertices? Is that right? 2601:200:C000:1A0:9D6A:3426:156B:13FB (talk) 03:29, 22 June 2022 (UTC)[reply]

Please, read the article: "By definition, a symmetric graph without isolated vertices must also be vertex-transitive" and "However, an edge-transitive graph need not be symmetric" mean that your assertion is wrong, but becomes true if you replace "edge" by "ordered pair of adjacent vertices". D.Lazard (talk) 07:01, 22 June 2022 (UTC)[reply]

Since I don't yet know how much I can rely on the article, I am not presuming that everything therein is corrrect. 2601:200:C000:1A0:D0B:17BA:E5BF:AD9F (talk) 19:47, 22 June 2022 (UTC)[reply]