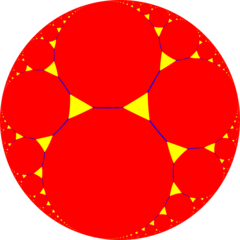
Hexagonal tiling honeycomb
| Hexagonal tiling honeycomb | |
|---|---|
 Perspective projection view within Poincaré disk model | |
| Type | Hyperbolic regular honeycomb Paracompact uniform honeycomb |
| Schläfli symbols | {6,3,3} t{3,6,3} 2t{6,3,6} 2t{6,3[3]} t{3[3,3]} |
| Coxeter diagrams | |
| Cells | {6,3} |
| Faces | hexagon {6} |
| Edge figure | triangle {3} |
| Vertex figure |  tetrahedron {3,3} |
| Dual | Order-6 tetrahedral honeycomb |
| Coxeter groups | , [3,3,6] , [3,6,3] , [6,3,6] , [6,3[3]] , [3[3,3]] |
| Properties | Regular |
In the field of hyperbolic geometry, the hexagonal tiling honeycomb is one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is paracompact because it has cells composed of an infinite number of faces. Each cell is a hexagonal tiling whose vertices lie on a horosphere, a surface in hyperbolic space that approaches a single ideal point at infinity.
The Schläfli symbol of the hexagonal tiling honeycomb is {6,3,3}. Since that of the hexagonal tiling is {6,3}, this honeycomb has three such hexagonal tilings meeting at each edge. Since the Schläfli symbol of the tetrahedron is {3,3}, the vertex figure of this honeycomb is a tetrahedron. Thus, four hexagonal tilings meet at each vertex of this honeycomb, six hexagons meet at each vertex, and four edges meet at each vertex.[1]
Images[edit]
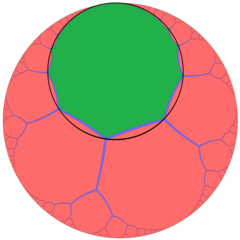
Viewed in perspective outside of a Poincaré disk model, the image above shows one hexagonal tiling cell within the honeycomb, and its mid-radius horosphere (the horosphere incident with edge midpoints). In this projection, the hexagons grow infinitely small towards the infinite boundary, asymptoting towards a single ideal point. It can be seen as similar to the order-3 apeirogonal tiling, {∞,3} of H2, with horocycles circumscribing vertices of apeirogonal faces.
| {6,3,3} | {∞,3} |
|---|---|

|
|
| One hexagonal tiling cell of the hexagonal tiling honeycomb | An order-3 apeirogonal tiling with a green apeirogon and its horocycle |
Symmetry constructions[edit]
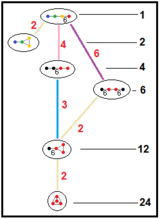
It has a total of five reflectional constructions from five related Coxeter groups all with four mirrors and only the first being regular: ![]()
![]()
![]()
![]()
![]()
![]()
![]() [6,3,3],
[6,3,3], ![]()
![]()
![]()
![]()
![]()
![]()
![]() [3,6,3],
[3,6,3], ![]()
![]()
![]()
![]()
![]()
![]()
![]() [6,3,6],
[6,3,6], ![]()
![]()
![]()
![]()
![]() [6,3[3]] and [3[3,3]]
[6,3[3]] and [3[3,3]] ![]()
![]()
![]() , having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)*] (remove 3 mirrors, index 24 subgroup); [3,6,3*] or [3*,6,3] (remove 2 mirrors, index 6 subgroup); [1+,6,3,6,1+] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3[3,3]]. The ringed Coxeter diagrams are
, having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)*] (remove 3 mirrors, index 24 subgroup); [3,6,3*] or [3*,6,3] (remove 2 mirrors, index 6 subgroup); [1+,6,3,6,1+] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3[3,3]]. The ringed Coxeter diagrams are ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() and
and ![]()
![]()
![]() , representing different types (colors) of hexagonal tilings in the Wythoff construction.
, representing different types (colors) of hexagonal tilings in the Wythoff construction.
Related polytopes and honeycombs[edit]
The hexagonal tiling honeycomb is a regular hyperbolic honeycomb in 3-space, and one of 11 which are paracompact.
| 11 paracompact regular honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 {6,3,3} |
 {6,3,4} |
 {6,3,5} |
 {6,3,6} |
 {4,4,3} |
 {4,4,4} | ||||||
 {3,3,6} |
 {4,3,6} |
 {5,3,6} |
 {3,6,3} |
 {3,4,4} | |||||||
It is one of 15 uniform paracompact honeycombs in the [6,3,3] Coxeter group, along with its dual, the order-6 tetrahedral honeycomb.
| [6,3,3] family honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {6,3,3} | r{6,3,3} | t{6,3,3} | rr{6,3,3} | t0,3{6,3,3} | tr{6,3,3} | t0,1,3{6,3,3} | t0,1,2,3{6,3,3} | ||||

|

|

|

|

|

|

|

| ||||

|

|

|

|

|

|

| |||||
| {3,3,6} | r{3,3,6} | t{3,3,6} | rr{3,3,6} | 2t{3,3,6} | tr{3,3,6} | t0,1,3{3,3,6} | t0,1,2,3{3,3,6} | ||||
It is part of a sequence of regular polychora, which include the 5-cell {3,3,3}, tesseract {4,3,3}, and 120-cell {5,3,3} of Euclidean 4-space, along with other hyperbolic honeycombs containing tetrahedral vertex figures.
| {p,3,3} honeycombs | ||||||||
|---|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | ||||||
| Form | Finite | Paracompact | Noncompact | |||||
| Name | {3,3,3} | {4,3,3} | {5,3,3} | {6,3,3} | {7,3,3} | {8,3,3} | ... {∞,3,3} | |
| Image | 
|

|

|

|

|
|

| |
Coxeter diagrams
|
1 | |||||||
| 4 | ||||||||
| 6 | ||||||||
| 12 | ||||||||
| 24 | ||||||||
| Cells {p,3} |
 {3,3} |
 {4,3} |
 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
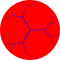 {∞,3} | |
It is also part of a sequence of regular honeycombs of the form {6,3,p}, which are each composed of hexagonal tiling cells:
| {6,3,p} honeycombs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | H3 | ||||||||||
| Form | Paracompact | Noncompact | |||||||||
| Name | {6,3,3} | {6,3,4} | {6,3,5} | {6,3,6} | {6,3,7} | {6,3,8} | ... {6,3,∞} | ||||
| Coxeter |
|||||||||||
| Image | 
|

|

|

|

|

|

| ||||
| Vertex figure {3,p} |
{3,3} |
{3,4} |
{3,5} |
{3,6} |
{3,7} |
{3,8} |
{3,∞} | ||||
Rectified hexagonal tiling honeycomb[edit]
| Rectified hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | r{6,3,3} or t1{6,3,3} |
| Coxeter diagrams | |
| Cells | {3,3} r{6,3} |
| Faces | triangle {3} hexagon {6} |
| Vertex figure | 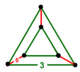 triangular prism |
| Coxeter groups | , [3,3,6] , [3,3[3]] |
| Properties | Vertex-transitive, edge-transitive |
The rectified hexagonal tiling honeycomb, t1{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has tetrahedral and trihexagonal tiling facets, with a triangular prism vertex figure. The
has tetrahedral and trihexagonal tiling facets, with a triangular prism vertex figure. The ![]()
![]()
![]()
![]()
![]() half-symmetry construction alternates two types of tetrahedra.
half-symmetry construction alternates two types of tetrahedra.
| Hexagonal tiling honeycomb |
Rectified hexagonal tiling honeycomb |
|---|---|

|

|
| Related H2 tilings | |
| Order-3 apeirogonal tiling |
Triapeirogonal tiling |
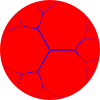
|
 
|
Truncated hexagonal tiling honeycomb[edit]
| Truncated hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t{6,3,3} or t0,1{6,3,3} |
| Coxeter diagram | |
| Cells | {3,3} t{6,3} |
| Faces | triangle {3} dodecagon {12} |
| Vertex figure |  triangular pyramid |
| Coxeter groups | , [3,3,6] |
| Properties | Vertex-transitive |
The truncated hexagonal tiling honeycomb, t0,1{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has tetrahedral and truncated hexagonal tiling facets, with a triangular pyramid vertex figure.
has tetrahedral and truncated hexagonal tiling facets, with a triangular pyramid vertex figure.
It is similar to the 2D hyperbolic truncated order-3 apeirogonal tiling, t{∞,3} with apeirogonal and triangle faces:
Bitruncated hexagonal tiling honeycomb[edit]
| Bitruncated hexagonal tiling honeycomb Bitruncated order-6 tetrahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | 2t{6,3,3} or t1,2{6,3,3} |
| Coxeter diagram | |
| Cells | t{3,3} t{3,6} |
| Faces | triangle {3} hexagon {6} |
| Vertex figure | 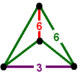 digonal disphenoid |
| Coxeter groups | , [3,3,6] , [3,3[3]] |
| Properties | Vertex-transitive |
The bitruncated hexagonal tiling honeycomb or bitruncated order-6 tetrahedral honeycomb, t1,2{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has truncated tetrahedron and hexagonal tiling cells, with a digonal disphenoid vertex figure.
has truncated tetrahedron and hexagonal tiling cells, with a digonal disphenoid vertex figure.
Cantellated hexagonal tiling honeycomb[edit]
| Cantellated hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | rr{6,3,3} or t0,2{6,3,3} |
| Coxeter diagram | |
| Cells | r{3,3} rr{6,3} {}×{3} |
| Faces | triangle {3} square {4} hexagon {6} |
| Vertex figure | 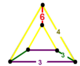 wedge |
| Coxeter groups | , [3,3,6] |
| Properties | Vertex-transitive |
The cantellated hexagonal tiling honeycomb, t0,2{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has octahedron, rhombitrihexagonal tiling, and triangular prism cells, with a wedge vertex figure.
has octahedron, rhombitrihexagonal tiling, and triangular prism cells, with a wedge vertex figure.
Cantitruncated hexagonal tiling honeycomb[edit]
| Cantitruncated hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | tr{6,3,3} or t0,1,2{6,3,3} |
| Coxeter diagram | |
| Cells | t{3,3} tr{6,3} {}×{3} |
| Faces | triangle {3} square {4} hexagon {6} dodecagon {12} |
| Vertex figure |  mirrored sphenoid |
| Coxeter groups | , [3,3,6] |
| Properties | Vertex-transitive |
The cantitruncated hexagonal tiling honeycomb, t0,1,2{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has truncated tetrahedron, truncated trihexagonal tiling, and triangular prism cells, with a mirrored sphenoid vertex figure.
has truncated tetrahedron, truncated trihexagonal tiling, and triangular prism cells, with a mirrored sphenoid vertex figure.
Runcinated hexagonal tiling honeycomb[edit]
| Runcinated hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t0,3{6,3,3} |
| Coxeter diagram | |
| Cells | {3,3} {6,3} {}×{6} {}×{3} |
| Faces | triangle {3} square {4} hexagon {6} |
| Vertex figure |  irregular triangular antiprism |
| Coxeter groups | , [3,3,6] |
| Properties | Vertex-transitive |
The runcinated hexagonal tiling honeycomb, t0,3{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has tetrahedron, hexagonal tiling, hexagonal prism, and triangular prism cells, with an irregular triangular antiprism vertex figure.
has tetrahedron, hexagonal tiling, hexagonal prism, and triangular prism cells, with an irregular triangular antiprism vertex figure.
Runcitruncated hexagonal tiling honeycomb[edit]
| Runcitruncated hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t0,1,3{6,3,3} |
| Coxeter diagram | |
| Cells | rr{3,3} {}x{3} {}x{12} t{6,3} |
| Faces | triangle {3} square {4} dodecagon {12} |
| Vertex figure | isosceles-trapezoidal pyramid |
| Coxeter groups | , [3,3,6] |
| Properties | Vertex-transitive |
The runcitruncated hexagonal tiling honeycomb, t0,1,3{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has cuboctahedron, triangular prism, dodecagonal prism, and truncated hexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure.
has cuboctahedron, triangular prism, dodecagonal prism, and truncated hexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure.
Runcicantellated hexagonal tiling honeycomb[edit]
| Runcicantellated hexagonal tiling honeycomb runcitruncated order-6 tetrahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t0,2,3{6,3,3} |
| Coxeter diagram | |
| Cells | t{3,3} {}x{6} rr{6,3} |
| Faces | triangle {3} square {4} hexagon {6} |
| Vertex figure |  isosceles-trapezoidal pyramid |
| Coxeter groups | , [3,3,6] |
| Properties | Vertex-transitive |
The runcicantellated hexagonal tiling honeycomb or runcitruncated order-6 tetrahedral honeycomb, t0,2,3{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has truncated tetrahedron, hexagonal prism, and rhombitrihexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure.
has truncated tetrahedron, hexagonal prism, and rhombitrihexagonal tiling cells, with an isosceles-trapezoidal pyramid vertex figure.
Omnitruncated hexagonal tiling honeycomb[edit]
| Omnitruncated hexagonal tiling honeycomb Omnitruncated order-6 tetrahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t0,1,2,3{6,3,3} |
| Coxeter diagram | |
| Cells | tr{3,3} {}x{6} {}x{12} tr{6,3} |
| Faces | square {4} hexagon {6} dodecagon {12} |
| Vertex figure | 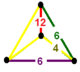 irregular tetrahedron |
| Coxeter groups | , [3,3,6] |
| Properties | Vertex-transitive |
The omnitruncated hexagonal tiling honeycomb or omnitruncated order-6 tetrahedral honeycomb, t0,1,2,3{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() has truncated octahedron, hexagonal prism, dodecagonal prism, and truncated trihexagonal tiling cells, with an irregular tetrahedron vertex figure.
has truncated octahedron, hexagonal prism, dodecagonal prism, and truncated trihexagonal tiling cells, with an irregular tetrahedron vertex figure.
See also[edit]
- Convex uniform honeycombs in hyperbolic space
- Regular tessellations of hyperbolic 3-space
- Paracompact uniform honeycombs
- Alternated hexagonal tiling honeycomb
References[edit]
- ^ Coxeter The Beauty of Geometry, 1999, Chapter 10, Table III
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space Archived 2016-06-10 at the Wayback Machine) Table III
- Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353 [1] [2]
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H3: p130. [3]
External links[edit]
- John Baez, Visual Insight: {6,3,3} Honeycomb (2014/03/15)
- John Baez, Visual Insight: {6,3,3} Honeycomb in Upper Half Space (2013/09/15)
- John Baez, Visual Insight: Truncated {6,3,3} Honeycomb (2016/12/01)