User:Marqaz/sandbox
Climate[edit]

The vast size, huge altitude range and complex topography of the Himalayas mean they experience a wide range of climates, from humid subtropical in the foothills to cold, dry desert conditions on the Tibetan side of the range.
For much of Himalayas - that on the south side of the high mountains, except in the furthest west, the most characteristic feature of the climate is the monsoon. Heavy rain arrives on the south-west monsoon in June, and persists until September. The monsoon can seriously impact transport and cause major landslides. It restricts tourism - the trekking and mountaineering season is limited to either before the monsoon in April/May or after the monsoon in October/November (autumn). In Nepal and Sikkim, there are often considered to be five seasons: summer, monsoon, autumn, winter and spring.
Using the Koppen climate classification, the lower elevations of the Himalayas, reaching in mid elevations in central Nepal (including the Kathmandu valley), are classified as Cwa, Humid subtropical climate with dry winters. Higher up, most of the Himalayas have a subtropical highland climate (Cwb).
In the furthest west of the Himalayas, in the west of the Kashmir valley and the Indus valley, the South Asian monsoon is no longer a dominant factor and most precipitation falls in the spring. Srinagar receives around 723 millimetres (28 in) around half the rainfall of locations such as Shimla and Kathmandu, with the wettest months being March and April.
The northern side of the Himalayas, also known as the Tibetan Himalaya, is dry, cold and generally wind swept particularly in the west where it has a cold desert climate. The vegetation is sparse and stunted and the winters are severely cold. Most of the snowfall is in the form of snow during late winter and spring months.
Local impacts on climate are significant throughout the Himalayas. Temperatures fall by 6.5 °C (11.7 °F) for every 1000m rise in altitude. This gives rise to a variety of climates from nearly tropical in the foothills to tundra and permanent snow and ice. The local climate can change within a few hundred metres. In Nepal and elsewhere, it is possible to recognise five climatic zones, broadly corresponding to altitude. The tropical and subtropical zones lie below 1,200 metres (3,937 ft), the temperate zone 1,200 to 2,400 metres (3,937 to 7,874 ft), the cold zone 2,400 to 3,600 metres (7,874 to 11,811 ft), the subarctic zone 3,600 to 4,400 metres (11,811 to 14,436 ft), and the Arctic zone above 4,400 metres (14,436 ft).
Altitude also affects rainfall: areas situated at elevations of 1,000–2,400 metres receive the heaviest rainfall, which decreases rapidly at elevations above 2400m. Local climate can also be affected by the topography: The leeward side of the mountains receive less rain while the well exposed slopes get heavy rainfall and the rain shadow of large mountains can be significant, for example leading to near desert conditions in the Upper Mustang. There can also be significant temperature contrasts between sunny and shady slopes.
India's northernmost areas are subject to a montane, or alpine, climate. The area to the south of the Himalayan range is protected from cold winds coming from interior of Asia during winter. . The great Himalayan range witnesses heavy snowfall during winter months of December to February at altitudes above 1500m. The diurnal range of temperature is also high.
Most precipitation occurs as snowfall during the late winter and spring months.The Himalayas experience their heaviest snowfall between December and February and at elevations above 1,500 metres (4,921 ft). Snowfall increases with elevation by up to several dozen millimetres per 100 metre (~2 in; 330 ft) increase. Elevations above 6,000 metres (19,685 ft) never experience rain; all precipitation falls as snow.[1] The temperature during the coldest months in regions experiencing this climate falls between 18 and 0 °C.
- Sub-tropical humid (wet) with dry winters
In the foothills of the Himalayas, The rainfall is received mostly in the summer and is about 65 cm in the west and increases to 250 cm annually to the east and near the Himalayas. The winters are mainly dry due to the land derived winter winds which blow down the lowlands of north India towards the Bay of Bengal. The summers are hot and temperatures can reach 46 °C in the lowlands. May and June are the hottest months. Winter months are mostly dry with feeble winds. Frost occurs for a few weeks in winter. The difference in rainfall between the east and the west gives rise to a wide difference in the natural vegetation.
- Mountain climate or highland climate or alpine climate
In the Himalayan mountains the temperature falls by 0.6 °C for every 100 m rise in altitude and One can also observe sharp contrast between temperatures of the sunny and shady slopes, high diurnal range of temperature, inversion of temperature, and variability of rainfall based on altitude.
Thimphu experiences a southwest monsoon-influenced Subtropical highland climate (Cwb) of a warm, temperate climate. The southwest monsoon rainfall occurs during mid-June to September. Lightning and thunder often precedes rainfall in the region with cumulonimbus clouds and light showers dominating the weather.[2][3] Continuous rainfall for several days occurs resulting in landslides and blockage of roads. Streams and rivers swell up carrying huge amounts of debris from forests. Deep puddles, thick mud, and landslides along roads form barriers to transportation. Cold winds, low temperatures at night, and moderate temperatures during the day, cloudiness, light showers and snowfall mark winter weather in this zone. Fog causes poor visibility, which poses a threat to vehicular traffic in the city.[2][3] As spring approaches, the landscape is marked by violent winds and relatively dry and clear skies.[2][3]
Thimphu experiences a wet season, which runs from May through September and a dry season that covers the remainder of the year. Rainfall in the valley varies between 500 millimetres (20 in) and 1,000 millimetres (39 in) per year, the bulk of which is received during the monsoonal wet season. The average temperature recorded during winter varies between 5–15 °C (41–59 °F) while in summer the variation is between 15–30 °C (59–86 °F).[2][3][4] The coldest average (minimum) temperature in January is −2.6 °C (27.3 °F) and the average highest temperature recorded during August is 25 °C (77 °F).
The Himalaya blocks cold winds from Central Asia in the winter and forms the northern limit of the monsoon wind patterns.
Sikkim has five seasons: winter, summer, spring, autumn, and a monsoon season between June and September. Sikkim's climate ranges from sub-tropical in the south to tundra in the north. Most of the inhabited regions of Sikkim experience a temperate climate, with temperatures seldom exceeding 28 °C (82 °F) in summer. The average annual temperature for most of Sikkim is around 18 °C (64 °F).
Sikkim is one of the few states in India to receive regular snowfall. The snow line ranges from 6,100 metres (20,000 ft) in the south of the state to 4,900 metres (16,100 ft) in the north.[5] The tundra-type region in the north is snowbound for four months every year, and the temperature drops below 0 °C (32 °F) almost every night.[6] In north-western Sikkim, the peaks are frozen year-round;[7] because of the high altitude, temperatures in the mountains can drop to as low as −40 °C (−40 °F) in winter.
During the monsoon, heavy rains increase the risk of landslides. The record for the longest period of continuous rain in Sikkim is 11 days. Fog affects many parts of the state during winter and the monsoons, making transportation perilous.[8]
The climate of Jammu and Kashmir varies greatly owing to its rugged topography. In the south around Jammu, the climate is typically monsoonal, though the region is sufficiently far west to average 40 to 50 mm (1.6 to 2 inches) of rain per month between January and March. In the hot season, Jammu city is very hot and can reach up to 40 °C (104 °F) whilst in July and August, very heavy though erratic rainfall occurs with monthly extremes of up to 650 millimetres (25.5 inches). In September, rainfall declines, and by October conditions are hot but extremely dry, with minimal rainfall and temperatures of around 29 °C (84 °F).
Geography and key features[edit]
In the middle of great curve of the Himalayan mountains lie the 8000m peaks of Dhaulagiri and Annapurna in Nepal, separated by the Kali Gandaki Gorge. The gorge splits the Himalayas into Western and Eastern sections both ecologically and orographically - the pass at the head of the Kali Gandaki, the Kora La is the lowest point on the ridgeline between Everest and K2. To the east of Annapurna are the 8000m peaks of Manaslu and across the border in Tibet, Shishapangma. To the south of these lies Kathmandu, the capital of Nepal and the largest city in the Himalayas. East of the Kathmandu Valley lies valley of the Bhote/Sun Kosi river which rises in Tibet and provides the main overland route between Nepal and China - the Araniko Highway/China National Highway 318. Further east is the Mahalangur Himal with 4 of the world's 6 highest mountains, including the highest: Cho Oyu, Everest, Lhotse and Makalu. The Khumbu region, popular for trekking, is found here on the south-western approaches to Everest. The Arun river drains the northern slopes of these mountains, before turning south and flowing through the range to the east of Makalu.
In the far east of Nepal the Himalayas rise to the Kanchenjunga massif on the border with India, the third highest mountain in the world, the most easterly 8000m summit and the highest point of India. The eastern side of Kanchenjunga is in the Indian state of Sikkim, Formerly an independent Kingdom, it lies on the main route from India to Lhasa, Tibet, which passes over the Nathu La pass into Tibet. East of Sikkim lies the ancient Buddhist Kingdom of Bhutan. The highest mountain in Bhutan is Gangkhar Puensum, which is also a strong candidate for the highest unclimbed mountain in the world. The Himalayas here are becoming increasingly rugged with heavily forested steep valleys. The Himalayas continue, turning slightly north east, through the disputed Indian State of Arunachal Pradesh as well as Tibet, before reaching their easterly conclusion in the peak of Namche Barwa, situated in Tibet inside the great bend of the Yarlang Tsangpo river. The high mountains the other side of the Tsangpo including Gyala Peri are also sometimes also included the Himalayas.
Going west from Dhaulagiri, Western Nepal is somewhat remote and lacks major high mountains, but is home to Rara Lake, the largest lake in Nepal. The Karnali River rises in Tibet but cuts through the centre of the region. Further west, the border with India follows the Sarda River and provides a trade route into China, where on the Tibetan plateau lies the high peak of Gurla Mandhata. Just across Lake Manasarovar from this lies the sacred Mount Kailash, which stands close to the source of the four main rivers of Himalayas and is revered in Hinduism, Buddhism, Jainism and Bonpo. In the newly created Indian state of Uttarkhand, the Himalayas rise again as the Garwhal Himalayas with the high peaks of Nanda Devi and Kamet . The state is also an important pilgrimage destination, with the source of the Ganges at Gangotri and the Yamuna at Yamunotri, and the temples at Badrinath and Kedarnath.
The next Himalayan Indian state, Himachal Pradesh lacks really high mountains, but is noted for natural beauty and its hill stations, particular Shimla. the summer capital of the British Raj, and Dharmasala, the centre of the Tibetan community in exile in India. This area marks the start of the Punjab Himalaya and the Sutlej river, the most easterly of the five tributaries of the Indus, cuts through the range here. Further west, the Himalayas form most of the southern portion of the disputed Indian State of Jammu & Kashmir. The twin peaks of Nun Kun are the only mountains over 7000m in this part of the Himalayas. Beyond lies the renown Kashmir Valley and the town and lakes of Srinagar. Finally, the Himalayas cross the Line of Control into Pakistan and reach their western end in the dramatic 8000m peak of Nanga Parbat, which rises over 7000m above the Indus valley and is the most westerly of the 8000m summits.
Significant mountains of the Himalayas[edit]
| Year | Event |
|---|---|
| 1768 | Kingdom of Nepal established |
| 1947 | Partition of India/ India and Pakistan Independence |
| 1951 | Tibet integrated into Peoples Republic of China |
| 1953 | Everest Climbed |
| 1962 | Indo-Chinese War, China invades Aranachal Pradesh but later withdraws. |
| 1975 | Sikkim becomes a state of India |
| 1992 | Namche Barwa first ascent |
| 2008 | Nepal becomes a republic |
| 2009 | Uttarkhand created as a separate state in India |
Elliptical orbit[edit]
Table of orbital formula[edit]
Under standard assumptions
| Element | Symbol | Formula | Alternative formula |
|---|---|---|---|
| standard gravitational parameter | |||
| Eccentricity | |||
| Semi-major axis | |||
| Periapsis distance | |||
| Apoapsis distance | |||
| Semi-latus rectum | |||
| Average distance (by time) | |||
| Orbital period | |||
| Specific orbital energy | |||
| Specific angular momentum | |||
| Variables | |||
| Distance between the orbiting bodies | |||
| orbital speed |
The velocity equation for a hyperbolic trajectory has either + , or it is the same with the convention that in that case a is negative. Vis-viva equation
Conclusions:
- The orbital period is equal to that for a circular orbit with the orbital radius equal to the semi-major axis (),
- For a given semi-major axis the orbital period does not depend on the eccentricity (See also: Kepler's third law).
Energy[edit]
Under standard assumptions, specific orbital energy () of elliptic orbit is negative and the orbital energy conservation equation (the Vis-viva equation) for this orbit can take the form:
where:
- is the orbital speed of the orbiting body,
- is the distance of the orbiting body from the central body,
- is the length of the semi-major axis,
- is the standard gravitational parameter.
Conclusions:
| Eccentricity | |||||||
|---|---|---|---|---|---|---|---|
| .01 | .05 | .10 | .20 | .50 | .85 | .99 | |
| Periapsis distance | 99 | 95 | 90 | 80 | 50 | 15 | 1 |
| Apoapsis distance | 101 | 105 | 110 | 120 | 150 | 185 | 199 |
| Semi-latus rectum | 99.99 | 99.75 | 99 | 96 | 75 | 27.75 | 1.99 |
| Minor axis | 99.99 | 99.87 | 99.50 | 97.98 | 86.60 | 52.68 | 14.11 |
| Average Distance | 100.01 | 100.25 | 101.00 | 104.00 | 125.00 | 172.25 | 198.01 |
| Max speed | 101.01 | 105.13 | 110.55 | 122.47 | 173.21 | 351.19 | 1411 |
| Min speed | 99.00 | 95.12 | 90.45 | 81.65 | 57.74 | 28.47 | 7.09 |
| % orbit by time where r<a | 50% | 48% | 47% | 44% | 34% | 23% | 18% |
| % orbit by time where r<p | 49% | 47% | 44% | 37% | 20% | 3% | 0.1% |
| Ratio of distance or speed | 1.020 | 1.105 | 1.222 | 1.50 | 3.0 | 12.33 | 199 |
| Ratio of energy or irradiation | 1.041 | 1.222 | 1.494 | 2.25 | 9.0 | 152.11 | 39601 |
| Examples | Earth (.017) | Moon (.055) Jupiter (.048) |
Mars (0.093) | Mercury (0.21) | Eris (0.44) | Sedna (0.85) | Comets |
Parameters describing a Hyperbolic trajectory[edit]
Like an elliptical orbit, a hyperbolic trajectory for a given system can be defined (ignoring orientation) by its semi major axis and the eccentricity . However, with a hyperbolic orbit other parameters may more useful in understanding a body's motion. The following table lists the main parameters describing the path of body following a hyperbolic trajectory around another under standard assumptions and the formula connecting them.
| Element | Symbol | Formula | using (or ), and |
|---|---|---|---|
| Standard gravitational parameter | |||
| Eccentricity (>1) | |||
| Semi-major axis (<0) | |||
| Hyperbolic excess velocity | |||
| (External) Angle between asymptotes | |||
| Impact parameter (Semi-minor axis) | |||
| Semi-latus rectum | |||
| Periapsis distance | |||
| Specific orbital energy | |||
| Specific angular momentum |
Semi-major axis, energy and hyperbolic excess velocity[edit]
The semi major axis () is not immediately visible with an hyperbolic trajectory but can be constructed as it is the distance from periapsis to the point where the two asymptotes cross. Usually, by convention, it is negative, to keep various equations are consistent with elliptical orbits.
The semi major axis is directly linked to the specific orbital energy () or characteristic energy of the orbit, and to the velocity the body attains at as the distance tends to infinity, the hyperbolic excess velocity ().
- or
where: is the standard gravitational parameter and is characteristic energy, commonly used in planning interplanetary missions
Note that the total energy is positive in the case of a hyperbolic trajectory (whereas it is negative for an elliptical orbit).
Eccentricity and angle between approach and departure[edit]
With a hyperbolic trajectory the orbital eccentricity () is greater than 1. The eccentricity is directly related to the angle between the asymptotes. With eccentricity just over 1 the hyperbola is a sharp "v" shape. At the asymptotes are at right angles. With the asymptotes are more that 120° apart, and the periapsis distance is greater than the semi major axis. As eccentricity increases further the motion approaches a straight line.
The angle between the direction of periapsis and an asymptote from the central body is the true anomaly as distance tends to infinity (), , so is the external angle between approach and departure directions (between asymptotes). Then
- or
Impact Parameter and the distance of closest approach[edit]
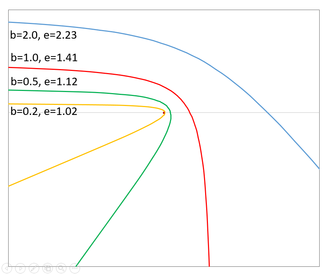
The impact parameter is the distance by which a body, if it continued on an unperturbed path, would miss the central body at its closest approach. With bodies experiencing gravitational forces and following hyperbolic trajectories it is equal to the semi-minor axis of the hyperbola.
In the situation of a spacecraft or comet approaching a planet, the impact parameter and excess velocity will be known accurately. If the central body is known the trajectory can now be found, including how close the approaching body will be at periapsis. If this is less than planet's radius an impact should be expected. The distance of closest approach, or periapse distance, is given by:
So with a comet approaching Earth (effective radius ~6400km) with an velocity of 12.5 km/s (the approximate minimum approach speed of a body coming from the outer solar system) is to avoid a collision with Earth, the impact parameter will need to be at least 8600km, or 34% more than the Earth's radius. A body approaching Jupiter (radius 70000km) from the outer solar system with a speed of 5.5 km/h, will need the impact parameter to be at least 770,000km or 11 times the radius of Jupiter to avoid collision.
If the mass of central body is not known then its standard gravitational parameter and hence is mass can be determined by the deflection of the smaller body, together with its impact parameter and approach speed. As, typically, all these variables can be determined accurately, a spacecraft flyby will provide a good estimate of mass.
- where is the angle the smaller body is deflected from a straight line in its course.
http://www.braeunig.us/space/orbmech.htm http://aa.quae.nl/en/reken/kepler.html http://www.bogan.ca/orbits/kepler/orbteqtn.html
Equations of motion[edit]
Position[edit]
In a hyperbolic trajectory the true anomaly is linked to the distance between the orbiting bodies () by the orbit equation:
The relation between the true anomaly θ and the eccentric anomaly E is:
- or
The eccentric anomaly E is related to the mean anomaly M by Kepler's equation:
The mean anomaly is proportional to time
- where μ is a gravitational parameter w and a is the semi-major axis of the orbit.
Velocity[edit]
Under standard assumptions the orbital speed () of a body traveling along a hyperbolic trajectory can be computed from the vis-viva equation as:
Under standard assumptions, at any position in the orbit the following relation holds for orbital velocity (), local escape velocity () and hyperbolic excess velocity ():
Note that this means that a relatively small extra delta-v above that needed to accelerate to the escape speed results in a relatively large speed at infinity. For example, at a place where escape speed is 11.2 km/s, the addition of 0.4 km/s yields a hyperbolic excess speed of 3.02 km/s.
This is an example of the Oberth effect. The converse is also true - a body does not need to be slowed by much compared to its hyperbolic excess speed (e.g. by atmospheric drag near periapsis) for velocity to fall below escape velocity and so for the body to be captured.
table of living bear species[edit]
| Binomial Name | Common Name | Size | Distribution | IUCN classification |
Diet |
|---|---|---|---|---|---|
| Ursus maritimus | Polar Bear | M:350–700kg | Arctic | Seals | |
| Ursus arctos | Brown bear (subsp: Grizzly bear, Kodiak bear) |
100-700kg | Northern Eurasia, North America | Omnivorous | |
| Ursus americanus | American black bear | M:57–250kg F:41–170 kg |
North America | Omnivorous | |
| Ursus thibetanus | Asian black bear (Moon bear, White-chested bear) |
M:100–200 kg F:65–90 kg |
NE Asia, China, Himalayas | Omnivorous | |
| Melursus ursinus | Sloth bear (Stickney bear, Labiated bear) | M:80-192kg F:55-124kg |
Indian sub-continent | Termites, bees, fruits | |
| Helarctos malayanus | Sun bear | 27-65kg | South-east Asia | Bees/honey, insects, fruits | |
| Tremarctos ornatus | Spectacled bear (Andean bear) | M:100–200kg F:35–82 kg |
South America | Vegetation, some meat | |
| Ailuropoda melanoleuca | Giant Panda | M: 100-160kg F:75-125kg |
China | Bamboo |
Construction of a map projection[edit]
| type | Conformal | Equal Area | Equidistant | Compromise |
|---|---|---|---|---|
| Cylindrical | Mercator | Gall-Peters | Plate Carree | |
| Pseudocylindrical | none | several Sinusoidal Mollweide | (sinusoidal) | Robinson |
| Conical | Conformal | Albers | Equidistant | |
| Azimuthal | Stereographic | Lambert | Equidistant |
Some of the simplest map projections are literally projections, and are obtained by placing a light source at some definite point relative to the globe and projecting its features onto a specified surface. This is not the case for many projections, which are defined only in terms of mathematical formulae that have no direct geometric interpretation.
A surface that can be unfolded or unrolled into a plane or sheet without stretching, tearing or shrinking is called a developable surface. The cylinder, cone and of course the plane are all developable surfaces. The sphere and ellipsoid do not have developable surfaces, so any projection of them onto a plane will have to distort the image. (To compare, one cannot flatten an orange peel without tearing and warping it.) One way of describing a projection is first to project from the Earth's surface to a developable surface such as a cylinder or cone, and then to unroll the surface into a plane. While the first step inevitably distorts some properties of the globe, the developable surface can then be unfolded without further distortion. The three developable surfaces (plane, cylinder, cone) provide useful models for understanding, describing, and developing many map projections. However, these models are limited in two fundamental ways. For one thing, most world projections in actual use do not fall into any of those categories. For another thing, even most projections that do fall into those categories are not naturally attainable through physical projection.
Using a projection surface[edit]
The creation of a map projection involves two steps
As L.P. Lee notes,
- Selection of a model for the shape of the Earth or planetary body (usually choosing between a sphere or ellipsoid). Because the Earth's actual shape is irregular, information is lost in this step.
- Transformation of geographic coordinates (longitude and latitude) to Cartesian (x,y) or polar plane coordinates. Cartesian coordinates normally have a simple relation to eastings and northings defined on a grid superimposed on the projection.
No reference has been made in the above definitions to cylinders, cones or planes. The projections are termed cylindric or conic because they can be regarded as developed on a cylinder or a cone, as the case may be, but it is as well to dispense with picturing cylinders and cones, since they have given rise to much misunderstanding. Particularly is this so with regard to the conic projections with two standard parallels: they may be regarded as developed on cones, but they are cones which bear no simple relationship to the sphere. In reality, cylinders and cones provide us with convenient descriptive terms, but little else.[14]
Lee's objection refers to the way the terms cylindrical, conic, and planar (azimuthal) have been abstracted in the field of map projections. If maps were projected as in light shining through a globe onto a developable surface, then the spacing of parallels would follow a very limited set of possibilities. Such a cylindrical projection (for example) is one which:
- Is rectangular;
- Has straight vertical meridians, spaced evenly;
- Has straight parallels symmetrically placed about the equator;
- Has parallels constrained to where they fall when light shines through the globe onto the cylinder, with the light source someplace along the line formed by the intersection of the prime meridian with the equator, and the center of the sphere.
(If you rotate the globe before projecting then the parallels and meridians will not necessarily still be straight lines. Rotations are normally ignored for the purpose of classification.)
Where the light source emanates along the line described in this last constraint is what yields the differences between the various "natural" cylindrical projections. But the term cylindrical as used in the field of map projections relaxes the last constraint entirely. Instead the parallels can be placed according to any algorithm the designer has decided suits the needs of the map. The famous Mercator projection is one in which the placement of parallels does not arise by "projection"; instead parallels are placed how they need to be in order to satisfy the property that a course of constant bearing is always plotted as a straight line.
Aspects of the projection[edit]
Once a choice is made between projecting onto a cylinder, cone, or plane, the aspect of the shape must be specified. The aspect describes how the developable surface is placed relative to the globe: it may be normal (such that the surface's axis of symmetry coincides with the Earth's axis), transverse (at right angles to the Earth's axis) or oblique (any angle in between). The developable surface may also be either tangent or secant to the sphere or ellipsoid. Tangent means the surface touches but does not slice through the globe; secant means the surface does slice through the globe. Moving the developable surface away from contact with the globe never preserves or optimizes metric properties, so that possibility is not discussed further here.
Scale[edit]
A globe is the only way to represent the earth with constant scale throughout the entire map in all directions. A map cannot achieve that property for any area, no matter how small. It can, however, achieve constant scale along specific lines.
Some possible properties are:
- The scale depends on location, but not on direction. This is equivalent to preservation of angles, the defining characteristic of a conformal map.
- Scale is constant along any parallel in the direction of the parallel. This applies for any cylindrical or pseudocylindrical projection in normal aspect.
- Combination of the above: the scale depends on latitude only, not on longitude or direction. This applies for the Mercator projection in normal aspect.
- Scale is constant along all straight lines radiating from a particular geographic location. This is the defining characteristic of an equidistant projection such as the Azimuthal equidistant projection. There are also projections (Maurer, Close) where true distances from two points are preserved.[15][16]
Choosing a model for the shape of the Earth[edit]
Projection construction is also affected by how the shape of the Earth is approximated. In the following section on projection categories, the earth is taken as a sphere in order to simplify the discussion. However, the Earth's actual shape is closer to an oblate ellipsoid. Whether spherical or ellipsoidal, the principles discussed hold without loss of generality.
Selecting a model for a shape of the Earth involves choosing between the advantages and disadvantages of a sphere versus an ellipsoid. Spherical models are useful for small-scale maps such as world atlases and globes, since the error at that scale is not usually noticeable or important enough to justify using the more complicated ellipsoid. The ellipsoidal model is commonly used to construct topographic maps and for other large- and medium-scale maps that need to accurately depict the land surface.
A third model of the shape of the Earth is the geoid, a complex and more accurate representation of the global mean sea level surface that is obtained through a combination of terrestrial and satellite gravity measurements. This model is not used for mapping because of its complexity, but rather is used for control purposes in the construction of geographic datums. (In geodesy, plural of "datum" is "datums" rather than "data".) A geoid is used to construct a datum by adding irregularities to the ellipsoid in order to better match the Earth's actual shape. It takes into account the large-scale features in the Earth's gravity field associated with mantle convection patterns, and the gravity signatures of very large geomorphic features such as mountain ranges, plateaus and plains.
Historically, datums have been based on ellipsoids that best represent the geoid within the region that the datum is intended to map. Controls (modifications) are added to the ellipsoid in order to construct the datum, which is specialized for a specific geographic region (such as the North American Datum). A few modern datums, such as WGS84 which is used in the Global Positioning System, are optimized to represent the entire earth as well as possible with a single ellipsoid, at the expense of accuracy in smaller regions.
Classification[edit]
A fundamental projection classification is based on the type of projection surface onto which the globe is conceptually projected. The projections are described in terms of placing a gigantic surface in contact with the earth, followed by an implied scaling operation. These surfaces are cylindrical (e.g. Mercator), conic (e.g., Albers), or azimuthal or plane (e.g. stereographic). Many mathematical projections, however, do not neatly fit into any of these three conceptual projection methods. Hence other peer categories have been described in the literature, such as pseudoconic, pseudocylindrical, pseudoazimuthal, retroazimuthal, and polyconic.
Another way to classify projections is according to properties of the model they preserve. Some of the more common categories are:
- Preserving direction (azimuthal), a trait possible only from one or two points to every other point
- Preserving shape locally (conformal or orthomorphic)
- Preserving area (equal-area or equiareal or equivalent or authalic)
- Preserving distance (equidistant), a trait possible only between one or two points and every other point
- Preserving shortest route, a trait preserved only by the gnomonic projection
Because the sphere is not a developable surface, it is impossible to construct a map projection that is both equal-area and conformal.
Projections by surface[edit]
Pseudocylindrical[edit]

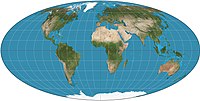

Pseudocylindrical projections map parallels as straight lines and represent the central meridian as a straight line segment. Other meridians are longer than the central meridian and bow outward away from the central meridian. Along parallels, each point from the surface is mapped at a distance from the central meridian that is proportional to its difference in longitude from the central meridian, i.e. meridians are evenly spaced. Pseudocylindrical projections can be expressed mathematically as the form:
where is the longitude from the central meridian, is the latitude and and functions.
Pseudocylindrical projections are most commonly used for displaying the whole world. Many pseudocylindrical projections are equal area, others are compromise projections, but none can be conformal. On a pseudocylindrical map, north-south relationships are preserved, so any point further from the equator on the map than some other point has a higher latitude than the other point. This trait is useful when illustrating phenomena that depend on latitude, such as climate. Examples of psuedocylindrial projections include:
- Sinusoidal, which was the first pseudocylindrical projection developed. Vertical scale and horizontal scale are the same throughout, resulting in an equal-area map. On the map, as in reality, the length of each parallel is proportional to the cosine of the latitude. Thus the shape of the map for the whole earth is the region between two symmetric rotated cosine curves.[17] The true distance between two points on the same meridian corresponds to the distance on the map between the two parallels, which is smaller than the distance between the two points on the map. The distance between two points on the same parallel is true. The area of any region is true. However there is significant distortion away from the equator and central meridian.
- The Mollweide projection is another early pseudocylindrical projection, dating from 1805. Meridians are mapped as ellipses and parallels are no longer evenly spaced, but it is equal area. The area of high distortion is generally reduced compared to the Sinusoidal, and it has a "pleasant" overall shape.[18]
- The Robinson projection. This is an example of a compromise pseudocylindrical projection - no longer equal area, but with the aim of reducing distortion overall. It also maps the poles as straight lines - "flat polar" - a feature of a number of pseudocylindrical projections, which can help reduce shearing distortion at high latitudes.
Interrupted and Hybrid forms[edit]
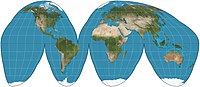
Pseudocylindrical projections are particularly suitable for displaying in interrupted form: typically dividing along one of the meridians, usually from the pole to the equator, and with a number of primary meridians as a result. This significantly reduces distortion, at the expense of a more complex shape and the loss of relationship between points either side of a cut. Interruption is commonly used when the focus is primarily on the land masses (or, more rarely, primarily on the oceans).
Two pseudocylindrical (or a pseudocylindrical and cylindrical) projections can also be combined, most usually by matching scale along parallels, to form a hybrid projection. An example of both approaches is the usual presentation of Goode homolosine projection, which uses the sinusoidal projection in equatorial regions and Mollweide projection in higher latitudes. The HEALPix projection is a more recent example, combining a cylindrical equal area projection in equatorial regions with an interrupted Collignon projection at higher altitudes.
Conical[edit]

A conic projection is a projection in which meridians are mapped to equally spaced lines radiating out from the apex and circles of latitude (parallels) are mapped to circular arcs centered on the apex. However, compared to the sphere, the angular distance between meridians in reduced, by a set factor the cone constant. [19]
When making a conic map, the map maker selects two (or one) standard parallels. Those standard parallels may be visualized as secant lines where the cone intersects the globe — or, if the map maker chooses the same parallel twice, as the tangent line where the cone is tangent to the globe. The resulting conic map has low distortion in scale, shape, and area near those standard parallels. Conical maps (in the normal aspect) can portray large areas of temperate latitudes with low to moderate distortion making them a common choice for maps of America and Europe for example.
However, distances along the parallels to the north of both standard parallels or to the south of both standard parallels are necessarily stretched and distortion rapidly increases away from the reference parallels, becoming extreme in the opposite hemisphere. This limits their use without modification for larger areas.
The most popular conic maps either
- Albers conic
- compress north-south distance between each parallel to compensate for the east-west stretching, giving an equal-area map, or
- Equidistant conic
- keep constant distance scale along the entire meridian, typically the same or near the scale along the standard parallels, or
- Lambert conformal conic
- stretch the north-south distance between each parallel to equal the east-west stretching, giving a conformal map.
Most common conic projections are not perspective projections, including these three. A perpsective projection is the Braun stereograhic conic projection but it is rarely used.
Pseudoconical[edit]
Pseudocylindrical maps have circular concentrical parallels, but meridians other than the prime meridian are curved (in a manner analagous to pseudoscylindrical maps.) Pseudoconical maps have be known since ancient times, predating pseudocylindrical maps. Psuedoconical maps can display the whole world with moderate disotrtion but have unusual outlines.
- Collignon projection which in its most common forms represents each meridian as 2 straight line segments, one from each pole to the equator.
{|
||
||
|}
- ^ Singh & Kumar 1997.
- ^ a b c d Cite error: The named reference
Dzongkhagwas invoked but never defined (see the help page). - ^ a b c d Cite error: The named reference
Naturalwas invoked but never defined (see the help page). - ^ "Weatherbase". Weatherbase. Retrieved 2010-06-07.
- ^ Hooker, Joseph Dalton (1854). Himalayan Journals: Notes of a Naturalist (version 2 ed.). John Murray. p. 396.
- ^ Choudhury 2006, p. 11.
- ^ Choudhury 2006, p. 13.
- ^ Hooker p. 409
- ^ For Nepal, the heights indicated on the Nepal Topographic Maps are followed. For China, the heights are those of "The Maps of Snow Mountains in China". Elsewhere, unless otherwise indicated, heights are those in Jill Neate's "High Asia".
- ^ Prominences over 1,500 m were copied from the the Ultra Project Prominence Lists, the remainder corresponds to those listed in this table of all mountains above 6650 m
- ^ Sorts by Longitude. Coordinates were established by comparing topographical maps with satellite images and SRTM-derived terrain maps. The terrain maps and satellite images often don't match exactly. An asterisk (*) indicates that the map and image are shifted by more than 100 m (4") and/or that the landscapes around the summit don't match.
- ^ Cho Oyu's height is 8,188 m according to the Nepal Survey's 1996 topographical map H8615, which represents the best known measurement to date. Previous estimates have been 8,153 m and 8,201 m
- ^ The name and information about this summit was extracted from the May 2003 edition of Japanese Alpine News.
- ^ Lee, L.P. (1944). "The nomenclature and classification of map projections". Empire Survey Review. VII (51): 190–200. p. 193
- ^ Snyder, John P. (1993). Flattening the earth: two thousand years of map projections. University of Chicago Press. ISBN 0-226-76746-9.
- ^ Snyder, John P. (1997). Flattening the earth: two thousand years of map projections. University of Chicago Press. ISBN 978-0-226-76747-5.
- ^ Weisstein, Eric W. "Sinusoidal Projection". MathWorld.
- ^ http://www.progonos.com/furuti/MapProj/Normal/ProjPCyl/projPCyl.html retrieved 20th April 2012
- ^ Carlos A. Furuti. "Conic Projections"
Cite error: There are <ref group=dp> tags on this page, but the references will not show without a {{reflist|group=dp}} template (see the help page).