In mathematics , a jacket matrix is a square symmetric matrix
A
=
(
a
i
j
)
{\displaystyle A=(a_{ij})}
n if its entries are non-zero and real , complex , or from a finite field , and
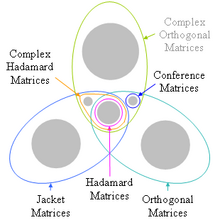
Hierarchy of matrix types
A
B
=
B
A
=
I
n
{\displaystyle \ AB=BA=I_{n}}
where I n identity matrix , and
B
=
1
n
(
a
i
j
−
1
)
T
.
{\displaystyle \ B={1 \over n}(a_{ij}^{-1})^{T}.}
where T denotes the transpose of the matrix.
In other words, the inverse of a jacket matrix is determined by its element-wise or block-wise inverse. The definition above may also be expressed as:
∀
u
,
v
∈
{
1
,
2
,
…
,
n
}
:
a
i
u
,
a
i
v
≠
0
,
∑
i
=
1
n
a
i
u
−
1
a
i
v
=
{
n
,
u
=
v
0
,
u
≠
v
{\displaystyle \forall u,v\in \{1,2,\dots ,n\}:~a_{iu},a_{iv}\neq 0,~~~~\sum _{i=1}^{n}a_{iu}^{-1}\,a_{iv}={\begin{cases}n,&u=v\\0,&u\neq v\end{cases}}}
The jacket matrix is a generalization of the Hadamard matrix ; it is a diagonal block-wise inverse matrix.
n .... −2, −1, 0 1, 2,.....
logarithm
2n
....
1
4
,
1
2
,
{\displaystyle \ {1 \over 4},{1 \over 2},}
series
As shown in the table, i.e. in the series, for example with n =2, forward:
2
2
=
4
{\displaystyle 2^{2}=4}
inverse :
(
2
2
)
−
1
=
1
4
{\displaystyle (2^{2})^{-1}={1 \over 4}}
4
∗
1
4
=
1
{\displaystyle 4*{1 \over 4}=1}
A
=
[
1
1
1
1
1
−
2
2
−
1
1
2
−
2
−
1
1
−
1
−
1
1
]
,
{\displaystyle A=\left[{\begin{array}{rrrr}1&1&1&1\\1&-2&2&-1\\1&2&-2&-1\\1&-1&-1&1\\\end{array}}\right],}
B
=
1
4
[
1
1
1
1
1
−
1
2
1
2
−
1
1
1
2
−
1
2
−
1
1
−
1
−
1
1
]
.
{\displaystyle B={1 \over 4}\left[{\begin{array}{rrrr}1&1&1&1\\[6pt]1&-{1 \over 2}&{1 \over 2}&-1\\[6pt]1&{1 \over 2}&-{1 \over 2}&-1\\[6pt]1&-1&-1&1\\[6pt]\end{array}}\right].}
or more general
A
=
[
a
b
b
a
b
−
c
c
−
b
b
c
−
c
−
b
a
−
b
−
b
a
]
,
{\displaystyle A=\left[{\begin{array}{rrrr}a&b&b&a\\b&-c&c&-b\\b&c&-c&-b\\a&-b&-b&a\end{array}}\right],}
B
=
1
4
[
1
a
1
b
1
b
1
a
1
b
−
1
c
1
c
−
1
b
1
b
1
c
−
1
c
−
1
b
1
a
−
1
b
−
1
b
1
a
]
,
{\displaystyle B={1 \over 4}\left[{\begin{array}{rrrr}{1 \over a}&{1 \over b}&{1 \over b}&{1 \over a}\\[6pt]{1 \over b}&-{1 \over c}&{1 \over c}&-{1 \over b}\\[6pt]{1 \over b}&{1 \over c}&-{1 \over c}&-{1 \over b}\\[6pt]{1 \over a}&-{1 \over b}&-{1 \over b}&{1 \over a}\end{array}}\right],}
For m x m matrices,
A
j
,
{\displaystyle \mathbf {A_{j}} ,}
A
j
=
d
i
a
g
(
A
1
,
A
2
,
.
.
A
n
)
{\displaystyle \mathbf {A_{j}} =\mathrm {diag} (A_{1},A_{2},..A_{n})}
J
4
=
[
I
2
0
0
0
0
cos
θ
−
sin
θ
0
0
sin
θ
cos
θ
0
0
0
0
I
2
]
,
{\displaystyle J_{4}=\left[{\begin{array}{rrrr}I_{2}&0&0&0\\0&\cos \theta &-\sin \theta &0\\0&\sin \theta &\cos \theta &0\\0&0&0&I_{2}\end{array}}\right],}
J
4
T
J
4
=
J
4
J
4
T
=
I
4
.
{\displaystyle \ J_{4}^{T}J_{4}=J_{4}J_{4}^{T}=I_{4}.}
Euler's formula :
e
i
π
+
1
=
0
{\displaystyle e^{i\pi }+1=0}
e
i
π
=
cos
π
+
i
sin
π
=
−
1
{\displaystyle e^{i\pi }=\cos {\pi }+i\sin {\pi }=-1}
e
−
i
π
=
cos
π
−
i
sin
π
=
−
1
{\displaystyle e^{-i\pi }=\cos {\pi }-i\sin {\pi }=-1}
Therefore,
e
i
π
e
−
i
π
=
(
−
1
)
(
1
−
1
)
=
1
{\displaystyle e^{i\pi }e^{-i\pi }=(-1)({\frac {1}{-1}})=1}
Also,
y
=
e
x
{\displaystyle y=e^{x}}
d
y
d
x
=
e
x
{\displaystyle {\frac {dy}{dx}}=e^{x}}
d
y
d
x
d
x
d
y
=
e
x
1
e
x
=
1
{\displaystyle {\frac {dy}{dx}}{\frac {dx}{dy}}=e^{x}{\frac {1}{e^{x}}}=1}
Finally,
A ·B = B ·A = I
Consider
[
A
]
N
{\displaystyle [\mathbf {A} ]_{N}}
N
=
2
p
{\displaystyle N=2p}
[
A
]
N
=
[
A
0
A
1
A
1
A
0
]
,
{\displaystyle [\mathbf {A} ]_{N}=\left[{\begin{array}{rrrr}\mathbf {A} _{0}&\mathbf {A} _{1}\\\mathbf {A} _{1}&\mathbf {A} _{0}\\\end{array}}\right],}
If
[
A
0
]
p
{\displaystyle [\mathbf {A} _{0}]_{p}}
[
A
1
]
p
{\displaystyle [\mathbf {A} _{1}]_{p}}
[
A
]
N
{\displaystyle [A]_{N}}
A
0
A
1
r
t
+
A
1
r
t
A
0
{\displaystyle \mathbf {A} _{0}\mathbf {A} _{1}^{rt}+\mathbf {A} _{1}^{rt}\mathbf {A} _{0}}
Let
A
0
=
[
−
1
1
1
1
]
,
{\displaystyle \mathbf {A} _{0}=\left[{\begin{array}{rrrr}-1&1\\1&1\\\end{array}}\right],}
A
1
=
[
−
1
−
1
−
1
1
]
,
{\displaystyle \mathbf {A} _{1}=\left[{\begin{array}{rrrr}-1&-1\\-1&1\\\end{array}}\right],}
[
A
]
N
{\displaystyle [\mathbf {A} ]_{N}}
[
A
]
4
=
[
A
0
A
1
A
0
A
1
]
=
[
−
1
1
−
1
−
1
1
1
−
1
1
−
1
1
−
1
−
1
1
1
−
1
1
]
,
{\displaystyle [\mathbf {A} ]_{4}=\left[{\begin{array}{rrrr}\mathbf {A} _{0}&\mathbf {A} _{1}\\\mathbf {A} _{0}&\mathbf {A} _{1}\\\end{array}}\right]=\left[{\begin{array}{rrrr}-1&1&-1&-1\\1&1&-1&1\\-1&1&-1&-1\\1&1&-1&1\\\end{array}}\right],}
[
A
]
4
{\displaystyle [\mathbf {A} ]_{4}}
[
U
C
A
G
]
T
⊗
[
U
C
A
G
]
⊗
[
U
C
A
G
]
T
,
{\displaystyle \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]^{T}\otimes \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]\otimes \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]^{T},}
where U , C , A , G denotes the amount of the DNA nucleobases and the matrix
[
A
]
4
{\displaystyle [\mathbf {A} ]_{4}}
[1] Moon Ho Lee, "The Center Weighted Hadamard Transform", IEEE Transactions on Circuits Syst. Vol. 36, No. 9, PP. 1247–1249, Sept. 1989.
[2] Kathy Horadam, Hadamard Matrices and Their Applications , Princeton University Press, UK, Chapter 4.5.1: The jacket matrix construction, PP. 85–91, 2007.
[3] Moon Ho Lee, Jacket Matrices: Constructions and Its Applications for Fast Cooperative Wireless Signal Processing , LAP LAMBERT Publishing, Germany, Nov. 2012.
[4] Moon Ho Lee, et. al., "MIMO Communication Method and System using the Block Circulant Jacket Matrix," US patent, no. US 009356671B1, May, 2016.
[5] S. K. Lee and M. H. Lee, “The COVID-19 DNA-RNA Genetic Code Analysis Using Information Theory of Double Stochastic Matrix,” IntechOpen, Book Chapter, April 17, 2022. [Available in Online: https://www.intechopen.com/chapters/81329 ].









![{\displaystyle A=\left[{\begin{array}{rrrr}1&1&1&1\\1&-2&2&-1\\1&2&-2&-1\\1&-1&-1&1\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0db861b6f4bf217242d96d618704deb3b87ef19)
![{\displaystyle B={1 \over 4}\left[{\begin{array}{rrrr}1&1&1&1\\[6pt]1&-{1 \over 2}&{1 \over 2}&-1\\[6pt]1&{1 \over 2}&-{1 \over 2}&-1\\[6pt]1&-1&-1&1\\[6pt]\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a8cc637797577e763b4f3b81e90622673039c40)
![{\displaystyle A=\left[{\begin{array}{rrrr}a&b&b&a\\b&-c&c&-b\\b&c&-c&-b\\a&-b&-b&a\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3686796010048b122d0688b008386a6abfd7de65)
![{\displaystyle B={1 \over 4}\left[{\begin{array}{rrrr}{1 \over a}&{1 \over b}&{1 \over b}&{1 \over a}\\[6pt]{1 \over b}&-{1 \over c}&{1 \over c}&-{1 \over b}\\[6pt]{1 \over b}&{1 \over c}&-{1 \over c}&-{1 \over b}\\[6pt]{1 \over a}&-{1 \over b}&-{1 \over b}&{1 \over a}\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f6ec5287dc89fda4acd0c8f0f37cd1472fd08d1)


![{\displaystyle J_{4}=\left[{\begin{array}{rrrr}I_{2}&0&0&0\\0&\cos \theta &-\sin \theta &0\\0&\sin \theta &\cos \theta &0\\0&0&0&I_{2}\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f98a1705edcf4b9200d359ce4a252e471501e052)








![{\displaystyle [\mathbf {A} ]_{N}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8782b7f4e3bfc201bc5c17a674add6f7317b236c)

![{\displaystyle [\mathbf {A} ]_{N}=\left[{\begin{array}{rrrr}\mathbf {A} _{0}&\mathbf {A} _{1}\\\mathbf {A} _{1}&\mathbf {A} _{0}\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab1b08b44b5940b158e5157c7118bb2018f1ee01)
![{\displaystyle [\mathbf {A} _{0}]_{p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/921e931d46cbaec47fd375218a96bdfc37e8fedc)
![{\displaystyle [\mathbf {A} _{1}]_{p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/191d29c940d6cfb2e358796d03a66f8d381cb1ef)
![{\displaystyle [A]_{N}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b142b1e0b12237f9b25bddb4780fc5d7432e48f2)

![{\displaystyle \mathbf {A} _{0}=\left[{\begin{array}{rrrr}-1&1\\1&1\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51839ea2c0784ebe94aa62c66893eeb715314b61)
![{\displaystyle \mathbf {A} _{1}=\left[{\begin{array}{rrrr}-1&-1\\-1&1\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03a6d490e468243824e2e82d097954d52a10d542)
![{\displaystyle [\mathbf {A} ]_{4}=\left[{\begin{array}{rrrr}\mathbf {A} _{0}&\mathbf {A} _{1}\\\mathbf {A} _{0}&\mathbf {A} _{1}\\\end{array}}\right]=\left[{\begin{array}{rrrr}-1&1&-1&-1\\1&1&-1&1\\-1&1&-1&-1\\1&1&-1&1\\\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b75efb84da10b64b207404a97a05b7102618469)
![{\displaystyle [\mathbf {A} ]_{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43981f84b7a48dc44bfc6c2826c079fa7b52f430)
![{\displaystyle \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]^{T}\otimes \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]\otimes \left[{\begin{array}{rrrr}U&C&A&G\\\end{array}}\right]^{T},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f6f0df5aa889845012a0cfcb0d51b2466924d11)