Guillotine partition: Difference between revisions
Erel Segal (talk | contribs) ←Redirected page to Guillotine cutting Tags: New redirect Visual edit |
Erel Segal (talk | contribs) Move some material from guillotine cutting Tags: Removed redirect nowiki added Visual edit |
||
| Line 1: | Line 1: | ||
[[File:CuttingStockGuillotine.png|link=https://en.wikipedia.org/wiki/File:CuttingStockGuillotine.png|thumb|A guillotine cutting: an optimised sheet of smaller rectangles which can be divided intact through the correct series of bisecting end-to-end cuts.]] |
|||
#REDIRECT [[Guillotine cutting]] |
|||
[[File:CuttingStockNonGuillotine.png|link=https://en.wikipedia.org/wiki/File:CuttingStockNonGuillotine.png|thumb|A non-guillotine cutting: these rectangles ''cannot'' be separated by making single bisecting cuts across the plane.]] |
|||
'''Guillotine partition''' is the process of partitioning a [[rectilinear polygon]], possibly containing some holes, into rectangles, using only guillotine-cuts. A '''guillotine-cut''' (also called an '''edge-to-edge cut''') is a straight bisecting line going from one edge of an existing polygon to the opposite edge, similarly to a [[paper guillotine]]. |
|||
Guillotine partition is particularly common in designing [[Floorplan (microelectronics)|floorplans in microelectronics]]. An alternative term for a guillotine-partition in this context is a '''slicing partition''' or a '''slicing floorplan'''.<ref>{{Citation|last=Lengauer|first=Thomas|title=Circuit Partitioning|date=1990|url=http://dx.doi.org/10.1007/978-3-322-92106-2_6|work=Combinatorial Algorithms for Integrated Circuit Layout|pages=251–301|place=Wiesbaden|publisher=Vieweg+Teubner Verlag|isbn=978-3-322-92108-6|access-date=2021-01-16}}</ref> Guillotine partitions are also the underlying structuer of [[Binary space partitioning|binary space partition]]<nowiki/>s. There are various [[optimization problem]]<nowiki/>s related to guillotine partition, such as: minimizing the number of rectangles or the total length of cuts. |
|||
A related but different problem is [[Guillotine cutting|''guillotine cutting'']]. In that problem, the original sheet is a plain rectangle without holes. The challenge comes from the fact that the dimensions of the small rectangles are fixed in advance. The optimization goals are usually to maximize the area of the produced rectangles or their value, or minimize the waste or the number of required sheets. |
|||
== Computing a guillotine partition with a smallest edge-length == |
|||
These are variants of [[Polygon partition|polygon partitioning]] problems, where the cuts are constrained to be guillotine cuts. Here, the input is a rectangle containing a set of points (or, more generally, holes), and the goal is to find a guillotine partition of the rectangle such that each cut passes through a single point, and the total edge length is minimal. |
|||
Without the restriction to guillotine cuts, the problem is NP-hard.<ref name=":6">{{Cite journal|last=Gonzalez|first=Teofilo F.|last2=Razzazi|first2=Mohammadreza|last3=Shing|first3=Man-Tak|last4=Zheng|first4=Si-Qing|date=1994-05-01|title=On optimal guillotine partitions approximating optimal d-box partitions|url=http://www.sciencedirect.com/science/article/pii/0925772194900132|journal=Computational Geometry|language=en|volume=4|issue=1|pages=1–11|doi=10.1016/0925-7721(94)90013-2|issn=0925-7721}}</ref> However, when restricted to guillotine cuts, a guillotine-partition with minimum edge-length can be found in time <math>O(n^5)</math>. Moreover, the edge-length in the optimal guillotine partition is at most 1.75 times in the optimal non-guillotine partition (it is not known if the 1.75 is tight, but there is an instance in which the approximation factor is 1.5).<ref>{{Cite journal|last=Gonzalez|first=Teofilo|last2=Zheng|first2=Si-Qing|date=1989-06-01|title=Improved bounds for rectangular and guillotine partitions|url=http://www.sciencedirect.com/science/article/pii/S0747717189800422|journal=Journal of Symbolic Computation|language=en|volume=7|issue=6|pages=591–610|doi=10.1016/S0747-7171(89)80042-2|issn=0747-7171}}</ref> Other approximation algorithms are known.<ref>{{Cite journal|last=Gonzalez|first=Teofilo|last2=Zheng|first2=Si-Qing|date=1985-06-01|title=Bounds for partitioning rectilinear polygons|url=https://doi.org/10.1145/323233.323269|journal=Proceedings of the first annual symposium on Computational geometry|series=SCG '85|location=Baltimore, Maryland, USA|publisher=Association for Computing Machinery|pages=281–287|doi=10.1145/323233.323269|isbn=978-0-89791-163-4}}</ref><ref>{{Cite journal|last=Gonzalez|first=Teofilo F.|last2=Razzazi|first2=Mohammadreza|last3=Zheng|first3=Si-Qing|date=1993-12-01|title=An efficient divide-and-conquer approximation algorithm for partitioning into d-boxes|url=https://www.worldscientific.com/doi/abs/10.1142/S0218195993000269|journal=International Journal of Computational Geometry & Applications|volume=03|issue=04|pages=417–428|doi=10.1142/S0218195993000269|issn=0218-1959}}</ref> |
|||
These results can be extended to a ''d''-dimensional box: a guillotine-partition with minimum edge-length can be found in time <math>O(d n^{2 d + 1})</math>, and the total (''d''-1)-volume in the optimal guillotine-partition is at most <math>2d-4+4/d</math> times that of an optimal ''d''-box partition.<ref name=":6" /> |
|||
== Number of guillotine partitions == |
|||
Besides the computational problems, guillotine partitions were also studied from a combinatorial perspective. Suppose a given rectangle should be partitioned into smaller rectangles using guillotine cuts only. Obviously, there are infinitely many ways to do this, since even a single cut can take infinitely many values. However, the number of ''structurally-different'' guillotine partitions is bounded. |
|||
* In two dimensions, there is an upper bound in <math>O\left ( \frac{ n! 2^{5n-3}}{n^{3/2}} \right)</math> attributed to [[Donald Knuth|Knuth]]. the exact number is the [[Schröder number]]. <ref>{{Cite journal|last=Yao|first=Bo|last2=Chen|first2=Hongyu|last3=Cheng|first3=Chung-Kuan|last4=Graham|first4=Ronald|date=2003-01-01|title=Floorplan representations: Complexity and connections|url=https://doi.org/10.1145/606603.606607|journal=ACM Transactions on Design Automation of Electronic Systems|volume=8|issue=1|pages=55–80|doi=10.1145/606603.606607|issn=1084-4309}}</ref> |
|||
* |
|||
* In ''d'' dimensions, Ackerman, Barequet, Pinter and Romik<ref>{{Cite journal|last=Ackerman|first=Eyal|last2=Barequet|first2=Gill|last3=Pinter|first3=Ron Y.|last4=Romik|first4=Dan|date=2006-05-31|title=The number of guillotine partitions in d dimensions|url=http://www.sciencedirect.com/science/article/pii/S0020019006000305|journal=Information Processing Letters|language=en|volume=98|issue=4|pages=162–167|doi=10.1016/j.ipl.2006.01.011|issn=0020-0190}}</ref> give an exact summation formula, and prove that it is in <math>\Theta\left (\frac{ (2 d - 1 + 2 \sqrt{d(d-1)})^n}{n^{3/2}} \right)</math>. When ''d''=2 this bound becomes <math>\Theta\left (\frac{ (3 + 2 \sqrt{2})^n}{n^{3/2}} \right)</math> |
|||
== See also == |
|||
* [[Binary space partitioning]] |
|||
== References == |
|||
<references group="" responsive="1"></references> |
|||
Revision as of 12:12, 17 January 2021

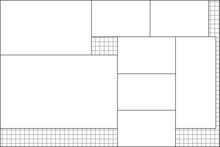
Guillotine partition is the process of partitioning a rectilinear polygon, possibly containing some holes, into rectangles, using only guillotine-cuts. A guillotine-cut (also called an edge-to-edge cut) is a straight bisecting line going from one edge of an existing polygon to the opposite edge, similarly to a paper guillotine.
Guillotine partition is particularly common in designing floorplans in microelectronics. An alternative term for a guillotine-partition in this context is a slicing partition or a slicing floorplan.[1] Guillotine partitions are also the underlying structuer of binary space partitions. There are various optimization problems related to guillotine partition, such as: minimizing the number of rectangles or the total length of cuts.
A related but different problem is guillotine cutting. In that problem, the original sheet is a plain rectangle without holes. The challenge comes from the fact that the dimensions of the small rectangles are fixed in advance. The optimization goals are usually to maximize the area of the produced rectangles or their value, or minimize the waste or the number of required sheets.
Computing a guillotine partition with a smallest edge-length
These are variants of polygon partitioning problems, where the cuts are constrained to be guillotine cuts. Here, the input is a rectangle containing a set of points (or, more generally, holes), and the goal is to find a guillotine partition of the rectangle such that each cut passes through a single point, and the total edge length is minimal.
Without the restriction to guillotine cuts, the problem is NP-hard.[2] However, when restricted to guillotine cuts, a guillotine-partition with minimum edge-length can be found in time . Moreover, the edge-length in the optimal guillotine partition is at most 1.75 times in the optimal non-guillotine partition (it is not known if the 1.75 is tight, but there is an instance in which the approximation factor is 1.5).[3] Other approximation algorithms are known.[4][5]
These results can be extended to a d-dimensional box: a guillotine-partition with minimum edge-length can be found in time , and the total (d-1)-volume in the optimal guillotine-partition is at most times that of an optimal d-box partition.[2]
Number of guillotine partitions
Besides the computational problems, guillotine partitions were also studied from a combinatorial perspective. Suppose a given rectangle should be partitioned into smaller rectangles using guillotine cuts only. Obviously, there are infinitely many ways to do this, since even a single cut can take infinitely many values. However, the number of structurally-different guillotine partitions is bounded.
- In two dimensions, there is an upper bound in attributed to Knuth. the exact number is the Schröder number. [6]
- In d dimensions, Ackerman, Barequet, Pinter and Romik[7] give an exact summation formula, and prove that it is in . When d=2 this bound becomes
See also
References
- ^ Lengauer, Thomas (1990), "Circuit Partitioning", Combinatorial Algorithms for Integrated Circuit Layout, Wiesbaden: Vieweg+Teubner Verlag, pp. 251–301, ISBN 978-3-322-92108-6, retrieved 2021-01-16
- ^ a b Gonzalez, Teofilo F.; Razzazi, Mohammadreza; Shing, Man-Tak; Zheng, Si-Qing (1994-05-01). "On optimal guillotine partitions approximating optimal d-box partitions". Computational Geometry. 4 (1): 1–11. doi:10.1016/0925-7721(94)90013-2. ISSN 0925-7721.
- ^ Gonzalez, Teofilo; Zheng, Si-Qing (1989-06-01). "Improved bounds for rectangular and guillotine partitions". Journal of Symbolic Computation. 7 (6): 591–610. doi:10.1016/S0747-7171(89)80042-2. ISSN 0747-7171.
- ^ Gonzalez, Teofilo; Zheng, Si-Qing (1985-06-01). "Bounds for partitioning rectilinear polygons". Proceedings of the first annual symposium on Computational geometry. SCG '85. Baltimore, Maryland, USA: Association for Computing Machinery: 281–287. doi:10.1145/323233.323269. ISBN 978-0-89791-163-4.
- ^ Gonzalez, Teofilo F.; Razzazi, Mohammadreza; Zheng, Si-Qing (1993-12-01). "An efficient divide-and-conquer approximation algorithm for partitioning into d-boxes". International Journal of Computational Geometry & Applications. 03 (04): 417–428. doi:10.1142/S0218195993000269. ISSN 0218-1959.
- ^ Yao, Bo; Chen, Hongyu; Cheng, Chung-Kuan; Graham, Ronald (2003-01-01). "Floorplan representations: Complexity and connections". ACM Transactions on Design Automation of Electronic Systems. 8 (1): 55–80. doi:10.1145/606603.606607. ISSN 1084-4309.
- ^ Ackerman, Eyal; Barequet, Gill; Pinter, Ron Y.; Romik, Dan (2006-05-31). "The number of guillotine partitions in d dimensions". Information Processing Letters. 98 (4): 162–167. doi:10.1016/j.ipl.2006.01.011. ISSN 0020-0190.






