On the Equilibrium of Planes: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
Added more details.
Added new citations to match.
Line 53: Line 53:


== Legacy ==
== Legacy ==
Archimedes' mechanical works, including ''On the Equilibrium of Planes'', were well known but little read in antiquity. Both [[Hero of Alexandria|Hero]] and [[Pappus of Alexandria|Pappus]] quote Archimedes extensively in their work on mechanics, particularly with regards to the centre of gravity and the law of the lever. [[Vitruvius]] appears to have some knowledge of the work as well.
Archimedes' mechanical works, including ''On the Equilibrium of Planes'', were well known but little read in antiquity. Both [[Hero of Alexandria|Hero]] and [[Pappus of Alexandria|Pappus]] quote Archimedes extensively in their work on mechanics, particularly with regards to the centre of gravity and the law of the lever. [[Vitruvius]] appears to have some knowledge of the work as well.<ref>{{Cite journal |last=Drachmann |first=A. G. |date=1968 |title=Archimedes and the Science of Physics |url=https://onlinelibrary.wiley.com/doi/10.1111/j.1600-0498.1968.tb00074.x |journal=Centaurus |language=en |volume=12 |issue=1 |pages=1–11 |doi=10.1111/j.1600-0498.1968.tb00074.x |issn=0008-8994}}</ref><ref>{{Cite book |last=Assis |first=A.K.T. |title=Archimedes, the Center of Gravity, and the First Law of Mechanics |publisher=C. Roy Keys Incorporated |year=2010 |isbn=9780986492648 |edition=2nd}}</ref>


In the Middle Ages, Arabic authors were familiar with and extended Archimedes' work on balances and centre of gravity; in the Latin West, however, these ideas were virtually unknown except for a handful of limited cases. It is only in the [[Science in the Renaissance|Renaissance]] that the results found in ''On the Equilibrium of Planes'' began to spread widely. Archimedes' mathematical approach to physics, in particular, became a model for subsequent scientists such as [[Guidobaldo del Monte]], [[Bernardino Baldi]], [[Simon Stevin]], and [[Galileo Galilei]].
In the Middle Ages, Arabic authors were familiar with and extended Archimedes' work on balances and centre of gravity; in the Latin West, however, these ideas were virtually unknown except for a handful of limited cases.<ref>{{Cite journal |last=Clagett |first=M. |date=1959 |title=The Impact of Archimedes on Medieval Science |url=https://www.jstor.org/stable/226426 |journal=Isis |volume=50 |issue=4 |pages=419–429 |issn=0021-1753}}</ref><ref>{{Citation |last=Høyrup |first=J. |title=Archimedes – Knowledge and Lore from Latin Antiquity to the Outgoing European Renaissance |date=2019 |url=https://doi.org/10.1007/978-3-030-19258-7_17 |work=Selected Essays on Pre- and Early Modern Mathematical Practice |pages=459–477 |editor-last=Høyrup |editor-first=J. |place=Cham |publisher=Springer International Publishing |language=en |doi=10.1007/978-3-030-19258-7_17 |isbn=978-3-030-19258-7 |access-date=}}</ref> It is only in the [[Science in the Renaissance|Renaissance]] that the results found in ''On the Equilibrium of Planes'' began to spread widely. Archimedes' mathematical approach to physics, in particular, became a model for subsequent scientists such as [[Guidobaldo del Monte]], [[Bernardino Baldi]], [[Simon Stevin]], and [[Galileo Galilei]].<ref>{{Cite journal |last=Palmieri |first=P. |date=2008 |title=Breaking the circle: the emergence of Archimedean mechanics in the late Renaissance |url=https://doi.org/10.1007/s00407-007-0012-8 |journal=Archive for History of Exact Sciences |language=en |volume=62 |issue=3 |pages=301–346 |doi=10.1007/s00407-007-0012-8 |issn=1432-0657}}</ref><ref>{{Cite book |last=Meli |first=D. |url=https://books.google.com/books?hl=en&lr=&id=ar7RK8xtJgYC&oi=fnd&pg=PA23&dq=axiomatic+tradition+seventeenth+century&ots=m8W4QkKJas&sig=5Iur0GRJM2uY89ATipOH9Q0-Sro#v=onepage&q=axiomatic%20tradition%20seventeenth%20century&f=false |title=Discourse on a New Method: Reinvigorating the Marriage of History and Philosophy of Science |date=2010 |publisher= |isbn=978-0-8126-9662-2 |pages=23-41 |language=en |chapter=The axiomatic tradition in seventeenth-century mechanics}}</ref>


In the second half of the [[Scientific Revolution|seventeenth century]], the concept of centre of gravity reached a high level of sophistication and was pivotal in the development of rational mechanics, as shown for instance in the works of [[Evangelista Torricelli]] and [[Christiaan Huygens]].
In the second half of the [[Scientific Revolution|seventeenth century]], the concept of centre of gravity reached a high level of sophistication and was pivotal in the development of rational mechanics, as shown for instance in the works of [[Evangelista Torricelli]] and [[Christiaan Huygens]].<ref>{{Cite journal |last=Pisano |first=R. |last2=Bussotti |first2=P. |last3=Bussotti |first3=Paolo |last4=Bussotti |first4=Paolo |date=2014 |title=Notes on mechanics and mathematics in Torricelli as physics mathematics relationships in the history of science. |url=http://www.scientiasocialis.lt/pec/node/922 |journal=Problems of Education in the 21st Century |volume=61 |pages=Discontinuous |doi=10.33225/pec/14.61.88 |issn=1822-7864}}</ref><ref>{{Citation |last=Van Dyck |first=M. |title=Mechanical philosophy : science of mechanics |date=2020 |url=http://hdl.handle.net/1854/LU-8678741 |work=Encyclopedia of early modern philosophy and the sciences |pages=1–11 |publisher=Springer |isbn=978-3-319-20791-9 |access-date=}}</ref>


=== Criticism ===
=== Criticism ===

Revision as of 19:11, 12 July 2022

On the Equilibrium of Planes I-II
AuthorArchimedes
LanguageDoric Greek
GenrePhysics, Geometry

On the Equilibrium of Planes (Ancient Greek: Περὶ ἐπιπέδων ἱσορροπιῶν, romanized: perí epípedon isorropión) is a treatise by Archimedes in two volumes. The first book contains a proof of the law of the lever and culminates with propositions on the centre of gravity of the triangle and the trapezium.[1][2] The second book, which contains ten propositions, examines the centres of gravity of parabolic segments.[1]

According to Pappus of Alexandria, Archimedes' work on levers caused him to say: "Give me a place to stand on, and I will move the Earth" (Ancient Greek: δός μοί ποῦ στῶ καὶ κινῶ τὴν γῆν, romanized: dṓs moi poû stṓ kaí kinô tḗn gên), though other ancient testimonia are ambiguous regarding the context of the saying.[3][4]

Overview

The lever and its properties were already well known before the time of Archimedes, and he was not the first to provide an analysis of the principle of the lever.[5] The earlier Mechanical Problems, once attributed to Aristotle but most likely written by one of his successors, contains a loose proof of the law without employing the concept of centre of gravity. There is another short work attributed to Euclid entitled On the Balance that also contains a mathematical proof of the law of the lever, again without recourse to the centre of gravity.[6]

In contrast, in Archimedes' work the concept of centre of gravity is central.[7] On the Equilibrium of Planes I, which contains seven postulates and fifteen propositions, uses the centre of gravity for both commensurable and incommensurable magnitudes to justify the law of the lever, though some argue not satisfactorily.[2] Archimedes then proceeds to locate the centre of gravity of the parallelogram and the triangle, ending book one with a proof on the centre of gravity of the trapezium.

On the Equilibrium of Planes II shares the same subject area as the first book but was written at a later date. It contains ten propositions regarding the centre of gravity of parabolic segments exclusively, examining these segments by substituting them with rectangles of equal area. This exchange was made possible by results obtained in Quadrature of the Parabola, a treatise believed to have been published after book one of On the Equilibrium of Planes.[1][2]

Contents

Book one

The first half of book one deals with the properties of the balance and the law of the lever, while the second half focuses on the centre of gravity of basic plane figures. The law makes use in particular of the first postulate, which states that "equal weights at equal distances are in equilibrium". In Propositions 4 and 5, Archimedes expands this observation to include the concept of the centre of gravity: he proves that the centre of gravity of any system consisting of an even number of equal weights, equally distributed, will be located at the midpoint between the two centre weights. Archimedes then uses these theorems to prove the law of the lever in Proposition 6 (for commensurate cases) and Proposition 7 (for incommensurate cases).

Weights and levers at a ratio of four to three.

Law of the lever

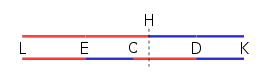
Given two unequal, but commensurable, weights and a lever arm divided into two unequal, yet commensurable, portions (see sketch opposite), if the magnitudes A and B are applied at points E and D, respectively, the system will be in equilibrium if the weights are inversely proportional to the lengths:

Let us assume that lines and weights are constructed to obey the rule using a common measure (or unit) N, and at a ratio of four to three (as per the sketch). Now, double the length of ED by duplicating the longer arm on the left, and the shorter arm on the right.

For demonstration's sake, reorder the lines so that CD is adjacent to LE (the two red lines together), and juxtapose with the original (as below):

It is clear then, that both lines are double the length of the original line ED, that LH has its centre at E, and HK its centre at D. Note, additionally, that EH (which is equal to CD) carries the common measure (or unit) N, an exact number of times, as does EC, and therefore, by inference, CH too. It remains then to prove that A applied at E, and B applied at D, will have their centre of gravity at C.

Therefore, as the ratio of LH to HK has doubled the original distances EC and ED, similarly divide the magnitudes A and B into a ratio of eight to six (a transformation that conserves their original ratio of four to three), and align them so that the A units (red) are centred on E, while the B units (blue) are centred on D.

Now, since an even number of equal weights, equally spaced, have their centre of gravity between the two middle weights, A is in fact applied at E, and B at D, as the proposition requires. Further, the total system consists of an even number of equal weights equally distributed, and, therefore, following the same law, C must be the centre of gravity of the full system. Thus, it follows that as A is to B, so is CD to EC, and the system does not incline but is in equilibrium.[1]

Book two

The main objective of book two of On the Equilibrium of Planes is the determination of the centre of gravity of any part of a parabolic segment, shown in Proposition 8.

The book begins with a simpler proof of the law of the lever in Proposition 1, making reference to results found in Quadrature of the Parabola. Archimedes then proves the next seven propositions by combining the concept of centre of gravity and the properties of the parabola dealt with in book one of On the Equilibrium of Planes. More importantly, he infers that two parabolas equal in area have their centre of gravity equidistant from some point, and later substitutes their areas with rectangles of equal area.[1]

The last two propositions, Propositions 9 and 10, are rather obtuse but focus on the determination of the centre of gravity of a figure cut off from any parabolic segment by a frustum.[8]

Legacy

Archimedes' mechanical works, including On the Equilibrium of Planes, were well known but little read in antiquity. Both Hero and Pappus quote Archimedes extensively in their work on mechanics, particularly with regards to the centre of gravity and the law of the lever. Vitruvius appears to have some knowledge of the work as well.[9][10]

In the Middle Ages, Arabic authors were familiar with and extended Archimedes' work on balances and centre of gravity; in the Latin West, however, these ideas were virtually unknown except for a handful of limited cases.[11][12] It is only in the Renaissance that the results found in On the Equilibrium of Planes began to spread widely. Archimedes' mathematical approach to physics, in particular, became a model for subsequent scientists such as Guidobaldo del Monte, Bernardino Baldi, Simon Stevin, and Galileo Galilei.[13][14]

In the second half of the seventeenth century, the concept of centre of gravity reached a high level of sophistication and was pivotal in the development of rational mechanics, as shown for instance in the works of Evangelista Torricelli and Christiaan Huygens.[15][16]

Criticism

A number of researches have highlighted inconsistencies within the first book of On the Equilibrium of Planes.[2][8][17] Berggren questions the validity of much of book one, noting for instance the redundancy of Propositions 1-3 and 11-12. However, he follows Dijksterhuis in rejecting Mach's criticism of Proposition 6 and highlighting instead its significance, mainly "if a system of weights suspended on a balance beam is in equilibrium when supported at a particular point, then any redistribution of these weights, that preserves their common centre of gravity, also preserves the equilibrium."[2][8]

Proposition 7 of book one appears incomplete in its current form, so that strictly speaking Archimedes in the first book demonstrates the law of the lever for commensurable magnitudes only.[1][2] The second book of On the Equilibrium of Planes does not suffer from these issues because, with the exception of the first proposition, the lever is not treated at all.[8] Perhaps more concerning is that there is no definition of centre of gravity anywhere in Archimedes' extant works, make it difficult to see the logical structure of some of his arguments in On the Equilibrium of Planes.[5][7]

References

  1. ^ a b c d e f Heath, T.L. (1897). "The Works of Archimedes (1897). The unabridged work in PDF form (19 MB)". Cambridge University Press. Archived from the original on 6 October 2007. Retrieved 2013-01-06.
  2. ^ a b c d e f John Lennart Berggren (1976). "Spurious Theorems in Archimedes' Equilibrium of Planes Book I". Archive for History of Exact Sciences (Internet). Archive for History of Exact Sciences 16(2), 87-103. ISSN 1432-0657.
  3. ^ Quoted by Pappus of Alexandria in Synagoge, Book VIII, p. 1060 in ed. Hultsch
  4. ^ Berryman, S. (2020). "How Archimedes Proposed to Move the Earth". Isis. 111 (3): 562–567. doi:10.1086/710317. ISSN 0021-1753. S2CID 224841008.
  5. ^ a b Goe, G. (1972). "Archimedes' theory of the lever and Mach's critique". Studies in History and Philosophy of Science Part A. 2 (4): 329–345. doi:10.1016/0039-3681(72)90002-7. ISSN 0039-3681.
  6. ^ Renn, J., Damerow, P., & McLaughlin, P. (2003). Aristotle, Archimedes, Euclid, and the origin of mechanics: The perspective of historical epistemology. In J. L. Montesinos Sirera (Ed.), Symposium Arquímedes Fundación Canaria Orotava de Historia de la Ciencia (pp. 43–59). http://www.mpiwg-berlin.mpg.de/Preprints/P239.PDF.
  7. ^ a b Magnaghi, C. P.; Assis, A. K. T. (2012-05-07). "Calculation of the centre of gravity of the cone utilizing the method of Archimedes". European Journal of Physics. 33 (3): 637–646. doi:10.1088/0143-0807/33/3/637. ISSN 0143-0807.
  8. ^ a b c d Dijksterhuis, E.J. (1987). Archimedes. Princeton University Press, Princeton. ISBN 0-691-08421-1. Republished translation of the 1938 study of Archimedes and his works by an historian of science.
  9. ^ Drachmann, A. G. (1968). "Archimedes and the Science of Physics". Centaurus. 12 (1): 1–11. doi:10.1111/j.1600-0498.1968.tb00074.x. ISSN 0008-8994.
  10. ^ Assis, A.K.T. (2010). Archimedes, the Center of Gravity, and the First Law of Mechanics (2nd ed.). C. Roy Keys Incorporated. ISBN 9780986492648.
  11. ^ Clagett, M. (1959). "The Impact of Archimedes on Medieval Science". Isis. 50 (4): 419–429. ISSN 0021-1753.
  12. ^ Høyrup, J. (2019), Høyrup, J. (ed.), "Archimedes – Knowledge and Lore from Latin Antiquity to the Outgoing European Renaissance", Selected Essays on Pre- and Early Modern Mathematical Practice, Cham: Springer International Publishing, pp. 459–477, doi:10.1007/978-3-030-19258-7_17, ISBN 978-3-030-19258-7
  13. ^ Palmieri, P. (2008). "Breaking the circle: the emergence of Archimedean mechanics in the late Renaissance". Archive for History of Exact Sciences. 62 (3): 301–346. doi:10.1007/s00407-007-0012-8. ISSN 1432-0657.
  14. ^ Meli, D. (2010). "The axiomatic tradition in seventeenth-century mechanics". Discourse on a New Method: Reinvigorating the Marriage of History and Philosophy of Science. pp. 23–41. ISBN 978-0-8126-9662-2.
  15. ^ Pisano, R.; Bussotti, P.; Bussotti, Paolo; Bussotti, Paolo (2014). "Notes on mechanics and mathematics in Torricelli as physics mathematics relationships in the history of science". Problems of Education in the 21st Century. 61: Discontinuous. doi:10.33225/pec/14.61.88. ISSN 1822-7864.
  16. ^ Van Dyck, M. (2020), "Mechanical philosophy : science of mechanics", Encyclopedia of early modern philosophy and the sciences, Springer, pp. 1–11, ISBN 978-3-319-20791-9
  17. ^ Mach, E. (1907). The science of Mechanics a Critical and Historical Account of its Development. Open Court, Chicago. Republished translation of the 1883 original by Thomas J. McCormack. Ed. 3, rev.
Retrieved from "https://en.wikipedia.org/w/index.php?title=On_the_Equilibrium_of_Planes&oldid=1097813608"