Bisection

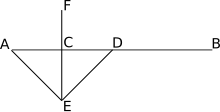
Line DE bisects line AB at D, line EF is a perpendicular bisector of segment AD at C, and line EF is the interior bisector of right angle AED

In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector (a line that passes through the midpoint of a given segment) and the angle bisector (a line that passes through the apex of an angle, that divides it into two equal angles).

In three dimensional space, bisection is usually done by a plane, also called the bisector or bisecting plane.

Line segment bisector

Bisection of a line segment using a compass and ruler

A line segment bisector passes through the midpoint of the segment. Particularly important is the perpendicular bisector of a segment, which, according to its name, meets the segment at right angles. The perpendicular bisector of a segment also has the property that each of its points is equidistant from the segment's endpoints. Therefore Voronoi diagram boundaries consist of segments of such lines or planes.

In classical geometry, the bisection is a simple compass and straightedge, whose possibility depends on the ability to draw circles of equal radii and different centers. The segment is bisected by drawing intersecting circles of equal radius, whose centers are the endpoints of the segment and such that each circle goes through one endpoint. The line determined by the points of intersection of the two circles is the perpendicular bisector of the segment, since it crosses the segment at its center. This construction is in fact used when constructing a line perpendicular to a given line at a given point: drawing an arbitrary circle whose center is that point, it intersects the line in two more points, and the perpendicular to be constructed is the one bisecting the segment defined by these two points.

Angle bisector

Bisection of an angle using a compass and ruler

An angle bisector divides the angle into two angles with equal measures. An angle only has one bisector. Each point of an angle bisector is equidistant from the sides of the angle.

The interior bisector of an angle is the half-line or line segment that divides an angle of less than 180° into two equal angles. The exterior bisector is the half-line that divides the opposite angle (of greater than 180°) into two equal angles.

To bisect an angle with straightedge and compass, one draws a circle whose center is the vertex. The circle meets the angle at two points: one on each leg. Using each of these points as a center, draw two circles of the same size. The intersection of the circles (two points) determines a line that is the angle bisector.

The proof of the correctness of these two constructions is fairly intuitive, relying on the symmetry of the problem. It is interesting to note that the trisection of an angle (dividing it into three equal parts) cannot be achieved with the ruler and compass alone (this was first proved by Pierre Wantzel).

Angle bisectors of a triangle

The angle bisectors of the angles of a triangle are concurrent in a point called the incenter of the triangle.

If the side lengths of a triangle are $a,b,c$ , the semiperimeter ( $(a+b+c)/2)$ ) is $s$ , and A is the angle opposite side $a$ , the length of the internal bisector of angle A is^[1]

{\frac {2{\sqrt {bcs(s-a)}}}{b+c}}

.

If the internal bisector of angle A in triangle ABC has length $t_{a}$ and if this bisector divides the side opposite A into segments of lengths m and n, then^[1]

t_{a}^{2}+mn=bc

where b and c are the side lengths opposite vertices B and C; and the side opposite A is divided in the proportion b:c.

If the internal bisectors of angles A, B, and C have lengths $t_{a},t_{b},$ and $t_{c}$ , then^[2]

{\frac {(b+c)^{2}}{bc}}t_{a}^{2}+{\frac {(c+a)^{2}}{ca}}t_{b}^{2}+{\frac {(a+b)^{2}}{ab}}t_{c}^{2}=(a+b+c)^{2}.

The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

No two non-congruent triangles share the same set of three internal angle bisector lengths.^[3]^[4]

Angle bisectors of a rhombus

Each diagonal of a rhombus bisects opposite angles.

Area bisectors and area-perimeter bisectors of a triangle

There are an infinitude of lines that bisect the area of a triangle. Three of them are the medians of the triangle (which connect the sides' midpoints with the opposite vertices), and these are concurrent at the triangle's centroid; indeed, they are the only area bisectors that go through the centroid. Three other area bisectors are parallel to the triangle's sides; each of these intersects the other two sides so as to divide them into segments with the proportions ${\sqrt {2}}+1:1$ .^[5] These six lines are concurrent three at a time: in addition to the three medians being concurrent, any one median is concurrent with two of the side-parallel area bisectors.

The envelope of the infinitude of area bisectors is a deltoid (broadly defined as a figure with three vertices connected by curves that are concave to the exterior of the deltoid, making the interior points a non-convex set).^[5] The vertices of the deltoid are at the midpoints of the medians; all points inside the deltoid are on three different area bisectors, while all points outside it are on just one. [1] The sides of the deltoid are arcs of hyperbolas that are asymptotic to the extended sides of the triangle.^[5]

Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle. A line through the incenter bisects one of the area or perimeter if and only if it also bisects the other.^[6]

Area and diagonal bisectors of a parallelogram

Any line through the midpoint of a parallelogram bisects the area.^[7] Also, the diagonals of a parallelogram bisect each other.

Angle bisector theorem

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

References

^ ^a ^b Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929), p. 70.
^ Simons, Stuart. Mathematical Gazette 93, March 2009, 115-116.
^ Mironescu, P., and Panaitopol, L., "The existence of a triangle with prescribed angle bisector lengths", American Mathematical Monthly 101 (1994): 58–60.
^ Oxman, Victor, "A purely geometric proof of the uniqueness of a triangle with prescribed angle bisectors", Forum Geometricorum 8 (2008): 197–200.
^ ^a ^b ^c Dunn, J. A., and Pretty, J. E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108.
^ Kodokostas, Dimitrios, "Triangle Equalizers," Mathematics Magazine 83, April 2010, pp. 141-146.
^ Dunn, J. A., and J. E. Pretty, "Halving a triangle", Mathematical Gazette 56, May 1972, p. 105.

External links

The Angle Bisector at cut-the-knot
Angle Bisector definition. Math Open Reference With interactive applet
Line Bisector definition. Math Open Reference With interactive applet
Perpendicular Line Bisector. With interactive applet
Animated instructions for bisecting an angle and bisecting a line Using a compass and straightedge
Weisstein, Eric W. "Line Bisector". MathWorld.

This article incorporates material from Angle bisector on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

[Johnson-1] Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929), p. 70.

[2] Simons, Stuart. Mathematical Gazette 93, March 2009, 115-116.

[3] Mironescu, P., and Panaitopol, L., "The existence of a triangle with prescribed angle bisector lengths", American Mathematical Monthly 101 (1994): 58–60.

[4] Oxman, Victor, "A purely geometric proof of the uniqueness of a triangle with prescribed angle bisectors", Forum Geometricorum 8 (2008): 197–200.

[Dunn-5] Dunn, J. A., and Pretty, J. E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108.

[6] Kodokostas, Dimitrios, "Triangle Equalizers," Mathematics Magazine 83, April 2010, pp. 141-146.

[7] Dunn, J. A., and J. E. Pretty, "Halving a triangle", Mathematical Gazette 56, May 1972, p. 105.

[1]

[2]

[3]

[4]

[5]

[6]

[7]