Dynamo theory

In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
History of theory[edit]
When William Gilbert published de Magnete in 1600, he concluded that the Earth is magnetic and proposed the first hypothesis for the origin of this magnetism: permanent magnetism such as that found in lodestone. In 1822, André-Marie Ampère proposed that internal currents are responsible for Earth magnetism [2] . In 1919, Joseph Larmor proposed that a dynamo might be generating the field.[3][4] However, even after he advanced his hypothesis, some prominent scientists advanced alternative explanations. The Nobel Prize winner Patrick Blackett did a series of experiments looking for a fundamental relation between angular momentum and magnetic moment, but found none.[5][6]
Walter M. Elsasser, considered a "father" of the presently accepted dynamo theory as an explanation of the Earth's magnetism, proposed that this magnetic field resulted from electric currents induced in the fluid outer core of the Earth. He revealed the history of the Earth's magnetic field through pioneering the study of the magnetic orientation of minerals in rocks.
In order to maintain the magnetic field against ohmic decay (which would occur for the dipole field in 20,000 years), the outer core must be convecting. The convection is likely some combination of thermal and compositional convection. The mantle controls the rate at which heat is extracted from the core. Heat sources include gravitational energy released by the compression of the core, gravitational energy released by the rejection of light elements (probably sulfur, oxygen, or silicon) at the inner core boundary as it grows, latent heat of crystallization at the inner core boundary, and radioactivity of potassium, uranium and thorium.[7]
At the dawn of the 21st century, numerical modeling of the Earth's magnetic field has not been successfully demonstrated. Initial models are focused on field generation by convection in the planet's fluid outer core. It was possible to show the generation of a strong, Earth-like field when the model assumed a uniform core-surface temperature and exceptionally high viscosities for the core fluid. Computations which incorporated more realistic parameter values yielded magnetic fields that were less Earth-like, but indicated that model refinements [which?] may ultimately lead to an accurate analytic model. Slight variations in the core-surface temperature, in the range of a few millikelvins, result in significant increases in convective flow and produce more realistic magnetic fields.[8][9]
Formal definition[edit]
Dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid acts to maintain a magnetic field. This theory is used to explain the presence of anomalously long-lived magnetic fields in astrophysical bodies. The conductive fluid in the geodynamo is liquid iron in the outer core, and in the solar dynamo is ionized gas at the tachocline. Dynamo theory of astrophysical bodies uses magnetohydrodynamic equations to investigate how the fluid can continuously regenerate the magnetic field.[10]
It was once believed that the dipole, which comprises much of the Earth's magnetic field and is misaligned along the rotation axis by 11.3 degrees, was caused by permanent magnetization of the materials in the earth. This means that dynamo theory was originally used to explain the Sun's magnetic field in its relationship with that of the Earth. However, this hypothesis, which was initially proposed by Joseph Larmor in 1919, has been modified due to extensive studies of magnetic secular variation, paleomagnetism (including polarity reversals), seismology, and the solar system's abundance of elements. Also, the application of the theories of Carl Friedrich Gauss to magnetic observations showed that Earth's magnetic field had an internal, rather than external, origin.
There are three requisites for a dynamo to operate:
- An electrically conductive fluid medium
- Kinetic energy provided by planetary rotation
- An internal energy source to drive convective motions within the fluid.[11]
In the case of the Earth, the magnetic field is induced and constantly maintained by the convection of liquid iron in the outer core. A requirement for the induction of field is a rotating fluid. Rotation in the outer core is supplied by the Coriolis effect caused by the rotation of the Earth. The Coriolis force tends to organize fluid motions and electric currents into columns (also see Taylor columns) aligned with the rotation axis. Induction or generation of magnetic field is described by the induction equation:
Tidal heating supporting a dynamo[edit]
Tidal forces between celestial orbiting bodies cause friction that heats up their interiors. This is known as tidal heating, and it helps keep the interior in a liquid state. A liquid interior that can conduct electricity is required to produce a dynamo. Saturn's Enceladus and Jupiter's Io have enough tidal heating to liquify their inner cores, but they may not create a dynamo because they cannot conduct electricity.[12][13] Mercury, despite its small size, has a magnetic field, because it has a conductive liquid core created by its iron composition and friction resulting from its highly elliptical orbit.[14] It is theorized that the Moon once had a magnetic field, based on evidence from magnetized lunar rocks, due to its short-lived closer distance to Earth creating tidal heating.[15] An orbit and rotation of a planet helps provide a liquid core, and supplements kinetic energy that supports a dynamo action.
Kinematic dynamo theory[edit]
In kinematic dynamo theory the velocity field is prescribed, instead of being a dynamic variable: The model makes no provision for the flow distorting in response to the magnetic field. This method cannot provide the time variable behaviour of a fully nonlinear chaotic dynamo, but can be used to study how magnetic field strength varies with the flow structure and speed.
Using Maxwell's equations simultaneously with the curl of Ohm's law, one can derive what is basically a linear eigenvalue equation for magnetic fields (B), which can be done when assuming that the magnetic field is independent from the velocity field. One arrives at a critical magnetic Reynolds number, above which the flow strength is sufficient to amplify the imposed magnetic field, and below which the magnetic field dissipates.
Practical measure of possible dynamos[edit]
The most functional feature of kinematic dynamo theory is that it can be used to test whether a velocity field is or is not capable of dynamo action. By experimentally applying a certain velocity field to a small magnetic field, one can observe whether the magnetic field tends to grow (or not) in response to the applied flow. If the magnetic field does grow, then the system is either capable of dynamo action or is a dynamo, but if the magnetic field does not grow, then it is simply referred to as “not a dynamo”.
An analogous method called the membrane paradigm is a way of looking at black holes that allows for the material near their surfaces to be expressed in the language of dynamo theory.
Spontaneous breakdown of a topological supersymmetry[edit]
Kinematic dynamo can be also viewed as the phenomenon of the spontaneous breakdown of the topological supersymmetry of the associated stochastic differential equation related to the flow of the background matter.[16] Within stochastic supersymmetric theory, this supersymmetry is an intrinsic property of all stochastic differential equations, its interpretation is that the model's phase space preserves continuity via continuous time flows. When the continuity of that flow spontaneously breaks down, the system is in the stochastic state of deterministic chaos.[17] In other words, kinematic dynamo arises because of chaotic flow in the underlying background matter.
Nonlinear dynamo theory[edit]
The kinematic approximation becomes invalid when the magnetic field becomes strong enough to affect the fluid motions. In that case the velocity field becomes affected by the Lorentz force, and so the induction equation is no longer linear in the magnetic field. In most cases this leads to a quenching of the amplitude of the dynamo. Such dynamos are sometimes also referred to as hydromagnetic dynamos.[18] Virtually all dynamos in astrophysics and geophysics are hydromagnetic dynamos.
The main idea of the theory is that any small magnetic field existing in the outer core creates currents in the moving fluid there due to Lorentz force. These currents create further magnetic field due to Ampere's law. With the fluid motion, the currents are carried in a way that the magnetic field gets stronger (as long as is negative[19]). Thus a "seed" magnetic field can get stronger and stronger until it reaches some value that is related to existing non-magnetic forces.
Numerical models are used to simulate fully nonlinear dynamos. The following equations are used:
- The induction equation, presented above.
- Maxwell's equations for negligible electric field:
- The continuity equation for conservation of mass, for which the Boussinesq approximation is often used:
- The Navier-Stokes equation for conservation of momentum, again in the same approximation, with the magnetic force and gravitation force as the external forces: where is the kinematic viscosity, is the mean density and is the relative density perturbation that provides buoyancy (for thermal convection where is coefficient of thermal expansion), is the rotation rate of the Earth, and is the electric current density.
- A transport equation, usually of heat (sometimes of light element concentration): where T is temperature, is the thermal diffusivity with k thermal conductivity, heat capacity, and density, and is an optional heat source. Often the pressure is the dynamic pressure, with the hydrostatic pressure and centripetal potential removed.
These equations are then non-dimensionalized, introducing the non-dimensional parameters,
Energy conversion between magnetic and kinematic energy[edit]
The scalar product of the above form of Navier-Stokes equation with gives the rate of increase of kinetic energy density, , on the left-hand side. The last term on the right-hand side is then , the local contribution to the kinetic energy due to Lorentz force.
The scalar product of the induction equation with gives the rate of increase of the magnetic energy density, , on the left-hand side. The last term on the right-hand side is then Since the equation is volume-integrated, this term is equivalent up to a boundary term (and with the double use of the scalar triple product identity) to (where one of Maxwell's equations was used). This is the local contribution to the magnetic energy due to fluid motion.
Thus the term is the rate of transformation of kinetic energy to magnetic energy. This has to be non-negative at least in part of the volume, for the dynamo to produce magnetic field.[19]
From the diagram above, it is not clear why this term should be positive. A simple argument can be based on consideration of net effects. To create the magnetic field, the net electric current must wrap around the axis of rotation of the planet. In that case, for the term to be positive, the net flow of conducting matter must be towards the axis of rotation. The diagram only shows a net flow from the poles to the equator. However mass conservation requires an additional flow from the equator toward the poles. If that flow was along the axis of rotation, that implies the circulation would be completed by a flow from the ones shown towards the axis of rotation, producing the desired effect.
Order of magnitude of the magnetic field created by Earth's dynamo[edit]
The above formula for the rate of conversion of kinetic energy to magnetic energy, is equivalent to a rate of work done by a force of on the outer core matter, whose velocity is . This work is the result of non-magnetic forces acting on the fluid.
Of those, the gravitational force and the centrifugal force are conservative and therefore have no overall contribution to fluid moving in closed loops. Ekman number (defined above), which is the ratio between the two remaining forces, namely the viscosity and Coriolis force, is very low inside Earth's outer core, because its viscosity is low (1.2–1.5 ×10−2 pascal-second[20]) due to its liquidity.
Thus the main time-averaged contribution to the work is from Coriolis force, whose size is though this quantity and are related only indirectly and are not in general equal locally (thus they affect each other but not in the same place and time).
The current density J is itself the result of the magnetic field according to Ohm's law. Again, due to matter motion and current flow, this is not necessarily the field at the same place and time. However these relations can still be used to deduce orders of magnitude of the quantities in question.
In terms of order of magnitude, and , giving or:
The exact ratio between both sides is the square root of Elsasser number.
Note that the magnetic field direction cannot be inferred from this approximation (at least not its sign) as it appears squared, and is, indeed, sometimes reversed, though in general it lies on a similar axis to that of .
For earth outer core, ρ is approximately 104 kg/m3,[20] Ω = 2π/day = 7.3×10−5/second and σ is approximately 107Ω−1m−1 .[21] This gives 2.7×10−4 Tesla.
The magnetic field of a magnetic dipole has an inverse cubic dependence in distance, so its order of magnitude at the earth surface can be approximated by multiplying the above result with (Router core⁄REarth )3 = (2890⁄6370)3 = 0.093 , giving 2.5×10−5 Tesla, not far from the measured value of 3×10−5 Tesla at the equator.
Numerical models[edit]

Broadly, models of the geodynamo attempt to produce magnetic fields consistent with observed data given certain conditions and equations as mentioned in the sections above. Implementing the magnetohydrodynamic equations successfully was of particular significance because they pushed dynamo models to self-consistency. Though geodynamo models are especially prevalent, dynamo models are not necessarily restricted to the geodynamo; solar and general dynamo models are also of interest. Studying dynamo models has utility in the field of geophysics as doing so can identify how various mechanisms form magnetic fields like those produced by astrophysical bodies like Earth and how they cause magnetic fields to exhibit certain features, such as pole reversals.
The equations used in numerical models of dynamo are highly complex. For decades, theorists were confined to two dimensional kinematic dynamo models described above, in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. The progression from linear to nonlinear, three dimensional models of dynamo was largely hindered by the search for solutions to magnetohydrodynamic equations, which eliminate the need for many of the assumptions made in kinematic models and allow self-consistency.

The first self-consistent dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan[22] and one in the United States.[23][24] The latter was made as a model with regards to the geodynamo and received significant attention because it successfully reproduced some of the characteristics of the Earth's field.[19] Following this breakthrough, there was a large swell in development of reasonable, three dimensional dynamo models.[19]
Though many self-consistent models now exist, there are significant differences among the models, both in the results they produce and the way they were developed.[19] Given the complexity of developing a geodynamo model, there are many places where discrepancies can occur such as when making assumptions involving the mechanisms that provide energy for the dynamo, when choosing values for parameters used in equations, or when normalizing equations. In spite of the many differences that may occur, most models have shared features like clear axial dipoles. In many of these models, phenomena like secular variation and geomagnetic polarity reversals have also been successfully recreated.[19]
Observations[edit]
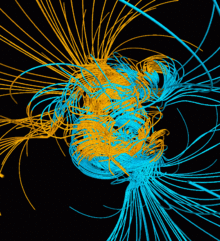
Many observations can be made from dynamo models. Models can be used to estimate how magnetic fields vary with time and can be compared to observed paleomagnetic data to find similarities between the model and the Earth. Due to the uncertainty of paleomagnetic observations, however, comparisons may not be entirely valid or useful.[19] Simplified geodynamo models have shown relationships between the dynamo number (determined by variance in rotational rates in the outer core and mirror-asymmetric convection (e.g. when convection favors one direction in the north and the other in the south)) and magnetic pole reversals as well as found similarities between the geodynamo and the Sun's dynamo.[19] In many models, it appears that magnetic fields have somewhat random magnitudes that follow a normal trend that average to zero.[19] In addition to these observations, general observations about the mechanisms powering the geodynamo can be made based on how accurately the model reflects actual data collected from Earth.
Modern modelling[edit]
The complexity of dynamo modelling is so great that models of the geodynamo are limited by the current power of supercomputers, particularly because calculating the Ekman and Rayleigh number of the outer core is extremely difficult and requires a vast number of computations.
Many improvements have been proposed in dynamo modelling since the self-consistent breakthrough in 1995. One suggestion in studying the complex magnetic field changes is applying spectral methods to simplify computations.[25] Ultimately, until considerable improvements in computer power are made, the methods for computing realistic dynamo models will have to be made more efficient, so making improvements in methods for computing the model is of high importance for the advancement of numerical dynamo modelling.
Notable people[edit]
- Stanislav I. Braginsky, research geophysicist
See also[edit]
References[edit]
- ^ "How does the Earth's core generate a magnetic field?". USGS FAQs. United States Geological Survey. Archived from the original on 18 January 2015. Retrieved 21 October 2013.
- ^ Ampère, André-Marie (1822). Recueil d'observations électro-dynamiques : contenant divers mémoires, notices, extraits de lettres ou d'ouvrages périodiques sur les sciences relatifs à l'action mutuelle de deux courants électriques, à celle qui existe entre un courant électrique et un aimant ou le globe terrestre, et à celle de deux aimants l'un sur l'autre (in French). Paris: Crochard.[ISBN unspecified]
- ^ Larmor, J. (1919). "How could a rotating body such as the Sun become a magnet?". Reports of the British Association. 87: 159–160.
- ^ Larmor, J. (1919). "Possible rotational origin of magnetic fields of sun and earth". Electrical Review. 85: 412ff. Reprinted in Engineering, vol. 108, pages 461ff (3 October 1919).
- ^ Nye, Mary Jo (1 March 1999). "Temptations of theory, strategies of evidence: P. M. S. Blackett and the earth's magnetism, 1947–52". The British Journal for the History of Science. 32 (1): 69–92. doi:10.1017/S0007087498003495. S2CID 143344977.
- ^ Merrill, McElhinny & McFadden 1996, page 17 claim that in 1905, shortly after composing his special relativity paper, Albert Einstein described the origin of the Earth's magnetic field as being one of the great unsolved problems facing modern physicists. However, they do not provide details on where he made this statement.
- ^ Sanders, Robert (2003-12-10). "Radioactive potassium may be major heat source in Earth's core". UC Berkeley News. Retrieved 2007-02-28.
- ^ Sakuraba, Ataru; Paul H. Roberts (4 October 2009). "Generation of a strong magnetic field using uniform heat flux at the surface of the core". Nature Geoscience. 2 (11): 802–805. Bibcode:2009NatGe...2..802S. doi:10.1038/ngeo643.
- ^ Buffett, Bruce (2009). "Geodynamo: A matter of boundaries". Nature Geoscience. 2 (11): 741–742. Bibcode:2009NatGe...2..741B. doi:10.1038/ngeo673.
- ^ Brandenburg, Axel (2007). "Hydromagnetic dynamo theory". Scholarpedia. 2 (3): 2309. Bibcode:2007SchpJ...2.2309B. doi:10.4249/scholarpedia.2309.
- ^ E. Pallé (2010). The Earth as a Distant Planet: A Rosetta Stone for the Search of Earth-Like Worlds (Astronomy and Astrophysics Library). Berlin: Springer. pp. 316–317. ISBN 978-1-4419-1683-9. Retrieved 17 July 2010.
- ^ Steigerwald, Bill (October 6, 2010). "Saturn's Icy Moon May Keep Oceans Liquid with Wobble". NASA. Archived from the original on March 24, 2015. Retrieved August 14, 2012.
- ^ Cassis, Nikki (March 19, 2012). "Geologic map of Jupiter's moon Io details an otherworldly volcanic surface". Astrogeology Science Center. Retrieved August 14, 2012.[permanent dead link]
- ^ "Mercury's Surprising Core and Landscape Curiosities". MESSENGER. Carnegie Institution for Science. March 21, 2012. Archived from the original on January 18, 2015. Retrieved August 14, 2012.
- ^ Stevens, Tim (November 9, 2011). "Ancient lunar dynamo may explain magnetized moon rocks". University of California. Retrieved August 14, 2012.
- ^ Ovchinnikov, I.V.; Ensslin, T.A. (April 2016). "Kinematic dynamo, supersymmetry breaking, and chaos". Physical Review D. 93 (8): 085023. arXiv:1512.01651. Bibcode:2016PhRvD..93h5023O. doi:10.1103/PhysRevD.93.085023. S2CID 59367815.
- ^ Ovchinnikov, I.V. (March 2016). "Introduction to Supersymmetric Theory of Stochastics". Entropy. 18 (4): 108. arXiv:1511.03393. Bibcode:2016Entrp..18..108O. doi:10.3390/e18040108. S2CID 2388285.
- ^ Parker, Eugene N. (September 1955). "Hydromagnetic Dynamo Models". The Astrophysical Journal. 122: 293–314. Bibcode:1955ApJ...122..293P. doi:10.1086/146087.
- ^ a b c d e f g h i Kono, Masaru; Roberts, Paul H. (2002). "Recent geodynamo simulations and observations of the geomagnetic field". Reviews of Geophysics. 40 (4): 1–53. Bibcode:2002RvGeo..40.1013K. doi:10.1029/2000RG000102.
- ^ a b de Wijs, G. A., Kresse, G., Vočadlo, L., Dobson, D., Alfe, D., Gillan, M. J., & Price, G. D. (1998). The viscosity of liquid iron at the physical conditions of the Earth's core. Nature, 392(6678), 805.
- ^ Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., & Ohishi, Y. (2016). Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature, 534(7605), 95. Link to a summary
- ^ Kageyama, Akira; Sato, Tetsuya (1 January 1995). "Computer simulation of a magnetohydrodynamic dynamo. II". Physics of Plasmas. 2 (5): 1421–1431. Bibcode:1995PhPl....2.1421K. doi:10.1063/1.871485.
- ^ Glatzmaier, Gary A.; Roberts, Paul H. (1995). "A three-dimensional self-consistent computer simulation of a geomagnetic field reversal". Nature. 377 (6546): 203–209. Bibcode:1995Natur.377..203G. doi:10.1038/377203a0. S2CID 4265765.
- ^ Glatzmaier, G; Roberts, Paul H. (1995). "A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle". Physics of the Earth and Planetary Interiors. 91 (1–3): 63–75. Bibcode:1995PEPI...91...63G. doi:10.1016/0031-9201(95)03049-3.
- ^ Avery, Margaret S.; Constable, Catherine G.; Davies, Christopher J.; Gubbins, David (2019-01-01). "Spectral methods for analyzing energy balances in geodynamo simulations" (PDF). Physics of the Earth and Planetary Interiors. 286: 127–137. Bibcode:2019PEPI..286..127A. doi:10.1016/j.pepi.2018.10.002. ISSN 0031-9201.
- Demorest, Paul (21 May 2001). "Dynamo Theory and Earth's magnetic Field (term paper)" (PDF). Archived from the original (PDF) on 21 February 2007. Retrieved 14 October 2011.
- Fitzpatrick, Richard (18 May 2002). "MHD Dynamo Theory". Plasma Physics. University of Texas at Austin. Retrieved 14 October 2011.
- Merrill, Ronald T.; McElhinny, Michael W.; McFadden, Phillip L. (1996). The magnetic field of the earth: Paleomagnetism, the core, and the deep mantle. Academic Press. ISBN 978-0-12-491246-5.
- Stern, David P. "Chapter 12: The dynamo process". The Great Magnet, the Earth. Retrieved 14 October 2011.
- Stern, David P. "Chapter 13: Dynamo in the Earth's Core". The Great Magnet, the Earth. Retrieved 14 October 2011.






![{\displaystyle {\begin{aligned}&\nabla \cdot \mathbf {B} =0\\[1ex]&\nabla \times \mathbf {B} =\mu _{0}\mathbf {J} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffb7f07611a6797a341d97c2b5938b50097c1e74)































