Naismith's rule
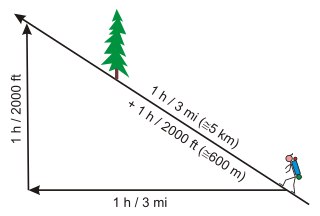
Naismith's rule helps with the planning of a walking or hiking expedition by calculating how long it will take to travel the intended route, including any extra time taken when walking uphill. This rule of thumb was devised by William W. Naismith, a Scottish mountaineer, in 1892.[1][3][4] A modern version can be formulated as follows:
- Allow one hour for every 3 miles (5 km) forward, plus an additional hour for every 2,000 feet (600 m) of ascent.[2][5]
Assumptions and calculations
[edit]
The original Naismith's rule from 1892 says that one should allow one hour per three miles on the map and an additional hour per 2000 feet of ascent.[1][4] It is included in the last sentence of his report from a trip.[1][8]
Today it is formulated in many ways. Naismith's 1 h / 3 mi + 1 h / 2000 ft can be replaced by:
- 1 h / 3 mi (5 km) + 1 h / 2000 ft (600 m)[2][5][9]
- 1 h / 5 km (3 mi) + 1/2 h / 300 m (1000 ft)[10][11][12]
- 3 mph + ½ h / 1000 ft
5 km/h + ½ h / 300 m[13][n 2] - 12 min / 1 km + 10 min / 100 m[8]
The basic rule assumes hikers of reasonable fitness, on typical terrain, and under normal conditions. It does not account for delays, such as extended breaks for rest or sightseeing, or for navigational obstacles. For planning expeditions a team leader may use Naismith's rule in putting together a route card.[citation needed]
It is possible to apply adjustments or "corrections" for more challenging terrain, although it cannot be used for scrambling routes. In the grading system used in North America, Naismith's rule applies only to hikes rated Class 1 on the Yosemite Decimal System, and not to Class 2 or higher.[citation needed]
In practice, the results of Naismith's rule are usually considered the minimum time necessary to complete a route.[citation needed]
When walking in groups, the speed of the slowest person is calculated.[13]
Naismith's rule appears in UK statute law, although not by name. The Adventure Activities Licensing Regulations apply to providers of various activities including trekking. Part of the definition of trekking is that it is over terrain on which it would take more than 30 minutes to reach a road or refuge (by the quickest safe route), based on a walking speed of 5 kilometres per hour plus an additional minute for every 10 metres of ascent.[14]

Scarf's equivalence between distance and climb
[edit]Alternatively, the rule can be used to determine the equivalent flat distance of a route. This is achieved by recognising that Naismith's rule implies an equivalence between distance and climb in time terms: 3 miles (=15,840 feet) of distance is equivalent in time terms to 2000 feet of climb.[17]
Professor Philip Scarf, Associate Dean of Research and Innovation and Professor of Applied Statistics at the University of Salford,[18] in research published in 2008, gives the following formula:[4]
- equivalent distance = x + α·y
where:
- x = horizontal distance
- y = vertical distance
- α = 7.92 (3 mi / 2000 ft[17][4][19]), called Naismith’s number by Scarf[17][4][19]
That is, 7.92 units of distance are equivalent to 1 unit of climb. For convenience an 8 to 1 rule can be used. So, for example, if a route is 20 kilometres (12 mi) with 1600 metres of climb (as is the case on leg 1 of the Bob Graham Round, Keswick to Threlkeld), the equivalent flat distance of this route is 20+(1.6×8)=32.8 kilometres (20.4 mi). Assuming an individual can maintain a speed on the flat of 5 km/h, the route will take 6 hours and 34 minutes. The simplicity of this approach is that the time taken can be easily adjusted for an individual's own (chosen) speed on the flat; at 8 km/h (flat speed) the route will take 4 hours and 6 minutes. The rule has been tested on fell running times and found to be reliable.[17] Scarf proposed this equivalence in 1998.[4][6]
As you can see, the Scarf's assumption allows also to calculate the time for each speed, not just one as in case of the original Naismith rule.
Pace
[edit]Pace is the reciprocal of speed. It can be calculated here from the following formula:[6][19]
- p = p0·(1 + α·m)
where:
- p = pace
- p0 = pace on flat terrain
- m = gradient uphill
This formula is true for m≥0 (uphill or flat terrain).[6][19] It assumes equivalence of distance and climb by applying mentioned earlier α factor.[4][19]
Sample calculations: p0 = 12 min / km (for 5 km / h speed), m = 0.6 km climb / 5 km distance = 0.12, p = 12 · (1 + 7.92 · 0.12) = 23.4 min / km.
Other modifications
[edit]Over the years several adjustments have been formulated in an attempt to make the rule more accurate by accounting for further variables such as load carried, roughness of terrain, descents and fitness (or lack of it). The accuracy of some corrections is disputed,[20] in particular the speed at which walkers descend a gentle gradient. No simple formula can encompass the full diversity of mountain conditions and individual abilities.
Tranter's corrections
[edit]Tranter's corrections make adjustments for fitness and fatigue. Fitness is determined by the time it takes to climb 1000 feet over a distance of ½ mile (800 m). Additional adjustments for uneven or unstable terrain or conditions can be estimated by dropping one or more fitness levels.
| Individual fitness in minutes | Time taken in hours estimated using Naismith's rule | |||||||||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | |
| 15 (very fit) | 1 | 1.5 | 2 | 2.75 | 3.5 | 4.5 | 5.5 | 6.75 | 7.75 | 10 | 12.5 | 14.5 | 17 | 19.5 | 22 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 1.25 | 2.25 | 3.25 | 4.5 | 5.5 | 6.5 | 7.75 | 8.75 | 10 | 12.5 | 15 | 17.5 | 20 | 23 | ||
| 25 | 1.5 | 3 | 4.25 | 5.5 | 7 | 8.5 | 10 | 11.5 | 13.25 | 15 | 17.5 | |||||
| 30 | 2 | 3.5 | 5 | 6.75 | 8.5 | 10.5 | 12.5 | 14.5 | ||||||||
| 40 | 2.75 | 4.25 | 5.75 | 7.5 | 9.5 | 11.5 | Too much to be attempted | |||||||||
| 50 (unfit) | 3.25 | 4.75 | 6.5 | 8.5 | ||||||||||||
For example, if Naismith's rule estimates a journey time of 9 hours and your fitness level is 25, you should allow 11.5 hours.
Aitken corrections
[edit]Aitken (1977) assumes that 1 h takes to cover 3 mi (5 km) on paths, tracks and roads, while this is reduced to 2½ mi (4 km) on all other surfaces.[5]
For both distances he gives an additional 1 h per 2000 ft (600 m) of ascent.[5] So Aitken doesn't take into account equivalence between distance and climb (proposed by Scarf in 1998[4][6]).
Langmuir corrections
[edit]Langmuir (1984) extends the rule on descent. He assumes the Naismith's base speed of 5 km/h and makes the following further refinements for going downhill:[13][15][21]
- For a gentle decline (slopes between 5 degrees and 12 degrees) subtract 10 minutes for every 300 meters of descent[13][15][21]
- For a steep decline (slopes greater than 12 degrees) add 10 minutes for every 300 meters of descent[15][21]
Later he says that the fitness of the slowest member of a party should be taken into account and thus a more practical formula for a group is:[13]
See also
[edit]Notes
[edit]- ^ a b Speed and pace for the Naismith rule were calculated here for its metric version (5 kilometres horizontally and 600 meters of ascent), not the original one (3 mi and 2,000 ft).
In case of Naismith rule and Langmuir corrections the same, not modified value of ascent and descent was used for the distance of 4 km as for 5 km – 600 m for the Naismith rule and 300 m for Langmuir corrections (not taking into account the equivalence between distance and climb). - ^ Langmuir 2013 recalls the Naismith's rule from 1892 in miles and feet, but further gives and uses it in metric system, climbing sometimes per contour line on a map (10 m or 50 m).[13]
References
[edit]- ^ a b c d Naismith, W. W. (September 1892). "Excursions. Cruach Ardran, Stobinian, and Ben More". Scottish Mountaineering Club Journal. 2 (3): 136. Retrieved 22 January 2017. Available also in: Google Books
- ^ a b c Holman, Tom (2010). A Lake District Miscellany. Frances Lincoln. ISBN 978-1907666384. Retrieved 19 January 2017.
- ^ Thompson, S (2010). "1865–1914: gentlemen and gymnasts". Unjustifiable risk? The story of British climbing (1st ed.). Singapore: KHL Printing. pp. 51–122. ISBN 978-1-85284-627-5.
- ^ a b c d e f g h Scarf, Philip (August 2008). "A mathematical excursion in the isochronic hills" (PDF). Mathematics Today. 44: 163–167. Retrieved 22 January 2017.
- ^ a b c d Aitken, Robert (1977). Wilderness Areas in Scotland, unpublished Ph.D. Thesis. University of Aberdeen (Ph.D). Aberdeen. Retrieved 26 January 2017.
- ^ a b c d e Kay, A. (2012). "Route Choice in Hilly Terrain" (PDF). Geogr Anal. 44 (2): 87–108. CiteSeerX 10.1.1.391.1203. doi:10.1111/j.1538-4632.2012.00838.x. S2CID 14054589. Archived from the original (PDF) on 2012-11-14. Retrieved 19 January 2017.
- ^ a b c Magyari-Sáska, Zsolt; Dombay, Ştefan (2012). "Determining minimum hiking time using DEM" (PDF). Geographia Napocensis. Anul VI (2): 124–9. Retrieved 21 March 2013.
- ^ a b MacInnes, Kellan (2013). Caleb's List: Climbing the Scottish Mountains Visible from Arthur's Seat. Luath Press Ltd. ISBN 978-1909912069.
- ^ "Naismith's rule". Maumturks Walking Club. Retrieved 22 January 2017.
- ^ Evans, Thammy (2010). Macedonia; the Bradt Travel Guide. Bradt Guides. Bradt Travel Guides. ISBN 978-1841622972.
- ^ Marsh, Terry (2012). Walking on the West Pennine Moors: 30 routes in gritstone country. Cicerone Press Limited. ISBN 978-1849655392.
- ^ Bagshaw, Chris (2006). The Ultimate Hiking Skills Handbook. David & Charles. ISBN 978-0715322543. (5 km /h (3 mph) and 1/2 hr / 300 m (1000 ft))
- ^ a b c d e f g Langmuir, Eric (2013). Mountaincraft and Leadership; A Handbook for Mountaineers and Hillwalking Leaders in the British Isles (Fourth ed.). Mountain Training England; Mountain Training Scotland. pp. 38–39. ISBN 978-0-9568869-0-3.
- ^ See definition of "travelling time" in The Adventure Activities Licensing Regulations 1996, section 2 and The Adventure Activities Licensing Regulations 2004, section 2.
- ^ a b c d Langmuir, Eric (1984). Mountaincraft and Leadership. Official Handbook of the Mountain Leader Training Boards of Great Britain and Northern Ireland. Edinburgh Scotland: Britain & Scottish Sports Council.
- ^ Tobler, W (February 1993). "Three presentations on geographical analysis and modeling: Non-isotropic geographic modeling speculations on the geometry of geography global spatial analysis" (PDF). National Center for Geographic Information and Analysis Technical Report. 93 (1): 1–24. Archived from the original (PDF) on 22 April 2008. Retrieved 21 March 2013. Available also in HTML Archived 2016-03-04 at the Wayback Machine format.
- ^ a b c d Scarf, Philip (20 Mar 2007). "Route choice in mountain navigation, Naismith's rule, and the equivalence of distance and climb". Journal of Sports Sciences. 25 (6): 719–726. doi:10.1080/02640410600874906. PMID 17454539. S2CID 13897101. Also available in: ResearchGate
- ^ "Professor Philip Scarf". www.salford.ac.uk. University of Salford. Retrieved 1 February 2018.
- ^ a b c d e Kay, A. (November 2012). "Pace and critical gradient for hill runners: an analysis of race records" (PDF). Journal of Quantitative Analysis in Sports. 8 (4). doi:10.1515/1559-0410.1456. ISSN 1559-0410. S2CID 15045011. Retrieved 19 January 2017.
- ^ of downhill correction for Naismith's rule
- ^ a b c Caffin, Roger. "FAQ - Navigation: Walking Speed - Naismith's Rule". Retrieved 23 March 2013.
External links
[edit]- Online Naismith's rule hiking time calculator, plus adjustments for intended pace, trail conditions, and pack weight.
- About walking uphill: time required, energy consumption and the zigzag transition
- Naismith's Rule[permanent dead link]
- An online calculator and Nomogram
- Naismith's Rule and Route Timing
- Tranter's Correction – is it still relevant?[permanent dead link]
