Jump to content

Pyknon

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by Citation bot (talk | contribs) at 22:48, 21 November 2022 (Add: doi, s2cid. | Use this bot. Report bugs. | Suggested by Whoop whoop pull up | #UCB_webform 95/578). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

Pyknon (from Greek: πυκνόν), sometimes also transliterated as pycnon (from Greek: πυκνός close, close-packed, crowded, condensed; Template:Lang-lat) in the music theory of Antiquity is a structural property of any tetrachord in which a composite of two smaller intervals is less than the remaining (incomposite) interval. The makeup of the pyknon serves to identify the melodic genus (also called "genus of a tetrachord") and the octave species made by compounding two such tetrachords, and the rules governing the ways in which such compounds may be made centre on the relationships of the two pykna involved.

Definition

Look up pyknon in Wiktionary, the free dictionary.

The pyknon was an important criterion in the classification of melodic genera (Greek: γένη τῶν μελῳδουμένων). The Greek word πυκνόν is an adjective meaning "close", "compact", "close-packed", or "crowded".[1] In Ancient Greek music theory, this term is used to describe a pair of intervals within a tetrachord, the sum of which is less than the remainder of the tetrachord.[2] Although in modern usage, a tetrachord may be any four-note segment of a scale, or indeed any (unordered) collection of four pitch classes, in ancient Greek music theory a tetrachord consists of a four-note segment of the Greater and Lesser Perfect Systems bounded by the interval of a perfect fourth, the outer notes of which remain fixed in all genera and therefore are called "standing notes" (Greek: ἑστῶτες φθόγγοι). The positions of the inner notes vary from one genus to another, for which reason they are called "movable notes".[3] In its basic theoretical form, the largest interval of a tetrachord is at the top, and the smallest at the bottom. The existence of a pyknon therefore depends on the uppermost interval being larger than half of a perfect fourth, which occurs only in the chromatic and enharmonic genera. Because the diatonic genus consists of two whole tones and one semitone, no single interval is larger than the other two combined, and so there is no pyknon.[4] For this reason, the enharmonic and chromatic genera are sometimes called the "pyknic genera", in order to distinguish them from the diatonic.[5]

Theoretical applications

The notes of the central tetrachord of the system in ascending order are hypate, parhypate, lichanos (or hypermese), and mese. A second tetrachord is added above, after a disjunctive tone, and the corresponding names (together with the interval ratios of the standing tones) are:[6]

  • mese (4:3) – nete (2:1) (standing)
  • lichanos – paranete (movable)
  • parhypate – trite (movable)
  • hypate (1:1) – paramese (3:2) (standing)

Although movable, the lichanos must remain above the parhypate, and the paranete above the trite.[7]

A "composite interval" is one made up of two or more smaller intervals; an "incomposite interval" has no smaller components In these terms, if the composite interval between the hypate and the lichanos (or paramese and paranete) is smaller than the incomposite interval from the lichanos to the mese (or paranete to nete), the three notes in that composite interval are together called a pyknon.[7] In the diatonic genus, because the composite interval from hypate to lichanos (a minor third) is larger than the remaining incomposite interval from lichanos to mese (a whole tone), the lowest three notes of the diatonic tetrachord are designated apyknon: "not close-packed".[8]

Enharmonic

Two pyknic enharmonic tetrachords, together comprising the Greek Dorian octave species in the enharmonic genus

In the enharmonic genus, the large incomposite interval was originally a ditone (the major third of Pythagorean tuning), leaving a pyknon with a total width of just a semitone. The Pythagorean ditone is equivalent to two 9:8 epogdoa, or major seconds), together an interval of 81:64, thus leaving a pyknon of 256:243—a limma (minor Pythagorean semitone), but how the pyknon was exactly (that is by exact mathematic calculation) divided into its two component intervals is not known.[9] The tuning of Eratosthenes, as reported by Aristoxenus, uses a major third of 19:15 with the two unequal intervals of the pyknon in the ratios of 40:39 and 39:38.[10] Although Aristoxenus also implies that the two intervals of the pyknon in the enharmonic genus may be equal,[11] the anonymous author of the Euclidean Sectio Canonis (P18) is unequivocal: "The parhypatai and tritai do not divide the pyknon into equal intervals".[12]

Ptolemy reports in his Harmonics (2. 14) that two other theorists, Archytas and Didymus, replaced the ditone with the smaller, just major third with the number ratio of 5:4, making the pyknon correspondingly larger.[13] This pyknon was divided differently by these two theorists, but in both cases the two intervals were not equal to one another. Archytas, who was the first theorist to give ratios for all of the genera, chose 28:27 and 36:35, and Didymus, some four centuries later, gave 32:31 and 31:30.[14]

Chromatic

Two pyknic chromatic tetrachords, together comprising the Greek Dorian octave species in the chromatic genus

In the chromatic genus, the largest interval was called a Greek: τριημιτόνιόν ἀσύνθετον, Template:Lang-lat—translated as "incomposite" (or "noncomposite") "trihemitone" (Bower, Hagel, Levin, and Barker prefer a descriptive translation, "an individed interval of three semitones";[15][16][17][18] Strunk uses "trisemitone"[19]), the modern term being "minor third"—leaving a pyknon of some type of whole tone to be divided into two semitones. There is a larger number of variations in the tuning of the chromatic than in the enharmonic. Up to the beginning of the 4th century BC the chromatic pyknon spanned a major whole tone with a 9:8 ratio, and this was divided by Gaudentius into ascending semitone intervals of 256:243 and 2187:2048.[10] Ptolemy defined two different tunings of the chromatic genus: the "soft" chromatic with a smaller pyknon and the "intense" chromatic with a larger one. The unequal semitones dividing the pykna were in ratios of 28:27 and 15:14 for the soft chromatic and 22:21 and 12:11 for the intense. The larger remaining interval was 6:5 in the soft chromatic and 7:6 in the intense.[9]

Scale structure

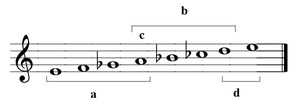
Greek Mixolydian octave species on E in the chromatic genus: conjunct tetrachords a and b, with note of conjunction c, and interval of disjunction d; the two pykna are separated by the larger interval between steps 3 and 4 Playⓘ

A further refinement of tetrachordal construction, according to Aristoxenus, is that the lower interval of the pyknon must be smaller than or equal to the upper one.[20] Didymus in the chromatic genus and Archytas in the enharmonic broke this rule, however, and in the Harmonics (2. 13) Ptolemy criticized this feature in Didymus, holding that it is unmelodic and out of agreement with the evidence of our ears.[13]

According to Aristoxenus' Elementa harmonica (Elements of Harmony, book 2), whenever tetrachords are combined to form a scale filling an octave, "Two consecutive pycna may not occur in ascent or descent. A ditone may precede or follow [a pycnon] in ascent or descent. A tone may follow [a pycnon] only in descent".[21]

References

  • Barbera, André (1977). "Arithmetic and Geometric Divisions of the Tetrachord". Journal of Music Theory. 21 (2 - Autumn): 294–323. doi:10.2307/843492. JSTOR 843492.
  • Barbera, André (1984). "Octave Species". The Journal of Musicology. 3 (3 - Summer): 229–241. doi:10.2307/763813. JSTOR 763813.
  • Barker, Andrew (1981). "Methods and Aims in the Euclidean Sectio Canonis". Journal of Hellenic Studies. 101: 1–16. doi:10.2307/629840. JSTOR 629840. S2CID 162356270.
  • Chalmers, John (1990). Larry Polansky; Carter Scholz (eds.). Divisions of the Tetrachord. Lebanon NH: Frog Peak Music. ISBN 0-945996-04-7.
  • Levin, Flora R. (2007). "Ἀπειρία in Aristoxenian Theory". Hermes. 135 (4): 406–428. doi:10.25162/hermes-2007-0038. S2CID 151484983.
  • Mathiesen, Thomas J. (1999). Apollo's Lyre: Greek Music and Music Theory in Antiquity and the Middle Ages. Lincoln: University of Nebraska Press. ISBN 9780803230798.
  • Solomon, Jon (1984). "Towards a History of Tonoi". The Journal of Musicology. 3 (3 - Summer): 242–251. doi:10.2307/763814. JSTOR 763814.

Footnotes

  1. ^ Liddell, Henry George, and Robert Scott. 1996. A Greek-English Lexicon, ninth edition, revised and augmented throughout by Sir Henry Stuart Jones and Roderick McKenzie. Oxford: Clarendon Press; New York City: Oxford University Press. ISBN 0-19-864226-1.
  2. ^ Levin 2007, p. 413.
  3. ^ Mathiesen 1999, pp. 301, 312, 322, 344, 350, et passim; from Greek: κινούμενοι φθόγγοι.
  4. ^ Barbera 1984, p. 229.
  5. ^ Solomon 1984, p. 246.
  6. ^ Chalmers 1990, p. 4; Mathiesen 1999, p. 245.
  7. ^ a b Mathiesen 1999, p. 312.
  8. ^ Barbera 1977, p. 321n11.
  9. ^ a b Chalmers 1990, p. 9.
  10. ^ a b Chalmers 1990, p. 8.
  11. ^ Mathiesen 1999, p. 333.
  12. ^ Barker 1981, p. 6.
  13. ^ a b West, M[artin]. L[itchfield]. 1992. Ancient Greek Music. Oxford: Clarendon Press; New York: Oxford University Press. p. 170. ISBN 0198149751 (pbk.); ISBN 0585229929 (electronic bk.).
  14. ^ Chalmers 1990, pp. 7–8.
  15. ^ Bower, Calvin (1989). Fundamentals of Music. Anicius Manlius Severinus Boethius. Translated, with Introduction and Notes by Calvin M. Bower. New Haven and London: Yale University Press. p. 43.
  16. ^ Hagel, Stephan (2009). Ancient Greek Music. A New Technical History. Cambridge University Press. pp. 105, 266–7. ISBN 9780521517645.
  17. ^ Levin, Flora R. (1994). The Manual of Harmonics of Nicomachus the Pythagorean. Translation and commentary by Flora R. Levin. Grand Rapids MI: Phanes Press. pp. 125, 174.
  18. ^ Barker, Andrew (1989). Greek Musical Writings. Vol. II: Harmonic and Acoustic Theory. Cambridge University Press. pp. 261, 267.
  19. ^ Strunk, Oliver. 1998. Source Readings in Music History. Revised Edition by Leo Treitler. New York City, London: W. W. Norton and Company. pp. 36-7.
  20. ^ Barbera 1984, pp. 229–30.
  21. ^ Mathiesen 1999, p. 331.

Further reading

  • Mathiesen Thomas J. 2001. "Greece, §I: Ancient", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
  • Winnington-Ingram, Reginald Pepys. 1936. Mode in Ancient Greek Music. Cambridge Classical Studies 2. Cambridge: The University Press. Reprinted, Chicago, Argonaut Inc., 1967; Amsterdam: Adolf M. Hakkert, 1968.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Pyknon&oldid=1123114139"