Rectangular lattice

|

|
| Primitive | Centered |
|---|---|

|

|
| pmm | cmm |
The rectangular lattice and rhombic lattice (or centered rectangular lattice) constitute two of the five two-dimensional Bravais lattice types.[1] The symmetry categories of these lattices are wallpaper groups pmm and cmm respectively. The conventional translation vectors of the rectangular lattices form an angle of 90° and are of unequal lengths.
Bravais lattices
[edit]There are two rectangular Bravais lattices: primitive rectangular and centered rectangular (also rhombic).
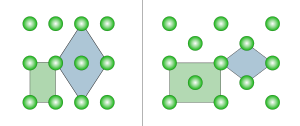
| Bravais lattice | Rectangular | Centered rectangular |
|---|---|---|
| Pearson symbol | op | oc |
| Standard unit cell | 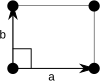
|
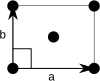
|
| Rhombic unit cell | 
|

|
The primitive rectangular lattice can also be described by a centered rhombic unit cell, while the centered rectangular lattice can also be described by a primitive rhombic unit cell. Note that the length in the lower row is not the same as in the upper row. For the first column above, of the second row equals of the first row, and for the second column it equals .
Crystal classes
[edit]The rectangular lattice class names, Schönflies notation, Hermann-Mauguin notation, orbifold notation, Coxeter notation, and wallpaper groups are listed in the table below.
| Geometric class, point group | Arithmetic class |
Wallpaper groups | ||||
|---|---|---|---|---|---|---|
| Schön. | Intl | Orb. | Cox. | |||
| D1 | m | (*) | [ ] | Along | pm (**) |
pg (××) |
| Between | cm (*×) |
|||||
| D2 | 2mm | (*22) | [2] | Along | pmm (*2222) |
pmg (22*) |
| Between | cmm (2*22) |
pgg (22×) | ||||
References
[edit]- ^ Rana, Farhan. "Lattices in 1D, 2D, and 3D" (PDF). Cornell University. Archived (PDF) from the original on 2020-12-18.



