Super-resolution imaging
This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. (October 2019) |
Super-resolution imaging (SR) is a class of techniques that enhance (increase) the resolution of an imaging system. In optical SR the diffraction limit of systems is transcended, while in geometrical SR the resolution of digital imaging sensors is enhanced.
In some radar and sonar imaging applications (e.g. magnetic resonance imaging (MRI), high-resolution computed tomography), subspace decomposition-based methods (e.g. MUSIC[1]) and compressed sensing-based algorithms (e.g., SAMV[2]) are employed to achieve SR over standard periodogram algorithm.
Super-resolution imaging techniques are used in general image processing and in super-resolution microscopy.
Basic concepts[edit]
Because some of the ideas surrounding super-resolution raise fundamental issues, there is need at the outset to examine the relevant physical and information-theoretical principles:
- Diffraction limit: The detail of a physical object that an optical instrument can reproduce in an image has limits that are mandated by laws of physics, whether formulated by the diffraction equations in the wave theory of light[3] or equivalently the uncertainty principle for photons in quantum mechanics.[4] Information transfer can never be increased beyond this boundary, but packets outside the limits can be cleverly swapped for (or multiplexed with) some inside it.[5] One does not so much “break” as “run around” the diffraction limit. New procedures probing electro-magnetic disturbances at the molecular level (in the so-called near field)[6] remain fully consistent with Maxwell's equations.
- Spatial-frequency domain: A succinct expression of the diffraction limit is given in the spatial-frequency domain. In Fourier optics light distributions are expressed as superpositions of a series of grating light patterns in a range of fringe widths, technically spatial frequencies. It is generally taught that diffraction theory stipulates an upper limit, the cut-off spatial-frequency, beyond which pattern elements fail to be transferred into the optical image, i.e., are not resolved. But in fact what is set by diffraction theory is the width of the passband, not a fixed upper limit. No laws of physics are broken when a spatial frequency band beyond the cut-off spatial frequency is swapped for one inside it: this has long been implemented in dark-field microscopy. Nor are information-theoretical rules broken when superimposing several bands,[7][8][9] disentangling them in the received image needs assumptions of object invariance during multiple exposures, i.e., the substitution of one kind of uncertainty for another.
- Information: When the term super-resolution is used in techniques of inferring object details from statistical treatment of the image within standard resolution limits, for example, averaging multiple exposures, it involves an exchange of one kind of information (extracting signal from noise) for another (the assumption that the target has remained invariant).
- Resolution and localization: True resolution involves the distinction of whether a target, e.g. a star or a spectral line, is single or double, ordinarily requiring separable peaks in the image. When a target is known to be single, its location can be determined with higher precision than the image width by finding the centroid (center of gravity) of its image light distribution. The word ultra-resolution had been proposed for this process[10] but it did not catch on, and the high-precision localization procedure is typically referred to as super-resolution.
The technical achievements of enhancing the performance of imaging-forming and –sensing devices now classified as super-resolution utilize to the fullest but always stay within the bounds imposed by the laws of physics and information theory.
Techniques[edit]
This section needs to be updated. The reason given is: We should update this to include progress in improving superresolution with machine learning and neural networks.. (January 2023) |
Optical or diffractive super-resolution[edit]
Substituting spatial-frequency bands: Though the bandwidth allowable by diffraction is fixed, it can be positioned anywhere in the spatial-frequency spectrum. Dark-field illumination in microscopy is an example. See also aperture synthesis.

Multiplexing spatial-frequency bands[edit]
An image is formed using the normal passband of the optical device. Then some known light structure, for example a set of light fringes that need not even be within the passband, is superimposed on the target.[8][9] The image now contains components resulting from the combination of the target and the superimposed light structure, e.g. moiré fringes, and carries information about target detail which simple unstructured illumination does not. The “superresolved” components, however, need disentangling to be revealed. For an example, see structured illumination (figure to left).
Multiple parameter use within traditional diffraction limit[edit]
If a target has no special polarization or wavelength properties, two polarization states or non-overlapping wavelength regions can be used to encode target details, one in a spatial-frequency band inside the cut-off limit the other beyond it. Both would utilize normal passband transmission but are then separately decoded to reconstitute target structure with extended resolution.
Probing near-field electromagnetic disturbance[edit]
The usual discussion of super-resolution involved conventional imagery of an object by an optical system. But modern technology allows probing the electromagnetic disturbance within molecular distances of the source[6] which has superior resolution properties, see also evanescent waves and the development of the new Super lens.
Geometrical or image-processing super-resolution[edit]

Multi-exposure image noise reduction[edit]
When an image is degraded by noise, there can be more detail in the average of many exposures, even within the diffraction limit. See example on the right.
Single-frame deblurring[edit]
Known defects in a given imaging situation, such as defocus or aberrations, can sometimes be mitigated in whole or in part by suitable spatial-frequency filtering of even a single image. Such procedures all stay within the diffraction-mandated passband, and do not extend it.
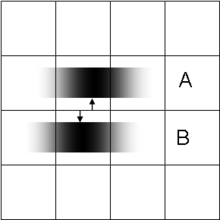
Sub-pixel image localization[edit]
The location of a single source can be determined by computing the "center of gravity" (centroid) of the light distribution extending over several adjacent pixels (see figure on the left). Provided that there is enough light, this can be achieved with arbitrary precision, very much better than pixel width of the detecting apparatus and the resolution limit for the decision of whether the source is single or double. This technique, which requires the presupposition that all the light comes from a single source, is at the basis of what has become known as super-resolution microscopy, e.g. stochastic optical reconstruction microscopy (STORM), where fluorescent probes attached to molecules give nanoscale distance information. It is also the mechanism underlying visual hyperacuity.[11]
Bayesian induction beyond traditional diffraction limit[edit]
Some object features, though beyond the diffraction limit, may be known to be associated with other object features that are within the limits and hence contained in the image. Then conclusions can be drawn, using statistical methods, from the available image data about the presence of the full object.[12] The classical example is Toraldo di Francia's proposition[13] of judging whether an image is that of a single or double star by determining whether its width exceeds the spread from a single star. This can be achieved at separations well below the classical resolution bounds, and requires the prior limitation to the choice "single or double?"
The approach can take the form of extrapolating the image in the frequency domain, by assuming that the object is an analytic function, and that we can exactly know the function values in some interval. This method is severely limited by the ever-present noise in digital imaging systems, but it can work for radar, astronomy, microscopy or magnetic resonance imaging.[14] More recently, a fast single image super-resolution algorithm based on a closed-form solution to problems has been proposed and demonstrated to accelerate most of the existing Bayesian super-resolution methods significantly.[15]
Aliasing[edit]
Geometrical SR reconstruction algorithms are possible if and only if the input low resolution images have been under-sampled and therefore contain aliasing. Because of this aliasing, the high-frequency content of the desired reconstruction image is embedded in the low-frequency content of each of the observed images. Given a sufficient number of observation images, and if the set of observations vary in their phase (i.e. if the images of the scene are shifted by a sub-pixel amount), then the phase information can be used to separate the aliased high-frequency content from the true low-frequency content, and the full-resolution image can be accurately reconstructed.[16]
In practice, this frequency-based approach is not used for reconstruction, but even in the case of spatial approaches (e.g. shift-add fusion[17]), the presence of aliasing is still a necessary condition for SR reconstruction.
Technical implementations[edit]
There are many both single-frame and multiple-frame variants of SR. Multiple-frame SR uses the sub-pixel shifts between multiple low resolution images of the same scene. It creates an improved resolution image fusing information from all low resolution images, and the created higher resolution images are better descriptions of the scene. Single-frame SR methods attempt to magnify the image without producing blur. These methods use other parts of the low resolution images, or other unrelated images, to guess what the high-resolution image should look like. Algorithms can also be divided by their domain: frequency or space domain. Originally, super-resolution methods worked well only on grayscale images,[18] but researchers have found methods to adapt them to color camera images.[17] Recently, the use of super-resolution for 3D data has also been shown.[19]
Research[edit]
There is promising research on using deep convolutional networks to perform super-resolution.[20] In particular work has been demonstrated showing the transformation of a 20x microscope image of pollen grains into a 1500x scanning electron microscope image using it.[21] While this technique can increase the information content of an image, there is no guarantee that the upscaled features exist in the original image and deep convolutional upscalers should not be used in analytical applications with ambiguous inputs.[22][23] These methods can hallucinate image features, which can make them unsafe for medical use.[24]
See also[edit]
References[edit]
- ^ Schmidt, R.O, "Multiple Emitter Location and Signal Parameter Estimation," IEEE Trans. Antennas Propagation, Vol. AP-34 (March 1986), pp.276-280.
- ^ Abeida, Habti; Zhang, Qilin; Li, Jian; Merabtine, Nadjim (2013). "Iterative Sparse Asymptotic Minimum Variance Based Approaches for Array Processing" (PDF). IEEE Transactions on Signal Processing. 61 (4): 933–944. arXiv:1802.03070. Bibcode:2013ITSP...61..933A. doi:10.1109/tsp.2012.2231676. ISSN 1053-587X. S2CID 16276001.
- ^ Born M, Wolf E, Principles of Optics, Cambridge Univ. Press, any edition
- ^ Fox M, 2007 Quantum Optics Oxford
- ^ Zalevsky Z, Mendlovic D. 2003 Optical Superresolution Springer
- ^ a b Betzig, E; Trautman, JK (1992). "Near-field optics: microscopy, spectroscopy, and surface modification beyond the diffraction limit". Science. 257 (5067): 189–195. Bibcode:1992Sci...257..189B. doi:10.1126/science.257.5067.189. PMID 17794749. S2CID 38041885.
- ^ Lukosz, W., 1966. Optical systems with resolving power exceeding the classical limit. J. opt. soc. Am. 56, 1463–1472.
- ^ a b Guerra, John M. (1995-06-26). "Super-resolution through illumination by diffraction-born evanescent waves". Applied Physics Letters. 66 (26): 3555–3557. Bibcode:1995ApPhL..66.3555G. doi:10.1063/1.113814. ISSN 0003-6951.
- ^ a b Gustaffsson, M., 2000. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microscopy 198, 82–87.
- ^ Cox, I.J., Sheppard, C.J.R., 1986. Information capacity and resolution in an optical system. J.opt. Soc. Am. A 3, 1152–1158
- ^ Westheimer, G (2012). "Optical superresolution and visual hyperacuity". Prog Retin Eye Res. 31 (5): 467–80. doi:10.1016/j.preteyeres.2012.05.001. PMID 22634484.
- ^ Harris, J.L., 1964. Resolving power and decision making. J. opt. soc. Am. 54, 606–611.
- ^ Toraldo di Francia, G., 1955. Resolving power and information. J. opt. soc. Am. 45, 497–501.
- ^ D. Poot, B. Jeurissen, Y. Bastiaensen, J. Veraart, W. Van Hecke, P. M. Parizel, and J. Sijbers, "Super-Resolution for Multislice Diffusion Tensor Imaging", Magnetic Resonance in Medicine, (2012)
- ^ N. Zhao, Q. Wei, A. Basarab, N. Dobigeon, D. Kouamé and J-Y. Tourneret, "Fast single image super-resolution using a new analytical solution for problems", IEEE Trans. Image Process., 2016, to appear.
- ^ J. Simpkins, R.L. Stevenson, "An Introduction to Super-Resolution Imaging." Mathematical Optics: Classical, Quantum, and Computational Methods, Ed. V. Lakshminarayanan, M. Calvo, and T. Alieva. CRC Press, 2012. 539-564.
- ^ a b S. Farsiu, D. Robinson, M. Elad, and P. Milanfar, "Fast and Robust Multi-frame Super-resolution", IEEE Transactions on Image Processing, vol. 13, no. 10, pp. 1327–1344, October 2004.
- ^ P. Cheeseman, B. Kanefsky, R. Kraft, and J. Stutz, 1994
- ^ S. Schuon, C. Theobalt, J. Davis, and S. Thrun, "LidarBoost: Depth Superresolution for ToF 3D Shape Scanning", In Proceedings of IEEE CVPR 2009
- ^ Johnson, Justin; Alahi, Alexandre; Fei-Fei, Li (2016-03-26). "Perceptual Losses for Real-Time Style Transfer and Super-Resolution". arXiv:1603.08155 [cs.CV].
- ^ Grant-Jacob, James A; Mackay, Benita S; Baker, James A G; Xie, Yunhui; Heath, Daniel J; Loxham, Matthew; Eason, Robert W; Mills, Ben (2019-06-18). "A neural lens for super-resolution biological imaging". Journal of Physics Communications. 3 (6): 065004. Bibcode:2019JPhCo...3f5004G. doi:10.1088/2399-6528/ab267d. ISSN 2399-6528.
- ^ Blau, Yochai; Michaeli, Tomer (2018). The perception-distortion tradeoff. IEEE Conference on Computer Vision and Pattern Recognition. pp. 6228–6237. arXiv:1711.06077. doi:10.1109/CVPR.2018.00652.
- ^ Zeeberg, Amos (2023-08-23). "The AI Tools Making Images Look Better". Quanta Magazine. Retrieved 2023-08-28.
- ^ Cohen, Joseph Paul; Luck, Margaux; Honari, Sina (2018). "Distribution Matching Losses Can Hallucinate Features in Medical Image Translation". In Alejandro F. Frangi; Julia A. Schnabel; Christos Davatzikos; Carlos Alberola-López; Gabor Fichtinger (eds.). Medical Image Computing and Computer Assisted Intervention – MICCAI 2018. 21st International Conference, Granada, Spain, September 16–20, 2018, Proceedings, Part I. Lecture Notes in Computer Science. Vol. 11070. pp. 529–536. arXiv:1805.08841. doi:10.1007/978-3-030-00928-1_60. ISBN 978-3-030-00927-4. S2CID 43919703. Retrieved 1 May 2022.
[edit]
- Curtis, Craig H.; Milster, Tom D. (October 1992). "Analysis of Superresolution in Magneto-Optic Data Storage Devices". Applied Optics. 31 (29): 6272–6279. Bibcode:1992ApOpt..31.6272M. doi:10.1364/AO.31.006272. PMID 20733840.
- Zalevsky, Z.; Mendlovic, D. (2003). Optical Superresolution. Springer. ISBN 978-0-387-00591-1.
- Caron, J.N. (September 2004). "Rapid supersampling of multiframe sequences by use of blind deconvolution". Optics Letters. 29 (17): 1986–1988. Bibcode:2004OptL...29.1986C. doi:10.1364/OL.29.001986. PMID 15455755.
- Clement, G.T.; Huttunen, J.; Hynynen, K. (2005). "Superresolution ultrasound imaging using back-projected reconstruction". Journal of the Acoustical Society of America. 118 (6): 3953–3960. Bibcode:2005ASAJ..118.3953C. doi:10.1121/1.2109167. PMID 16419839.
- Geisler, W.S.; Perry, J.S. (2011). "Statistics for optimal point prediction in natural images". Journal of Vision. 11 (12): 14. doi:10.1167/11.12.14. PMC 5144165. PMID 22011382.
- Cheung, V.; Frey, B. J.; Jojic, N. (20–25 June 2005). Video epitomes (PDF). Conference on Computer Vision and Pattern Recognition (CVPR). Vol. 1. pp. 42–49. doi:10.1109/CVPR.2005.366.
- Bertero, M.; Boccacci, P. (October 2003). "Super-resolution in computational imaging". Micron. 34 (6–7): 265–273. doi:10.1016/s0968-4328(03)00051-9. PMID 12932769.
- Borman, S.; Stevenson, R. (1998). "Spatial Resolution Enhancement of Low-Resolution Image Sequences – A Comprehensive Review with Directions for Future Research" (Technical report). University of Notre Dame.
- Borman, S.; Stevenson, R. (1998). Super-resolution from image sequences — a review (PDF). Midwest Symposium on Circuits and Systems.
- Park, S. C.; Park, M. K.; Kang, M. G. (May 2003). "Super-resolution image reconstruction: a technical overview". IEEE Signal Processing Magazine. 20 (3): 21–36. Bibcode:2003ISPM...20...21P. doi:10.1109/MSP.2003.1203207. S2CID 12320918.
- Farsiu, S.; Robinson, D.; Elad, M.; Milanfar, P. (August 2004). "Advances and Challenges in Super-Resolution". International Journal of Imaging Systems and Technology. 14 (2): 47–57. doi:10.1002/ima.20007. S2CID 12351561.
- Elad, M.; Hel-Or, Y. (August 2001). "Fast Super-Resolution Reconstruction Algorithm for Pure Translational Motion and Common Space-Invariant Blur". IEEE Transactions on Image Processing. 10 (8): 1187–1193. Bibcode:2001ITIP...10.1187E. CiteSeerX 10.1.1.11.2502. doi:10.1109/83.935034. PMID 18255535.
- Irani, M.; Peleg, S. (June 1990). Super Resolution From Image Sequences (PDF). International Conference on Pattern Recognition. Vol. 2. pp. 115–120.
- Sroubek, F.; Cristobal, G.; Flusser, J. (2007). "A Unified Approach to Superresolution and Multichannel Blind Deconvolution". IEEE Transactions on Image Processing. 16 (9): 2322–2332. Bibcode:2007ITIP...16.2322S. doi:10.1109/TIP.2007.903256. PMID 17784605. S2CID 6367149.
- Calabuig, Alejandro; Micó, Vicente; Garcia, Javier; Zalevsky, Zeev; Ferreira, Carlos (March 2011). "Single-exposure super-resolved interferometric microscopy by red–green–blue multiplexing". Optics Letters. 36 (6): 885–887. Bibcode:2011OptL...36..885C. doi:10.1364/OL.36.000885. PMID 21403717.
- Chan, Wai-San; Lam, Edmund; Ng, Michael K.; Mak, Giuseppe Y. (September 2007). "Super-resolution reconstruction in a computational compound-eye imaging system". Multidimensional Systems and Signal Processing. 18 (2–3): 83–101. doi:10.1007/s11045-007-0022-3. S2CID 16452552.
- Ng, Michael K.; Shen, Huanfeng; Lam, Edmund Y.; Zhang, Liangpei (2007). "A Total Variation Regularization Based Super-Resolution Reconstruction Algorithm for Digital Video". EURASIP Journal on Advances in Signal Processing. 2007: 074585. Bibcode:2007EJASP2007..104N. doi:10.1155/2007/74585. hdl:10722/73871.
- Glasner, D.; Bagon, S.; Irani, M. (October 2009). Super-Resolution from a Single Image (PDF). International Conference on Computer Vision (ICCV).; "example and results".
- Ben-Ezra, M.; Lin, Zhouchen; Wilburn, B.; Zhang, Wei (July 2011). "Penrose Pixels for Super-Resolution" (PDF). IEEE Transactions on Pattern Analysis and Machine Intelligence. 33 (7): 1370–1383. CiteSeerX 10.1.1.174.8804. doi:10.1109/TPAMI.2010.213. PMID 21135446. S2CID 184868.
- Berliner, L.; Buffa, A. (2011). "Super-resolution variable-dose imaging in digital radiography: quality and dose reduction with a fluoroscopic flat-panel detector". Int J Comput Assist Radiol Surg. 6 (5): 663–673. doi:10.1007/s11548-011-0545-9. PMID 21298404.
- Timofte, R.; De Smet, V.; Van Gool, L. (November 2014). A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution (PDF). 12th Asian Conference on Computer Vision (ACCV).; "codes and data".
- Huang, J.-B; Singh, A.; Ahuja, N. (June 2015). Single Image Super-Resolution from Transformed Self-Exemplars. IEEE Conference on Computer Vision and Pattern Recognition.; "project page".
- CHRISTENSEN-JEFFRIES, T.; COUTURE, O.; DAYTON, P.A.; ELDAR, Y.C.; HYNYNEN, K.; KIESSLING, F.; O’REILLY, M.; PINTON, G.F.; SCHMITZ, G.; TANG, M.-X.; TANTER, M.; VAN SLOUN, R.J.G. (2020). "Super-resolution Ultrasound Imaging". Ultrasound Med. Biol. 46 (4): 865–891. doi:10.1016/j.ultrasmedbio.2019.11.013. PMC 8388823. PMID 31973952.

