Volt-ampere
This article may be too technical for most readers to understand. (December 2019) |
| volt-ampere | |
|---|---|
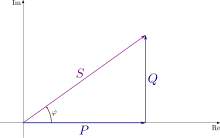 Apparent power () is the magnitude of the vector sum of real power vector () and reactive power vector (); is the phase shift between voltage and current. | |
| General information | |
| Unit system | SI units |
| Unit of | Apparent power |
| Symbol | V⋅A |
| Conversions | |
| 1 V⋅A in ... | ... is equal to ... |
| SI base units | 1 kg⋅m2⋅s−3 |
The volt-ampere (SI symbol: VA,[1] sometimes V⋅A or V A) is the unit of measurement for apparent power in an electrical circuit. It is the product of the root mean square voltage (in volts) and the root mean square current (in amperes).[2] Volt-amperes are usually used for analyzing alternating current (AC) circuits. In direct current (DC) circuits, this product is equal to the real power, measured in watts.[3] The volt-ampere is dimensionally equivalent to the watt: in SI units, 1 V⋅A = 1 W. VA rating is most used for generators and transformers, and other power handling equipment, where loads may be reactive (inductive or capacitive).
Formulation[edit]
For a simple electrical circuit running on direct current, the electrical current and voltage are constant. In that case, the real power (P, measured in watts) is the product of the current (I, measured in amperes) and the voltage from one side of the circuit to the other (V, measured in volts):
For alternating current, both the voltage and current are oscillating. Instantaneous power is still the product of instantaneous current and instantaneous voltage, but if both of those are ideal sine waves driving a purely resistive load (like an incandescent light bulb), average power becomes (with subscripts designating average (av), peak amplitude (pk) and root mean square (rms)):
More generally, when voltage and current are not in phase, these products no longer represent average power but a new apparent power (S), measured in volt-amperes:
Usage[edit]
The relationship between real power and apparent power is described by the power factor. With a purely resistive load, they are the same: the apparent power is equal to the real power. Where a reactive (capacitive or inductive) component is present in the load, the apparent power is greater than the real power as voltage and current are no longer in phase. In the limiting case of a purely reactive load, current is drawn but no power is dissipated in the load.
Some devices, including uninterruptible power supplies (UPSs), have ratings both for maximum volt-amperes and maximum watts. A common prefixed derived unit is "kilovolt-ampere" (symbol kVA). The VA rating is limited by the maximum permissible current, and the watt rating by the power-handling capacity of the device. When a UPS powers equipment which presents a reactive load with a low power factor, neither limit may safely be exceeded.[4] For example, a (large) UPS system rated to deliver 400,000 volt-amperes (400 kVA) at 220 volts can deliver a current of 1818 amperes (these are RMS values).
VA ratings are also often used for transformers; maximum output current is then VA rating divided by nominal output voltage.[5] Transformers with the same sized core usually have the same VA rating.
The convention of using the volt-ampere to distinguish apparent power from real power is allowed by the SI standard.[6][page needed]
Volt-ampere reactive [edit]
In electric power transmission and distribution, volt-ampere reactive (var) is a unit of measurement of reactive power. Reactive power exists in an AC circuit when the current and voltage are not in phase. The term var was proposed by the Romanian electrical engineer Constantin Budeanu and introduced in 1930 by the IEC in Stockholm, which has adopted it as the unit for reactive power.
Special instruments called varmeters are available to measure the reactive power in a circuit.[7]
The unit "var" is allowed by the International System of Units (SI) even though the unit var is representative of a form of power.[8] Per EU directive 80/181/EEC (the "metric directive"), the correct symbol is lower-case "var",[1] although the spellings "Var" and "VAr" are commonly seen, and "VAR" is widely used throughout the power industry.
References[edit]
- ^ a b Council Directive on units of measurements 80/181/EEC Chapter 1.2.3., p. 6: "Special names for the unit of power: the name volt–ampere (symbol ‘VA’) when it is used to express the apparent power of alternating electric current, and var (symbol ‘var’) when it is used to express reactive electric power."
- ^ Ciletti, M. D., Irwin, J. D., Kraus, A. D., Balabanian, N., Bickard, T. A., and Chan, S. P. (1993). Linear circuit analysis. In Electrical Engineering Handbook, edited by R. C. Dorf. Boca Raton: CRC Press. (pp.82–87)
- ^ IEEE 100 : the authoritative dictionary of IEEE standards terms.-7th ed. ISBN 0-7381-2601-2, page 14
- ^ Watt Ratings Differs from Volt Amp Ratings APC
- ^ "Transformers and VA Ratings". 2012-06-27. Retrieved 13 December 2016.
- ^ "SI Brochure" (PDF) (8th ed.). Archived from the original on March 29, 2019.
- ^ Wildi, Theodore (2002). Electrical Machines, Drives and Power Systems. Pearson. p. 137. ISBN 978-0-13-093083-5.
- ^ SI Brochure, 8th ed.
 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.
This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on 2022-01-22.







