Waveguide

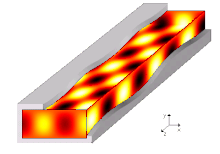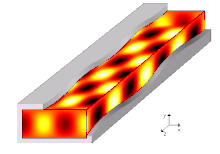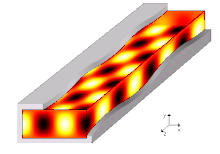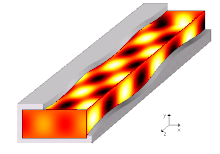
A waveguide is a structure that guides waves by restricting the transmission of energy to one direction. Common types of waveguides include acoustic waveguides which direct sound, optical waveguides which direct light, and radio-frequency waveguides which direct electromagnetic waves other than light like radio waves.
Without the physical constraint of a waveguide, waves would expand into three-dimensional space and their intensities would decrease according to the inverse square law.
There are different types of waveguides for different types of waves. The original and most common meaning is a hollow conductive metal pipe used to carry high frequency radio waves, particularly microwaves.[1] Dielectric waveguides are used at higher radio frequencies, and transparent dielectric waveguides and optical fibers serve as waveguides for light. In acoustics, air ducts and horns are used as waveguides for sound in musical instruments and loudspeakers, and specially-shaped metal rods conduct ultrasonic waves in ultrasonic machining.
The geometry of a waveguide reflects its function; in addition to more common types that channel the wave in one dimension, there are two-dimensional slab waveguides which confine waves to two dimensions. The frequency of the transmitted wave also dictates the size of a waveguide: each waveguide has a cutoff wavelength determined by its size and will not conduct waves of greater wavelength; an optical fiber that guides light will not transmit microwaves which have a much larger wavelength. Some naturally occurring structures can also act as waveguides. The SOFAR channel layer in the ocean can guide the sound of whale song across enormous distances.[2] Any shape of cross section of waveguide can support EM waves. Irregular shapes are difficult to analyse. Commonly used waveguides are rectangular and circular in shape.
Uses
[edit]
The uses of waveguides for transmitting signals were known even before the term was coined. The phenomenon of sound waves guided through a taut wire have been known for a long time, as well as sound through a hollow pipe such as a cave or medical stethoscope. Other uses of waveguides are in transmitting power between the components of a system such as radio, radar or optical devices. Waveguides are the fundamental principle of guided wave testing (GWT), one of the many methods of non-destructive evaluation.[3]
Specific examples:
- Optical fibers transmit light and signals for long distances with low attenuation and a wide usable range of wavelengths.
- In a microwave oven a waveguide transfers power from the magnetron, where waves are formed, to the cooking chamber.
- In a radar, a waveguide transfers radio frequency energy to and from the antenna, where the impedance needs to be matched for efficient power transmission (see below).
- Rectangular and circular waveguides are commonly used to connect feeds of parabolic dishes to their electronics, either low-noise receivers or power amplifier/transmitters.
- Waveguides are used in scientific instruments to measure optical, acoustic and elastic properties of materials and objects. The waveguide can be put in contact with the specimen (as in a medical ultrasonography), in which case the waveguide ensures that the power of the testing wave is conserved, or the specimen may be put inside the waveguide (as in a dielectric constant measurement, so that smaller objects can be tested and the accuracy is better.[4]
- A transmission line is a commonly used specific type of waveguide.[5]
History
[edit]This section duplicates the scope of other articles, specifically Waveguide (electromagnetism)#History. (November 2020) |
The first structure for guiding waves was proposed by J. J. Thomson in 1893, and was first experimentally tested by Oliver Lodge in 1894. The first mathematical analysis of electromagnetic waves in a metal cylinder was performed by Lord Rayleigh in 1897.[6]: 8 For sound waves, Lord Rayleigh published a full mathematical analysis of propagation modes in his seminal work, "The Theory of Sound".[7] Jagadish Chandra Bose researched millimeter wavelengths using waveguides, and in 1897 described to the Royal Institution in London his research carried out in Kolkata.[8][9]
The study of dielectric waveguides (such as optical fibers, see below) began as early as the 1920s, by several people, most famous of which are Rayleigh, Sommerfeld and Debye.[10] Optical fiber began to receive special attention in the 1960s due to its importance to the communications industry.
The development of radio communication initially occurred at the lower frequencies because these could be more easily propagated over large distances. The long wavelengths made these frequencies unsuitable for use in hollow metal waveguides because of the impractically large diameter tubes required. Consequently, research into hollow metal waveguides stalled and the work of Lord Rayleigh was forgotten for a time and had to be rediscovered by others. Practical investigations resumed in the 1930s by George C. Southworth at Bell Labs and Wilmer L. Barrow at MIT. Southworth at first took the theory from papers on waves in dielectric rods because the work of Lord Rayleigh was unknown to him. This misled him somewhat; some of his experiments failed because he was not aware of the phenomenon of waveguide cutoff frequency already found in Lord Rayleigh's work. Serious theoretical work was taken up by John R. Carson and Sallie P. Mead. This work led to the discovery that for the TE01 mode in circular waveguide losses go down with frequency and at one time this was a serious contender for the format for long-distance telecommunications.[11]: 544–548
The importance of radar in World War II gave a great impetus to waveguide research, at least on the Allied side. The magnetron, developed in 1940 by John Randall and Harry Boot at the University of Birmingham in the United Kingdom, provided a good power source and made microwave radar feasible. The most important centre of US research was at the Radiation Laboratory (Rad Lab) at MIT but many others took part in the US, and in the UK such as the Telecommunications Research Establishment. The head of the Fundamental Development Group at Rad Lab was Edward Mills Purcell. His researchers included Julian Schwinger, Nathan Marcuvitz, Carol Gray Montgomery, and Robert H. Dicke. Much of the Rad Lab work concentrated on finding lumped element models of waveguide structures so that components in waveguide could be analysed with standard circuit theory. Hans Bethe was also briefly at Rad Lab, but while there he produced his small aperture theory which proved important for waveguide cavity filters, first developed at Rad Lab. The German side, on the other hand, largely ignored the potential of waveguides in radar until very late in the war. So much so that when radar parts from a downed British plane were sent to Siemens & Halske for analysis, even though they were recognised as microwave components, their purpose could not be identified.
At that time, microwave techniques were badly neglected in Germany. It was generally believed that it was of no use for electronic warfare, and those who wanted to do research work in this field were not allowed to do so.
— H. Mayer, wartime vice-president of Siemens & Halske
German academics were even allowed to continue publicly publishing their research in this field because it was not felt to be important.[12]: 548–554 [13]: 1055, 1057
Immediately after World War II waveguide was the technology of choice in the microwave field. However, it has some problems; it is bulky, expensive to produce, and the cutoff frequency effect makes it difficult to produce wideband devices. Ridged waveguide can increase bandwidth beyond an octave, but a better solution is to use a technology working in TEM mode (that is, non-waveguide) such as coaxial conductors since TEM does not have a cutoff frequency. A shielded rectangular conductor can also be used and this has certain manufacturing advantages over coax and can be seen as the forerunner of the planar technologies (stripline and microstrip). However, planar technologies really started to take off when printed circuits were introduced. These methods are significantly cheaper than waveguide and have largely taken its place in most bands. However, waveguide is still favoured in the higher microwave bands from around Ku band upwards.[12]: 556–557 [14]: 21–27, 21–50
Properties
[edit]Propagation modes and cutoff frequencies
[edit]A propagation mode in a waveguide is one solution of the wave equations, or, in other words, the form of the wave.[10] Due to the constraints of the boundary conditions, there are only limited frequencies and forms for the wave function which can propagate in the waveguide. The lowest frequency in which a certain mode can propagate is the cutoff frequency of that mode. The mode with the lowest cutoff frequency is the fundamental mode of the waveguide, and its cutoff frequency is the waveguide cutoff frequency.[15]: 38
Propagation modes are computed by solving the Helmholtz equation alongside a set of boundary conditions depending on the geometrical shape and materials bounding the region. The usual assumption for infinitely long uniform waveguides allows us to assume a propagating form for the wave, i.e. stating that every field component has a known dependency on the propagation direction (i.e. ). More specifically, the common approach is to first replace all unknown time-varying fields (assuming for simplicity to describe the fields in cartesian components) with their complex phasors representation , sufficient to fully describe any infinitely long single-tone signal at frequency , (angular frequency ), and rewrite the Helmholtz equation and boundary conditions accordingly. Then, every unknown field is forced to have a form like , where the term represents the propagation constant (still unknown) along the direction along which the waveguide extends to infinity. The Helmholtz equation can be rewritten to accommodate such form and the resulting equality needs to be solved for and , yielding in the end an eigenvalue equation for and a corresponding eigenfunction for each solution of the former.[16]
The propagation constant of the guided wave is complex, in general. For a lossless case, the propagation constant might be found to take on either real or imaginary values, depending on the chosen solution of the eigenvalue equation and on the angular frequency . When is purely real, the mode is said to be "below cutoff", since the amplitude of the field phasors tends to exponentially decrease with propagation; an imaginary , instead, represents modes said to be "in propagation" or "above cutoff", as the complex amplitude of the phasors does not change with .[17]
Impedance matching
[edit]In circuit theory, the impedance is a generalization of electrical resistance in the case of alternating current, and is measured in ohms ().[10] A waveguide in circuit theory is described by a transmission line having a length and characteristic impedance.[18]: 2–3, 6–12 [19]: 14 [20] In other words, the impedance indicates the ratio of voltage to current of the circuit component (in this case a waveguide) during propagation of the wave. This description of the waveguide was originally intended for alternating current, but is also suitable for electromagnetic and sound waves, once the wave and material properties (such as pressure, density, dielectric constant) are properly converted into electrical terms (current and impedance for example).[21]: 14
Impedance matching is important when components of an electric circuit are connected (waveguide to antenna for example): The impedance ratio determines how much of the wave is transmitted forward and how much is reflected. In connecting a waveguide to an antenna a complete transmission is usually required, so an effort is made to match their impedances.[20]
The reflection coefficient can be calculated using: , where (Gamma) is the reflection coefficient (0 denotes full transmission, 1 full reflection, and 0.5 is a reflection of half the incoming voltage), and are the impedance of the first component (from which the wave enters) and the second component, respectively.[22]
An impedance mismatch creates a reflected wave, which added to the incoming waves creates a standing wave. An impedance mismatch can be also quantified with the standing wave ratio (SWR or VSWR for voltage), which is connected to the impedance ratio and reflection coefficient by: , where are the minimum and maximum values of the voltage absolute value, and the VSWR is the voltage standing wave ratio, which value of 1 denotes full transmission, without reflection and thus no standing wave, while very large values mean high reflection and standing wave pattern.[20]
Electromagnetic waveguides
[edit]Radio-frequency waveguides
[edit]Waveguides can be constructed to carry waves over a wide portion of the electromagnetic spectrum, but are especially useful in the microwave and optical frequency ranges. Depending on the frequency, they can be constructed from either conductive or dielectric materials. Waveguides are used for transferring both power and communication signals.[15]: 1–3 [23]: xiii–xiv

Optical waveguides
[edit]Waveguides used at optical frequencies are typically dielectric waveguides, structures in which a dielectric material with high permittivity, and thus high index of refraction, is surrounded by a material with lower permittivity. The structure guides optical waves by total internal reflection. An example of an optical waveguide is optical fiber.[24]
Other types of optical waveguide are also used, including photonic-crystal fiber, which guides waves by any of several distinct mechanisms. Guides in the form of a hollow tube with a highly reflective inner surface have also been used as light pipes for illumination applications. The inner surfaces may be polished metal, or may be covered with a multilayer film that guides light by Bragg reflection (this is a special case of a photonic-crystal fiber). One can also use small prisms around the pipe which reflect light via total internal reflection [1]—such confinement is necessarily imperfect, however, since total internal reflection can never truly guide light within a lower-index core (in the prism case, some light leaks out at the prism corners).[25]
Acoustic waveguides
[edit]An acoustic waveguide is a physical structure for guiding sound waves. Sound in an acoustic waveguide behaves like electromagnetic waves on a transmission line. Waves on a string, like the ones in a tin can telephone, are a simple example of an acoustic waveguide. Another example are pressure waves in the pipes of an organ. The term acoustic waveguide is also used to describe elastic waves guided in micro-scale devices, like those employed in piezoelectric delay lines and in stimulated Brillouin scattering.
Mathematical waveguides
[edit]Waveguides are interesting objects of study from a strictly mathematical perspective. A waveguide (or tube) is defined as type of boundary condition on the wave equation such that the wave function must be equal to zero on the boundary and that the allowed region is finite in all dimensions but one (an infinitely long cylinder is an example.) A large number of interesting results can be proven from these general conditions. It turns out that any tube with a bulge (where the width of the tube increases) admits at least one bound state that exist inside the mode gaps. The frequencies of all the bound states can be identified by using a pulse short in time. This can be shown using the variational principles. An interesting result by Jeffrey Goldstone and Robert Jaffe is that any tube of constant width with a twist, admits a bound state.[26]
Sound synthesis
[edit]Sound synthesis uses digital delay lines as computational elements to simulate wave propagation in tubes of wind instruments and the vibrating strings of string instruments.[27]
See also
[edit]- Circular polarization
- Earth–ionosphere waveguide
- Linear polarization
- Orthomode transducer
- Polarization
- Flap attenuator
Notes
[edit]- ^ Institute of Electrical and Electronics et al. 1997.
- ^ Payne & Webb 1971.
- ^ Olisa, Khan & Starr 2021.
- ^ Baker-Jarvis 1990.
- ^ EETech Media.
- ^ McLachlan 1964.
- ^ Rayleigh 1894.
- ^ Emerson 1997a.
- ^ Emerson 1997b, Reprint.
- ^ a b c Balanis 1989.
- ^ Oliner 2006, Reprint.
- ^ a b Oliner 2006.
- ^ Levy & Cohn 1984.
- ^ Han & Hwang 2012.
- ^ a b Cronin 1995.
- ^ Pozar 2012.
- ^ Ramo, Whinnery & Van Duzer 1994.
- ^ Marcuvitz 1951.
- ^ Beranek & Mellow 2012, Characteristic Impedance.
- ^ a b c Khare & Nema 2012.
- ^ Beranek & Mellow 2012, Pressure and density effects.
- ^ Zhang, Krooswyk & Ou 2015, Reflection coefficient.
- ^ Okamoto 2010.
- ^ Herres.
- ^ Saxe 1989.
- ^ Goldstone & Jaffe 1992.
- ^ Smith 1996.
References
[edit]- Baker-Jarvis, James (1990). Transmission/Reflection and short-Circuit Line Permittivity Measurements (PDF). Boulder, Colorado: National Institute of Standards and Technology.
- Balanis, Constantine A. (1989). Engineering Electromagnetics. Wiley. ISBN 978-0-471-62194-2. Archived from the original on May 14, 2009.
- Beranek, Leo Leroy; Mellow, Tim (2012). Acoustics: Sound Fields and Transducers. Academic Press. ISBN 978-0-12-391421-7.
- Cronin, N. J. (1995). Microwave and Optical Waveguides. CRC Press. p. 38. ISBN 978-0-7503-0216-6.
- EETech Media, LLC. "Waveguides". All About Circuits. Retrieved December 31, 2023.
- Emerson, D.T. (1997). "The work of Jagadis Chandra Bose: 100 years of mm-wave research". 1997 IEEE MTT-S International Microwave Symposium Digest. Vol. 2. pp. 553–556. doi:10.1109/MWSYM.1997.602853. ISBN 0-7803-3814-6. S2CID 9039614.
- Emerson, D.T. (1997b). "The work of Jagadis Chandra Bose: 100 years of millimeter-wave research". IEEE Transactions on Microwave Theory and Techniques. 45 (12): 2267–2273. Bibcode:1997ITMTT..45.2267E. doi:10.1109/22.643830. ISBN 9780986488511.
- Goldstone, J.; Jaffe, R. L. (1992). "Bound states in twisting tubes". Physical Review B. 45 (24): 14100–14107. Bibcode:1992PhRvB..4514100G. doi:10.1103/PhysRevB.45.14100. PMID 10001530.
- Han, C.C.; Hwang, Y. (2012). "Satellite attenas". In Lo, Y. T.; Lee, S. W. (eds.). Antenna Handbook: Volume III Applications. Springer Science & Business Media. ISBN 978-1-4615-2638-4.
- Herres, David. "Optical Fiber: A waveguide for light and internal reflection". Test & Measurement Tips. Retrieved January 1, 2024.
- Institute of Electrical and Electronics, Engineers; Radatz, Jane; Standards Coordinating Committee, Terms and Definitions; IEEE Computer Society, Standards Coordinating Committee (1997). The IEEE Standard Dictionary of Electrical and Electronics Terms (6th ed.). New York, New York: Institute of Electrical and Electronics Engineers. ISBN 978-1-55937-833-8.
- Khare, Rashmi; Nema, Rajesh (2012). "Review of Impedance Matching Networks for Bandwidth Enhancement". International Journal of Emerging Technology and Advanced Engineering. 2 (1): 92–96.
- Levy, R.; Cohn, S.B. (1984). "A History of Microwave Filter Research, Design, and Development". IEEE Transactions on Microwave Theory and Techniques. 32 (9): 1055–1067. Bibcode:1984ITMTT..32.1055L. doi:10.1109/TMTT.1984.1132817.
- Lo, Y. T.; Lee, S. W. (December 6, 2012). Antenna Handbook: Volume III Applications. Springer Science & Business Media. ISBN 978-1-4615-2638-4.
- McLachlan, Norman William (1964). Theory and Application of Mathieu Functions, By N.W. Mclachlan. New York, New York: Dover.
- Marcuvitz, Nathan (1951). Waveguide Handbook. IET. ISBN 978-0-86341-058-1.
- Okamoto, Katsunari (2010). Fundamentals of Optical Waveguides. Elsevier. ISBN 978-0-08-045506-8.
- Oliner, Arthur A. (January 30, 2006). "The evolution of electromagnetic waveguides: from hollow metallic guides to microwave integrated circuits". In Sarkar, T. K.; Mailloux, Robert; Oliner, Arthur A.; Salazar-Palma, Magdalena; Sengupta, Dipak L. (eds.). History of Wireless. John Wiley & Sons. pp. 543–566. ISBN 978-0-471-78301-5.
- Olisa, Samuel Chukwuemeka; Khan, Muhammad A.; Starr, Andrew (2021). "Review of Current Guided Wave Ultrasonic Testing (GWUT) Limitations and Future Directions". Sensors. 21 (3): 811. Bibcode:2021Senso..21..811O. doi:10.3390/s21030811. PMC 7865912. PMID 33530407.
- Payne, R.; Webb, D. (1971). "Orientation by means of long range acoustic signaling in baleen whales". Annals of the New York Academy of Sciences. 188 (1): 110–141. Bibcode:1971NYASA.188..110P. doi:10.1111/j.1749-6632.1971.tb13093.x. ISSN 0077-8923. PMID 5288850. S2CID 42324742.
- Pozar, David M. (2012). Microwave Engineering. John Wiley & Sons. ISBN 978-0-470-63155-3.
- Ramo, Simon; Whinnery, John R.; Van Duzer, Theodore (1994). Fields and Waves in Communication Electronics. New York: John Wiley and Sons. pp. 321–324. ISBN 978-0-471-58551-0.
- Rayleigh, John William Strutt Baron (1894). The Theory of Sound. Macmillan.
- Saxe, Steven G. (1989). "Prismatic film light guides: Performance and recent developments". Solar Energy Materials. 19 (1): 95–109. doi:10.1016/0165-1633(89)90026-9. ISSN 0165-1633.
- Smith, Julius O. (1996). "Physical Modeling Synthesis Update". Computer Music Journal. 20 (2): 44–56. doi:10.2307/3681331. ISSN 0148-9267. JSTOR 3681331.
- Zhang, Hanqiao; Krooswyk, Steven; Ou, Jeff (2015). "Chapter 1 - Transmission line fundamentals". High Speed Digital Design. Morgan Kaufmann. pp. 1–26. ISBN 978-0-12-418663-7.
External links
[edit]- Electromagnetic Waves and Antennas: Waveguides Sophocles J. Orfanidis, Department of Electrical and Computer Engineering, Rutgers University

















