Cayley graph

The Cayley graph of the free group on two generators a and b

Graph families defined by their automorphisms
distance-transitive	→	distance-regular	←	strongly regular
↓
symmetric (arc-transitive)	←	t-transitive, t ≥ 2		skew-symmetric
↓
(if connected) vertex- and edge-transitive	→	edge-transitive and regular	→	edge-transitive
↓		↓		↓
vertex-transitive	→	regular	→	(if bipartite) biregular
↑
Cayley graph	←	zero-symmetric		asymmetric

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem (named after Arthur Cayley) and uses a specified, set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing families of expander graphs.

Definition

Let $G$ be a group and $S$ be a generating set of $G$. The Cayley graph $\Gamma =\Gamma (G,S)$ is an edge-colored directed graph constructed as follows:

• Each element $g$ of $G$ is assigned a vertex: the vertex set of $\Gamma$ is identified with $G.$
• Each element $s$ of $S$ is assigned a color $c_{s}$.
• For every $g\in G$ and $s\in S$, there is a directed edge of color $c_{s}$ from the vertex corresponding to $g$ to the one corresponding to $gs$.

Not every source requires that $S$ generate the group. If $S$ is not a generating set for $G$, then $\Gamma$ is disconnected and each connected component represents a coset of the subgroup generated by $S$.

If an element $s$ of $S$ is its own inverse, $s=s^{-1},$ then it is typically represented by an undirected edge.

The set $S$ is sometimes assumed to be symmetric (i.e. $S=S^{-1}$) and not containing the identity element of the group. In this case, the uncolored Cayley graph can be represented as a simple undirected graph.

In geometric group theory, the set $S$ is often assumed to be finite which corresponds to $\Gamma$ being locally finite.

Examples

• Suppose that $G=\mathbb {Z}$ is the infinite cyclic group and the set $S$ consists of the standard generator 1 and its inverse (−1 in the additive notation); then the Cayley graph is an infinite path.
• Similarly, if $G=\mathbb {Z} _{n}$ is the finite cyclic group of order $n$ and the set $S$ consists of two elements, the standard generator of $G$ and its inverse, then the Cayley graph is the cycle $C_{n}$. More generally, the Cayley graphs of finite cyclic groups are exactly the circulant graphs.
• The Cayley graph of the direct product of groups (with the cartesian product of generating sets as a generating set) is the cartesian product of the corresponding Cayley graphs. Thus the Cayley graph of the abelian group $\mathbb {Z} ^{2}$ with the set of generators consisting of four elements $(\pm 1,0),(0,\pm 1)$ is the infinite grid on the plane $\mathbb {R} ^{2}$, while for the direct product $\mathbb {Z} _{n}\times \mathbb {Z} _{m}$ with similar generators the Cayley graph is the $n\times m$ finite grid on a torus.

Cayley graph of the dihedral group $D_{4}$ on two generators a and b

Cayley graph of $D_{4}$, on two generators which are both self-inverse

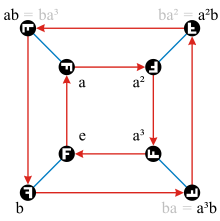
• A Cayley graph of the dihedral group $D_{4}$ on two generators $a$ and $b$ is depicted to the left. Red arrows represent composition with $a$. Since $b$ is self-inverse, the blue lines, which represent composition with $b$, are undirected. Therefore the graph is mixed: it has eight vertices, eight arrows, and four edges. The Cayley table of the group $D_{4}$ can be derived from the group presentation

$\langle a,b\mid a^{4}=b^{2}=e,ab=ba^{3}\rangle .$

A different Cayley graph of $D_{4}$ is shown on the right. $b$ is still the horizontal reflection and is represented by blue lines, and $c$ is a diagonal reflection and is represented by pink lines. As both reflections are self-inverse the Cayley graph on the right is completely undirected. This graph corresponds to the presentation

$\langle b,c\mid b^{2}=c^{2}=e,bcbc=cbcb\rangle .$

• The Cayley graph of the free group on two generators $a$ and $b$ corresponding to the set $S=\{a,b,a^{-1},b^{-1}\}$ is depicted at the top of the article, and $e$ represents the identity element. Travelling along an edge to the right represents right multiplication by $a,$ while travelling along an edge upward corresponds to the multiplication by $b.$ Since the free group has no relations, the Cayley graph has no cycles. This Cayley graph is a 4-regular infinite tree and is a key ingredient in the proof of the Banach–Tarski paradox.

Part of a Cayley graph of the Heisenberg group. (The coloring is only for visual aid.)

• A Cayley graph of the discrete Heisenberg group

$\left\{{\begin{pmatrix}1&x&z\\0&1&y\\0&0&1\\\end{pmatrix}},\ x,y,z\in \mathbb {Z} \right\}$

is depicted to the right. The generators used in the picture are the three matrices $X,Y,Z$ given by the three permutations of 1, 0, 0 for the entries $x,y,z$. They satisfy the relations $Z=XYX^{-1}Y^{-1},XZ=ZX,YZ=ZY$, which can also be understood from the picture. This is a non-commutative infinite group, and despite being a three-dimensional space, the Cayley graph has four-dimensional volume growth.

Cayley Q8 graph showing cycles of multiplication by quaternions i, j and k

Characterization

The group $G$ acts on itself by left multiplication (see Cayley's theorem). This may be viewed as the action of $G$ on its Cayley graph. Explicitly, an element $h\in G$ maps a vertex $g\in V(\Gamma )$ to the vertex $hg\in V(\Gamma ).$ The set of edges of the Cayley graph and their color is preserved by this action: the edge $(g,gs)$ is mapped to the edge $(hg,hgs)$, both having color $c_{s}$. The left multiplication action of a group on itself is simply transitive, in particular, Cayley graphs are vertex-transitive. The following is a kind of converse to this:

Sabidussi's Theorem. An (unlabeled and uncolored) directed graph $\Gamma$ is a Cayley graph of a group $G$ if and only if it admits a simply transitive action of $G$ by graph automorphisms (i.e. preserving the set of directed edges).

To recover the group $G$ and the generating set $S$ from the unlabeled directed graph $\Gamma ,$ select a vertex $v_{1}\in V(\Gamma )$ and label it by the identity element of the group. Then label each vertex $v$ of $\Gamma$ by the unique element of $G$ that maps $v_{1}$ to $v.$ The set $S$ of generators of $G$ that yields $\Gamma$ as the Cayley graph $\Gamma (G,S)$ is the set of labels of out-neighbors of $v_{1}$.

Elementary properties

• The Cayley graph $\Gamma (G,S)$ depends in an essential way on the choice of the set $S$ of generators. For example, if the generating set $S$ has $k$ elements then each vertex of the Cayley graph has $k$ incoming and $k$ outgoing directed edges. In the case of a symmetric generating set $S$ with $r$ elements, the Cayley graph is a regular directed graph of degree $r.$
• Cycles (or closed walks) in the Cayley graph indicate relations between the elements of $S.$ In the more elaborate construction of the Cayley complex of a group, closed paths corresponding to relations are "filled in" by polygons. This means that the problem of constructing the Cayley graph of a given presentation ${\mathcal {P}}$ is equivalent to solving the Word Problem for ${\mathcal {P}}$.
• If $f:G'\to G$ is a surjective group homomorphism and the images of the elements of the generating set $S'$ for $G'$ are distinct, then it induces a covering of graphs

${\bar {f}}:\Gamma (G',S')\to \Gamma (G,S),$

where $S=f(S').$ In particular, if a group $G$ has $k$ generators, all of order different from 2, and the set $S$ consists of these generators together with their inverses, then the Cayley graph $\Gamma (G,S)$ is covered by the infinite regular tree of degree $2k$ corresponding to the free group on the same set of generators.

• For any finite Cayley graph, considered as undirected, the vertex connectivity is at least equal to 2/3 of the degree of the graph. If the generating set is minimal (removal of any element and, if present, its inverse from the generating set leaves a set which is not generating), the vertex connectivity is equal to the degree. The edge connectivity is in all cases equal to the degree.
• If $\rho _{\text{reg}}(g)(x)=gx$ is the left-regular representation with $|G|\times |G|$ matrix form denoted $[\rho _{\text{reg}}(g)]$, the adjacency matrix of $\Gamma (G,S)$ is $A=\sum _{s\in S}[\rho _{\text{reg}}(g)]$.
• Every group character $\chi$ of the group $G$ induces an eigenvector of the adjacency matrix of $\Gamma (G,S)$. When $G$ is Abelian, the associated eigenvalue is

$\lambda _{\chi }=\sum _{s\in S}\chi (s),$ which takes the form $\sum _{s\in S}e^{2\pi ijs/|G|}$ for integers $j=0,1,\dots ,|G|-1.$

In particular, the associated eigenvalue of the trivial character (the one sending every element to 1) is the degree of $\Gamma (G,S)$, that is, the order of $S$. If $G$ is an Abelian group, there are exactly $|G|$ characters, determining all eigenvalues. The corresponding orthonormal basis of eigenvectors is given by $v_{j}={\tfrac {1}{\sqrt {|G|}}}{\begin{pmatrix}1&e^{2\pi ij/|G|}&e^{2\cdot 2\pi ij/|G|}&e^{3\cdot 2\pi ij/|G|}&\cdots &e^{(|G|-1)2\pi ij/|G|}\end{pmatrix}}.$ It is interesting to note that this eigenbasis is independent of the generating set $S$.

More generally for symmetric generating sets, take $\rho _{1},\dots ,\rho _{k}$ a complete set of irreducible representations of $G,$ and let $\rho _{i}(S)=\sum _{s\in S}\rho _{i}(s)$ with eigenvalue set $\Lambda _{i}(S)$. Then the set of eigenvalues of $\Gamma (G,S)$ is exactly $\bigcup _{i}\Lambda _{i}(S),$ where eigenvalue $\lambda$ appears with multiplicity $\dim(\rho _{i})$ for each occurrence of $\lambda$ as an eigenvalue of $\rho _{i}(S).$

Schreier coset graph

Main article: Schreier coset graph

If one, instead, takes the vertices to be right cosets of a fixed subgroup $H,$ one obtains a related construction, the Schreier coset graph, which is at the basis of coset enumeration or the Todd–Coxeter process.

Connection to group theory

Knowledge about the structure of the group can be obtained by studying the adjacency matrix of the graph and in particular applying the theorems of spectral graph theory. Conversely, for symmetric generating sets, the spectral and representation theory of $\Gamma (G,S)$ are directly tied together: take $\rho _{1},\dots ,\rho _{k}$ a complete set of irreducible representations of $G,$ and let $\rho _{i}(S)=\sum _{s\in S}\rho _{i}(s)$ with eigenvalues $\Lambda _{i}(S)$. Then the set of eigenvalues of $\Gamma (G,S)$ is exactly $\bigcup _{i}\Lambda _{i}(S),$ where eigenvalue $\lambda$ appears with multiplicity $\dim(\rho _{i})$ for each occurrence of $\lambda$ as an eigenvalue of $\rho _{i}(S).$

The genus of a group is the minimum genus for any Cayley graph of that group.

Geometric group theory

For infinite groups, the coarse geometry of the Cayley graph is fundamental to geometric group theory. For a finitely generated group, this is independent of choice of finite set of generators, hence an intrinsic property of the group. This is only interesting for infinite groups: every finite group is coarsely equivalent to a point (or the trivial group), since one can choose as finite set of generators the entire group.

Formally, for a given choice of generators, one has the word metric (the natural distance on the Cayley graph), which determines a metric space. The coarse equivalence class of this space is an invariant of the group.

Expansion properties

When $S=S^{-1}$, the Cayley graph $\Gamma (G,S)$ is $|S|$-regular, so spectral techniques may be used to analyze the expansion properties of the graph. In particular for abelian groups, the eigenvalues of the Cayley graph are more easily computable and given by $\lambda _{\chi }=\sum _{s\in S}\chi (s)$ with top eigenvalue equal to $|S|$, so we may use Cheeger's inequality to bound the edge expansion ratio using the spectral gap.

Representation theory can be used to construct such expanding Cayley graphs, in the form of Kazhdan property (T). The following statement holds:

If a discrete group $G$ has Kazhdan's property (T), and $S$ is a finite, symmetric generating set of $G$, then there exists a constant $c>0$ depending only on $G,S$ such that for any finite quotient $Q$ of $G$ the Cayley graph of $Q$ with respect to the image of $S$ is a $c$-expander.

For example the group $G=\mathrm {SL} _{3}(\mathbb {Z} )$ has property (T) and is generated by elementary matrices and this gives relatively explicit examples of expander graphs.

Integral classification

An integral graph is one whose eigenvalues are all integers. While the complete classification of integral graphs remains an open problem, the Cayley graphs of certain groups are always integral. Using previous characterizations of the spectrum of Cayley graphs, note that $\Gamma (G,S)$ is integral iff the eigenvalues of $\rho (S)$ are integral for every representation $\rho$ of $G$.

Cayley integral simple group

A group $G$ is Cayley integral simple (CIS) if the connected Cayley graph $\Gamma (G,S)$ is integral exactly when the symmetric generating set $S$ is the complement of a subgroup of $G$. A result of Ahmady, Bell, and Mohar shows that all CIS groups are isomorphic to $\mathbb {Z} /p\mathbb {Z} ,\mathbb {Z} /p^{2}\mathbb {Z}$, or $\mathbb {Z} _{2}\times \mathbb {Z} _{2}$ for primes $p$. It is important that $S$ actually generates the entire group $G$ in order for the Cayley graph to be connected. (If $S$ does not generate $G$, the Cayley graph may still be integral, but the complement of $S$ is not necessarily a subgroup.)

In the example of $G=\mathbb {Z} /5\mathbb {Z}$, the symmetric generating sets (up to graph isomorphism) are

• $S=\{1,4\}$: $\Gamma (G,S)$ is a $5$-cycle with eigenvalues $2,{\tfrac {{\sqrt {5}}-1}{2}},{\tfrac {{\sqrt {5}}-1}{2}},{\tfrac {-{\sqrt {5}}-1}{2}},{\tfrac {-{\sqrt {5}}-1}{2}}$
• $S=\{1,2,3,4\}$: $\Gamma (G,S)$ is $K_{5}$ with eigenvalues $4,-1,-1,-1,-1$

The only subgroups of $\mathbb {Z} /5\mathbb {Z}$ are the whole group and the trivial group, and the only symmetric generating set $S$ that produces an integral graph is the complement of the trivial group. Therefore $\mathbb {Z} /5\mathbb {Z}$ must be a CIS group.

The proof of the complete CIS classification uses the fact that every subgroup and homomorphic image of a CIS group is also a CIS group.

Cayley integral group

A slightly different notion is that of a Cayley integral group $G$, in which every symmetric subset $S$ produces an integral graph $\Gamma (G,S)$. Note that $S$ no longer has to generate the entire group.

The complete list of Cayley integral groups is given by $\mathbb {Z} _{2}^{n}\times \mathbb {Z} _{3}^{m},\mathbb {Z} _{2}^{n}\times \mathbb {Z} _{4}^{n},Q_{8}\times \mathbb {Z} _{2}^{n},S_{3}$, and the dicyclic group of order $12$, where $m,n\in \mathbb {Z} _{\geq 0}$ and $Q_{8}$ is the quaternion group. The proof relies on two important properties of Cayley integral groups:

• Subgroups and homomorphic images of Cayley integral groups are also Cayley integral groups.
• A group is Cayley integral iff every connected Cayley graph of the group is also integral.

Normal and Eulerian generating sets

Given a general group $G$, $S\subseteq G$ is normal if $S$ is closed under conjugation by elements of $G$ (generalizing the notion of a normal subgroup), and $S$ is Eulerian if for every $s\in S$, the set of elements generating the cyclic group $\langle s\rangle$ is also contained in $S$. A 2019 result by Guo, Lytkina, Mazurov, and Revin proves that the Cayley graph $\Gamma (G,S)$ is integral for any Eulerian normal subset $S\subseteq G$, using purely representation theoretic techniques.

The proof of this result is relatively short: given $S$ an Eulerian normal subset, select $x_{1},\dots ,x_{t}\in G$ pairwise nonconjugate so that $S$ is the union of the conjugacy classes $\operatorname {Cl} (x_{i})$. Then using the characterization of the spectrum of a Cayley graph, one can show the eigenvalues of $\Gamma (G,S)$ are given by $\left\{\lambda _{\chi }=\sum _{i=1}^{t}{\frac {\chi (x_{i})|\operatorname {Cl} (x_{i})|}{\chi (1)}}\right\}$ taken over irreducible characters $\chi$ of $G$. Each eigenvalue $\lambda _{\chi }$ in this set must be an element of $\mathbb {Q} (\zeta )$ for $\zeta$ a primitive $m^{th}$ root of unity (where $m$ must be divisible by the orders of each $x_{i}$). Because the eigenvalues are algebraic integers, to show they are integral it suffices to show that they are rational, and it suffices to show $\lambda _{\chi }$ is fixed under any automorphism $\sigma$ of $\mathbb {Q} (\zeta )$. There must be some $k$ relatively prime to $m$ such that $\sigma (\chi (x_{i}))=\chi (x_{i}^{k})$ for all $i$, and because $S$ is both Eulerian and normal, $\sigma (\chi (x_{i}))=\chi (x_{j})$ for some $j$. Sending $x\mapsto x^{k}$ bijects conjugacy classes, so $\operatorname {Cl} (x_{i})$ and $\operatorname {Cl} (x_{j})$ have the same size and $\sigma$ merely permutes terms in the sum for $\lambda _{\chi }$. Therefore $\lambda _{\chi }$ is fixed for all automorphisms of $\mathbb {Q} (\zeta )$, so $\lambda _{\chi }$ is rational and thus integral.

Consequently, if $G=A_{n}$ is the alternating group and $S$ is a set of permutations given by $\{(12i)^{\pm 1}\}$, then the Cayley graph $\Gamma (A_{n},S)$ is integral. (This solved a previously open problem from the Kourovka Notebook.) In addition when $G=S_{n}$ is the symmetric group and $S$ is either the set of all transpositions or the set of transpositions involving a particular element, the Cayley graph $\Gamma (G,S)$ is also integral.

History

Cayley graphs were first considered for finite groups by Arthur Cayley in 1878. Max Dehn in his unpublished lectures on group theory from 1909–10 reintroduced Cayley graphs under the name Gruppenbild (group diagram), which led to the geometric group theory of today. His most important application was the solution of the word problem for the fundamental group of surfaces with genus ≥ 2, which is equivalent to the topological problem of deciding which closed curves on the surface contract to a point.

Bethe lattice

Main article: Bethe lattice

The Bethe lattice or infinite Cayley tree is the Cayley graph of the free group on $n$ generators. A presentation of a group $G$ by $n$ generators corresponds to a surjective map from the free group on $n$ generators to the group $G,$ and at the level of Cayley graphs to a map from the infinite Cayley tree to the Cayley graph. This can also be interpreted (in algebraic topology) as the universal cover of the Cayley graph, which is not in general simply connected.

See also

• Vertex-transitive graph
• Generating set of a group
• Lovász conjecture
• Cube-connected cycles
• Algebraic graph theory
• Cycle graph (algebra)

External links

• Cayley diagrams
• Weisstein, Eric W. "Cayley graph". MathWorld.