Euclidean minimum spanning tree: Difference between revisions
→Higher dimensions: for the same number of points |
→References: see conference version |
||
| Line 356: | Line 356: | ||
| title = Minimum spanning trees in <math>d</math> dimensions |
| title = Minimum spanning trees in <math>d</math> dimensions |
||
| volume = 6 |
| volume = 6 |
||
| year = 1999}}. This version of this paper is not available online; instead, see the 1997 conference version of the same paper, {{doi|10.1007/3-540-63397-9_26}}.</ref> |
|||
| year = 1999}}</ref> |
|||
<ref name=lobwei>{{citation |
<ref name=lobwei>{{citation |
||
Revision as of 22:31, 7 June 2022
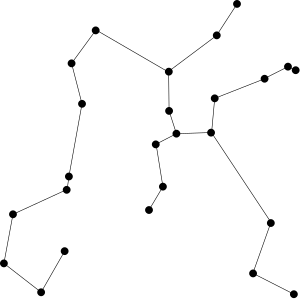
A Euclidean minimum spanning tree is a minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space. It connects the points by a system of line segments, so that any two points can reach each other along a path through the line segments, and it selects line segments that minimize the sum of the Euclidean distances between directly-connected pairs of points.
The edges of the minimum spanning tree meet at angles of at least 60°, at most six to a vertex. In higher dimensions, the number of edges per vertex is controlled by the kissing number of tangent unit spheres. The total length of the edges, for points in a unit square, is at most proportional to the square root of the number of points. Each edge lies in an empty region of the plane, and these regions can be used to prove that the Euclidean minimum spanning tree a subgraph of other geometric graphs including the relative neighborhood graph and Delaunay triangulation. By constructing the Delaunay triangulation and then applying a graph minimum spanning tree algorithm, a Euclidean minimum spanning tree for given planar points may be found in time , as expressed in Big O notation. Faster randomized algorithms are known for points with integer coordinates. For points in higher dimensions, finding an optimal algorithm remains an open problem.
A Euclidean minimum spanning tree, for a set of points in the Euclidean plane or Euclidean space, is a system of line segments, having only the given points as their endpoints, whose union includes all of the points in a connected set, and which has the minimum possible total length of any such system. It is never helpful to form a closed cycle of line segments (a polygon), because one edge of any cycle could be removed, reducing the length while preserving connectivity. Therefore, any minimum-length connecting set of line segments is a tree, and one can equivalently define a Euclidean minimum spanning tree as a tree of line segments between pairs of the given points, with minimum total length.[1] The given points, and line segments connecting pairs of points, may be represented abstractly as the vertices and edges of a complete graph, with the weight of each edge given by the length of its line segment, and a Euclidean minimum spanning tree is a minimum spanning tree of this weighted graph.[2] A given set of points may have more than one Euclidean minimum spanning tree. For instance, for the vertices of a regular polygon, removing any edge of the polygon produces a minimum spanning tree.[3]
A closely related problem is the Steiner tree problem, which again seeks a system of line segments connecting all given points, but without requiring the segments to start and end only at given points. In the Steiner tree problem, additional points may be added as segment endpoints, allowing the Steiner tree to be shorter than the Euclidean minimum spanning tree.[4] In another related problem, the Euclidean traveling salesperson path problem, the connecting line segments must again start and end at the given points, but with the additional restriction that each point touches at most two of the line segments. Because of this additional restriction, the optimal traveling salesperson path may be longer than the Euclidean minimum spanning tree, but it is at most twice as long.[2] The paths connecting pairs of points in a Euclidean spanning tree may be much longer than the Euclidean distance between the points; geometric spanners connect all pairs of points by short paths, but generally have cycles rather than being trees.[5]
Properties
Angles and vertex degrees
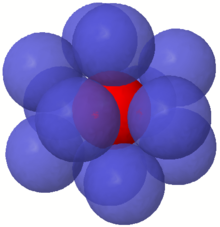
When any two edges of a Euclidean minimum spanning tree meet at a vertex, they must form an angle of 60° or more, with equality only when they form two sides of an equilateral triangle. This is because, for two edges forming any sharper angle, one of the two edges could be replaced by the shorter third edge of the triangle they form, leading to a tree with smaller total length.[6] This angle bound contrasts with the angles at vertices in the Steiner tree problem: an optimal Steiner tree has all angles at least 120°.[4]
When a vertex in a tree has all angles at least 60°, one can form a system of non-overlapping unit spheres centered at that vertex and at the points two units away from it along each edge; each of these spheres is tangent to the central sphere. Conversely, when a system of non-overlapping unit spheres are all tangent to a central sphere, the center points of the spheres have a Euclidean minimum spanning tree with edges from each outer center point to the central point. Therefore, the maximum possible degree of a vertex in a Euclidean minimum spanning tree (the number of edges touching that vertex) equals the kissing number, the maximum number of unit spheres that can touch a central unit sphere without crossing it. In particular this means that planar Euclidean minimum spanning trees have maximum degree at most six (or, for points in general position, five) and three-dimensional Euclidean minimum spanning trees have maximum degree at most twelve.[7] Although it is possible for a planar Euclidean minimum spanning tree to have vertices of degree six, every set of points has some minimum spanning tree with maximum degree five.[8]
For points generated at random from a given continuous distribution, the Euclidean minimum spanning tree is almost surely unique. The numbers of vertices of any given degree (if that degree is possible) converge, for large number of vertices, to a constant times that number of vertices. The values of these constants depend on the degree and the distribution. However, even for simple cases such as the number of leaves for points uniformly distributed in a unit square, their precise values are not known.[9]
Empty regions
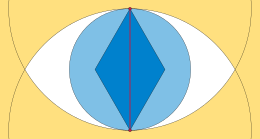
For any edge of any Euclidean minimum spanning tree, the lens (or vesica piscis) formed by intersecting the two circles with as radius cannot have any other given point in its interior. This is because, by the geometry of the two circles, would be closer to both and than they are to each other. If edge were removed from the tree, would remain connected to one of and , but not the other. Replacing the removed edge by or (whichever of these two edges reconnects to the vertex from which it was disconnected) would produce a shorter tree, contradicting the minimality of the initial tree. This contradiction shows that cannot exist. It follows that any other region of the plane within this empty lens must also be empty.[4]
For any edge of any Euclidean minimum spanning tree, the rhombus with angles of 60° and 120°, having as its long diagonal, is disjoint from the rhombi formed in the same way for all other edges. Two edges that share an endpoint cannot have overlapping rhombi, because that could only happen for edges forming an angle sharper than 60°, and two disjoint edges cannot have overlapping rhombi, because if they did then the longer of the two edges could be replaced by a shorter edge among the same four vertices.[4]
Supergraphs
Certain geometric graphs defined from a system of points using empty regions must contain all edges of all Euclidean minimum spanning trees. These include the following:
- The relative neighborhood graph, which has an edge between any pair of points whenever the lens they define is empty.
- The Gabriel graph, which has an edge between any pair of points whenever the circle having the pair as a diameter is empty.
- The Delaunay triangulation, which has an edge between any pair of points whenever there exists an empty circle having the pair as a chord.
- The Urquhart graph, formed from the Delaunay triangulation by removing the longest edge of each triangle. For each remaining edge, the vertices of the Delaunay triangles that use that edge cannot lie within the empty lune of the relative neighborhood graph.
Because the empty-region criteria for these graphs are progressively weaker, these graphs form an ordered sequence of subgraphs. That is, using "⊆" to denote the subset relationship among their edges, these graphs have the relations:
Another graph guaranteed to contain the Euclidean minimum spanning tree is the Yao graph, determined for points in the plane by dividing the plane around each point into six 60° wedges and connecting each point to the nearest neighbor in each wedge. The resulting graph contains the relative neighborhood graph, because two vertices with an empty lens must be the nearest neighbors to each other in their wedges. As with many of the other geometric graphs above, this can be generalized to higher dimensions, and (unlike the Delaunay triangulation) its generalizations always include a linear number of edges.[12][13]
Total length
For points in the unit square (or any other shape of constant diameter), the total length of the Euclidean minimum spanning tree edges is . Some sets of points, such as points evenly spaced in a grid, attain this bound.[4] For points in a unit hypercube in a -dimensional space, the corresponding bound is .[14] The same bound applies to the expected total length of the Euclidean minimum spanning tree for points chosen uniformly and independently from a unit square or unit hypercube.[15] Returning to the unit square, the sum of squared edge lengths of the Euclidean minimum spanning tree is . This bound follows from the property that the edges have disjoint rhombi, with area proportional to the squared edge lengths. The bound on total length in turn follows by combining the Cauchy–Schwarz inequality with the bound on squared edge lengths.[4]
Another way of interpreting these results is that the average edge length for points in a unit square is , proportional to the spacing of points in a regular grid, and that for random points in a unit square the average length is proportional to . However, in the random case, with high probability the longest edge is longer, proportional to . That is, with high probability, some edges of length proportional to are required in a graph that connects all pairs of random points in a unit square. With only shorter edges, these points will remain separated into two or more clusters, formed by removing the longest edge from the spanning tree. The constant of proportionality for this longest edge length, and its distribution around its expected value, are also known.[16]
Any geometric spanner, a subgraph of a complete geometric graph whose shortest paths approximate the Euclidean distance, must have total edge length at least as large as the Euclidean minimum spanning tree, and one of the standard quality measures for geometric spanners is the ratio between the total edge length of a spanner and of the Euclidean minimum spanning tree for the same points. Several methods for constructing spanners such as the greedy geometric spanner achieve a constant bound for this ratio.[5] It has been conjectured that the Steiner ratio, the largest possible ratio between the total length of a Euclidean minimum spanning tree and Steiner tree for the same set of points in the plane, is , the ratio for three points in an equilateral triangle.[4]
Subdivision
If every edge of a Euclidean minimum spanning tree is subdivided, by adding a new point at its midpoint, then the resulting tree is still a minimum spanning tree of the augmented point set. Repeating this subdivision process allows the edges of any Euclidean minimum spanning tree to be subdivided arbitrarily finely. However, subdividing some but not all edges, or subdividing the edges at points other than the midpoint, may produce a point set for which the subdivided tree is not the minimum spanning tree.[17]
Computational complexity
For points in any dimension, the Euclidean minimum spanning tree can be constructed in time by constructing a complete graph with an edge between every pair of points, weighted by Euclidean distance, and then applying a graph minimum spanning tree algorithm such as the Prim–Dijkstra–Jarník algorithm or Borůvka's algorithm on it. These algorithms can be made to take time on complete graphs, unlike another common choice, Kruskal's algorithm, which is slower because it involves sorting all distances.[5] For points in low-dimensional spaces, it is possible to solve the problem more quickly, as detailed below.
Computing Euclidean distances involves a square root calculation. In any comparison of edge weights, this calculation can be avoided by comparing the squares of the Euclidean distances instead instead of the distances themselves. Because this change does not affect the outcome of these comparisons, it does not change the result of the minimum spanning tree computation. As well as speeding up the calculation by avoiding a step, this allows the construction of a minimum spanning tree for points with integer coordinates to be performed exactly using only integer arithmetic.[12]
Two dimensions
A faster approach to finding the Euclidean minimum spanning tree in a plane uses the property that it is a subgraph of the Delaunay triangulation:
- Compute the Delaunay triangulation, which can be done in time. Because the Delaunay triangulation is a planar graph, it has at most edges.
- Label each edge with its (squared) length.
- Run a graph minimum spanning tree algorithm on this graph to find a minimum spanning tree. Since there are edges, this requires time using any of the standard minimum spanning tree algorithms.
The final result is an algorithm taking time.[2]
If the input coordinates are integers and can be used as array indices, faster algorithms are possible: the Delaunay triangulation can be constructed by a randomized algorithm in expected time.[18] Additionally, since the Delaunay triangulation is a planar graph, its minimum spanning tree can be found in linear time by a variant of Borůvka's algorithm that removes all but the cheapest edge between each pair of components after each stage of the algorithm.[5][19] Therefore, the total expected time for this algorithm is .[18]
Higher dimensions
The problem can also be generalized to points in the -dimensional space . In higher dimensions, the connectivity determined by the Delaunay triangulation (which, likewise, partitions the convex hull into -dimensional simplices) contains the minimum spanning tree; however, the triangulation might contain the complete graph.[20] Therefore, finding the Euclidean minimum spanning tree as a spanning tree of the complete graph or as a spanning tree of the Delaunay triangulation both take time. For three dimensions it is possible to find the minimum spanning tree in time , and in any dimension greater than three it is possible to solve it in time
The optimal time complexity for higher dimensional Euclidean minimum spanning trees remains unknown,[21] but it is closely related to the time for computing bichromatic closest pairs. In the bichromatic closest pair problem, the input is a set of points, given two different colors (say, red and blue). The output is a pair of a red point and a blue point with the minimum possible distance. This pair always forms one of the edges in the minimum spanning tree. Therefore, the bichromatic closest pair problem can be solved in the amount of time that it takes to construct a Euclidean minimum spanning tree and scan its edges for the shortest red–blue edge. Conversely, for any red–blue coloring of any subset of a given set of points, the bichromatic closest pair produces one edge of the Euclidean minimum spanning tree. By carefully choosing a sequence of colorings of subsets, and finding the bichromatic closest pair of each subproblem, it is possible to find the Euclidean minimum spanning tree in time proportional to the optimal time for finding bichromatic closest pairs for the same number of points, whatever that optimal time turns out to be.[20][22]
For uniformly random point sets in any bounded dimension, the Yao graph[12] or Delaunay triangulation have linear expected numbers of edges, are guaranteed to contain the minimum spanning tree, and can be constructed in linear expected time.[13][23][24] This allows the minimum spanning tree itself to be constructed in linear time, by using a randomized linear time algorithm for graph minimum spanning trees.[25] However, the poor performance of these methods on inputs coming from clustered data has led algorithm engineering researchers to develop methods with a somewhat slower time bound, for random inputs or inputs whose distances and clustering resemble those of random data, while exhibiting better performance on real-world data.[26][27][28]
A well-separated pair decomposition is a family of pairs of subsets of the given points, so that every pair of points belong to one of these pairs of subsets, and so that all pairs of points coming from the same pair of subsets have approximately the same length. It is possible to find a well-separated pair decomposition with a linear number of subsets, and a representative pair of points for each subset, in time . The minimum spanning tree of the graph formed by these representative pairs is then an approximation to the Euclidean minimum spanning tree. Using these ideas, it is possible to produce a -approximation in time, whenever is a constant. More precisely, by choosing each representative pair to be an approximation to the closest pair in its equivalence class, and varying the quality of this approximation carefully for different pairs, the dependence on in the time bound can be given as for any fixed dimension.[29]
Lower bound
An asymptotic lower bound of of the Euclidean minimum spanning tree problem can be established in restricted models of computation, such as the algebraic decision tree and algebraic computation tree models, in which the algorithm has access to the input points only through certain restricted primitives that perform simple algebraic computations on their coordinates: in these models, the closest pair of points problem requires time, but the closest pair is necessarily an edge of the Euclidean minimum spanning tree, so the Euclidean minimum spanning tree also requires this much time.[30] However, these lower bounds do not apply to models of computation with integer point coordinates, in which bitwise operations and table indexing operations are permitted using those coordinates. In these models, faster algorithms are possible, as described above.[18]
Applications
An obvious application of Euclidean minimum spanning trees is to find the cheapest network of wires or pipes to connect a set of places, assuming the links cost a fixed amount per unit length. The first publications on minimum spanning trees more generally concerned a geographic version of the problem, involving the design of an electrical grid for southern Moravia,[31] and an application to minimizing wire lengths in circuits was described in 1957 by Loberman and Weinberger.[32]
Minimum spanning trees are closely related to single-linkage clustering, one of several methods for hierarchical clustering. This correspondence applies to the Euclidean minimum spanning tree, for clustering points in a Euclidean space. The edges of a Euclidean minimum spanning tree, sorted by their length, give the order in which to merge clusters into larger clusters in this clustering method.[1] Although the long thin cluster shapes produced by single-linkage clustering can be a bad fit for certain types of data, such as mixtures of Gaussian distributions, it can be a good choice in applications where the clusters themselves are expected to have long thin shapes, such as in modeling the dark matter halos of galaxies.[28]
Minimum spanning trees have also been used to infer the shape of curves in the plane, given points sampled along the curve. For a smooth curve, sampled more finely than its local feature size, the minimum spanning tree will form a path connecting consecutive points along the curve. Similar methods can be used more generally to recognize curves drawn in a dotted or dashed style rather than as a single connected set. Applications of this curve-finding technique include particle physics, in automatically identifying the tracks left by particles in a bubble chamber.[33]
Another application of Euclidean minimum spanning trees is a constant-factor approximation algorithm for approximately solving the Euclidean traveling salesman problem, the version of the traveling salesman problem on a set of points in the plane with edges labelled by their length. Walking around the boundary of the minimum spanning tree can approximate the optimal traveling salesman tour within a factor of two of the optimal length.[2] However, more accurate polynomial time approximation schemes are known for this problem.[34]
Realization
The realization problem for Euclidean minimum spanning trees takes an abstract tree as input, and seeks a geometric location for each vertex of the tree (in a space of some fixed dimension) so that the given tree equals the Euclidean minimum spanning tree of points with these locations. Not every abstract tree has such a realization; for instance, the tree must obey the kissing number bound on the degree of each vertex. Additional restrictions beyond this degree restriction exist; for instance, it is not possible for a planar Euclidean minimum spanning tree to have a degree six vertex that is adjacent to a vertex of degree five or six.[8] Determining whether a two-dimensional realization exists is NP-hard. However, the proof that this problem is hard depends on the fact that degree-six vertices in a tree have a very restricted set of realizations: the neighbors of such a vertex must be placed on the vertices of a regular hexagon centered at that vertex.[35] For trees of maximum degree five, a planar realization always exists.[8] Similarly, for trees of maximum degree ten, a three-dimensional realization always exists.[36] For these realizations, some trees may require a bounding box of exponential size, relative to the length of their shortest edge.[37] Trees of maximum degree four have smaller planar realizations, with a bounding box of polynomial area.[38]
See also
- Rectilinear minimum spanning tree, a minimum spanning tree with distances measured using taxicab geometry
References
- ^ a b Gower, J. C.; Ross, G. J. S. (1969), "Minimum spanning trees and single linkage cluster analysis", Applied Statistics, 18: 54–61, doi:10.2307/2346439, JSTOR 2346439, MR 0242315
- ^ a b c d Shamos, Michael Ian; Hoey, Dan (1975), "Closest-point problems", 16th Annual Symposium on Foundations of Computer Science, Berkeley, California, USA, October 13-15, 1975, IEEE Computer Society, pp. 151–162, doi:10.1109/SFCS.1975.8, MR 0426498
- ^ Bose, Prosenjit; Devroye, Luc; Evans, William; Kirkpatrick, David (2006), "On the spanning ratio of Gabriel graphs and β-skeletons", SIAM Journal on Discrete Mathematics, 20 (2): 412–427, doi:10.1137/S0895480197318088, MR 2257270
- ^ a b c d e f g Gilbert, E. N.; Pollak, H. O. (1968), "Steiner minimal trees", SIAM Journal on Applied Mathematics, 16: 1–29, doi:10.1137/0116001, JSTOR 2099400, MR 0223269
- ^ a b c d Eppstein, David (1999), "Spanning trees and spanners" (PDF), in Sack, J.-R.; Urrutia, J. (eds.), Handbook of Computational Geometry, Elsevier, pp. 425–461, MR 1746681
- ^ Georgakopoulos, George; Papadimitriou, Christos H. (1987), "The 1-Steiner tree problem", Journal of Algorithms, 8 (1): 122–130, doi:10.1016/0196-6774(87)90032-0, MR 0875330
- ^ Robins, G.; Salowe, J. S. (1995), "Low-degree minimum spanning trees", Discrete & Computational Geometry, 14 (2): 151–165, doi:10.1007/BF02570700, MR 1331924
- ^ a b c Monma, Clyde; Suri, Subhash (1992), "Transitions in geometric minimum spanning trees", Discrete & Computational Geometry, 8 (3): 265–293, doi:10.1007/BF02293049, MR 1174358
- ^ Steele, J. Michael; Shepp, Lawrence A.; Eddy, William F. (1987), "On the number of leaves of a Euclidean minimal spanning tree", Journal of Applied Probability, 24 (4): 809–826, doi:10.2307/3214207, MR 0913823
- ^ Preparata, Franco P.; Shamos, Michael Ian (1985), Computational Geometry: An Introduction, Texts and Monographs in Computer Science, Springer-Verlag, New York, p. 263, doi:10.1007/978-1-4612-1098-6, ISBN 0-387-96131-3, MR 0805539
- ^ Toussaint, G. T. (1980), "Comment: Algorithms for computing relative neighborhood graph", Electronics Letters, 16 (22): 860, doi:10.1049/el:19800611; reply by Urquhart, pp. 860–861
- ^ a b c Yao, Andrew Chi Chih (1982), "On constructing minimum spanning trees in k-dimensional spaces and related problems", SIAM Journal on Computing, 11 (4): 721–736, doi:10.1137/0211059, MR 0677663
- ^ a b Bentley, Jon Louis; Weide, Bruce W.; Yao, Andrew C. (1980), "Optimal expected-time algorithms for closest point problems", ACM Transactions on Mathematical Software, 6 (4): 563–580, doi:10.1145/355921.355927, MR 0599977
- ^ Steele, J. Michael; Snyder, Timothy Law (1989), "Worst-case growth rates of some classical problems of combinatorial optimization", SIAM Journal on Computing, 18 (2): 278–287, doi:10.1137/0218019, MR 0986667
- ^ Steele, J. Michael (1988), "Growth rates of Euclidean minimal spanning trees with power weighted edges", Annals of Probability, 16 (4): 1767–1787, doi:10.1214/aop/1176991596, JSTOR 2243991, MR 0958215
- ^ Penrose, Mathew D. (1997), "The longest edge of the random minimal spanning tree", The Annals of Applied Probability, 7 (2): 340–361, doi:10.1214/aoap/1034625335, MR 1442317
- ^ Boyce, W. M.; Garey, M. R.; Johnson, D. S. (1978), "A note on bisecting minimum spanning trees", Networks, 8 (3): 187–192, doi:10.1002/net.3230080302, MR 0491324
- ^ a b c Buchin, Kevin; Mulzer, Wolfgang (2011), "Delaunay triangulations in O(sort(n)) time and more", Journal of the ACM, 58 (2): A6:1–A6:27, doi:10.1145/1944345.1944347, MR 2786587
- ^ Mareš, Martin (2004), "Two linear time algorithms for MST on minor closed graph classes" (PDF), Archivum Mathematicum, 40 (3): 315–320, MR 2107027
- ^ a b c Agarwal, P. K.; Edelsbrunner, H.; Schwarzkopf, O.; Welzl, E. (1991), "Euclidean minimum spanning trees and bichromatic closest pairs", Discrete & Computational Geometry, 6 (1), Springer: 407–422, doi:10.1007/BF02574698, MR 1115099
- ^ O'Rourke, J.; Demaine, E. (2001–2002), "Problem 5: Euclidean Minimum Spanning Tree", The Open Problems Project, Smith College
- ^ Krznaric, Drago; Levcopoulos, Christos; Nilsson, Bengt J. (1999), "Minimum spanning trees in dimensions", Nordic Journal of Computing, 6 (4): 446–461, MR 1736451. This version of this paper is not available online; instead, see the 1997 conference version of the same paper, doi:10.1007/3-540-63397-9_26.
- ^ Clarkson, Kenneth L. (1989), "An algorithm for geometric minimum spanning trees requiring nearly linear expected time", Algorithmica, 4 (4): 461–469, doi:10.1007/BF01553902, MR 1019387
- ^ Dwyer, Rex A. (1991), "Higher-dimensional Voronoi diagrams in linear expected time", Discrete & Computational Geometry, 6 (4): 343–367, doi:10.1007/BF02574694, MR 1098813
- ^ Karger, David R.; Klein, Philip N.; Tarjan, Robert E. (1995), "A randomized linear-time algorithm to find minimum spanning trees", Journal of the ACM, 42 (2): 321–328, doi:10.1145/201019.201022, MR 1409738
- ^ Narasimhan, Giri; Zachariasen, Martin; Zhu, Jianlin (2000), "Experiments with computing geometric minimum spanning trees", Proceedings of the 2nd Workshop on Algorithm Engineering and Experiments, pp. 183–196
- ^ Chatterjee, S.; Connor, M.; Kumar, P. (2010), "Geometric minimum spanning trees with GeoFilterKruskal", in Festa, Paola (ed.), Experimental Algorithms: 9th International Symposium, SEA 2010, Ischia Island, Naples, Italy, May 20-22, 2010, Proceedings, Lecture Notes in Computer Science, vol. 6049, Springer-Verlag, pp. 486–500, doi:10.1007/978-3-642-13193-6_41
- ^ a b March, William B.; Ram, Parikshit; Gray, Alexander G. (2010), "Fast Euclidean minimum spanning tree: algorithm, analysis, and applications", in Rao, Bharat; Krishnapuram, Balaji; Tomkins, Andrew; Yang, Qiang (eds.), Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, July 25-28, 2010, pp. 603–612, doi:10.1145/1835804.1835882
- ^ Arya, Sunil; Mount, David M. (2016), "A fast and simple algorithm for computing approximate Euclidean minimum spanning trees", in Krauthgamer, Robert (ed.), Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2016, Arlington, VA, USA, January 10-12, 2016, pp. 1220–1233, doi:10.1137/1.9781611974331.ch85, MR 3478461
- ^ Yao, Andrew Chi-Chih (1991), "Lower bounds for algebraic computation trees with integer inputs", SIAM Journal on Computing, 20 (4): 655–668, doi:10.1137/0220041, MR 1105929
- ^ Graham, R. L.; Hell, Pavol (1985), "On the history of the minimum spanning tree problem", IEEE Annals of the History of Computing, 7 (1): 43–57, doi:10.1109/mahc.1985.10011, MR 0783327
- ^ Loberman, H.; Weinberger, A. (October 1957), "Formal procedures for connecting terminals with a minimum total wire length", Journal of the ACM, 4 (4): 428–437, doi:10.1145/320893.320896
- ^ Zahn, C. T. (1973), "Using the minimum spanning tree to recognize dotted and dashed curves", 1st International Computing Symposium, Davos, Switzerland, 4–7 September 1973
- ^ Bartal, Yair; Gottlieb, Lee-Ad (2013), "A linear time approximation scheme for Euclidean TSP", 54th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2013, 26-29 October, 2013, Berkeley, CA, USA, pp. 698–706, doi:10.1109/FOCS.2013.80, MR 3246273
- ^ Eades, Peter; Whitesides, Sue (1996), "The realization problem for Euclidean minimum spanning trees is NP-hard", Algorithmica, 16 (1): 60–82, doi:10.1007/s004539900037, MR 1394494
- ^ King, James A. (2006), "Realization of degree 10 minimum spanning trees in 3-space" (PDF), Proceedings of the 18th Annual Canadian Conference on Computational Geometry, CCCG 2006, August 14-16, 2006, Queen's University, Ontario, Canada, pp. 39–42
- ^ Angelini, Patrizio; Bruckdorfer, Till; Chiesa, Marco; Frati, Fabrizio; Kaufmann, Michael; Squarcella, Claudio (2014), "On the area requirements of Euclidean minimum spanning trees", Computational Geometry: Theory and Applications, 47 (2, part B): 200–213, doi:10.1016/j.comgeo.2012.10.011, MR 3123788
- ^ Frati, Fabrizio; Kaufmann, Michael (2011), "Polynomial area bounds for MST embeddings of trees", Computational Geometry: Theory and Applications, 44 (9): 529–543, doi:10.1016/j.comgeo.2011.05.005, MR 2819643






























