Electron diffraction: Difference between revisions
→Low Energy Electron Diffraction(LEED): Some refs, also in RHEED |
→Formation of a diffraction pattern: More cites and removal of "diffractogram" |
||
| Line 45: | Line 45: | ||
[[File:ElmagLensScheme.png|left|thumb|300px|Imaging scheme of magnetic lens (center) with magnified image (left) and diffraction pattern (right) formed in back focal plane]] |
[[File:ElmagLensScheme.png|left|thumb|300px|Imaging scheme of magnetic lens (center) with magnified image (left) and diffraction pattern (right) formed in back focal plane]] |
||
In TEM, electron beam passes through a thin film of the examined material. Before and after its interaction with the sample, the beam is |
In TEM, the electron beam passes through a thin film of the examined material. Before and after its interaction with the sample, the beam is manipulated by various elements of electron optics including [[magnetic lens]]es, deflectors or [[apertures]]; these act on the electrons very much like how glass lenses focus lift. Optical elements above the sample are used to control the incident beam which can range from a wide and parallel beam, a focused nanoscopic probe or one which can be smaller than an atom, 0.1nm. As it interacts with the sample, part of the beam is diffracted and part is transmitted through the sample without changing its direction. Which part -- one can never say as electrons are everywhere until they are detected according to the [[Copenhagen interpretation]] |
||
Below the sample, the beam is |
Below the sample, the beam is controlled by a series of [[magnetic lens]]. Each set of initially parallel rays intersect at certain point in the [[back focal plane]] of the first one, called the [[Objective lens]] forming a [[diffraction pattern]]. The diffracted rays intersect at certain distance from the optical axis (related to interplanar distance of the planes diffracting the beam). With a parallel incident beam and a crystalline material, those intersections can be seen as bright diffraction spots . In the image plane below the back focal plane, a magnified image of the sample is formed. Further electron optics allows to select which plane of the optics is projected to the [[Detectors for transmission electron microscopy|microscope camera]] and, therefore, whether a magnified image or diffraction pattern is acquired. Modern microscopes allows one to switch between the imaging and diffraction mode by pressing a single button, which makes diffraction data easily available and accessible;<ref name="Fultz 2013"/> on this page the focus is on what one has when one is collecting a magnified diffraction pattern. |
||
=== Wide parallel beam === |
=== Wide parallel beam === |
||
| Line 59: | Line 59: | ||
[[File:Crystal orientation and diffraction.gif|thumb|300px|left|Diffraction pattern of [[magnesium]] simulated using CrysTBox for various crystal orientations.]] |
[[File:Crystal orientation and diffraction.gif|thumb|300px|left|Diffraction pattern of [[magnesium]] simulated using CrysTBox for various crystal orientations.]] |
||
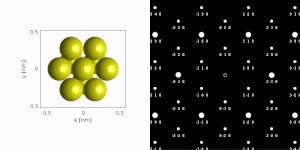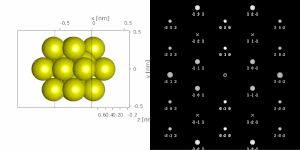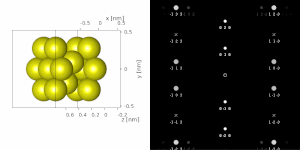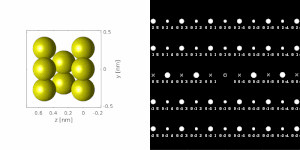
If the sample is tilted relative to the electron beam, diffraction conditions are satisfied for different set of crystallographic planes yielding different types of diffraction spots. This can be used to determine the crystal orientation, which can be used for instance to set the orientation needed for particular experiment, to determine [[misorientation]] between adjacent grains or [[Crystal twinning|crystal twins]].<ref name="De Graef 2003"/><ref name="Klinger 2017"/> Since different sample orientations result in different projections of the reciprocal lattice, they provide an opportunity to reconstruct the three-dimensional information about the crystal structure lost in individual projections. A series of |
If the sample is tilted relative to the electron beam, diffraction conditions are satisfied for different set of crystallographic planes yielding different types of diffraction spots. This can be used to determine the crystal orientation, which can be used for instance to set the orientation needed for particular experiment, to determine [[misorientation]] between adjacent grains or [[Crystal twinning|crystal twins]].<ref name="De Graef 2003"/><ref name="Klinger 2017"/> Since different sample orientations result in different projections of the reciprocal lattice, they provide an opportunity to reconstruct the three-dimensional information about the crystal structure lost in individual projections. A series of diffraction patterns varying in tilt can be acquired and processed using a [[diffraction tomography]] analysis in order to reconstruct an unknown crystal structure. |
||
Apart from limiting the beam using the selected area aperture, localisation can be achieved by condensing the incident beam into a narrow electron probe. This technique is called microprobe or nanoprobe diffraction or simply nanodiffraction. Probes of diameter smaller than 1 nm can be obtained.<ref name="Fultz 2013"/> At these extremes the probe dimension comes at the price of the beam becoming nearly parallel, even though microprobe can be achieved with parallel beam.<ref name="De Graef 2003"/> Compared to SAED, the resulting diffraction spots can be significantly broader, making a manual analysis quite inaccurate. Accurate processing is possible with software like CrysTBox<ref name="Klinger 2017" /> as well as many others<ref>{{cite web |url=https://www.iucr.org/resources/commissions/electron-crystallography/software |title=Freely available software for electron crystallography and electron microscopy |date= 2007|website=www.iucr.org/resources/commissions/electron-crystallography/software |publisher=IUCr |access-date=8 February 2023 }}</ref>, significantly improving accuracy and repeatability of the analysis. |
Apart from limiting the beam using the selected area aperture, localisation can be achieved by condensing the incident beam into a narrow electron probe. This technique is called microprobe or nanoprobe diffraction or simply nanodiffraction. Probes of diameter smaller than 1 nm can be obtained.<ref name="Fultz 2013"/> At these extremes the probe dimension comes at the price of the beam becoming nearly parallel, even though microprobe can be achieved with parallel beam.<ref name="De Graef 2003"/> Compared to SAED, the resulting diffraction spots can be significantly broader, making a manual analysis quite inaccurate. Accurate processing is possible with software like CrysTBox<ref name="Klinger 2017" /> as well as many others<ref>{{cite web |url=https://www.iucr.org/resources/commissions/electron-crystallography/software |title=Freely available software for electron crystallography and electron microscopy |date= 2007|website=www.iucr.org/resources/commissions/electron-crystallography/software |publisher=IUCr |access-date=8 February 2023 }}</ref>, significantly improving accuracy and repeatability of the analysis. |
||
| Line 66: | Line 66: | ||
[[File:SpotToRingDiffraction.gif|right|thumb|Relation between spot and ring diffraction illustrated on 1 to 1000 grains of [[MgO]] using simulation engine of [[CrysTBox]]. Corresponding experimental image can be seen [[#Wide parallel beam|below]].]] |
[[File:SpotToRingDiffraction.gif|right|thumb|Relation between spot and ring diffraction illustrated on 1 to 1000 grains of [[MgO]] using simulation engine of [[CrysTBox]]. Corresponding experimental image can be seen [[#Wide parallel beam|below]].]] |
||
The character of the resulting diffraction pattern depends on whether the beam is diffracted by one [[single crystal]] or by number of differently oriented crystallites for instance in a polycrystalline material. A single-crystalline |
The character of the resulting diffraction pattern depends on whether the beam is diffracted by one [[single crystal]] or by number of differently oriented crystallites for instance in a polycrystalline material. A single-crystalline diffraction pattern shows a regular pattern of bright spots. This pattern can be seen as a two-dimensional projection of the [[reciprocal lattice|reciprocal crystal lattice]]. If there are more contributing crystallites, the diffraction image becomes a superposition of individual crystals' diffraction patterns. Ultimately, this superposition contains diffraction spots of all possible crystallographic plane systems in all possible orientations. This results in a pattern of [[concentric]] rings of discrete radii for the following reasons: |
||
# The discreteness of ring radii is given by the fact, that there are discrete spacings between various parallel crystallographic planes in a given crystal system and therefore the beams satisfying the diffraction condition can only form diffraction spots in discrete distances from the transmitted beam. |
# The discreteness of ring radii is given by the fact, that there are discrete spacings between various parallel crystallographic planes in a given crystal system and therefore the beams satisfying the diffraction condition can only form diffraction spots in discrete distances from the transmitted beam. |
||
# The concentricity and ringlike shape is given by the fact, that there are all possible orientations of crystallographic planes and therefore the diffraction spots are formed all around the transmitted beam (rings centre) at the distance (ring radius) corresponding to a particular crystallographic plane. |
# The concentricity and ringlike shape is given by the fact, that there are all possible orientations of crystallographic planes and therefore the diffraction spots are formed all around the transmitted beam (rings centre) at the distance (ring radius) corresponding to a particular crystallographic plane. |
||
| Line 78: | Line 78: | ||
}} |
}} |
||
If the illuminated area selected by the aperture covers many differently oriented crystallites, their diffraction patterns superimpose forming an image of concentric rings. The ring diffraction pattern is typical for polycrystalline samples, powders or nanoparticles. A diameter of each ring corresponds to interplanar distances in the sample. Instead of information about individual grains or sample orientation, this provides statistical information for instance about overall crystallinity or texture. Textured materials can be recognized by a non-uniform distribution of intensity along the ring circumference despite sufficient crystallinity. Ring |
If the illuminated area selected by the aperture covers many differently oriented crystallites, their diffraction patterns superimpose forming an image of concentric rings. The ring diffraction pattern is typical for polycrystalline samples, powders or nanoparticles. A diameter of each ring corresponds to interplanar distances in the sample. Instead of information about individual grains or sample orientation, this provides statistical information for instance about overall crystallinity or texture. Textured materials can be recognized by a non-uniform distribution of intensity along the ring circumference despite sufficient crystallinity. Ring diffraction patterns can be also used to discriminate between nanocrystalline and amorphous phases.<ref name="De Graef 2003"/> |
||
=== Multiple materials and double diffraction === |
=== Multiple materials and double diffraction === |
||
| Line 102: | Line 102: | ||
=== 4D STEM === |
=== 4D STEM === |
||
{{main|4D scanning transmission electron microscopy}} |
{{main|4D scanning transmission electron microscopy}} |
||
4D scanning transmission electron microscopy (4D STEM) is a subset of [[scanning transmission electron microscopy]] (STEM) which utilizes a pixelated electron detector to capture a [[convergent beam electron diffraction]] (CBED) pattern at each scan location; see that page's history for attribution. This technique captures a 2 dimensional reciprocal space image associated with each scan point as the beam rasters across a 2 dimensional region in real space, hence the name 4D STEM. Its development was enabled by evolution in STEM detectors and improvements computational power. The technique has applications in visual diffraction imaging, phase orientation and strain mapping, phase contrast analysis, among others. |
4D scanning transmission electron microscopy (4D STEM) is a subset of [[scanning transmission electron microscopy]] (STEM) methods which utilizes a pixelated electron detector to capture a [[convergent beam electron diffraction]] (CBED) pattern at each scan location; see that page's history for attribution. This technique captures a 2 dimensional reciprocal space image associated with each scan point as the beam rasters across a 2 dimensional region in real space, hence the name 4D STEM. Its development was enabled by evolution in STEM detectors and improvements in computational power. The technique has applications in visual diffraction imaging, phase orientation and strain mapping, phase contrast analysis, among others; it has become very popular and rapidly involving from about 2020 onwards. |
||
The name 4D STEM is common in literature, however it is known by other names: 4D STEM [[EELS]], ND STEM (N- since the number of dimensions could be higher than 4), position resolved diffraction (PRD), spatial resolved diffractometry, momentum-resolved [[Scanning transmission electron microscopy|STEM]], "nanobeam precision electron diffraction", scanning electron nano diffraction, nanobeam electron diffraction, or pixelated [[Scanning transmission electron microscopy|STEM]].<ref>{{cite web |title=4D STEM {{!}} Gatan, Inc. |url=https://www.gatan.com/techniques/4d-stem |access-date=2022-03-13 |website=www.gatan.com |language=en}}</ref> |
The name 4D STEM is common in literature, however it is known by other names: 4D STEM [[EELS]], ND STEM (N- since the number of dimensions could be higher than 4), position resolved diffraction (PRD), spatial resolved diffractometry, momentum-resolved [[Scanning transmission electron microscopy|STEM]], "nanobeam precision electron diffraction", scanning electron nano diffraction, nanobeam electron diffraction, or pixelated [[Scanning transmission electron microscopy|STEM]].<ref>{{cite web |title=4D STEM {{!}} Gatan, Inc. |url=https://www.gatan.com/techniques/4d-stem |access-date=2022-03-13 |website=www.gatan.com |language=en}}</ref> |
||
| Line 109: | Line 109: | ||
{{main|Low-energy electron diffraction}} |
{{main|Low-energy electron diffraction}} |
||
[[Image:Si100Reconstructed.png|thumbnail|280x280px|'''Figure 1''': LEED pattern of a Si(100) reconstructed surface. The underlying lattice is a square lattice, while the [[surface reconstruction]] has a 2x1 periodicity. Also seen is the electron gun that generates the primary electron beam; it covers up parts of the screen.]] |
[[Image:Si100Reconstructed.png|thumbnail|280x280px|'''Figure 1''': LEED pattern of a Si(100) reconstructed surface. The underlying lattice is a square lattice, while the [[surface reconstruction]] has a 2x1 periodicity. Also seen is the electron gun that generates the primary electron beam; it covers up parts of the screen.]] |
||
Low-energy electron diffraction (LEED) is a technique for the determination of the surface structure of [[single crystal|single-crystalline]] materials by bombardment with a [[collimated beam]] of low-energy electrons (30–200 |
Low-energy electron diffraction (LEED) is a technique for the determination of the surface structure of [[single crystal|single-crystalline]] materials by bombardment with a [[collimated beam]] of low-energy electrons (30–200 eV)<ref name="Oura">{{cite book |author1=K. Oura |author2=V. G. Lifshifts |author3=A. A. Saranin |author4=A. V. Zotov |author5=M. Katayama |title=Surface Science |url=https://archive.org/details/surfacesciencein00oura_931 |url-access=limited |publisher=Springer-Verlag, Berlin Heidelberg New York |date=2003 |pages=[https://archive.org/details/surfacesciencein00oura_931/page/n10 1]–45|isbn=9783540005452 }}</ref> and observation of diffracted electrons as spots on a fluorescent screen; see the orignal page's history for attribution and references<ref>{{Cite journal |last=Viefhaus |first=H. |date=1987 |title=Low-energy electron diffraction. Von M. A. Van Hove, W. H. Weinberg und C.-M. Chn. Springer-Verlag Berlin - Heidelberg - New York -London -Paris -Tokyo 1986. XVII, 603 S., 213 Abb., DM 124,-.ISBN 3-540-16262-3 |url=https://onlinelibrary.wiley.com/doi/10.1002/maco.19870380711 |journal=Materials and Corrosion/Werkstoffe und Korrosion |language=de |volume=38 |issue=7 |pages=404–404 |doi=10.1002/maco.19870380711 |issn=0947-5117}}</ref><ref>{{Cite book |last=Moritz |first=Wolfgang |url=https://www.worldcat.org/oclc/1293917727 |title=Surface structure determination by LEED and X-rays |date=2022 |others=M. A. Van Hove |isbn=978-1-108-28457-8 |location=Cambridge, United Kingdom |oclc=1293917727}}</ref>. It has been used to solve a very large number of relatively simple surface structures of metals and semiconductors, plus cases with simple chemisorbants. For more complex cases transmission electron diffraction<ref>{{Cite journal |last=Takayanagi |first=K. |last2=Tanishiro |first2=Y. |last3=Takahashi |first3=M. |last4=Takahashi |first4=S. |date=1985 |title=Structural analysis of Si(111)‐7×7 by UHV‐transmission electron diffraction and microscopy |url=http://avs.scitation.org/doi/10.1116/1.573160 |journal=Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films |language=en |volume=3 |issue=3 |pages=1502–1506 |doi=10.1116/1.573160 |issn=0734-2101}}</ref><ref>{{Cite journal |last=Gilmore |first=C.J. |last2=Marks |first2=L.D. |last3=Grozea |first3=D. |last4=Collazo |first4=C. |last5=Landree |first5=E. |last6=Twesten |first6=R.D. |date=1997 |title=Direct solutions of the Si(111) 7 × 7 structure |url=https://linkinghub.elsevier.com/retrieve/pii/S0039602897000629 |journal=Surface Science |language=en |volume=381 |issue=2-3 |pages=77–91 |doi=10.1016/S0039-6028(97)00062-9}}</ref> or surface x-ray diffraction<ref>{{Cite journal |last=Robinson |first=I. K. |date=1983-04-11 |title=Direct Determination of the Au(110) Reconstructed Surface by X-Ray Diffraction |url=https://link.aps.org/doi/10.1103/PhysRevLett.50.1145 |journal=Physical Review Letters |language=en |volume=50 |issue=15 |pages=1145–1148 |doi=10.1103/PhysRevLett.50.1145 |issn=0031-9007}}</ref> have been used, often with [[scanning tunnelling microscopy]] and [[density functional theory]] calculations. |
||
LEED may be used in one of two ways: |
|||
# Qualitatively, where the diffraction pattern is recorded and analysis of the spot positions gives information on the symmetry of the surface structure. In the presence of an [[adsorbate]] the qualitative analysis may reveal information about the size and rotational alignment of the adsorbate unit cell with respect to the substrate unit cell. |
|||
# Quantitatively, where the intensities of diffracted beams are recorded as a function of incident electron beam energy to generate the so-called I–V curves. By comparison with theoretical curves, these may provide accurate information on atomic positions on the surface at hand. |
|||
=== Reflection High Energy Electron Diffraction (RHEED) === |
=== Reflection High Energy Electron Diffraction (RHEED) === |
||
{{main|RHEED}} |
{{main|RHEED}} |
||
RHEED, see that page's history for attribution, is a [[analytical technique|technique]] used to characterize the surface of [[crystalline]] materials. RHEED systems gather information only from the surface layers of the sample, which distinguishes RHEED from other [[material characterization|materials characterization]] methods that also rely on diffraction of high-energy [[electrons]]. [[Transmission electron microscopy]], another common electron diffraction method samples mainly the bulk of the sample due to the geometry of the system, although in special cases it can provide surface information<ref>{{Cite journal |last=Kienzle |first=Danielle M. |last2=Marks |first2=Laurence D. |date=2012 |title=Surface transmission electron diffraction for SrTiO3 surfaces |url=http://xlink.rsc.org/?DOI=c2ce25204j |journal=CrystEngComm |language=en |volume=14 |issue=23 |pages=7833 |doi=10.1039/c2ce25204j |issn=1466-8033}}</ref>. [[Low-energy electron diffraction]] (LEED) is also surface sensitive, but LEED achieves surface sensitivity through the use of low energy electrons. The main uses of RHEED to date have been during thin film growth, as the geometry is amenable to simultaneous collection of the diffraction data and deposition. |
RHEED, see that page's history for attribution and also references<ref>{{Cite book |last=Ichimiya |first=Ayahiko |url=https://www.worldcat.org/oclc/54529276 |title=Reflection high-energy electron diffraction |date=2004 |publisher=Cambridge University Press |others=Philip I. Cohen |isbn=0-521-45373-9 |location=Cambridge, U.K. |oclc=54529276}}</ref> , is a [[analytical technique|technique]] used to characterize the surface of [[crystalline]] materials. RHEED systems gather information only from the surface layers of the sample, which distinguishes RHEED from other [[material characterization|materials characterization]] methods that also rely on diffraction of high-energy [[electrons]]. [[Transmission electron microscopy]], another common electron diffraction method samples mainly the bulk of the sample due to the geometry of the system, although in special cases it can provide surface information<ref>{{Cite journal |last=Kienzle |first=Danielle M. |last2=Marks |first2=Laurence D. |date=2012 |title=Surface transmission electron diffraction for SrTiO3 surfaces |url=http://xlink.rsc.org/?DOI=c2ce25204j |journal=CrystEngComm |language=en |volume=14 |issue=23 |pages=7833 |doi=10.1039/c2ce25204j |issn=1466-8033}}</ref>. [[Low-energy electron diffraction]] (LEED) is also surface sensitive, but LEED achieves surface sensitivity through the use of low energy electrons. The main uses of RHEED to date have been during thin film growth<ref>{{Cite book |last=Braun |first=Wolfgang |url=https://www.worldcat.org/oclc/40857022 |title=Applied RHEED : reflection high-energy electron diffraction during crystal growth |date=1999 |publisher=Springer |isbn=3-540-65199-3 |location=Berlin |oclc=40857022}}</ref>, as the geometry is amenable to simultaneous collection of the diffraction data and deposition. |
||
=== Kikuchi lines === |
=== Kikuchi lines === |
||
| Line 120: | Line 125: | ||
[[File:Kikuchi.png|thumb|left|300px|Crystallographic planes in [0 1 1] [[Mg]] cell with corresponding diffraction spots and Kikuchi lines simulated in CrysTBox]] |
[[File:Kikuchi.png|thumb|left|300px|Crystallographic planes in [0 1 1] [[Mg]] cell with corresponding diffraction spots and Kikuchi lines simulated in CrysTBox]] |
||
Kikuchi lines are linear |
Kikuchi lines are linear features created by electrons scattered both inelastically and elastically. As the electron beam interacts with matter, the electrons are diffracted via [[elastic scattering]], and also scattered [[inelastic scattering|inelastically]] losing part of their kinetic energy. These occur simultaneously, and one cannot separate them -- the [[Copenhagen interpretation]]. These electrons form Kikuchi lines which provide information on the orientation.<ref name="Morniroli 2004"/> |
||
Kikuchi lines are come in pairs forming Kikuchi bands. They are indexed in terms of the crystallographic planes they are connected to. The angular width of the band is equal to the diffraction angle <math>\theta_1</math> specified above which means, that in the |
Kikuchi lines are come in pairs forming Kikuchi bands. They are indexed in terms of the crystallographic planes they are connected to. The angular width of the band is equal to the diffraction angle <math>\theta_1</math> specified above which means, that in the diffraction pattern, the width of <math>(hkl)</math> plane will be equal to the distance between transmitted beam and <math>(hkl)</math> diffraction spot. The position of Kikuchi bands is fixed with respect to each other and the orientation of the sample, but not against the diffraction spots or the direction of the incident electron beam. As the crystal is tilted in the electron beam, the bands move on the diffraction pattern.<ref name="Morniroli 2004"/> |
||
Kikuchi lines occur in TEM especially in thicker samples, where simultaneous inelastic and elastic scattering occurs. Since the position of Kikuchi bands |
Kikuchi lines occur in TEM especially in thicker samples, where simultaneous inelastic and elastic scattering occurs. Since the position of Kikuchi bands is quite sensitive to crystal orientation, they can be used to fine-tune a zone-axis orientation. Alternatively, they can be used to determine crystal orientation with significantly higher accuracy than what is feasible with a spot diffraction analysis. Since mutual positions and orientations of Kikuchi bands is fixed with respect to the crystal, and since the bands intersect in low-index zone axes, they can be used for navigation when changing the orientation between zone axes connected by some band. For those purposes, Kikuchi maps are available.<ref name="Fultz 2013"/> |
||
=== Diffraction by individual molecules in gases === |
=== Diffraction by individual molecules in gases === |
||
| Line 149: | Line 154: | ||
:<math> I_m(s) = \frac{K^2}{R^2} I_0 \sum_{i=1}^N \sum_{\stackrel{j=1}{i\neq j}}^N \left| f_i(s) \right| \left| f_j(s)\right| \frac{\sin [s(r_{ij}-\kappa s^2)]}{sr_{ij}}e^{-(1/2 l_{ij} s^2)} \cos [\eta _i (s) -\eta _i (s)] ,</math> |
:<math> I_m(s) = \frac{K^2}{R^2} I_0 \sum_{i=1}^N \sum_{\stackrel{j=1}{i\neq j}}^N \left| f_i(s) \right| \left| f_j(s)\right| \frac{\sin [s(r_{ij}-\kappa s^2)]}{sr_{ij}}e^{-(1/2 l_{ij} s^2)} \cos [\eta _i (s) -\eta _i (s)] ,</math> |
||
where <math>r_{ij}</math> is the distance between two atoms, <math>l_{ij}</math> is the mean square amplitude of vibration between the two atoms, <math>\kappa</math> is the anharmonicity constant and <math>\eta</math>is a phase factor which is important for atomic pairs with very different nuclear charges. The summation is performed over all atom pairs. Atomic triplet intensity <math>I_t(s)</math> is negligible in most cases. If the molecular intensity is extracted from an experimental |
where <math>r_{ij}</math> is the distance between two atoms, <math>l_{ij}</math> is the mean square amplitude of vibration between the two atoms, <math>\kappa</math> is the anharmonicity constant and <math>\eta</math>is a phase factor which is important for atomic pairs with very different nuclear charges. The summation is performed over all atom pairs. Atomic triplet intensity <math>I_t(s)</math> is negligible in most cases. If the molecular intensity is extracted from an experimental pattern by subtracting other contributions, it can be used to match and refine a structural model against the experimental data. |
||
=== In scanning electron microscope === |
=== In scanning electron microscope === |
||
Revision as of 21:32, 8 February 2023

Electron diffraction refers to changes in the direction of electron beams due to atomic structures generating diffraction patterns which are widely used for analysis of materials. Electron diffraction can also refer to a set of experimental techniques used for material characterization. This technique is similar to X-ray and neutron diffraction.
Electron diffraction is most frequently used in chemistry, materials science, geology and solid state physics to study crystalline, quasi-crystalline and amorphous materials using electron microscopes. In these instruments, electrons are accelerated to reasonably high energies both to shorten their wavelength and so that they can penetrate solids. With the wavelength sufficiently short, the atomic structure changes the directions of the electrons generating ordered diffraction patterns, which carry information about the crystal orientation, lattices, crystal defects as well as other information.
In order to be diffracted, electrons need to interact with matter. Due to their negative electric charge, their interactions differ from other radiation used in diffraction studies of materials such as X-rays and neutrons. Negative electrons are scattered due to Coulomb forces when they interact with both the positively charged atomic core and the negatively charged electrons around the atoms. In comparison, X-rays are scattered after interactions with only the electrons, specifically the electron density, while neutrons are scattered by the atomic nuclei through the strong nuclear force.[1]
Electron diffraction occurs as the result of an elastic scattering, when there is no change in the kinetic energy of the electrons during their interactions with atoms. One can also have combined inelastically scattered and elastic scattering of electrons.
In transmission electron microscopy (TEM), the most frequent technique related to electron diffraction is selected area diffraction which is often used to measure the arrangement of atoms by comparing to standards. In most cases this is semiquantitative, but it can be made quantitative. In scanning electron microscopy (SEM), electron backscatter diffraction is used to determine crystal orientation across the sample. The potential of electron diffraction is not limited to solids. It can be used to characterize individual molecules dispersed in a gaseous atmosphere using gas electron diffraction, surfaces using lower energy electrons, called LEED, and by reflecting electrons off surfaces, called RHEED.
History
Experiments involving electron beams occurred long before the discovery of the electron. In 1650, Otto von Guericke invented the vacuum pump[2] allowing physicists to study the effects of high voltage electricity passing through rarefied air. It was observed that an electrostatic generator produced sparks which travel a longer distance through low pressure air than through atmospheric pressure air. In 1857, German physicist Heinrich Geissler was able to achieve a pressure of around 10−3 atm and with voltages between a few kilovolts and 100 kV he observed glow discharge. By the 1870s, British physicist William Crookes and others were able to evacuate tubes below 10−6 atm and observed, that the glow in the whole tube disappeared with lowering pressure but the glass behind the anode began to glow. The reason was, that the low pressure allowed the electrons to travel from cathode to the anode without collisions. Even though they were attracted to the anode, some passed the anode and collided with the tube wall behind making it glow.
The electron beam was discovered in 1869 by German physicist Johann Hittorf.[3] He noticed a shadow cast by the anode on the tube wall behind the anode. He correctly deduced that there must be rays emitted from the cathode. Another German scientist Eugen Goldstein named them cathode rays[4] (German kathodenstrahlen). In 1897, Joseph Thomson measured the mass of cathode rays proving they were made of particles. These particles, however, were 1800 times lighter than the lightest particle known at that time - a hydrogen atom. Therefore, the first subatomic particle was discovered, originally called corpuscle and later named electron. Thomson also showed electrons were identical with particles given off by the photoelectric effect and radioactive materials.[5]
Thomson's discovery did not itself lead to an understanding of electron diffraction. Light diffraction was first described in the 17th century by Italian priest and physicist Francesco Maria Grimaldi.[6] Light was shown to be a wave in 1803 when British scientist Thomas Young performed his experiment with two slits.[7] The wave theory was further supported by studies and calculations of French physicist Augustin-Jean Fresnel 1816[8] and 1818[9] finally confirming theory of Christiaan Huygens.[10]
Understanding of the nature of electron beams was fundamentally changed in 1925, when French physicist Louis de Broglie published his hypothesis.[11] He stated that all matter particles can behave as waves and, among other important implications, can be diffracted. The de Broglie hypothesis was experimentally confirmed for electrons in two experiments performed independently by George Paget Thomson[12] and Clinton Joseph Davisson. This sparked a rapid development of electron-based analytical techniques in the 1930s from gas electron diffraction invented by Herman Mark to the first electron microscopes developed by Ernst Ruska.[13]
Types of electron diffraction
In transmission electron microscope
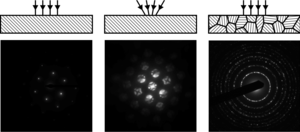
Electron diffraction in a Transmission electron microscopy (TEM) is a versatile technique allowing to determine a wide range of crystallographic quantities. The versatility of TEM originates from its ability to form the electron beam using complex electron optics. Good control of the beam geometry allows to perform various diffraction techniques enabling to measure the crystal lattice constants, study crystal defects or even to reconstruct an unknown crystal structure.
Even though the diffraction analysis in TEM is a strong analytical tool itself, it can be supported by other tools available in TEM either naturally or as an optional equipment. Among other methods, TEM provides magnified sample image or even high-resolution image, chemical analysis through energy-dispersive X-ray spectroscopy, investigations of electronic structure and bonding through electron energy loss spectroscopy, and studies of the mean inner potential through electron holography.
Compared to another widely used material characterization technique, X-ray diffraction, TEM analysis is significantly more localized.
Formation of a diffraction pattern
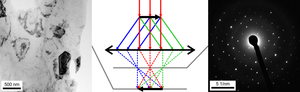
In TEM, the electron beam passes through a thin film of the examined material. Before and after its interaction with the sample, the beam is manipulated by various elements of electron optics including magnetic lenses, deflectors or apertures; these act on the electrons very much like how glass lenses focus lift. Optical elements above the sample are used to control the incident beam which can range from a wide and parallel beam, a focused nanoscopic probe or one which can be smaller than an atom, 0.1nm. As it interacts with the sample, part of the beam is diffracted and part is transmitted through the sample without changing its direction. Which part -- one can never say as electrons are everywhere until they are detected according to the Copenhagen interpretation
Below the sample, the beam is controlled by a series of magnetic lens. Each set of initially parallel rays intersect at certain point in the back focal plane of the first one, called the Objective lens forming a diffraction pattern. The diffracted rays intersect at certain distance from the optical axis (related to interplanar distance of the planes diffracting the beam). With a parallel incident beam and a crystalline material, those intersections can be seen as bright diffraction spots . In the image plane below the back focal plane, a magnified image of the sample is formed. Further electron optics allows to select which plane of the optics is projected to the microscope camera and, therefore, whether a magnified image or diffraction pattern is acquired. Modern microscopes allows one to switch between the imaging and diffraction mode by pressing a single button, which makes diffraction data easily available and accessible;[1] on this page the focus is on what one has when one is collecting a magnified diffraction pattern.
Wide parallel beam

The simplest diffraction technique in TEM is selected area (electron) diffraction (SAED) for which the incident beam is wide and parallel. In order to select a particular region of interest from which the diffraction is collected, a selected area aperture is used. It is located below the sample, and can be positioned so that it only allows to pass the wanted portion of the electron beam, blocking the rest. This way diffraction information can be limited to, for instance, individual crystallites. Unfortunately the method is limited by the spherical aberration of the objective lens, so is only accurate for large grains.
If a parallel beam is used to acquire a diffraction pattern from a single-crystal, the resulting image is similar to a two-dimensional projection of the crystal reciprocal lattice. From this one can determine interplanar distances and angles and in some cases crystal symmetry. In combination with modern automated analytical software such as CrysTBox, SAED can be used for a quantitative analysis with reasonable precision.[14] However, projector lens aberrations as well as dynamical diffraction effects cannot be ignored. For instance, certain diffraction spots which are not present in x-ray diffraction can appear, for instance Gjonnes-Moodie extinction conditions[15]. Hence x-ray diffraction remains the preferred method for precise lattice parameters.
If the sample is tilted relative to the electron beam, diffraction conditions are satisfied for different set of crystallographic planes yielding different types of diffraction spots. This can be used to determine the crystal orientation, which can be used for instance to set the orientation needed for particular experiment, to determine misorientation between adjacent grains or crystal twins.[16][14] Since different sample orientations result in different projections of the reciprocal lattice, they provide an opportunity to reconstruct the three-dimensional information about the crystal structure lost in individual projections. A series of diffraction patterns varying in tilt can be acquired and processed using a diffraction tomography analysis in order to reconstruct an unknown crystal structure.
Apart from limiting the beam using the selected area aperture, localisation can be achieved by condensing the incident beam into a narrow electron probe. This technique is called microprobe or nanoprobe diffraction or simply nanodiffraction. Probes of diameter smaller than 1 nm can be obtained.[1] At these extremes the probe dimension comes at the price of the beam becoming nearly parallel, even though microprobe can be achieved with parallel beam.[16] Compared to SAED, the resulting diffraction spots can be significantly broader, making a manual analysis quite inaccurate. Accurate processing is possible with software like CrysTBox[14] as well as many others[17], significantly improving accuracy and repeatability of the analysis.
Polycrystalline Pattern

The character of the resulting diffraction pattern depends on whether the beam is diffracted by one single crystal or by number of differently oriented crystallites for instance in a polycrystalline material. A single-crystalline diffraction pattern shows a regular pattern of bright spots. This pattern can be seen as a two-dimensional projection of the reciprocal crystal lattice. If there are more contributing crystallites, the diffraction image becomes a superposition of individual crystals' diffraction patterns. Ultimately, this superposition contains diffraction spots of all possible crystallographic plane systems in all possible orientations. This results in a pattern of concentric rings of discrete radii for the following reasons:
- The discreteness of ring radii is given by the fact, that there are discrete spacings between various parallel crystallographic planes in a given crystal system and therefore the beams satisfying the diffraction condition can only form diffraction spots in discrete distances from the transmitted beam.
- The concentricity and ringlike shape is given by the fact, that there are all possible orientations of crystallographic planes and therefore the diffraction spots are formed all around the transmitted beam (rings centre) at the distance (ring radius) corresponding to a particular crystallographic plane.
If the illuminated area selected by the aperture covers many differently oriented crystallites, their diffraction patterns superimpose forming an image of concentric rings. The ring diffraction pattern is typical for polycrystalline samples, powders or nanoparticles. A diameter of each ring corresponds to interplanar distances in the sample. Instead of information about individual grains or sample orientation, this provides statistical information for instance about overall crystallinity or texture. Textured materials can be recognized by a non-uniform distribution of intensity along the ring circumference despite sufficient crystallinity. Ring diffraction patterns can be also used to discriminate between nanocrystalline and amorphous phases.[16]
Multiple materials and double diffraction
In simple cases there is only one grain or one type of material in the area used for collecting a diffraction pattern. However, often there is more than one. If they are in different areas then the diffraction pattern will be a combination. In addition one can have one superimposed on top of another, in which case the electrons that go through the first are diffracted by the second. This leads to diffraction spots which are the sum of those of the two (or even more) crystals, and can lead to quite complicated results.
Convergent Beam Electron Diffraction
Convergent beam electron diffraction (CBED) (see that page's history for attribution) is a diffraction technique where a convergent or divergent beam (conical electron beam) of electrons is used to study materials.
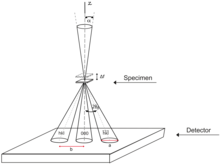
In Convergent Beam Electron Diffraction (CBED), the incident electrons are focused in a converging cone-shaped beam with a crossover often located at the sample, although other methods exist. Unlike the parallel beam, the convergent beam is able to carry information from the sample volume, not just a two-dimensional projection available in SAED. With convergent beam there is also no need for the selected area aperture, as it is inherently site-selective since the beam crossover is positioned to the object plane where the sample is located.[18]
A CBED pattern consists of disks arranged exactly the same as the spots in SAED. Intensity within the disks, however, is not uniform, but represents dynamical diffraction effects and symmetries of the sample structure. Even though the zone axis and lattice parameter analysis based on disk positions does not significantly differ from SAED, the analysis of disks content is significantly more complex. Due to a number of contributing factors, simulation based on dynamical diffraction theory is often required. With appropriate analysis, however, CBED patterns can be used for indexation of the crystal point group, space group identification, measurement of lattice parameters, thickness or strain.[18]
The disk diameter can be controlled using the beam convergence angle. The larger is the angle, the broader the disks are depicting more features. If the angle is increased to certain level, the disks begin to overlap deteriorating the contained information. This can be solved for instance via a large angle convergent electron beam diffraction (LACBED) where the sample is moved upwards or downwards. There are applications, however, where the overlapping disks are beneficial. Ronchigram could serve as an example. It is a CBED pattern, often but not always of an amorphous material, with many intentionally overlapping disks blended into one image providing information about the defects (optical aberration) of the electron optical system.[1]
Precession Electron Diffraction

Precession electron diffraction (PED), first developed by Vincent and Midley in 1994[20] is a specialized method to collect electron diffraction patterns in a transmission electron microscope (TEM), see the main page's history for attribution. By rotating (precessing) a tilted incident electron beam around the central axis of the microscope, a PED pattern is formed which is effectively an integration over a collection of diffraction conditions. This produces a quasi-kinematical diffraction pattern that is more suitable[21] as input into direct methods algorithms using electrons[22] [23] to determine the crystal structure of the sample. Because it avoids many dynamical effects it can also be used to better identify phases.[24]
4D STEM
4D scanning transmission electron microscopy (4D STEM) is a subset of scanning transmission electron microscopy (STEM) methods which utilizes a pixelated electron detector to capture a convergent beam electron diffraction (CBED) pattern at each scan location; see that page's history for attribution. This technique captures a 2 dimensional reciprocal space image associated with each scan point as the beam rasters across a 2 dimensional region in real space, hence the name 4D STEM. Its development was enabled by evolution in STEM detectors and improvements in computational power. The technique has applications in visual diffraction imaging, phase orientation and strain mapping, phase contrast analysis, among others; it has become very popular and rapidly involving from about 2020 onwards.
The name 4D STEM is common in literature, however it is known by other names: 4D STEM EELS, ND STEM (N- since the number of dimensions could be higher than 4), position resolved diffraction (PRD), spatial resolved diffractometry, momentum-resolved STEM, "nanobeam precision electron diffraction", scanning electron nano diffraction, nanobeam electron diffraction, or pixelated STEM.[25]
Low Energy Electron Diffraction(LEED)

Low-energy electron diffraction (LEED) is a technique for the determination of the surface structure of single-crystalline materials by bombardment with a collimated beam of low-energy electrons (30–200 eV)[26] and observation of diffracted electrons as spots on a fluorescent screen; see the orignal page's history for attribution and references[27][28]. It has been used to solve a very large number of relatively simple surface structures of metals and semiconductors, plus cases with simple chemisorbants. For more complex cases transmission electron diffraction[29][30] or surface x-ray diffraction[31] have been used, often with scanning tunnelling microscopy and density functional theory calculations.
LEED may be used in one of two ways:
- Qualitatively, where the diffraction pattern is recorded and analysis of the spot positions gives information on the symmetry of the surface structure. In the presence of an adsorbate the qualitative analysis may reveal information about the size and rotational alignment of the adsorbate unit cell with respect to the substrate unit cell.
- Quantitatively, where the intensities of diffracted beams are recorded as a function of incident electron beam energy to generate the so-called I–V curves. By comparison with theoretical curves, these may provide accurate information on atomic positions on the surface at hand.
Reflection High Energy Electron Diffraction (RHEED)
RHEED, see that page's history for attribution and also references[32] , is a technique used to characterize the surface of crystalline materials. RHEED systems gather information only from the surface layers of the sample, which distinguishes RHEED from other materials characterization methods that also rely on diffraction of high-energy electrons. Transmission electron microscopy, another common electron diffraction method samples mainly the bulk of the sample due to the geometry of the system, although in special cases it can provide surface information[33]. Low-energy electron diffraction (LEED) is also surface sensitive, but LEED achieves surface sensitivity through the use of low energy electrons. The main uses of RHEED to date have been during thin film growth[34], as the geometry is amenable to simultaneous collection of the diffraction data and deposition.
Kikuchi lines

Kikuchi lines are linear features created by electrons scattered both inelastically and elastically. As the electron beam interacts with matter, the electrons are diffracted via elastic scattering, and also scattered inelastically losing part of their kinetic energy. These occur simultaneously, and one cannot separate them -- the Copenhagen interpretation. These electrons form Kikuchi lines which provide information on the orientation.[18]
Kikuchi lines are come in pairs forming Kikuchi bands. They are indexed in terms of the crystallographic planes they are connected to. The angular width of the band is equal to the diffraction angle specified above which means, that in the diffraction pattern, the width of plane will be equal to the distance between transmitted beam and diffraction spot. The position of Kikuchi bands is fixed with respect to each other and the orientation of the sample, but not against the diffraction spots or the direction of the incident electron beam. As the crystal is tilted in the electron beam, the bands move on the diffraction pattern.[18] Kikuchi lines occur in TEM especially in thicker samples, where simultaneous inelastic and elastic scattering occurs. Since the position of Kikuchi bands is quite sensitive to crystal orientation, they can be used to fine-tune a zone-axis orientation. Alternatively, they can be used to determine crystal orientation with significantly higher accuracy than what is feasible with a spot diffraction analysis. Since mutual positions and orientations of Kikuchi bands is fixed with respect to the crystal, and since the bands intersect in low-index zone axes, they can be used for navigation when changing the orientation between zone axes connected by some band. For those purposes, Kikuchi maps are available.[1]
Diffraction by individual molecules in gases

Gas electron diffraction (GED) can be used to determine geometry of molecules dispersed in gases. A gas carrying the molecules is exposed to the electron beam, which is diffracted by the molecules. Since the diffracting molecules are randomly oriented, the resulting diffraction pattern consists of concentric rings. The diffraction intensity is a sum of several components such as background, atomic intensity or molecular intensity.
In GED the diffraction intensities at a particular diffraction angle is described via so-called scattering variable defined as
The total intensity is then given as a sum of partial contributions:
where results from scattering by individual atoms, by pairs of atoms and by atom triplets. Intensity corresponds to the background which, unlike the previous contributions, must be determined experimentally. The intensity of atomic scattering is defined as
where , is the distance between the scattering object detector, is the intensity of the primary electron beam and is the scattering amplitude of the i-th atom in the molecular structure in the experiment. is the main contribution and easily obtained for known gas composition.
The most valuable information is carried by the intensity of molecular scattering , as it contains information about the distance between all pairs of atoms in the molecule, whether bonded or not. It is given by formula
where is the distance between two atoms, is the mean square amplitude of vibration between the two atoms, is the anharmonicity constant and is a phase factor which is important for atomic pairs with very different nuclear charges. The summation is performed over all atom pairs. Atomic triplet intensity is negligible in most cases. If the molecular intensity is extracted from an experimental pattern by subtracting other contributions, it can be used to match and refine a structural model against the experimental data.
In scanning electron microscope

In Scanning electron microscope the region near the surface is mapped using a scanning electron beam. A diffraction pattern is formed using electron backscatter diffraction (EBSD). A region from a few nanometers to a few microns, depending upon the electron energy used, is penetrated by the electrons, some of which are diffracted backwards and out of the sample. As result of combined inelastic and elastic scattering, typical features for an EBSD image are Kikuchi lines. Since the position of Kikuchi bands is highly sensitive to the crystal orientation, EBSD data acquired using the scanning beam can be used to determine the crystal orientation at particular locations on the sample. The data are processed by an automated software allowing to routinely generate two-dimensional orientation maps across the sample surface. As the Kikuchi lines carry information about the interplanar angles and distances and, therefore, about the crystal structure, they can be also used for a phase identification or strain analysis.[35]
See also
- Diffraction
- Selected area diffraction
- Convergent beam electron diffraction
- Electron backscatter diffraction
- Gas electron diffraction
- Low-energy electron diffraction
- Precession Electron Diffraction
- Reflection high-energy electron diffraction
- Ronchigram
- Kikuchi line
- Electron crystallography
- Electron microscope
- Transmission electron microscopy
- Scanning electron microscopy
- CrysTBox
- Microcrystal electron diffraction
- Diffraction
- Crystal structure
- Stereographic projection
- Zone axis
References
- ^ a b c d e Fultz, B (2013). Transmission electron microscopy and diffractometry of materials. Heidelberg New York: Springer. ISBN 978-3-642-43315-3. OCLC 796932144.
- ^ Harsch, Viktor (November 2007). "Otto von Gericke (1602–1686) and his pioneering vacuum experiments". Aviation, Space, and Environmental Medicine. 78 (11): 1075–1077. doi:10.3357/asem.2159.2007. ISSN 0095-6562. PMID 18018443.
- ^ Martin, Andre (1986), "Cathode Ray Tubes for Industrial and Military Applications", in Hawkes, Peter (ed.), Advances in Electronics and Electron Physics, Volume 67, Academic Press, p. 183, ISBN 9780080577333,
Evidence for the existence of "cathode-rays" was first found by Plücker and Hittorf ...
- ^ E. Goldstein (May 4, 1876) "Vorläufige Mittheilungen über elektrische Entladungen in verdünnten Gasen" (Preliminary communications on electric discharges in rarefied gases), Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin (Monthly Reports of the Royal Prussian Academy of Science in Berlin), 279-295. From page 286: "13. Das durch die Kathodenstrahlen in der Wand hervorgerufene Phosphorescenzlicht ist höchst selten von gleichförmiger Intensität auf der von ihm bedeckten Fläche, und zeigt oft sehr barocke Muster." (13. The phosphorescent light that's produced in the wall by the cathode rays is very rarely of uniform intensity on the surface that it covers, and [it] often shows very baroque patterns.)
- ^ Thomson, J. J. (August 1901). "On bodies smaller than atoms". The Popular Science Monthly. Bonnier Corp.: 323–335. Retrieved 2009-06-21.
- ^ Francesco Maria Grimaldi, Physico-mathesis de lumine, coloribus, et iride, aliisque adnexis … [The physical mathematics of light, color, and the rainbow, and other things appended …] (Bologna ("Bonomia"), (Italy): Vittorio Bonati, 1665), pp. 1–11 Archived 2016-12-01 at the Wayback Machine: "Propositio I. Lumen propagatur seu diffunditur non solum directe, refracte, ac reflexe, sed etiam alio quodam quarto modo, diffracte." (Proposition 1. Light propagates or spreads not only in a straight line, by refraction, and by reflection, but also by a somewhat different fourth way: by diffraction.) On p. 187, Grimaldi also discusses the interference of light from two sources: "Propositio XXII. Lumen aliquando per sui communicationem reddit obscuriorem superficiem corporis aliunde, ac prius illustratam." (Proposition 22. Sometimes light, as a result of its transmission, renders dark a body's surface, [which had been] previously illuminated by another [source].)
- ^ "I. The Bakerian Lecture. Experiments and calculations relative to physical optics". Philosophical Transactions of the Royal Society of London. 94. The Royal Society: 1–16. 1804-12-31. doi:10.1098/rstl.1804.0001. ISSN 0261-0523. S2CID 110408369.
- ^ Fresnel, Augustin-Jean (1816), "Mémoire sur la diffraction de la lumière" ("Memoir on the diffraction of light"), Annales de Chimie et de Physique, vol. 1, pp. 239–81 (March 1816); reprinted as "Deuxième Mémoire…" ("Second Memoir…") in Oeuvres complètes d'Augustin Fresnel, vol. 1 (Paris: Imprimerie Impériale, 1866), pp. 89–122. (Revision of the "First Memoir" submitted on 15 October 1815.)
- ^ Fresnel, Augustin-Jean (1818), "Mémoire sur la diffraction de la lumière" ("Memoir on the diffraction of light"), deposited 29 July 1818, "crowned" 15 March 1819, published in Mémoires de l'Académie Royale des Sciences de l'Institut de France, vol. V (for 1821 & 1822, printed 1826), pp. 339–475; reprinted in Oeuvres complètes d'Augustin Fresnel, vol. 1 (Paris: Imprimerie Impériale, 1866), pp. 247–364; partly translated as "Fresnel's prize memoir on the diffraction of light", in H. Crew (ed.), The Wave Theory of Light: Memoirs by Huygens, Young and Fresnel, American Book Company, 1900, pp. 81–144. (First published, as extracts only, in Annales de Chimie et de Physique, vol. 11 (1819), pp. 246–96, 337–78.)
- ^ Christiaan Huygens, Traité de la lumiere … Archived 2016-06-16 at the Wayback Machine (Leiden, Netherlands: Pieter van der Aa, 1690), Chapter 1. From p. 15 Archived 2016-12-01 at the Wayback Machine: "J'ay donc monstré de quelle façon l'on peut concevoir que la lumiere s'etend successivement par des ondes spheriques, … " (I have thus shown in what manner one can imagine that light propagates successively by spherical waves, … ) (Note: Huygens published his Traité in 1690; however, in the preface to his book, Huygens states that in 1678 he first communicated his book to the French Royal Academy of Sciences.)
- ^ De Broglie, Louis (1925). "Recherches sur la théorie des Quanta". Annales de Physique. 10 (3). EDP Sciences: 22–128. Bibcode:1925AnPh...10...22D. doi:10.1051/anphys/192510030022. ISSN 0003-4169.
- ^ Thomson, G. P. (1927). "Diffraction of Cathode Rays by a Thin Film". Nature. 119 (3007): 890. Bibcode:1927Natur.119Q.890T. doi:10.1038/119890a0.
- ^ Ruska, Ernst (1987-08-01). "The development of the electron microscope and of electron microscopy". Bioscience Reports. 7 (8). Portland Press Ltd.: 607–629. doi:10.1007/bf01127674. ISSN 0144-8463. PMID 3322421. S2CID 37346966.
- ^ a b c Klinger, Miloslav (2017-07-07). "More features, more tools, more CrysTBox". Journal of Applied Crystallography. 50 (4). International Union of Crystallography (IUCr): 1226–1234. doi:10.1107/s1600576717006793. ISSN 1600-5767.
- ^ Gjønnes, J.; Moodie, A. F. (1965-07-01). "Extinction conditions in the dynamic theory of electron diffraction". Acta Crystallographica. 19 (1): 65–67. doi:10.1107/S0365110X65002773. ISSN 0365-110X.
- ^ a b c De Graef, Marc (2003-03-27). Introduction to Conventional Transmission Electron Microscopy. Cambridge University Press. doi:10.1017/cbo9780511615092. ISBN 978-0-521-62006-2.
- ^ "Freely available software for electron crystallography and electron microscopy". www.iucr.org/resources/commissions/electron-crystallography/software. IUCr. 2007. Retrieved 8 February 2023.
- ^ a b c d Morniroli, Jean Paul (2004). Large-Angle Convergent-Beam Electron Diffraction Applications to Crystal Defects. Taylor & Francis. doi:10.1201/9781420034073. ISBN 978-2-901483-05-2.
- ^ Own, C. S.: PhD thesis, System Design and Verification of the Precession Electron Diffraction Technique, Northwestern University, 2005,http://www.numis.northwestern.edu/Research/Current/precession.shtml
- ^ Vincent, R.; Midgley, P.A. (1994). "Double conical beam-rocking system for measurement of integrated electron diffraction intensities". Ultramicroscopy. 53 (3): 271–282. doi:10.1016/0304-3991(94)90039-6.
- ^ Gjønnes, J.; Hansen, V.; Berg, B. S.; Runde, P.; Cheng, Y. F.; Gjønnes, K.; Dorset, D. L.; Gilmore, C. J. (1998-05-01). "Structure Model for the Phase AlmFe Derived from Three-Dimensional Electron Diffraction Intensity Data Collected by a Precession Technique. Comparison with Convergent-Beam Diffraction". Acta Crystallographica Section A Foundations of Crystallography. 54 (3): 306–319. doi:10.1107/S0108767397017030.
- ^ Marks, L.D.; Sinkler, W. (2003). "Sufficient Conditions for Direct Methods with Swift Electrons". Microscopy and Microanalysis. 9 (5): 399–410. doi:10.1017/S1431927603030332. ISSN 1431-9276.
- ^ White, T.A.; Eggeman, A.S.; Midgley, P.A. (2010). "Is precession electron diffraction kinematical? Part I:". Ultramicroscopy. 110 (7): 763–770. doi:10.1016/j.ultramic.2009.10.013.
- ^ Moeck, Peter; Rouvimov, Sergei (2010). "Precession electron diffraction and its advantages for structural fingerprinting in the transmission electron microscope". Zeitschrift für Kristallographie. 225 (2–3): 110–124. doi:10.1524/zkri.2010.1162. ISSN 0044-2968.
- ^ "4D STEM | Gatan, Inc". www.gatan.com. Retrieved 2022-03-13.
- ^ K. Oura; V. G. Lifshifts; A. A. Saranin; A. V. Zotov; M. Katayama (2003). Surface Science. Springer-Verlag, Berlin Heidelberg New York. pp. 1–45. ISBN 9783540005452.
- ^ Viefhaus, H. (1987). "Low-energy electron diffraction. Von M. A. Van Hove, W. H. Weinberg und C.-M. Chn. Springer-Verlag Berlin - Heidelberg - New York -London -Paris -Tokyo 1986. XVII, 603 S., 213 Abb., DM 124,-.ISBN 3-540-16262-3". Materials and Corrosion/Werkstoffe und Korrosion (in German). 38 (7): 404–404. doi:10.1002/maco.19870380711. ISSN 0947-5117.
- ^ Moritz, Wolfgang (2022). Surface structure determination by LEED and X-rays. M. A. Van Hove. Cambridge, United Kingdom. ISBN 978-1-108-28457-8. OCLC 1293917727.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Takayanagi, K.; Tanishiro, Y.; Takahashi, M.; Takahashi, S. (1985). "Structural analysis of Si(111)‐7×7 by UHV‐transmission electron diffraction and microscopy". Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films. 3 (3): 1502–1506. doi:10.1116/1.573160. ISSN 0734-2101.
- ^ Gilmore, C.J.; Marks, L.D.; Grozea, D.; Collazo, C.; Landree, E.; Twesten, R.D. (1997). "Direct solutions of the Si(111) 7 × 7 structure". Surface Science. 381 (2–3): 77–91. doi:10.1016/S0039-6028(97)00062-9.
- ^ Robinson, I. K. (1983-04-11). "Direct Determination of the Au(110) Reconstructed Surface by X-Ray Diffraction". Physical Review Letters. 50 (15): 1145–1148. doi:10.1103/PhysRevLett.50.1145. ISSN 0031-9007.
- ^ Ichimiya, Ayahiko (2004). Reflection high-energy electron diffraction. Philip I. Cohen. Cambridge, U.K.: Cambridge University Press. ISBN 0-521-45373-9. OCLC 54529276.
- ^ Kienzle, Danielle M.; Marks, Laurence D. (2012). "Surface transmission electron diffraction for SrTiO3 surfaces". CrystEngComm. 14 (23): 7833. doi:10.1039/c2ce25204j. ISSN 1466-8033.
- ^ Braun, Wolfgang (1999). Applied RHEED : reflection high-energy electron diffraction during crystal growth. Berlin: Springer. ISBN 3-540-65199-3. OCLC 40857022.
- ^ Schwartz, Adam (2009). Electron backscatter diffraction in materials science. New York, NY: Springer. ISBN 978-0-387-88135-5. OCLC 568751820.
External links
- Virtual lab on electron diffraction
- Jmol-mediated image/diffraction analysis of an unknown
- PTCLab-Program for calculation phase transformation crystallography with diffraction simulation, its free and open source python program https://code.google.com/p/transformation-crystallography-lab/
- ronchigram.com Web simulator for generating convergent beam diffraction of amorphous materials.
Further reading
- Diffraction Physics, Cowley, J.M., North-Holland 1995, ISBN 9780080530390. Contains extensive coverage of kinematical and other diffraction.
- Electron microscopy of thin crystals by P. B. Hirsch, A. Howie, R. B. Nicholson, D. W. Pashley and M. J. Whelan, ISBN 9780408185509, often called the bible of electron microscopy
- Electron Microdiffraction, J. C. H. Spence and J. M. Zuo, Springer, 1992, doi:10.1007/978-1-4899-2353-0
- High Energy Electron Diffraction and Microscopy, L.M. Peng, S.L. Dudarev, and M.J. Whelan, Oxford, 2011, ISBN 9780199602247. Extensive coverage of dynamical diffraction.


















![{\displaystyle I_{m}(s)={\frac {K^{2}}{R^{2}}}I_{0}\sum _{i=1}^{N}\sum _{\stackrel {j=1}{i\neq j}}^{N}\left|f_{i}(s)\right|\left|f_{j}(s)\right|{\frac {\sin[s(r_{ij}-\kappa s^{2})]}{sr_{ij}}}e^{-(1/2l_{ij}s^{2})}\cos[\eta _{i}(s)-\eta _{i}(s)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1502d3b423fa3b7b59a79e49b0f2f9e3cd432a4)



