Jump to content

Icosahedral twins: Difference between revisions

Add links
From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
m Ref order and giving proper credit
m A few more improvements
Line 1: Line 1:
{{short description|Structure found in atomic clusters and nanoparticles}}
{{short description|Structure found in atomic clusters and nanoparticles}}
[[File:Twin2.jpg|thumb|[[Transmission electron microscopy]] image of a 5-fold twinned Au nanoparticle with a shape similar to a [[Pentagonal bipyramid]].]]
[[File:Twin2.jpg|thumb|[[Annular dark-field imaging|Annular dark-field image]] of a 5-fold twinned Au nanoparticle with a shape similar to a [[Pentagonal bipyramid]].]]
[[File:IcotwinModel.png|thumb|FCC icosahedralmodel projected down the 5-fold & 3-fold [[zone axis]] orientations.]]
[[File:IcotwinModel.png|thumb|FCC icosahedral model projected down the 5-fold on the left and 3-fold [[zone axis]] orientation on the right.]]
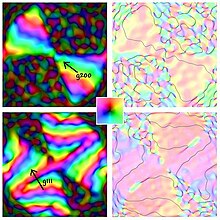
[[File:DigitalDFicotwinExamples.png|thumb|Examples of digital dark field bowtie/butterfly image.]]
[[File:DigitalDFicotwinExamples.png|thumb|Examples of digital dark field bowtie/butterfly images of an icosahedral particle.]]
[[File:Fccicodf.jpg|right|thumb|Dark field analysis of dual-tetrahedron crystal pairs.]]
[[File:Fccicodf.jpg|right|thumb|Dark field analysis of dual-tetrahedron crystal pairs.]]


An '''[[Icosahedron|icosahedral]] [[Crystal twinning|twin]]''' is a nanostructure appearing for atomic [[Cluster (physics)|clusters]] and also nanoparticles with some thousands of atoms. These clusters are twenty-faced, made of twenty interlinked [[tetrahedron|tetrahedra]] crystals, typically joined along triangular (e.g. [[Miller index|cubic-(111)]]) faces having three-fold symmetry. One can think of their formation as a kind of atom-scale [[self-assembly]]. A related, more common structure has five units similarly arranged with twinning, which were known as "fivelings" in the 19th century<ref>{{Cite journal |last=Hofmeister |first=H. |date=1998 |title=Forty Years Study of Fivefold Twinned Structures in Small Particles and Thin Films |url=http://dx.doi.org/10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3 |journal=Crystal Research and Technology |volume=33 |issue=1 |pages=3–25 |doi=10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3 |issn=0232-1300}}
An '''[[Icosahedron|icosahedral]] [[Crystal twinning|twin]]''' is a nanostructure appearing for atomic [[Cluster (physics)|clusters]] and also nanoparticles with some thousands of atoms. These clusters are twenty-faced, made of twenty interlinked [[tetrahedron|tetrahedra]] crystals, typically joined along triangular (e.g. [[Miller index|cubic-(111)]]) faces having three-fold symmetry. One can think of their formation as a kind of atom-scale [[self-assembly]]. A related, more common structure has five units similarly arranged with twinning, which were known as "fivelings" in the 19th century<ref>{{Cite journal |last=Hofmeister |first=H. |date=1998 |title=Forty Years Study of Fivefold Twinned Structures in Small Particles and Thin Films |url=http://dx.doi.org/10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3 |journal=Crystal Research and Technology |volume=33 |issue=1 |pages=3–25 |doi=10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3 |issn=0232-1300}}
</ref><ref name="Hofmeister2004">H. Hofmeister (2004) "Fivefold twinned nanoparticles" in ''Encyclopedia of Nanoscience and Nanotechnology'' (ed. H. S. Nalwa, Amer. Sci. Publ., Stevenson Ranch CA) vol. '''3''', pp. 431-452 {{ISBN|1-58883-059-4}} [https://www-old.mpi-halle.mpg.de/mpi/publi/pdf/5278_04.pdf pdf].</ref><ref>{{Cite journal |last=Marks |first=L D |last2=Peng |first2=L |date=2016-02-10 |title=Nanoparticle shape, thermodynamics and kinetics |url=https://iopscience.iop.org/article/10.1088/0953-8984/28/5/053001 |journal=Journal of Physics: Condensed Matter |volume=28 |issue=5 |pages=053001 |doi=10.1088/0953-8984/28/5/053001 |issn=0953-8984}}</ref>, more recently as "decahedral multiply twinned particles", "pentagonal particles" or "star particles". A variety of different methods (e.g. condensing argon, metal atoms, and [[Capsid|virus capsids]]) lead to icosahedral form on size scales where surface energies are more important those from the bulk.
</ref><ref name="Hofmeister2004">H. Hofmeister (2004) "Fivefold twinned nanoparticles" in ''Encyclopedia of Nanoscience and Nanotechnology'' (ed. H. S. Nalwa, Amer. Sci. Publ., Stevenson Ranch CA) vol. '''3''', pp. 431-452 {{ISBN|1-58883-059-4}} [https://www-old.mpi-halle.mpg.de/mpi/publi/pdf/5278_04.pdf pdf].</ref><ref>{{Cite journal |last=Marks |first=L D |last2=Peng |first2=L |date=2016-02-10 |title=Nanoparticle shape, thermodynamics and kinetics |url=https://iopscience.iop.org/article/10.1088/0953-8984/28/5/053001 |journal=Journal of Physics: Condensed Matter |volume=28 |issue=5 |pages=053001 |doi=10.1088/0953-8984/28/5/053001 |issn=0953-8984}}</ref>, more recently as "decahedral multiply twinned particles", "pentagonal particles" or "star particles". A variety of different methods (e.g. condensing argon, metal atoms, and [[Capsid|virus capsids]]) lead to icosahedral form at size scales where surface energies are more important those from the bulk.


== Causes ==
== Causes ==
When interatom bonding does not have strong directional preferences, it is not unusual for atoms to gravitate toward a [[kissing number]] of 12 nearest neighbors. The three most symmetric ways to do this are by [[Icosahedron|icosahedral]] clustering, or by crystalline [[Cubic crystal system|face-centered-cubic]] ([[Cuboctahedron|cuboctahedral]]) and/or hexagonal (tri-[[Bicupola (geometry)|orthobicupolar]]) [[close packing]].
When interatom bonding does not have strong directional preferences, it is not unusual for atoms to gravitate toward a [[kissing number]] of 12 nearest neighbors. The three most symmetric ways to do this are by [[Icosahedron|icosahedral]] clustering, or by crystalline [[Cubic crystal system|face-centered-cubic]] ([[Cuboctahedron|cuboctahedral]]) and/or hexagonal (tri-[[Bicupola (geometry)|orthobicupolar]]) [[close packing]].


Icosahedral arrangements, typically because of their smaller surface area and surface energy<ref name=Ino1>{{Cite journal |last=Ino |first=Shozo |date=October 1969 |title=Stability of Multiply-Twinned Particles |url=http://dx.doi.org/10.1143/jpsj.27.941 |journal=Journal of the Physical Society of Japan |volume=27 |issue=4 |pages=941–953 |doi=10.1143/jpsj.27.941 |issn=0031-9015}}</ref>, may be preferred for small clusters. However, the Achilles heel for icosahedral clustering is that it cannot fill space over large distances in a way that is translationally ordered, so there is some distortion of the atomic positions, that is elastic strain<ref name=Ino1/> which DeWit pointed out can be thought of in terms of [[Disclination|Disclinations]]<ref>{{Cite journal |last=Wit |first=R de |date=1972-03-14 |title=Partial disclinations |url=https://iopscience.iop.org/article/10.1088/0022-3719/5/5/004 |journal=Journal of Physics C: Solid State Physics |volume=5 |issue=5 |pages=529–534 |doi=10.1088/0022-3719/5/5/004 |issn=0022-3719}}</ref>, an approach later extended to 3D by Yoffe<ref>{{Cite journal |last=Howie |first=A. |last2=Marks |first2=L. D. |date=1984 |title=Elastic strains and the energy balance for multiply twinned particles |url=http://www.tandfonline.com/doi/abs/10.1080/01418618408233432 |journal=Philosophical Magazine A |language=en |volume=49 |issue=1 |pages=95–109 |doi=10.1080/01418618408233432 |issn=0141-8610}}</ref>
Icosahedral arrangements, typically because of their smaller [[Surface energy]]<ref name=Ino1>{{Cite journal |last=Ino |first=Shozo |date=October 1969 |title=Stability of Multiply-Twinned Particles |url=http://dx.doi.org/10.1143/jpsj.27.941 |journal=Journal of the Physical Society of Japan |volume=27 |issue=4 |pages=941–953 |doi=10.1143/jpsj.27.941 |issn=0031-9015}}</ref>, may be preferred for small clusters. However, the [[Achilles' heel]] for icosahedral clustering is that it cannot fill space over large distances in a way that is translationally ordered, so there is some distortion of the atomic positions, that is elastic strain<ref name=Ino1/> which DeWit pointed out can be thought of in terms of [[Disclination|Disclinations]]<ref>{{Cite journal |last=Wit |first=R de |date=1972-03-14 |title=Partial disclinations |url=https://iopscience.iop.org/article/10.1088/0022-3719/5/5/004 |journal=Journal of Physics C: Solid State Physics |volume=5 |issue=5 |pages=529–534 |doi=10.1088/0022-3719/5/5/004 |issn=0022-3719}}</ref>, an approach later extended to 3D by Yoffe.<ref>{{Cite journal |last=Howie |first=A. |last2=Marks |first2=L. D. |date=1984 |title=Elastic strains and the energy balance for multiply twinned particles |url=http://www.tandfonline.com/doi/abs/10.1080/01418618408233432 |journal=Philosophical Magazine A |language=en |volume=49 |issue=1 |pages=95–109 |doi=10.1080/01418618408233432 |issn=0141-8610}}</ref> The shape is also not always that of a simple icosahedron, and there are now several software codes that make it easy to calculate these, for instance references.<ref>{{Cite journal |last=Boukouvala |first=Christina |last2=Daniel |first2=Joshua |last3=Ringe |first3=Emilie |date=2021-09-09 |title=Approaches to modelling the shape of nanocrystals |url=https://nanoconvergencejournal.springeropen.com/articles/10.1186/s40580-021-00275-6 |journal=Nano Convergence |language=en |volume=8 |issue=1 |pages=26 |doi=10.1186/s40580-021-00275-6 |issn=2196-5404 |pmc=PMC8429535 |pmid=34499259}}</ref><ref>{{Cite journal |last=Rahm |first=J. |last2=Erhart |first2=Paul |date=2020-01-07 |title=WulffPack: A Python package for Wulff constructions |url=https://joss.theoj.org/papers/10.21105/joss.01944 |journal=Journal of Open Source Software |volume=5 |issue=45 |pages=1944 |doi=10.21105/joss.01944 |issn=2475-9066}}</ref>


Hence bulk materials (i.e. sufficiently large clusters) generally revert to one of the crystalline close-packing configurations instead. In other words, when icosahedral clusters get sufficiently large, the bulk-atom vote wins out over the surface-atom vote, and the nanoparticles can reduce their energy by converting to simple [[Single crystal]] with a [[Wulff construction]]<ref>{{Cite book |last=Pimpinelli |first=Alberto |url=https://www.cambridge.org/core/product/identifier/9780511622526/type/book |title=Physics of Crystal Growth |last2=Villain |first2=Jacques |date=1998-12-10 |publisher=Cambridge University Press |isbn=978-0-521-55198-4 |edition=1 |doi=10.1017/cbo9780511622526}}</ref> shape. This occurs typically in the range where the particles are 10-30 [[Nanometre|Nanometers]] in diameter<ref>{{Cite journal |last=Baletto |first=Francesca |last2=Ferrando |first2=Riccardo |date=2005-05-24 |title=Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects |url=https://link.aps.org/doi/10.1103/RevModPhys.77.371 |journal=Reviews of Modern Physics |language=en |volume=77 |issue=1 |pages=371–423 |doi=10.1103/RevModPhys.77.371 |issn=0034-6861}}</ref>, but it does not always happen and the particles can grow to millimeter sizes.
At larger sizes the energy to distort becomes larger than the gain in surface energy, and bulk materials (i.e. sufficiently large clusters) generally revert to one of the crystalline close-packing configurations instead. In other words, when icosahedral clusters get sufficiently large, the bulk-atom vote wins out over the surface-atom vote, and the nanoparticles can reduce their energy by converting to simple [[Single crystal]] with a [[Wulff construction]]<ref>{{Cite book |last=Pimpinelli |first=Alberto |url=https://www.cambridge.org/core/product/identifier/9780511622526/type/book |title=Physics of Crystal Growth |last2=Villain |first2=Jacques |date=1998-12-10 |publisher=Cambridge University Press |isbn=978-0-521-55198-4 |edition=1 |doi=10.1017/cbo9780511622526}}</ref> shape. This occurs typically in the range where the particles are 10-30 [[Nanometre|Nanometers]] in diameter<ref>{{Cite journal |last=Baletto |first=Francesca |last2=Ferrando |first2=Riccardo |date=2005-05-24 |title=Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects |url=https://link.aps.org/doi/10.1103/RevModPhys.77.371 |journal=Reviews of Modern Physics |language=en |volume=77 |issue=1 |pages=371–423 |doi=10.1103/RevModPhys.77.371 |issn=0034-6861}}</ref>, but it does not always happen and the particles can grow to millimeter sizes.


== Ubiquity ==
== Ubiquity ==

Revision as of 17:55, 12 February 2023

Annular dark-field image of a 5-fold twinned Au nanoparticle with a shape similar to a Pentagonal bipyramid.
FCC icosahedral model projected down the 5-fold on the left and 3-fold zone axis orientation on the right.
Examples of digital dark field bowtie/butterfly images of an icosahedral particle.
Dark field analysis of dual-tetrahedron crystal pairs.

An icosahedral twin is a nanostructure appearing for atomic clusters and also nanoparticles with some thousands of atoms. These clusters are twenty-faced, made of twenty interlinked tetrahedra crystals, typically joined along triangular (e.g. cubic-(111)) faces having three-fold symmetry. One can think of their formation as a kind of atom-scale self-assembly. A related, more common structure has five units similarly arranged with twinning, which were known as "fivelings" in the 19th century[1][2][3], more recently as "decahedral multiply twinned particles", "pentagonal particles" or "star particles". A variety of different methods (e.g. condensing argon, metal atoms, and virus capsids) lead to icosahedral form at size scales where surface energies are more important those from the bulk.

Causes

When interatom bonding does not have strong directional preferences, it is not unusual for atoms to gravitate toward a kissing number of 12 nearest neighbors. The three most symmetric ways to do this are by icosahedral clustering, or by crystalline face-centered-cubic (cuboctahedral) and/or hexagonal (tri-orthobicupolar) close packing.

Icosahedral arrangements, typically because of their smaller Surface energy[4], may be preferred for small clusters. However, the Achilles' heel for icosahedral clustering is that it cannot fill space over large distances in a way that is translationally ordered, so there is some distortion of the atomic positions, that is elastic strain[4] which DeWit pointed out can be thought of in terms of Disclinations[5], an approach later extended to 3D by Yoffe.[6] The shape is also not always that of a simple icosahedron, and there are now several software codes that make it easy to calculate these, for instance references.[7][8]

At larger sizes the energy to distort becomes larger than the gain in surface energy, and bulk materials (i.e. sufficiently large clusters) generally revert to one of the crystalline close-packing configurations instead. In other words, when icosahedral clusters get sufficiently large, the bulk-atom vote wins out over the surface-atom vote, and the nanoparticles can reduce their energy by converting to simple Single crystal with a Wulff construction[9] shape. This occurs typically in the range where the particles are 10-30 Nanometers in diameter[10], but it does not always happen and the particles can grow to millimeter sizes.

Ubiquity

Icosahedral twinning has been seen in face-centered-cubic metal nanoparticles that have nucleated: (i) by evaporation onto surfaces, (ii) out of solution, and (iii) by reduction in a polymer matrix.

Quasicrystals are un-twinned structures with long range rotational but not translational periodicity, that some initially tried to explain away as icosahedral twinning.[11] Quasi-crystals let non-space-filling coordination persist to larger size scales. However, they generally form only when the compositional makeup (e.g. of two dissimilar metals like Ti and Mn) serves as an antagonist to formation of one of the more common close-packed space-filling but twinned crystalline forms.

See also

Footnotes

  1. ^ Hofmeister, H. (1998). <3::aid-crat3>3.0.co;2-3 "Forty Years Study of Fivefold Twinned Structures in Small Particles and Thin Films". Crystal Research and Technology. 33 (1): 3–25. doi:10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3. ISSN 0232-1300.
  2. ^ H. Hofmeister (2004) "Fivefold twinned nanoparticles" in Encyclopedia of Nanoscience and Nanotechnology (ed. H. S. Nalwa, Amer. Sci. Publ., Stevenson Ranch CA) vol. 3, pp. 431-452 ISBN 1-58883-059-4 pdf.
  3. ^ Marks, L D; Peng, L (2016-02-10). "Nanoparticle shape, thermodynamics and kinetics". Journal of Physics: Condensed Matter. 28 (5): 053001. doi:10.1088/0953-8984/28/5/053001. ISSN 0953-8984.
  4. ^ a b Ino, Shozo (October 1969). "Stability of Multiply-Twinned Particles". Journal of the Physical Society of Japan. 27 (4): 941–953. doi:10.1143/jpsj.27.941. ISSN 0031-9015.
  5. ^ Wit, R de (1972-03-14). "Partial disclinations". Journal of Physics C: Solid State Physics. 5 (5): 529–534. doi:10.1088/0022-3719/5/5/004. ISSN 0022-3719.
  6. ^ Howie, A.; Marks, L. D. (1984). "Elastic strains and the energy balance for multiply twinned particles". Philosophical Magazine A. 49 (1): 95–109. doi:10.1080/01418618408233432. ISSN 0141-8610.
  7. ^ Boukouvala, Christina; Daniel, Joshua; Ringe, Emilie (2021-09-09). "Approaches to modelling the shape of nanocrystals". Nano Convergence. 8 (1): 26. doi:10.1186/s40580-021-00275-6. ISSN 2196-5404. PMC 8429535. PMID 34499259.{{cite journal}}: CS1 maint: PMC format (link) CS1 maint: unflagged free DOI (link)
  8. ^ Rahm, J.; Erhart, Paul (2020-01-07). "WulffPack: A Python package for Wulff constructions". Journal of Open Source Software. 5 (45): 1944. doi:10.21105/joss.01944. ISSN 2475-9066.
  9. ^ Pimpinelli, Alberto; Villain, Jacques (1998-12-10). Physics of Crystal Growth (1 ed.). Cambridge University Press. doi:10.1017/cbo9780511622526. ISBN 978-0-521-55198-4.
  10. ^ Baletto, Francesca; Ferrando, Riccardo (2005-05-24). "Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects". Reviews of Modern Physics. 77 (1): 371–423. doi:10.1103/RevModPhys.77.371. ISSN 0034-6861.
  11. ^ Pauling, Linus (1987-01-26). "So-called icosahedral and decagonal quasicrystals are twins of an 820-atom cubic crystal". Physical Review Letters. 58 (4). American Physical Society (APS): 365–368. doi:10.1103/physrevlett.58.365. ISSN 0031-9007.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Icosahedral_twins&oldid=1138970732"