Schönhardt polyhedron: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
source Cauchy
Line 26: Line 26:


===Jumping polyhedron===
===Jumping polyhedron===
In connection with the theory of [[flexible polyhedron|flexible polyhedra]], some instances of the Schönhardt polyhedron form a "jumping polyhedron": a polyhedron that has two different rigid states, both having the same face shapes and the same orientation (convex or concave) of each edge. A model whose surface is made of a stiff but somewhat deformable material, such as cardstock, can be made to "jump" between the two shapes. A solid model could not change shape in this way. Neither could a model made of a more rigid material like glass: although it could exist in either of the two shapes, it would be unable to deform sufficiently to move between them. This stands in contrast to [[Cauchy's theorem (geometry)|Cauchy's rigidity theorem]], according to which, for each [[convex polyhedron]], there is no other polyhedron having the same face shapes and edge orientations.{{r|grunbaum}}
In connection with the theory of [[flexible polyhedron|flexible polyhedra]], some instances of the Schönhardt polyhedron form a "jumping polyhedron": a polyhedron that has two different rigid states, both having the same face shapes and the same orientation (convex or concave) of each edge. A model whose surface is made of a stiff but somewhat deformable material, such as cardstock, can be made to "jump" between the two shapes. A solid model could not change shape in this way. Neither could a model made of a more rigid material like glass: although it could exist in either of the two shapes, it would be unable to deform sufficiently to move between them.{{r|grunbaum}} This stands in contrast to [[Cauchy's theorem (geometry)|Cauchy's rigidity theorem]], according to which, for each [[convex polyhedron]], there is no other polyhedron having the same face shapes and edge orientations. As well as jumping, non-convex polyhedra can be [[flexible polyhedron|flexible]], having a continuous family of shapes with the same faces.{{r|az}}


In his original work on this polyhedron, Schönhardt noted a related property: in one special form, when the two equilateral faces are twisted at an angle of 30° with respect to each other, this polyhedron becomes "shaky": rigid with respect to continuous motion, but not [[Structural rigidity|infinitesimally rigid]].{{r|schonhardt}}
In his original work on this polyhedron, Schönhardt noted a related property: in one special form, when the two equilateral faces are twisted at an angle of 30° with respect to each other, this polyhedron becomes "shaky": rigid with respect to continuous motion, but not [[Structural rigidity|infinitesimally rigid]].{{r|schonhardt}}
Line 43: Line 43:
== References ==
== References ==
{{reflist|refs=
{{reflist|refs=

<ref name=az>{{citation
| last1 = Aigner | first1 = Martin | author1-link = Martin Aigner
| last2 = Ziegler | first2 = Günter M. | author2-link = Günter M. Ziegler
| contribution = Chapter 14: Cauchy's rigidity theorem
| doi = 10.1007/978-3-662-57265-8_15
| edition = 6th
| isbn = 978-3-662-57265-8
| pages = 95-98
| publisher = Springer
| title = Proofs from THE BOOK
| title-link = Proofs from THE BOOK
| year = 2018}}</ref>


<ref name=bagemihl>{{citation
<ref name=bagemihl>{{citation

Revision as of 19:49, 19 February 2024

Schönhardt polyhedron
Faces8
Edges12
Vertices6
PropertiesCannot be triangulated
Net
3D model of the Schönhardt polyhedron

In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. It is the simplest polyhedron that cannot be triangulated into tetrahedra without adding new vertices. It is named after German mathematician Erich Schönhardt, who described it in 1928.[1] The same polyhedra have also been studied in connection with Cauchy's rigidity theorem as an example where polyhedra with two different shapes have faces of the same shapes.

Construction

One way of constructing a Schönhardt polyhedron starts with a triangular prism, with two parallel equilateral triangles as its faces. One of the triangles is rotated around the centerline of the prism, breaking the square faces of the prism into pairs of triangles. If each pair of triangles is chosen to have a non-convex dihedral angle, the Schönhardt polyhedron is the result.[2]

Properties

Each Schönhardt polyhedron has six vertices, twelve edges, and eight triangular faces. The six vertices of the Schönhardt polyhedron can be used to form fifteen unordered pairs of vertices. Twelve of these fifteen pairs form edges of the polyhedron: there are six edges in the two equilateral triangle faces, and six edges connecting the two triangles. The remaining three edges form diagonals of the polyhedron, but lie entirely outside the polyhedron.[3]

The convex hull of the Schönhardt polyhedron is another polyhedron with the same six vertices, and a different set of twelve edges and eight triangular faces. Both this hull, and the Schönhardt polyhedron itself, are combinatorially equivalent to a regular octahedron. The symmetric difference of the hull and the Schönhardt polyhedron consists of three tetrahedra, each lying between one of the concave dihedral edges of the Schönhardt polyhedron and one of the exterior diagonals. Thus, the Schönhardt polyhedron can be formed by removing these three tetrahedra from a convex (but irregular) octahedron.[4]

Impossibility of triangulation

It is impossible to partition the Schönhardt polyhedron into tetrahedra whose vertices are vertices of the polyhedron. More strongly, there is no tetrahedron that lies entirely inside the Schönhardt polyhedron and has vertices of the polyhedron as its four vertices. This follows from the following two properties of the Schönhardt polyhedron:[3]

  • Every triangle formed by its edges is one of its faces. Therefore, because it is not a tetrahedron itself, every tetrahedron formed by four of its vertices must have an edge that it does not share with the Schönhardt polyhedron.[3]
  • Every diagonal that connects two of its vertices but is not an edge of the Schönhardt polyhedron lies outside the polyhedron. Therefore, every tetrahedron that uses such a diagonal as one of its edges must also lie in part outside the Schönhardt polyhedron.[3]

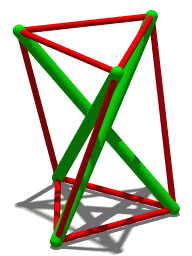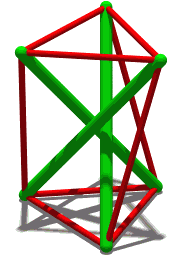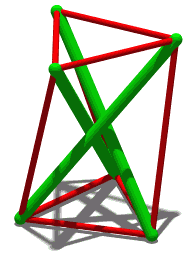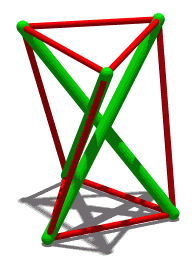
Jumping polyhedron

In connection with the theory of flexible polyhedra, some instances of the Schönhardt polyhedron form a "jumping polyhedron": a polyhedron that has two different rigid states, both having the same face shapes and the same orientation (convex or concave) of each edge. A model whose surface is made of a stiff but somewhat deformable material, such as cardstock, can be made to "jump" between the two shapes. A solid model could not change shape in this way. Neither could a model made of a more rigid material like glass: although it could exist in either of the two shapes, it would be unable to deform sufficiently to move between them.[5] This stands in contrast to Cauchy's rigidity theorem, according to which, for each convex polyhedron, there is no other polyhedron having the same face shapes and edge orientations. As well as jumping, non-convex polyhedra can be flexible, having a continuous family of shapes with the same faces.[6]

In his original work on this polyhedron, Schönhardt noted a related property: in one special form, when the two equilateral faces are twisted at an angle of 30° with respect to each other, this polyhedron becomes "shaky": rigid with respect to continuous motion, but not infinitesimally rigid.[1]

Related constructions

Schönhardt's 1928 discovery of this polyhedron was prompted by earlier work of Nels Johann Lennes, who published in 1911 a seven-vertex polyhedron with no triangulation.[1][7][8]

It was shown by Rambau (2005) that the Schönhardt polyhedron can be generalized to other polyhedra, combinatorially equivalent to antiprisms, that cannot be triangulated. These polyhedra are formed by connecting regular k-gons in two parallel planes, twisted with respect to each other, in such a way that k of the 2k edges that connect the two k-gons have concave dihedrals. For sufficiently small twisting angles, the result has no triangulation.[4][9] Another polyhedron that cannot be triangulated is Jessen's icosahedron, which is combinatorially equivalent to a regular icosahedron,[2] and (like the degenerate form of Schönhardt's polyhedron) also shaky.[10]

In a different direction, Bagemihl (1948) constructed a polyhedron that shares with the Schönhardt polyhedron the property that it has no internal diagonals. The tetrahedron and the Császár polyhedron have no diagonals at all: every pair of vertices in these polyhedra forms an edge.[3] It remains an open question whether there are any other polyhedra (with manifold boundary) without diagonals,[11] although there exist non-manifold surfaces with no diagonals and any number of vertices greater than five.[12]

Applications

Schönhardt's polyhedron resembles the simplest tensegrity structure with three compression (green) and nine tension (red) members.[13]

Ruppert & Seidel (1992) used Schönhardt's polyhedron as the basis for a proof that it is NP-complete to determine whether a non-convex polyhedron can be triangulated. The proof uses many copies of the Schönhardt polyhedron, with its top face removed, as gadgets within a larger polyhedron. Any triangulation of the overall polyhedron must include a tetrahedron connecting the bottom face of each gadget to a vertex in the rest of the polyhedron that can see this bottom face. The complex pattern of obstructions between tetrahedra of this type can be used to simulate Boolean logic components in a reduction from the Boolean satisfiability problem.[4][14]

References

  1. ^ a b c Schönhardt, E. (1928), "Über die Zerlegung von Dreieckspolyedern in Tetraeder", Mathematische Annalen, 98: 309–312, doi:10.1007/BF01451597
  2. ^ a b Bezdek, Andras; Carrigan, Braxton (2016), "On nontriangulable polyhedra", Beiträge zur Algebra und Geometrie, 57 (1): 51–66, doi:10.1007/s13366-015-0248-4, MR 3457762, S2CID 118484882
  3. ^ a b c d e Bagemihl, F. (1948), "On indecomposable polyhedra", American Mathematical Monthly, 55 (7): 411–413, doi:10.2307/2306130, JSTOR 2306130
  4. ^ a b c De Loera, Jesús A.; Rambau, Jörg; Santos, Francisco (2010), "Example 3.6.1: Schönhardt's polyhedron", Triangulations: Structures for algorithms and applications, Algorithms and Computation in Mathematics, vol. 25, Berlin: Springer-Verlag, pp. 133–134, doi:10.1007/978-3-642-12971-1, ISBN 978-3-642-12970-4, MR 2743368
  5. ^ Grünbaum, Branko (1975), Lectures on lost mathematics (PDF), pp. 41–42
  6. ^ Aigner, Martin; Ziegler, Günter M. (2018), "Chapter 14: Cauchy's rigidity theorem", Proofs from THE BOOK (6th ed.), Springer, pp. 95–98, doi:10.1007/978-3-662-57265-8_15, ISBN 978-3-662-57265-8
  7. ^ Lennes, N. J. (January 1911), "Theorems on the simple finite polygon and polyhedron", American Journal of Mathematics, 33 (1/4): 37–62, JSTOR 2369986
  8. ^ "Model of a Lennes Polyhedron By Richard P. Baker, Baker #287", Collections, National Museum of American History, retrieved 2024-02-18
  9. ^ Rambau, J. (2005), "On a generalization of Schönhardt's polyhedron" (PDF), in Goodman, Jacob E.; Pach, János; Welzl, Emo (eds.), Combinatorial and Computational Geometry, MSRI Publications, vol. 52, Cambridge: Cambridge University Press, pp. 501–516
  10. ^ Goldberg, Michael (1978), "Unstable polyhedral structures", Mathematics Magazine, 51 (3): 165–170, doi:10.2307/2689996, JSTOR 2689996, MR 0498579
  11. ^ Ziegler, Günter M. (2008), "Polyhedral surfaces of high genus", in Bobenko, A. I.; Schröder, P.; Sullivan, J. M.; et al. (eds.), Discrete Differential Geometry, Oberwolfach Seminars, vol. 38, Springer-Verlag, pp. 191–213, arXiv:math/0412093, doi:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7, math.MG/0412093
  12. ^ Szabó, Sándor (1984), "Polyhedra without diagonals", Periodica Mathematica Hungarica, 15 (1): 41–49, doi:10.1007/BF02109370; Szabó, Sándor (2009), "Polyhedra without diagonals II", Periodica Mathematica Hungarica, 58 (2): 181–187, doi:10.1007/s10998-009-10181-x
  13. ^ Tobie, Roger (2012), "What Can You Learn From a Hole in the Ground?", Proceeding of the Natural Philosophy Alliance, 19th Annual Conference, 25-28 July, 2012, Albquerque, New Mexico, vol. 9, Lulu Press, p. 628, ISBN 978-1-105-95509-9
  14. ^ Ruppert, J.; Seidel, R. (1992), "On the difficulty of triangulating three-dimensional nonconvex polyhedra", Discrete & Computational Geometry, 7: 227–253, doi:10.1007/BF02187840

External links

Retrieved from "https://en.wikipedia.org/w/index.php?title=Schönhardt_polyhedron&oldid=1208983796"