Penrose tiling

A Penrose tiling.

A Penrose tiling is a nonperiodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. Because all tilings obtained with the Penrose tiles are non-periodic, Penrose tilings are considered aperiodic tilings. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right.

A Penrose tiling has many remarkable properties, most notably:

• It is nonperiodic, which means that it lacks any translational symmetry. More informally, a shifted copy will never match the original exactly.
• Any finite region in a tiling appears infinitely many times in that tiling and, in fact, in any other tiling. This property would be trivially true of a tiling with translational symmetry but is non-trivial when applied to the non-periodic Penrose tilings.
• It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction; the diffractogram reveals both the underlying fivefold symmetry and the long range order. This order reflects the fact that the tilings are organized, not through translational symmetry, but rather through a process sometimes called "deflation" or "inflation."

Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions, cut and project schemes and coverings.

Historical background

The sets of tiles proposed by Penrose are among the most simple examples of a counter-intuitive mathematical fact - the existence of aperiodic sets. In 1961, Hao Wang noted connections between problems in geometry—specifically problems about tiling—and a certain class of decision problem. As an aside, he observed that if the so-called Domino Problem were undecidable, then there would have to exist an aperiodic set of tiles. As the existence of such a set seemed implausible, Wang conjectured no such set could exist, and that the Domino Problem is decidable for tiles in the plane.

In his 1964 thesis, Robert Berger disproved Wang's conjecture, proving that the Domino Problem is in fact undecidable, and producing an aperiodic set of 104 distinct tiles. (In his published monograph, Berger gives only a larger set of 20426 tiles.)

This number was further reduced by Donald Knuth, Hans Läuchli and then Raphael Robinson, who gave an aperiodic set of just six tiles (and simplified Berger's proof) in a 1971 paper. In 1972, Roger Penrose gave the first of several variations of tiles forcing a hierarchical pentagonal structure, a set of six tiles (tiling P1 below). Penrose subsequently reduced the number of distinct tiles required to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below). The rhombus tiling was independently discovered by Robert Ammann in 1976. Penrose and John H. Conway investigated the properties of Penrose tilings and their findings were publicized by Martin Gardner in his January 1977 "Mathematical Games" column in Scientific American.

In 1981 De Bruijn explained a method to construct Penrose tilings from five families of parallel lines as well as a "cut and project method", in which Penrose tilings are obtained as two-dimensional projections from a five-dimensional cubic structure. In this approach the Penrose tiling is considered as a set of points, its vertices, while its tiles are just the geometrical shapes defined by connecting edges.

The original Penrose tiling (P1)

A tiling constructed from Penrose's original (P1) set of six tiles.

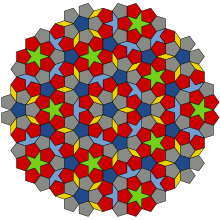
The original Penrose tiling was proposed in 1974 in a paper entitled the Role of aesthetics in pure and applied research. Penrose acknowledged inspiration from the work of Johannes Kepler. In his book Harmonices Mundi Kepler explored tilings built around pentagons and it was shown that his construction can be extended into a Penrose tiling. Earlier traces of this idea have been traced to Dürer's work.

Attempting to tile the plane with regular pentagons must necessarily leave gaps. Penrose found a particular tiling in which the gaps may be filled with three other shapes: a star, a boat and a diamond, as shown on the left. In addition to the tiles, Penrose stated rules, usually called matching rules, that specify how tiles must be attached to one another; these rules are needed to ensure that the tilings are nonperiodic. As there are three distinct sets of matching rules for pentagonal tiles, it is common to consider the set as having three different pentagonal tiles, shown in different colors in the illustration. This leads to a set of six tiles: a thin rhombus or 'diamond', a five pointed star, a 'boat' (roughly 3/5 of a star) and three pentagons.

The pentagonal Penrose tiling (P1) in black on a colored rhombus tiling (P3) background.

Penrose later found two more sets of aperiodic tiles, one consisting of tiles known as a 'kite' and a 'dart' (P2) and a second set consisting of two rhombuses (P3). The correspondence between a P1 tiling and a P3 tiling is illustrated to the right.

Kite and dart tiling (P2)

The quadrilaterals called the 'Kite' and 'Dart' can also be used to form a Penrose tiling.

Kite and Dart tiles

• The Kite is a quadrilateral whose four corners have angles of 72, 72, 72, and 144 degrees. The Kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles.
• The Dart is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The Dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles.

The green and the red arcs in the tiles constrain the placement of tiles: When two tiles share an edge in a tiling, the patterns must match at these edges. For example, the concave vertex of a Dart cannot be filled with a single Kite to create a rhombus, but must be filled with a pair of Kites.

Rhombus tiling (P3)

The Penrose rhombuses are a pair of rhombuses with equal sides but different angles.

Two kinds of matching rules for Penrose rhombuses.

• The thin rhombus t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhombus may be bisected along its short diagonal to form a pair of acute Robinson triangles.
• The thick rhombus T has angles of 72, 108, 72, and 108 degrees. The T rhombus may be bisected along its long diagonal to form a pair of obtuse Robinson triangles.

There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only 7 of these combinations to appear. Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled. The simplest rule, prohibiting two tiles to be put together to form a single parallelogram, is insufficient to ensure aperiodicity. Instead, rules are made that distinguish sides of the tiles and require that only particular sides can be put together with each other. An example of appropriate matching rules is shown in the upper part of the diagram to the left. Tiles must be assembled so that the curves across their edges match in color and position. An equivalent condition is that tiles must be assembled so that the bumps on their edges fit together. The same rules can be specified with other formulations.

There are arbitrarily large finite patches with tenfold symmetry and at most one center point of global tenfold symmetry where ten mirror lines cross. As the tiling is aperiodic, there is no translational symmetry—the pattern cannot be shifted to match itself over the entire plane. However, any bounded region, no matter how large, will be repeated an infinite number of times within the tiling. Therefore, a finite patch cannot differentiate between the uncountably many Penrose tilings, nor even determine which position within the tiling is being shown. The only way to distinguish the two symmetric Penrose tilings from the others is that their symmetry continues to infinity.

The rhombuses may be cut in half to form a pair of triangles, called Robinson triangles, which can be used to produce the Penrose tilings as a substitution tiling. The Robinson triangles are the isosceles 36º-36º-108º and 72º-72º-36º triangles. Each of these triangles has edges in the ratio of (1+√5):2, the golden ratio φ.

Deflation

A substitution method known as deflation, the steps of which are described below, will produce a kite and dart (P2) Penrose tiling. Starting with a finite tiling called the axiom, deflation proceeds with a sequence of steps called generations. The axiom can be as simple as a single tile. In one generation of deflation, each tile is replaced with one or more new tiles that exactly cover the area of the original tile. The new tiles are scaled-down versions of the original tiles. The substitution rules guarantee that the new tiles are arranged according to the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles. Given sufficiently many generations, the tiling will contain a scaled-down version of the axiom that does not touch the boundary of the tiling. The axiom can then be surrounded by full-size tiles corresponding to tiles that appear in the scaled-down version. This extended tiling can be used as a new axiom, producing larger and larger extended tilings and ultimately covers the entire plane.

An example: three generations of four axioms

This is an example of successive generations of deflation starting from different axioms. In the case of the 'Sun' and 'Star', the scaled-down interior version of the axiom appears in generation 2. The 'Sun' also appears in the interior of its generation 3.

Name	Generation 0 (or axiom)	Generation 1	Generation 2	Generation 3
Kite (half)
Dart (half)
Sun
Star

Decagonal covering

Gummelt's decagon and the two kinds of overlap.

In 1996, German mathematician Petra Gummelt demonstrated that a covering equivalent to the Penrose tiling can be built by covering the plane with a single decagonal tile if two kinds of overlap are allowed (it is called a covering to distinguish it from a non-overlapping tiling). The decagonal tile is decorated with colored patches and the covering rule only allows overlaps compatible with the coloring.

A decomposition of the decagonal tile into kites and darts transforms such a covering into a Penrose tiling. If a fat 'T' rhombus is inscribed into each decagon, that part of the Penrose tiling corresponding to these shapes is obtained, while places for thin tiles are left unoccupied. In the covering method, different atomic clusters share the fragments from which the aperiodic structure is built. The overlapping decagons are seen as "quasi-unit cells" analogous to the unit cells from which crystals are constructed; this is considered to be a realistic model for the growth of quasicrystals.

Golden ratio features

Length ratios in Penrose tiles.

Several properties and features of the Penrose tiling involve the golden ratio φ. This is a consequence of the local fivefold rotational symmetry of the tiling and the fact that the ratio of chord lengths to side lengths in a regular pentagon is φ. The ratio of the lengths of long sides to short sides in the isosceles Robinson triangles is φ:1. As a result, the ratio of the lengths of long sides to short sides in the kite and dart tiles, the ratio of the areas of the kite and dart tiles, the ratio of the lengths of sides to short diagonal in the thin rhombus and the ratio of lengths of long diagonal to sides in the thick rhombus are all φ:1.

The deflation construction decomposes a kite into two kites and a dart, and decomposes a dart into a kite and a dart. The number of kites and darts in the nth iteration of the construction is determined by the nth power of the substitution matrix:

${\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}={\begin{pmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n-1}\end{pmatrix}}\,,$

where F_n is the nth Fibonacci number. The ratio of numbers of kites to darts in any sufficiently large P2 Penrose tiling pattern therefore tends to φ. A similar result holds for the ratio of the number of thick rhombuses to thin rhombuses in the P3 Penrose tiling.

The distribution of oscillation frequencies in a Penrose tiling shows bands and gaps whose widths are in proportions expressed by φ.

Related tilings and topics

A variant of the Penrose tiling which is not a quasicrystal

The three variants (P1–P3) of the Penrose tiling are equivalent in the sense of being mutually locally derivable, but there also exist related inequivalent tilings, such as the hexagon-boat-star and Mikulla–Roth tilings. For instance if the matching rules for the rhombus tiling are reduced to a specific restriction on the angles permitted at each vertex, a binary tiling is obtained. Its underlying symmetry is also fivefold but it is not a quasicrystal. It can be obtained either by decorating the rhombuses of the original tiling with smaller ones, or by substitution rules, but not by de Bruijn's cut-and-project method.

The aesthetic value of tilings has long been appreciated and remains a source of interest in them; here the visual appearance (rather than the formal defining properties) of Penrose tilings has attracted attention. The similarity with some decorative patterns used in the Middle East has been noted and Lu and Steinhardt have presented evidence that a Penrose tiling underlies some examples of medieval Islamic art.

Drop City artist Clark Richert used Penrose rhombuses in artwork in 1970. Art historian Martin Kemp has observed that Albrecht Dürer has sketched similar motifs of a rhombus tiling. The Penrose tilling pattern could be used to generate importance sampling samplers with blue noise properties at a high performance.

See also

• Zellige
• Aperiodic tiling
• Girih tiles
• Pinwheel tiling
• Quaquaversal tiling

References

• Austin, David (2005a), "Penrose Tiles Talk Across Miles", Feature Column, Providence: American Mathematical Society.
• Austin, David (2005b), "Penrose Tilings Tied up in Ribbons", Feature Column, Providence: American Mathematical Society.
• Gardner, Martin (1997), Penrose Tiles to Trapdoor Ciphers, Cambridge University Press, ISBN 978-0883855218. (First published by W. H. Freeman, New York (1989), ISBN 978-0716719861.)
  • Chapter 1 (pp. 1–18) is a reprint of Gardner, Martin (January 1977), "Extraordinary nonperiodic tiling that enriches the theory of tiles", Scientific American, 236: 110–121.
• Grünbaum, Branko; Shephard, G. C. (1987), Tilings and Patterns, New York: W. H. Freeman, ISBN 978-716711933 {{citation}}: Check |isbn= value: length (help).
• Set of tiles for covering a surface, 1976-06-24 {{citation}}: Unknown parameter |country-code= ignored (help); Unknown parameter |inventor-first= ignored (help); Unknown parameter |inventor-last= ignored (help); Unknown parameter |inventorlink= ignored (help); Unknown parameter |issue-date= ignored (help); Unknown parameter |patent-number= ignored (help).

External links

There are many internet resources related to Penrose tilings; the following is a selection.

• John Savard. "Penrose Tilings". quadibloc.com. Retrieved 2009-11-28. {{cite web}}: Unknown parameter |separator= ignored (help)
• Eric Hwang. "Penrose Tiling". intendo.net. Retrieved 2009-11-28. {{cite web}}: Unknown parameter |separator= ignored (help)
• E. Harriss and D. Frettlöh. "Penrose Rhomb". Tilings Encyclopedia. Department of Mathematics, University of Bielefeld. Retrieved 2009-11-28. {{cite web}}: Unknown parameter |separator= ignored (help)
• Kevin Brown. "On de Bruijn Grids and Tilings". mathpages.com. Retrieved 2009-11-28. {{cite web}}: Unknown parameter |separator= ignored (help)
• David Eppstein. "Penrose Tiles". The Geometry Junkyard. www.ics.uci.edu/~eppstein. Retrieved 2009-11-28. {{cite web}}: Unknown parameter |separator= ignored (help) This has a list of additional resources.