B-tree
| B-tree | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Tree (data structure) | |||||||||||||||||||||||
| Invented | 1970[1] | |||||||||||||||||||||||
| Invented by | Rudolf Bayer, Edward M. McCreight | |||||||||||||||||||||||
| ||||||||||||||||||||||||
In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children.[2] Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as databases and file systems.
History
[edit]B-trees were invented by Rudolf Bayer and Edward M. McCreight while working at Boeing Research Labs, for the purpose of efficiently managing index pages for large random-access files. The basic assumption was that indices would be so voluminous that only small chunks of the tree could fit in main memory. Bayer and McCreight's paper Organization and maintenance of large ordered indices[1] was first circulated in July 1970 and later published in Acta Informatica.[3]
Bayer and McCreight never explained what, if anything, the B stands for; Boeing, balanced, between, broad, bushy, and Bayer have been suggested.[4][5][6] McCreight, when asked "I want to know what B in B-Tree stands for," answered[5]:
Everybody does!
So you just have no idea what a lunchtime conversation can turn into. So there we were, Rudy and I, at lunch. We had to give the thing a name.... We were working for Boeing at the time, but we couldn't use the name without talking to the lawyers. So there's a B.
It has to do with Balance. There's another B.
Rudy was the senior author. Rudy (Bayer) was several years older than I am, and had ... many more publications than I did. So there's another B.
And so at the lunch table, we never did resolve whether there was one of those that made more sense than the rest.
What Rudy likes to say is, the more you think about what the B in B-Tree means, the better you understand B-Trees!
Definition
[edit]According to Knuth's definition, a B-tree of order m is a tree which satisfies the following properties:[7]
- Every node has at most m children.
- Every node, except for the root and the leaves, has at least ⌈m/2⌉ children.
- The root node has at least two children unless it is a leaf.
- All leaves appear on the same level.
- A non-leaf node with k children contains k−1 keys.
Each internal node's keys act as separation values which divide its subtrees. For example, if an internal node has 3 child nodes (or subtrees) then it must have 2 keys: a1 and a2. All values in the leftmost subtree will be less than a1, all values in the middle subtree will be between a1 and a2, and all values in the rightmost subtree will be greater than a2.
- Internal nodes
- Internal nodes (also known as inner nodes) are all nodes except for leaf nodes and the root node. They are usually represented as an ordered set of elements and child pointers. Every internal node contains a maximum of U children and a minimum of L children. Thus, the number of elements is always 1 less than the number of child pointers (the number of elements is between L−1 and U−1). U must be either 2L or 2L−1; therefore each internal node is at least half full. The relationship between U and L implies that two half-full nodes can be joined to make a legal node, and one full node can be split into two legal nodes (if there's room to push one element up into the parent). These properties make it possible to delete and insert new values into a B-tree and adjust the tree to preserve the B-tree properties.
- The root node
- The root node's number of children has the same upper limit as internal nodes, but has no lower limit. For example, when there are fewer than L−1 elements in the entire tree, the root will be the only node in the tree with no children at all.
- Leaf nodes
- In Knuth's terminology, the "leaf" nodes are the actual data objects / chunks. The internal nodes that are one level above these leaves are what would be called the "leaves" by other authors: these nodes only store keys (at most m-1, and at least m/2-1 if they are not the root) and pointers (one for each key) to nodes carrying the data objects / chunks.
A B-tree of depth n+1 can hold about U times as many items as a B-tree of depth n, but the cost of search, insert, and delete operations grows with the depth of the tree. As with any balanced tree, the cost grows much more slowly than the number of elements.
Some balanced trees store values only at leaf nodes, and use different kinds of nodes for leaf nodes and internal nodes. B-trees keep values in every node in the tree except leaf nodes.
Differences in terminology
[edit]The literature on B-trees is not uniform in its terminology.[8]
Bayer and McCreight (1972),[3] Comer (1979),[2] and others define the order of B-tree as the minimum number of keys in a non-root node. Folk and Zoellick [9] points out that terminology is ambiguous because the maximum number of keys is not clear. An order 3 B-tree might hold a maximum of 6 keys or a maximum of 7 keys. Knuth (1998) avoids the problem by defining the order to be the maximum number of children (which is one more than the maximum number of keys).[7]
The term leaf is also inconsistent. Bayer and McCreight (1972)[3] considered the leaf level to be the lowest level of keys, but Knuth considered the leaf level to be one level below the lowest keys.[9] There are many possible implementation choices. In some designs, the leaves may hold the entire data record; in other designs, the leaves may only hold pointers to the data record. Those choices are not fundamental to the idea of a B-tree.[10]
For simplicity, most authors assume there are a fixed number of keys that fit in a node. The basic assumption is the key size is fixed and the node size is fixed. In practice, variable length keys may be employed.[11]
Informal description
[edit]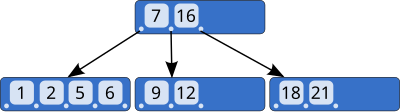
Node structure
[edit]As with other trees, B-trees can be represented as a collection of three types of nodes: root, internal (a.k.a. interior), and leaf.
Note the following variable definitions:
- K: Maximum number of potential search keys for each node in a B-tree. (this value is constant over the entire tree).
- : The pointer to a child node which starts a sub-tree.
- : The pointer to a record which stores the data.
- : The search key at the zero-based node index .
In B-trees, the following properties are maintained for these nodes:
- If exists in any node in a B+ tree, then exists in that node where .
- All leaf nodes have the same number of ancestors (i.e., they are all at the same depth).
Each internal node in a B-tree has the following format:
| pt0 | k0 | pt1 | pr0 | k1 | pt2 | pr1 | ... | kK-1 | ptK | prK-1 |
|---|
| when exists | when and exist | when exists, and does not exist | when and do not exist | when exists | when does not exist |
|---|---|---|---|---|---|
| Points to subtree in which all search keys are less than . | Points to subtree in which all search keys are greater than and are less than . | Points to subtree in which all search keys are greater than . | Here, is empty. | Points to a record with a value equal to . | Here, is empty. |
Each leaf node in a B-tree has the following format:
| pr0 | k0 | pr1 | k1 | ... | prK-1 | kK-1 |
|---|
| when exists | when does not exist |
|---|---|
| Points to a record with a value equal to . | Here, is empty. |
The node bounds are summarized in the table below:
| Node type | Min number of keys |
Max number of keys |
Min number of child nodes |
Max number of child nodes |
|---|---|---|---|---|
| Root node when it is a leaf node | 0 | 0 | 0 | |
| Root node when it is an internal node | 1 | 2[12] | ||
| Internal node | ||||
| Leaf node | 0 | 0 |
Insertion and deletion
[edit]In order to maintain the predefined range of child nodes, internal nodes may be joined or split.
Usually, the number of keys is chosen to vary between and , where is the minimum number of keys, and is the minimum degree or branching factor of the tree. The factor of 2 will guarantee that nodes can be split or combined.
If an internal node has keys, then adding a key to that node can be accomplished by splitting the hypothetical key node into two key nodes and moving the key that would have been in the middle to the parent node. Each split node has the required minimum number of keys. Similarly, if an internal node and its neighbor each have keys, then a key may be deleted from the internal node by combining it with its neighbor. Deleting the key would make the internal node have keys; joining the neighbor would add keys plus one more key brought down from the neighbor's parent. The result is an entirely full node of keys.
A B-tree is kept balanced after insertion by splitting a would-be overfilled node, of keys, into two -key siblings and inserting the mid-value key into the parent. Depth only increases when the root is split, maintaining balance. Similarly, a B-tree is kept balanced after deletion by merging or redistributing keys among siblings to maintain the -key minimum for non-root nodes. A merger reduces the number of keys in the parent potentially forcing it to merge or redistribute keys with its siblings, and so on. The only change in depth occurs when the root has two children, of and (transitionally) keys, in which case the two siblings and parent are merged, reducing the depth by one.
This depth will increase slowly as elements are added to the tree, but an increase in the overall depth is infrequent, and results in all leaf nodes being one more node farther away from the root.
Comparison to other trees
[edit]Because a range of child nodes is permitted, B-trees do not need re-balancing as frequently as other self-balancing search trees, but may waste some space, since nodes are not entirely full.
B-trees have substantial advantages over alternative implementations when the time to access the data of a node greatly exceeds the time spent processing that data, because then the cost of accessing the node may be amortized over multiple operations within the node. This usually occurs when the node data are in secondary storage such as disk drives. By maximizing the number of keys within each internal node, the height of the tree decreases and the number of expensive node accesses is reduced. In addition, rebalancing of the tree occurs less often. The maximum number of child nodes depends on the information that must be stored for each child node and the size of a full disk block or an analogous size in secondary storage. While 2–3 B-trees are easier to explain, practical B-trees using secondary storage need a large number of child nodes to improve performance.
Variants
[edit]The term B-tree may refer to a specific design or it may refer to a general class of designs. In the narrow sense, a B-tree stores keys in its internal nodes but need not store those keys in the records at the leaves. The general class includes variations such as the B+ tree, the B* tree and the B*+ tree.
- In the B+ tree, the internal nodes do not store any pointers to records, thus all pointers to records are stored in the leaf nodes. In addition, a leaf node may include a pointer to the next leaf node to speed up sequential access.[2] Because B+ tree internal nodes have fewer pointers, each node can hold more keys, causing the tree to be shallower and thus faster to search.
- The B* tree balances more neighboring internal nodes to keep the internal nodes more densely packed.[2] This variant ensures non-root nodes are at least 2/3 full instead of 1/2.[13] As the most costly part of operation of inserting the node in B-tree is splitting the node, B*-trees are created to postpone splitting operation as long as they can.[14] To maintain this, instead of immediately splitting up a node when it gets full, its keys are shared with a node next to it. This spill operation is less costly to do than split, because it requires only shifting the keys between existing nodes, not allocating memory for a new one.[14] For inserting, first it is checked whether the node has some free space in it, and if so, the new key is just inserted in the node. However, if the node is full (it has m − 1 keys, where m is the order of the tree as maximum number of pointers to subtrees from one node), it needs to be checked whether the right sibling exists and has some free space. If the right sibling has j < m − 1 keys, then keys are redistributed between the two sibling nodes as evenly as possible. For this purpose, m - 1 keys from the current node, the new key inserted, one key from the parent node and j keys from the sibling node are seen as an ordered array of m + j + 1 keys. The array becomes split by half, so that ⌊(m + j + 1)/2⌋ lowest keys stay in the current node, the next (middle) key is inserted in the parent and the rest go to the right sibling.[14] (The newly inserted key might end up in any of the three places.) The situation when right sibling is full, and left isn't is analogous.[14] When both the sibling nodes are full, then the two nodes (current node and a sibling) are split into three and one more key is shifted up the tree, to the parent node.[14] If the parent is full, then spill/split operation propagates towards the root node.[14] Deleting nodes is somewhat more complex than inserting however.
- The B*+ tree combines the main B+ tree and B* tree features together.[15]
- B-trees can be turned into order statistic trees to allow rapid searches for the Nth record in key order, or counting the number of records between any two records, and various other related operations.[16]
B-tree usage in databases
[edit]This section's tone or style may not reflect the encyclopedic tone used on Wikipedia. (May 2022) |
Time to search a sorted file
[edit]Sorting and searching algorithms can be characterized by the number of comparison operations that must be performed using order notation. A binary search of a sorted table with N records, for example, can be done in roughly ⌈ log2 N ⌉ comparisons. If the table had 1,000,000 records, then a specific record could be located with at most 20 comparisons: ⌈ log2 (1,000,000) ⌉ = 20.
Large databases have historically been kept on disk drives. The time to read a record on a disk drive far exceeds the time needed to compare keys once the record is available due to seek time and a rotational delay. The seek time may be 0 to 20 or more milliseconds, and the rotational delay averages about half the rotation period. For a 7200 RPM drive, the rotation period is 8.33 milliseconds. For a drive such as the Seagate ST3500320NS, the track-to-track seek time is 0.8 milliseconds and the average reading seek time is 8.5 milliseconds.[17] For simplicity, assume reading from disk takes about 10 milliseconds.
The time to locate one record out of a million in the example above would take 20 disk reads times 10 milliseconds per disk read, which is 0.2 seconds.
The search time is reduced because individual records are grouped together in a disk block. A disk block might be 16 kilobytes. If each record is 160 bytes, then 100 records could be stored in each block. The disk read time above was actually for an entire block. Once the disk head is in position, one or more disk blocks can be read with little delay. With 100 records per block, the last 6 or so comparisons don't need to do any disk reads—the comparisons are all within the last disk block read.
To speed up the search further, the time to do the first 13 to 14 comparisons (which each required a disk access) must be reduced.
An index speeds the search
[edit]A B-tree index can be used to improve performance. A B-tree index creates a multi-level tree structure that breaks a database down into fixed-size blocks or pages. Each level of this tree can be used to link those pages via an address location, allowing one page (known as a node, or internal page) to refer to another with leaf pages at the lowest level. One page is typically the starting point of the tree, or the "root". This is where the search for a particular key would begin, traversing a path that terminates in a leaf. Most pages in this structure will be leaf pages which refer to specific table rows.
Because each node (or internal page) can have more than two children, a B-tree index will usually have a shorter height (the distance from the root to the farthest leaf) than a Binary Search Tree. In the example above, initial disk reads narrowed the search range by a factor of two. That can be improved by creating an auxiliary index that contains the first record in each disk block (sometimes called a sparse index). This auxiliary index would be 1% of the size of the original database, but it can be searched quickly. Finding an entry in the auxiliary index would tell us which block to search in the main database; after searching the auxiliary index, we would have to search only that one block of the main database—at a cost of one more disk read.
In the above example the index would hold 10,000 entries and would take at most 14 comparisons to return a result. Like the main database, the last six or so comparisons in the auxiliary index would be on the same disk block. The index could be searched in about eight disk reads, and the desired record could be accessed in 9 disk reads.
Creating an auxiliary index can be repeated to make an auxiliary index to the auxiliary index. That would make an aux-aux index that would need only 100 entries and would fit in one disk block.
Instead of reading 14 disk blocks to find the desired record, we only need to read 3 blocks. This blocking is the core idea behind the creation of the B-tree, where the disk blocks fill-out a hierarchy of levels to make up the index. Reading and searching the first (and only) block of the aux-aux index which is the root of the tree identifies the relevant block in aux-index in the level below. Reading and searching that aux-index block identifies the relevant block to read, until the final level, known as the leaf level, identifies a record in the main database. Instead of 150 milliseconds, we need only 30 milliseconds to get the record.
The auxiliary indices have turned the search problem from a binary search requiring roughly log2 N disk reads to one requiring only logb N disk reads where b is the blocking factor (the number of entries per block: b = 100 entries per block in our example; log100 1,000,000 = 3 reads).
In practice, if the main database is being frequently searched, the aux-aux index and much of the aux index may reside in a disk cache, so they would not incur a disk read. The B-tree remains the standard index implementation in almost all relational databases, and many nonrelational databases use them too.[18]
Insertions and deletions
[edit]If the database does not change, then compiling the index is simple to do, and the index need never be changed. If there are changes, managing the database and its index require additional computation.
Deleting records from a database is relatively easy. The index can stay the same, and the record can just be marked as deleted. The database remains in sorted order. If there are a large number of lazy deletions, then searching and storage become less efficient.[19]
Insertions can be very slow in a sorted sequential file because room for the inserted record must be made. Inserting a record before the first record requires shifting all of the records down one. Such an operation is just too expensive to be practical. One solution is to leave some spaces. Instead of densely packing all the records in a block, the block can have some free space to allow for subsequent insertions. Those spaces would be marked as if they were "deleted" records.
Both insertions and deletions are fast as long as space is available on a block. If an insertion won't fit on the block, then some free space on some nearby block must be found and the auxiliary indices adjusted. The best case is that enough space is available nearby so that the amount of block reorganization can be minimized. Alternatively, some out-of-sequence disk blocks may be used.[18]
Advantages of B-tree usage for databases
[edit]The B-tree uses all of the ideas described above. In particular, a B-tree:
- keeps keys in sorted order for sequential traversing
- uses a hierarchical index to minimize the number of disk reads
- uses partially full blocks to speed up insertions and deletions
- keeps the index balanced with a recursive algorithm
In addition, a B-tree minimizes waste by making sure the interior nodes are at least half full. A B-tree can handle an arbitrary number of insertions and deletions.[18]
Best case and worst case heights
[edit]Let h ≥ –1 be the height of the classic B-tree (see Tree (data structure) § Terminology for the tree height definition). Let n ≥ 0 be the number of entries in the tree. Let m be the maximum number of children a node can have. Each node can have at most m−1 keys.
It can be shown (by induction for example) that a B-tree of height h with all its nodes completely filled has n = mh+1–1 entries. Hence, the best case height (i.e. the minimum height) of a B-tree is:
Let be the minimum number of children an internal (non-root) node must have. For an ordinary B-tree,
Comer (1979) and Cormen et al. (2001) give the worst case height (the maximum height) of a B-tree as[20]
Algorithms
[edit]This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Search
[edit]Searching is similar to searching a binary search tree. Starting at the root, the tree is recursively traversed from top to bottom. At each level, the search reduces its field of view to the child pointer (subtree) whose range includes the search value. A subtree's range is defined by the values, or keys, contained in its parent node. These limiting values are also known as separation values.
Binary search is typically (but not necessarily) used within nodes to find the separation values and child tree of interest.
Insertion
[edit]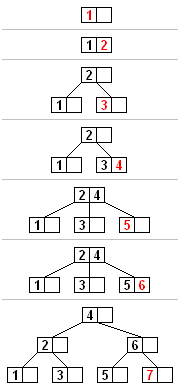
All insertions start at a leaf node. To insert a new element, search the tree to find the leaf node where the new element should be added. Insert the new element into that node with the following steps:
- If the node contains fewer than the maximum allowed number of elements, then there is room for the new element. Insert the new element in the node, keeping the node's elements ordered.
- Otherwise the node is full, evenly split it into two nodes so:
- A single median is chosen from among the leaf's elements and the new element that is being inserted.
- Values less than the median are put in the new left node and values greater than the median are put in the new right node, with the median acting as a separation value.
- The separation value is inserted in the node's parent, which may cause it to be split, and so on. If the node has no parent (i.e., the node was the root), create a new root above this node (increasing the height of the tree).
If the splitting goes all the way up to the root, it creates a new root with a single separator value and two children, which is why the lower bound on the size of internal nodes does not apply to the root. The maximum number of elements per node is U−1. When a node is split, one element moves to the parent, but one element is added. So, it must be possible to divide the maximum number U−1 of elements into two legal nodes. If this number is odd, then U=2L and one of the new nodes contains (U−2)/2 = L−1 elements, and hence is a legal node, and the other contains one more element, and hence it is legal too. If U−1 is even, then U=2L−1, so there are 2L−2 elements in the node. Half of this number is L−1, which is the minimum number of elements allowed per node.
An alternative algorithm supports a single pass down the tree from the root to the node where the insertion will take place, splitting any full nodes encountered on the way pre-emptively. This prevents the need to recall the parent nodes into memory, which may be expensive if the nodes are on secondary storage. However, to use this algorithm, we must be able to send one element to the parent and split the remaining U−2 elements into two legal nodes, without adding a new element. This requires U = 2L rather than U = 2L−1, which accounts for why some[which?] textbooks impose this requirement in defining B-trees.
Deletion
[edit]There are two popular strategies for deletion from a B-tree.
- Locate and delete the item, then restructure the tree to retain its invariants, OR
- Do a single pass down the tree, but before entering (visiting) a node, restructure the tree so that once the key to be deleted is encountered, it can be deleted without triggering the need for any further restructuring
The algorithm below uses the former strategy.
There are two special cases to consider when deleting an element:
- The element in an internal node is a separator for its child nodes
- Deleting an element may put its node under the minimum number of elements and children
The procedures for these cases are in order below.
Deletion from a leaf node
[edit]- Search for the value to delete.
- If the value is in a leaf node, simply delete it from the node.
- If underflow happens, rebalance the tree as described in section "Rebalancing after deletion" below.
Deletion from an internal node
[edit]Each element in an internal node acts as a separation value for two subtrees, therefore we need to find a replacement for separation. Note that the largest element in the left subtree is still less than the separator. Likewise, the smallest element in the right subtree is still greater than the separator. Both of those elements are in leaf nodes, and either one can be the new separator for the two subtrees. Algorithmically described below:
- Choose a new separator (either the largest element in the left subtree or the smallest element in the right subtree), remove it from the leaf node it is in, and replace the element to be deleted with the new separator.
- The previous step deleted an element (the new separator) from a leaf node. If that leaf node is now deficient (has fewer than the required number of nodes), then rebalance the tree starting from the leaf node.
Rebalancing after deletion
[edit]Rebalancing starts from a leaf and proceeds toward the root until the tree is balanced. If deleting an element from a node has brought it under the minimum size, then some elements must be redistributed to bring all nodes up to the minimum. Usually, the redistribution involves moving an element from a sibling node that has more than the minimum number of nodes. That redistribution operation is called a rotation. If no sibling can spare an element, then the deficient node must be merged with a sibling. The merge causes the parent to lose a separator element, so the parent may become deficient and need rebalancing. The merging and rebalancing may continue all the way to the root. Since the minimum element count doesn't apply to the root, making the root be the only deficient node is not a problem. The algorithm to rebalance the tree is as follows:
- If the deficient node's right sibling exists and has more than the minimum number of elements, then rotate left
- Copy the separator from the parent to the end of the deficient node (the separator moves down; the deficient node now has the minimum number of elements)
- Replace the separator in the parent with the first element of the right sibling (right sibling loses one node but still has at least the minimum number of elements)
- The tree is now balanced
- Otherwise, if the deficient node's left sibling exists and has more than the minimum number of elements, then rotate right
- Copy the separator from the parent to the start of the deficient node (the separator moves down; deficient node now has the minimum number of elements)
- Replace the separator in the parent with the last element of the left sibling (left sibling loses one node but still has at least the minimum number of elements)
- The tree is now balanced
- Otherwise, if both immediate siblings have only the minimum number of elements, then merge with a sibling sandwiching their separator taken off from their parent
- Copy the separator to the end of the left node (the left node may be the deficient node or it may be the sibling with the minimum number of elements)
- Move all elements from the right node to the left node (the left node now has the maximum number of elements, and the right node – empty)
- Remove the separator from the parent along with its empty right child (the parent loses an element)
- If the parent is the root and now has no elements, then free it and make the merged node the new root (tree becomes shallower)
- Otherwise, if the parent has fewer than the required number of elements, then rebalance the parent[21]
- Note: The rebalancing operations are different for B+ trees (e.g., rotation is different because parent has copy of the key) and B*-tree (e.g., three siblings are merged into two siblings).
Sequential access
[edit]While freshly loaded databases tend to have good sequential behaviour, this behaviour becomes increasingly difficult to maintain as a database grows, resulting in more random I/O and performance challenges.[22]
Initial construction
[edit]A common special case is adding a large amount of pre-sorted data into an initially empty B-tree. While it is quite possible to simply perform a series of successive inserts, inserting sorted data results in a tree composed almost entirely of half-full nodes. Instead, a special "bulk loading" algorithm can be used to produce a more efficient tree with a higher branching factor.
When the input is sorted, all insertions are at the rightmost edge of the tree, and in particular any time a node is split, we are guaranteed that no more insertions will take place in the left half. When bulk loading, we take advantage of this, and instead of splitting overfull nodes evenly, split them as unevenly as possible: leave the left node completely full and create a right node with zero keys and one child (in violation of the usual B-tree rules).
At the end of bulk loading, the tree is composed almost entirely of completely full nodes; only the rightmost node on each level may be less than full. Because those nodes may also be less than half full, to re-establish the normal B-tree rules, combine such nodes with their (guaranteed full) left siblings and divide the keys to produce two nodes at least half full. The only node which lacks a full left sibling is the root, which is permitted to be less than half full.
In filesystems
[edit]In addition to its use in databases, the B-tree (or § Variants) is also used in filesystems to allow quick random access to an arbitrary block in a particular file. The basic problem is turning the file block address into a disk block address.
Some operating systems require the user to allocate the maximum size of the file when the file is created. The file can then be allocated as contiguous disk blocks. In that case, to convert the file block address into a disk block address, the operating system simply adds the file block address to the address of the first disk block constituting the file. The scheme is simple, but the file cannot exceed its created size.
Other operating systems allow a file to grow. The resulting disk blocks may not be contiguous, so mapping logical blocks to physical blocks is more involved.
MS-DOS, for example, used a simple File Allocation Table (FAT). The FAT has an entry for each disk block,[note 1] and that entry identifies whether its block is used by a file and if so, which block (if any) is the next disk block of the same file. So, the allocation of each file is represented as a linked list in the table. In order to find the disk address of file block , the operating system (or disk utility) must sequentially follow the file's linked list in the FAT. Worse, to find a free disk block, it must sequentially scan the FAT. For MS-DOS, that was not a huge penalty because the disks and files were small and the FAT had few entries and relatively short file chains. In the FAT12 filesystem (used on floppy disks and early hard disks), there were no more than 4,080 [note 2] entries, and the FAT would usually be resident in memory. As disks got bigger, the FAT architecture began to confront penalties. On a large disk using FAT, it may be necessary to perform disk reads to learn the disk location of a file block to be read or written.
TOPS-20 (and possibly TENEX) used a 0 to 2 level tree that has similarities to a B-tree[citation needed]. A disk block was 512 36-bit words. If the file fit in a 512 (29) word block, then the file directory would point to that physical disk block. If the file fit in 218 words, then the directory would point to an aux index; the 512 words of that index would either be NULL (the block isn't allocated) or point to the physical address of the block. If the file fit in 227 words, then the directory would point to a block holding an aux-aux index; each entry would either be NULL or point to an aux index. Consequently, the physical disk block for a 227 word file could be located in two disk reads and read on the third.
Apple's filesystem HFS+ and APFS, Microsoft's NTFS,[23] AIX (jfs2) and some Linux filesystems, such as Bcachefs, Btrfs and ext4, use B-trees.
B*-trees are used in the HFS and Reiser4 file systems.
DragonFly BSD's HAMMER file system uses a modified B+-tree.[24]
Performance
[edit]A B-tree grows slower with growing data amount, than the linearity of a linked list. Compared to a skip list, both structures have the same performance, but the B-tree scales better for growing n. A T-tree, for main memory database systems, is similar but more compact.
Variations
[edit]Access concurrency
[edit]Lehman and Yao[25] showed that all the read locks could be avoided (and thus concurrent access greatly improved) by linking the tree blocks at each level together with a "next" pointer. This results in a tree structure where both insertion and search operations descend from the root to the leaf. Write locks are only required as a tree block is modified. This maximizes access concurrency by multiple users, an important consideration for databases and/or other B-tree-based ISAM storage methods. The cost associated with this improvement is that empty pages cannot be removed from the btree during normal operations. (However, see [26] for various strategies to implement node merging, and source code at.[27])
United States Patent 5283894, granted in 1994, appears to show a way to use a 'Meta Access Method' [28] to allow concurrent B+ tree access and modification without locks. The technique accesses the tree 'upwards' for both searches and updates by means of additional in-memory indexes that point at the blocks in each level in the block cache. No reorganization for deletes is needed and there are no 'next' pointers in each block as in Lehman and Yao.
Parallel algorithms
[edit]Since B-trees are similar in structure to red-black trees, parallel algorithms for red-black trees can be applied to B-trees as well.
Maple tree
[edit]A Maple tree is a B-tree developed for use in the Linux kernel to reduce lock contention in virtual memory management.[29][30][31]
(a,b)-tree
[edit](a,b)-trees are generalizations of B-trees. B-trees require that each internal node have a minimum of children and a maximum of children, for some preset value of . In contrast, an (a,b)-tree allows the minimum number of children for an internal node to be set arbitrarily low. In an (a,b)-tree, each internal node has between a and b children, for some preset values of a and b.
See also
[edit]Notes
[edit]- ^ For FAT, what is called a "disk block" here is what the FAT documentation calls a "cluster", which is a fixed-size group of one or more contiguous whole physical disk sectors. For the purposes of this discussion, a cluster has no significant difference from a physical sector.
- ^ Two of these were reserved for special purposes, so only 4078 could actually represent disk blocks (clusters).
References
[edit]- ^ a b Bayer, R.; McCreight, E. (July 1970). "Organization and maintenance of large ordered indices" (PDF). Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control - SIGFIDET '70. Boeing Scientific Research Laboratories. p. 107. doi:10.1145/1734663.1734671. S2CID 26930249.
- ^ a b c d Comer 1979.
- ^ a b c Bayer & McCreight 1972.
- ^ Comer 1979, p. 123 footnote 1.
- ^ a b Weiner, Peter G. (30 August 2013). "4- Edward M McCreight" – via Vimeo.
- ^ "Stanford Center for Professional Development". scpd.stanford.edu. Archived from the original on 2014-06-04. Retrieved 2011-01-16.
- ^ a b Knuth 1998, p. 483.
- ^ Folk & Zoellick 1992, p. 362.
- ^ a b Folk & Zoellick 1992, p. 363.
- ^ Bayer & McCreight (1972) avoided the issue by saying an index element is a (physically adjacent) pair of (x, a) where x is the key, and a is some associated information. The associated information might be a pointer to a record or records in a random access, but what it was didn't really matter. Bayer & McCreight (1972) states, "For this paper the associated information is of no further interest."
- ^ Folk & Zoellick 1992, p. 379.
- ^ Knuth 1998, p. 488.
- ^ a b c d e f Tomašević, Milo (2008). Algorithms and Data Structures. Belgrade, Serbia: Akademska misao. pp. 274–275. ISBN 978-86-7466-328-8.
- ^ Rigin A. M., Shershakov S. A. (2019-09-10). "SQLite RDBMS Extension for Data Indexing Using B-tree Modifications". Proceedings of the Institute for System Programming of the RAS. 31 (3). Institute for System Programming of the RAS (ISP RAS): 203–216. doi:10.15514/ispras-2019-31(3)-16. S2CID 203144646. Retrieved 2021-08-29.
- ^ "Counted B-Trees". www.chiark.greenend.org.uk. Retrieved 2024-12-27.
- ^ Product Manual: Barracuda ES.2 Serial ATA, Rev. F., publication 100468393 (PDF). Seagate Technology LLC. 2008. p. 6.
- ^ a b c Kleppmann, Martin (2017). Designing Data-Intensive Applications. Sebastopol, California: O'Reilly Media. p. 80. ISBN 978-1-449-37332-0.
- ^ Jan Jannink. "Implementing Deletion in B+-Trees". Section "4 Lazy Deletion".
- ^ Comer 1979, p. 127; Cormen et al. 2001, pp. 439–440
- ^ "Deletion in a B-tree" (PDF). cs.rhodes.edu. Archived (PDF) from the original on 2022-10-09. Retrieved 24 May 2022.
- ^ "Cache Oblivious B-trees". State University of New York (SUNY) at Stony Brook. Retrieved 2011-01-17.
- ^ Mark Russinovich (30 June 2006). "Inside Win2K NTFS, Part 1". Microsoft Developer Network. Archived from the original on 13 April 2008. Retrieved 2008-04-18.
- ^ Matthew Dillon (2008-06-21). "The HAMMER Filesystem" (PDF). Archived (PDF) from the original on 2022-10-09.
- ^ Lehman, Philip L.; Yao, s. Bing (1981). "Efficient locking for concurrent operations on B-trees". ACM Transactions on Database Systems. 6 (4): 650–670. doi:10.1145/319628.319663. S2CID 10756181.
- ^ Wang, Paul (1 February 1991). "An In-Depth Analysis of Concurrent B-tree Algorithms" (PDF). dtic.mil. Archived from the original (PDF) on 4 June 2011. Retrieved 21 October 2022.
- ^ "Downloads - high-concurrency-btree - High Concurrency B-Tree code in C - GitHub Project Hosting". GitHub. Retrieved 2014-01-27.
- ^ "Lockless concurrent B-tree index meta access method for cached nodes".
- ^ "Introducing maple trees [LWN.net]". lwn.net.
- ^ "Maple Tree — The Linux Kernel documentation". docs.kernel.org.
- ^ "Introducing the Maple Tree [LWN.net]". lwn.net.
![]() This article incorporates public domain material from Paul E. Black. "(a,b)-tree". Dictionary of Algorithms and Data Structures. NIST.
This article incorporates public domain material from Paul E. Black. "(a,b)-tree". Dictionary of Algorithms and Data Structures. NIST.
Sources
[edit]- Bayer, R.; McCreight, E. (1972). "Organization and Maintenance of Large Ordered Indexes" (PDF). Acta Informatica. 1 (3): 173–189. doi:10.1007/bf00288683. S2CID 29859053..
- Comer, Douglas (June 1979). "The Ubiquitous B-Tree". Computing Surveys. 11 (2): 123–137. doi:10.1145/356770.356776. ISSN 0360-0300. S2CID 101673..
- Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford (2001). Introduction to Algorithms (Second ed.). MIT Press and McGraw-Hill. pp. 434–454. ISBN 0-262-03293-7. Chapter 18: B-Trees.
- Folk, Michael J.; Zoellick, Bill (1992). File Structures (2nd ed.). Addison-Wesley. ISBN 0-201-55713-4..
- Knuth, Donald (1998). Sorting and Searching. The Art of Computer Programming. Vol. 3 (Second ed.). Addison-Wesley. ISBN 0-201-89685-0. Section 6.2.4: Multiway Trees, pp. 481–491. Also, pp. 476–477 of section 6.2.3 (Balanced Trees) discusses 2–3 trees.
Original papers
[edit]- Bayer, Rudolf; McCreight, E. (July 1970), Organization and Maintenance of Large Ordered Indices, vol. Mathematical and Information Sciences Report No. 20, Boeing Scientific Research Laboratories.
- Bayer, Rudolf (1971). "Binary B-Trees for Virtual Memory". Proceedings of 1971 ACM-SIGFIDET Workshop on Data Description, Access and Control. San Diego, California..
External links
[edit]- B-tree lecture by David Scot Taylor, SJSU
- B-Tree visualisation (click "init")
- Animated B-Tree visualization
- B-tree and UB-tree on Scholarpedia Curator: Dr Rudolf Bayer
- B-Trees: Balanced Tree Data Structures Archived 2010-03-05 at the Wayback Machine
- NIST's Dictionary of Algorithms and Data Structures: B-tree
- B-Tree Tutorial
- The InfinityDB BTree implementation
- Cache Oblivious B(+)-trees
- Dictionary of Algorithms and Data Structures entry for B*-tree
- Open Data Structures - Section 14.2 - B-Trees, Pat Morin
- Counted B-Trees
- B-Tree .Net, a modern, virtualized RAM & Disk implementation
Bulk loading
- Shetty, Soumya B. (2010). A user configurable implementation of B-trees (Thesis). Iowa State University.
- Kaldırım, Semih (28 April 2015). "File Organization, ISAM, B+ Tree and Bulk Loading" (PDF). Ankara, Turkey: Bilkent University. pp. 4–6. Archived (PDF) from the original on 2022-10-09.
- "ECS 165B: Database System Implementation: Lecture 6" (PDF). University of California, Davis. 9 April 2010. p. 23. Archived (PDF) from the original on 2022-10-09.
- "BULK INSERT (Transact-SQL) in SQL Server 2017". Microsoft Docs. 6 September 2018.
























