Central binomial coefficient

In mathematics the nth central binomial coefficient is defined in terms of the binomial coefficient by

${2n \choose n} = \frac{(2n)!}{(n!)^2}\text{ for all }n \geq 0.$

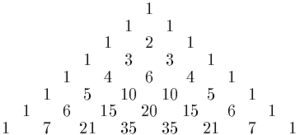
They are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle. The first few central binomial coefficients starting at n = 0 are:

1, 2, 6, 20, 70, 252, 924, 3432, 12870, 48620, … (sequence A000984 in OEIS)

Properties

These numbers have the generating function

$\frac{1}{\sqrt{1-4x}} = 1 + 2x + 6x^2 + 20x^3 + 70x^4 + 252x^5 + \cdots.$

By Stirling's formula we have

${2n \choose n} \sim \frac{4^n}{\sqrt{\pi n}}\text{ as }n\rightarrow\infty.$

Some useful bounds are

$\frac{4^n}{\sqrt{4n}} \leq {2n \choose n} \leq \frac{4^n}{\sqrt{3n+1}}\text{ for all }n \geq 1$

and, if more accuracy is required,

${2n \choose n} = \frac{4^n}{\sqrt{\pi n}}\left(1-\frac{c_n}{n}\right)\text{ where }\frac{1}{9} < c_n < \frac{1}{8}$ for all $n \geq 1.$

The closely related Catalan numbers C_n are given by:

$C_n = \frac{1}{n+1} {2n \choose n} = {2n \choose n} - {2n \choose n+1}\text{ for all }n \geq 0.$

A slight generalization of central binomial coefficients is to take them as ${ m \choose {\lfloor \frac{m}{2} \rfloor} }$ and so the former definition is a particular case when m = 2n, that is, when m is even.

See also

• Erdős squarefree conjecture
• Central multinomial coefficients

External links

• Central binomial coefficient on PlanetMath
• Binomial coefficient on PlanetMath
• Pascal's triangle on PlanetMath
• Catalan numbers on PlanetMath

This article incorporates material from Central binomial coefficient on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.