Circle packing in a square
Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack n unit circles into the smallest possible square. Equivalently, the problem is to arrange n points in a unit square aiming to get the greatest minimal separation, dn, between points.[1] To convert between these two formulations of the problem, the square side for unit circles will be L = 2 + 2/dn.
Solutions
[edit]Solutions (not necessarily optimal) have been computed for every N ≤ 10,000.[2] Solutions up to N = 20 are shown below.[2] The obvious square packing is optimal for 1, 4, 9, 16, 25, and 36 circles (the six smallest square numbers), but ceases to be optimal for larger squares from 49 onwards.[2]
| Number of circles (n) | Square side length (L) | dn[1] | Number density (n/L2) | Figure |
|---|---|---|---|---|
| 1 | 2 | ∞ | 0.25 | |
| 2 | ≈ 3.414... |
≈ 1.414... |
0.172... | 
|
| 3 | ≈ 3.931... |
≈ 1.035... |
0.194... | 
|
| 4 | 4 | 1 | 0.25 | 
|
| 5 | ≈ 4.828... |
≈ 0.707... |
0.215... | 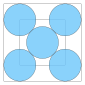
|
| 6 | ≈ 5.328... |
≈ 0.601... |
0.211... | 
|
| 7 | ≈ 5.732... |
≈ 0.536... |
0.213... | 
|
| 8 | ≈ 5.863... |
≈ 0.518... |
0.233... | 
|
| 9 | 6 | 0.5 | 0.25 | 
|
| 10 | 6.747... | 0.421... OEIS: A281065 | 0.220... | 
|
| 11 | ≈ 7.022... |
0.398... | 0.223... | 
|
| 12 | ≈ 7.144... |
≈ 0.389... |
0.235... | 
|
| 13 | 7.463... | 0.366... | 0.233... | 
|
| 14 | ≈ 7.732... |
≈ 0.349... |
0.226... | 
|
| 15 | ≈ 7.863... |
≈ 0.341... |
0.243... | 
|
| 16 | 8 | 0.333... | 0.25 | 
|
| 17 | 8.532... | 0.306... | 0.234... | 
|
| 18 | ≈ 8.656... |
≈ 0.300... |
0.240... | 
|
| 19 | 8.907... | 0.290... | 0.240... | 
|
| 20 | ≈ 8.978... |
≈ 0.287... |
0.248... | 
|
Circle packing in a rectangle
[edit]Dense packings of circles in non-square rectangles have also been the subject of investigations.[3][4]
See also
[edit]References
[edit]- ^ a b Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). Unsolved Problems in Geometry. New York: Springer-Verlag. pp. 108–110. ISBN 0-387-97506-3.
- ^ a b c Eckard Specht (20 May 2010). "The best known packings of equal circles in a square". Retrieved 25 May 2010.
- ^ Lubachevsky, Boris D.; Graham, Ronald L. (2009). "Minimum perimeter rectangles that enclose congruent non-overlapping circles". Discrete Mathematics. 309 (8). Elsevier BV: 1947–1962. arXiv:math/0412443. doi:10.1016/j.disc.2008.03.017. ISSN 0012-365X. S2CID 783236.
- ^ Specht, E. (2013). "High density packings of equal circles in rectangles with variable aspect ratio". Computers & Operations Research. 40 (1). Elsevier BV: 58–69. doi:10.1016/j.cor.2012.05.011. ISSN 0305-0548.























