Dagger compact category
In category theory, a branch of mathematics, dagger compact categories (or dagger compact closed categories) first appeared in 1989 in the work of Sergio Doplicher and John E. Roberts on the reconstruction of compact topological groups from their category of finite-dimensional continuous unitary representations (that is, Tannakian categories).[1] They also appeared in the work of John Baez and James Dolan as an instance of semistrict k-tuply monoidal n-categories, which describe general topological quantum field theories,[2] for n = 1 and k = 3. They are a fundamental structure in Samson Abramsky and Bob Coecke's categorical quantum mechanics.[3][4][5]
Overview[edit]
Dagger compact categories can be used to express and verify some fundamental quantum information protocols, namely: teleportation, logic gate teleportation and entanglement swapping, and standard notions such as unitarity, inner-product, trace, Choi–Jamiolkowsky duality, complete positivity, Bell states and many other notions are captured by the language of dagger compact categories.[3] All this follows from the completeness theorem, below. Categorical quantum mechanics takes dagger compact categories as a background structure relative to which other quantum mechanical notions like quantum observables and complementarity thereof can be abstractly defined. This forms the basis for a high-level approach to quantum information processing.
Formal definition[edit]
A dagger compact category is a dagger symmetric monoidal category which is also compact closed, together with a relation to tie together the dagger structure to the compact structure. Specifically, the dagger is used to connect the unit to the counit, so that, for all in , the following diagram commutes:
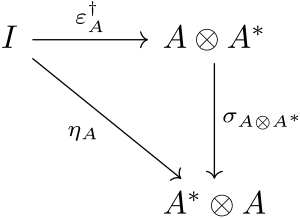
To summarize all of these points:
- A category is closed if it has an internal hom functor; that is, if the hom-set of morphisms between two objects of the category is an object of the category itself (rather than of Set).
- A category is monoidal if it is equipped with an associative bifunctor that is associative, natural and has left and right identities obeying certain coherence conditions.
- A monoidal category is symmetric monoidal, if, for every pair A, B of objects in C, there is an isomorphism that is natural in both A and B, and, again, obeys certain coherence conditions (see symmetric monoidal category for details).
- A monoidal category is compact closed, if every object has a dual object . Categories with dual objects are equipped with two morphisms, the unit and the counit , which satisfy certain coherence or yanking conditions.
- A category is a dagger category if it is equipped with an involutive functor that is the identity on objects, but maps morphisms to their adjoints.
- A monoidal category is dagger symmetric if it is a dagger category and is symmetric, and has coherence conditions that make the various functors natural.
A dagger compact category is then a category that is each of the above, and, in addition, has a condition to relate the dagger structure to the compact structure. This is done by relating the unit to the counit via the dagger:
shown in the commuting diagram above. In the category FdHilb of finite-dimensional Hilbert spaces, this last condition can be understood as defining the dagger (the Hermitian conjugate) as the transpose of the complex conjugate.
Examples[edit]
The following categories are dagger compact.
- The category FdHilb of finite dimensional Hilbert spaces and linear maps. The morphisms are linear operators between Hilbert spaces. The product is the usual tensor product, and the dagger here is the Hermitian conjugate.
- The category Rel of Sets and relations. The product is, of course, the Cartesian product. The dagger here is just the opposite.
- The category of finitely generated projective modules over a commutative ring. The dagger here is just the matrix transpose.
- The category nCob of cobordisms. Here, the n-dimensional cobordisms are the morphisms, the disjoint union is the tensor, and the reversal of the objects (closed manifolds) is the dagger. A topological quantum field theory can be defined as a functor from nCob into FdHilb.[6]
- The category Span(C) of spans for any category C with finite limits.
Infinite-dimensional Hilbert spaces are not dagger compact, and are described by dagger symmetric monoidal categories.
Structural theorems[edit]
Selinger showed that dagger compact categories admit a Joyal-Street style diagrammatic language[7] and proved that dagger compact categories are complete with respect to finite dimensional Hilbert spaces[8][9] i.e. an equational statement in the language of dagger compact categories holds if and only if it can be derived in the concrete category of finite dimensional Hilbert spaces and linear maps. There is no analogous completeness for Rel or nCob.
This completeness result implies that various theorems from Hilbert spaces extend to this category. For example, the no-cloning theorem implies that there is no universal cloning morphism.[10] Completeness also implies far more mundane features as well: dagger compact categories can be given a basis in the same way that a Hilbert space can have a basis. Operators can be decomposed in the basis; operators can have eigenvectors, etc.. This is reviewed in the next section.
Basis[edit]
The completeness theorem implies that basic notions from Hilbert spaces carry over to any dagger compact category. The typical language employed, however, changes. The notion of a basis is given in terms of a coalgebra. Given an object A from a dagger compact category, a basis is a comonoid object . The two operations are a copying or comultiplication δ: A → A ⊗ A morphism that is cocommutative and coassociative, and a deleting operation or counit morphism ε: A → I . Together, these obey five axioms:[11]
Comultiplicativity:
Coassociativity:
Cocommutativity:
Isometry:
To see that these relations define a basis of a vector space in the traditional sense, write the comultiplication and counit using bra–ket notation, and understanding that these are now linear operators acting on vectors in a Hilbert space H:
and
The only vectors that can satisfy the above five axioms must be orthogonal to one-another; the counit then uniquely specifies the basis. The suggestive names copying and deleting for the comultiplication and counit operators come from the idea that the no-cloning theorem and no-deleting theorem state that the only vectors that it is possible to copy or delete are orthogonal basis vectors.
General results[edit]
Given the above definition of a basis, a number of results for Hilbert spaces can be stated for compact dagger categories. We list some of these below, taken from[11] unless otherwise noted.
- A basis can also be understood to correspond to an observable, in that a given observable factors on (orthogonal) basis vectors. That is, an observable is represented by an object A together with the two morphisms that define a basis: .
- An eigenstate of the observable is any object for which
- Eigenstates are orthogonal to one another.[clarification needed]
- An object is complementary to the observable if[clarification needed]
- (In quantum mechanics, a state vector is said to be complementary to an observable if any measurement result is equiprobable. viz. an spin eigenstate of Sx is equiprobable when measured in the basis Sz, or momentum eigenstates are equiprobable when measured in the position basis.)
- Two observables and are complementary if
- Complementary objects generate unitary transformations. That is,
- is unitary if and only if is complementary to the observable
References[edit]
- ^ Doplicher, S.; Roberts, J. (1989). "A new duality theory for compact groups". Invent. Math. 98: 157–218. Bibcode:1989InMat..98..157D. doi:10.1007/BF01388849. S2CID 120280418.
- ^ Baez, J.C.; Dolan, J. (1995). "Higher-dimensional Algebra and Topological Quantum Field Theory". J. Math. Phys. 36 (11): 6073–6105. arXiv:q-alg/9503002. Bibcode:1995JMP....36.6073B. CiteSeerX 10.1.1.269.4681. doi:10.1063/1.531236. S2CID 14908618.
- ^ a b Abramsky, S.; Coecke, B. (2004). "A categorical semantics of quantum protocols". Proceedings of the 19th IEEE conference on Logic in Computer Science (LiCS'04). IEEE. pp. 415–425. arXiv:quant-ph/0402130. CiteSeerX 10.1.1.330.7289. doi:10.1109/LICS.2004.1319636. ISBN 0-7695-2192-4. S2CID 1980118.
- ^ Abramsky, S.; Coecke, B. (2009). "Categorical quantum mechanics". In Engesser, K.; Gabbay, D.M.; Lehmann, D. (eds.). Handbook of Quantum Logic and Quantum Structures. Elsevier. pp. 261–323. arXiv:0808.1023. ISBN 978-0-08-093166-1.
- ^ Abramsky and Coecke used the term strongly compact closed categories, since a dagger compact category is a compact closed category augmented with a covariant involutive monoidal endofunctor.
- ^ Atiyah, M. (1989). "Topological quantum field theories" (PDF). Inst. Hautes Études Sci. Publ. Math. 68: 175–186. doi:10.1007/BF02698547. S2CID 121647908.
- ^ Selinger, Peter (2007). "Dagger compact closed categories and completely positive maps: (Extended Abstract)". Electronic Notes in Theoretical Computer Science. 170 (Proceedings of the 3rd International Workshop on Quantum Programming Languages (QPL 2005)): 139–163. CiteSeerX 10.1.1.84.8476. doi:10.1016/j.entcs.2006.12.018.
- ^ Selinger, P. (2011). "Finite dimensional Hilbert spaces are complete for dagger compact closed categories". Electronic Notes in Theoretical Computer Science. 270 (Proceedings of the Joint 5th International Workshop on Quantum Physics and Logic and 4th Workshop on Developments in Computational Models (QPL/DCM 2008)): 113–9. arXiv:1207.6972. CiteSeerX 10.1.1.749.4436. doi:10.1016/j.entcs.2011.01.010.
- ^ Hasegawa, M.; Hofmann, M.; Plotkin, G. (2008). "Finite Dimensional Vector Spaces Are Complete for Traced Symmetric Monoidal Categories". In Avron, A.; Dershowitz, N.; Rabinovich, A. (eds.). Pillars of Computer Science. Lecture Notes in Computer Science. Vol. 4800. Springer. pp. 367–385. CiteSeerX 10.1.1.443.3495. doi:10.1007/978-3-540-78127-1_20. ISBN 978-3-540-78127-1. S2CID 15045491.
- ^ Abramsky, S. (2010). "No-Cloning in categorical quantum mechanics". In Mackie, I.; Gay, S. (eds.). Semantic Techniques for Quantum Computation. Cambridge University Press. pp. 1–28. ISBN 978-0-521-51374-6.
- ^ a b Coecke, Bob (2009). "Quantum Picturalism". Contemporary Physics. 51: 59–83. arXiv:0908.1787. doi:10.1080/00107510903257624. S2CID 752173.
- Dagger-compact category at the nLab


























