Efficient frontier
In modern portfolio theory, the efficient frontier (or portfolio frontier) is an investment portfolio which occupies the "efficient" parts of the risk–return spectrum. Formally, it is the set of portfolios which satisfy the condition that no other portfolio exists with a higher expected return but with the same standard deviation of return (i.e., the risk).[1] The efficient frontier was first formulated by Harry Markowitz in 1952;[2] see Markowitz model.
Overview[edit]

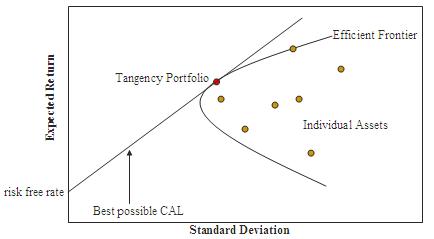
A combination of assets, i.e. a portfolio, is referred to as "efficient" if it has the best possible expected level of return for its level of risk (which is represented by the standard deviation of the portfolio's return).[3] Here, every possible combination of risky assets can be plotted in risk–expected return space, and the collection of all such possible portfolios defines a region in this space. In the absence of the opportunity to hold a risk-free asset, this region is the opportunity set (the feasible set). The positively sloped (upward-sloped) top boundary of this region is a portion of a hyperbola[4] and is called the "efficient frontier".
If a risk-free asset is also available, the opportunity set is larger, and its upper boundary, the efficient frontier, is a straight line segment emanating from the vertical axis at the value of the risk-free asset's return and tangent to the risky-assets-only opportunity set. All portfolios between the risk-free asset and the tangency portfolio are portfolios composed of risk-free assets and the tangency portfolio, while all portfolios on the linear frontier above and to the right of the tangency portfolio are generated by borrowing at the risk-free rate and investing the proceeds into the tangency portfolio.
Among certain universes of assets, academics have found that the efficient frontier (the Markowitz model, more broadly) has been susceptible to issues such as model instability where, for example, the reference assets have a high degree of correlation.[5]
See also[edit]
- Markowitz model
- Modern portfolio theory
- Critical line method, an optimization algorithm developed by Markowitz for this problem
References[edit]
- ^ "Markowitz efficient frontier". NASDAQ. nasdaq.com. Retrieved 15 May 2017.
- ^ Markowitz, H.M. (March 1952). "Portfolio Selection". The Journal of Finance. 7 (1): 77–91. doi:10.2307/2975974. JSTOR 2975974.
- ^ Edwin J. Elton and Martin J. Gruber (2011). Investments and Portfolio Performance. World Scientific. pp. 382–383. ISBN 978-981-4335-39-3.
- ^ Merton, Robert. "An analytic derivation of the efficient portfolio frontier," Journal of Financial and Quantitative Analysis 7, September 1972, 1851-1872.
- ^ Henide, Karim (2023). "Sherman ratio optimization: constructing alternative ultrashort sovereign bond portfolios". Journal of Investment Strategies. doi:10.21314/JOIS.2023.001.

