Five-room puzzle
This classical,[1] popular puzzle involves a large rectangle divided into five "rooms". The objective of the puzzle is to cross each "wall" of the diagram with a continuous line only once.[2]
Solutions

Bottom: A solution on a torus — the dotted line is on the back side of the torus (animation)
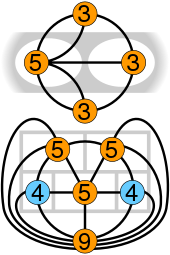
As with the Seven Bridges of Königsberg, the puzzle may be represented in graphical form with each room corresponding to a vertex (including the outside area as a room) and two vertices joined by an edge if the rooms have a common wall. Because there is more than one pair of vertices with an odd number of edges, the resulting multigraph does not contain an Eulerian path nor an Eulerian circuit, which means that this puzzle cannot be solved.
By bending the rules, a related puzzle could be solved. For instance, by permitting passage through more than one wall at a time (that is, through a corner of a room), or by solving the puzzle on a torus (doughnut) instead of a flat plane.
Informal proof of impossibility
Even without using graph theory, it is not difficult to show that the Five Room Puzzle has no solution. First, the rules must be clarified. The rooms and the solution line must all be drawn on a single side of a normal flat sheet of paper. The solution line must be continuous, but can bend sharply or smoothly in any way and can even cross over itself (but not at a wall, so this is often prohibited). The solution line must cross over each "wall" exactly once, where "cross over" means to pass completely from one to the other of the two rooms that are separated by the "wall", or from a room to the area outside the drawing. This precludes "crossing" two walls at the same time by drawing the solution line through the corner at which they meet. It also precludes "crossing" a wall by drawing the solution line up to a wall, perhaps along it, but then leaving the wall on the same side. There are 16 "walls", seven separating rooms and nine separating the rooms from the area outside the drawing.
The method of proof is proof by contradiction. That is, we proceed as if a solution exists and discover some properties of all solutions. These put us in an impossible situation and thus we have to conclude that we were wrong - there is no solution after all.[3]
Imagine that there is an "observer" in each "room". The observer can see the solution line when it is in his room, but not otherwise. As the solution line is drawn, he will see it enter his room through one wall and leave through another. He may also see that the line starts in his room and/or ends in his room. There is no observer in the area outside the drawing, so there are five observers.
Consider, first, the observers in the lower-left and lower-right rooms. Each of these rooms has four walls. If the solution line starts in one of these rooms, its observer will see the line leave through a wall. Then it will come back into the room through another wall and leave again through a third. Finally, it will come back into the room through the fourth wall and end. If the solution line starts somewhere else, the observer will see the solution line come into and leave his room exactly twice, passing through all four walls in some order. There is no problem with any of this.
Consider, however, the observers in the remaining three rooms. Each of these rooms has five walls. If the solution line starts in one of these rooms, its observer will see the line leave (through one wall), re-enter and leave again (two more walls) and enter and leave a second time (the last two walls). If the solution line starts somewhere else, the observer will see the solution line enter and leave (two walls), enter and leave a second time (two more walls) and finally enter through the fifth wall and end (all five walls have been crossed, so the line cannot get back out of the room again). So, we see that for the rooms with five walls, the solution line must either start inside the room or it must end inside the room. There is no other possibility. In our arguments, we have said nothing about exactly which walls the solution line crosses, the order in which it crosses them or where the line goes when it is outside a particular room. Therefore, these arguments apply to all solutions that obey the rules. Again, for the rooms with five walls, the solution line must either start or end inside the room.
But, we have three rooms with five walls. The solution line has one start and one end, so it can pass through all five walls of two of these rooms. However, having run out of ends, the line can not pass through all of the walls of the third five-walled room. Therefore, the solution line cannot be drawn to obey the rules.
Notes
- ^ Gardner 1959, p. 112 Gardner titles the problem (puzzle) as "Cross the Network" and refers to it as one of the oldest of topological puzzles.
- ^ According to Norris 1985, p.207 "One often encounters Eulerian graphs as puzzles. Consider the famous floor plan that consists of five rooms interconnected with themselves and the outside by doors on every wall. The puzzle is to start in one room or the outside, walk through every doorway exactly once, and return to the starting point."
- ^ This argument is an expansion of one outlined by Jacobs (1970, pp. 489-491).
References
- Gardner, Martin (1959), The Scientific American book of Mathematical Puzzles and Diversions, New York: Simon and Schuster
- Jacobs, Harold R. (1970), Mathematics / A Human Endeavor, W.H. Freeman, ISBN 0-7167-0439-0
- Norris, Fletcher R. (1985), Discrete structures: an introduction to mathematics for computer science, Prentice-Hall, ISBN 9780132152600
External links
- History and solution to the 5 Room House puzzle by Archimedes Laboratory


