Fundamental frequency

Vibration and standing waves in a string, The fundamental and the first 6 overtones

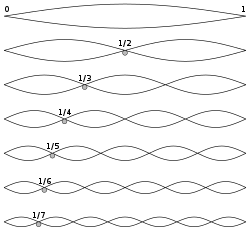
The fundamental frequency, often referred to simply as the fundamental, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids (e.g. Fourier series), the fundamental frequency is the lowest frequency sinusoidal in the sum. In some contexts, the fundamental is usually abbreviated as f₀ (or FF), indicating the lowest frequency counting from zero. In other contexts, it is more common to abbreviate it as f₁, the first harmonic. (The second harmonic is then f₂ = 2⋅f₁, etc. In this context, the zeroth harmonic would be 0 Hz.)

All sinusoidal and many non-sinusoidal waveforms are periodic, which is to say they repeat exactly over time. A single period is thus the smallest repeating unit of a signal, and one period describes the signal completely. We can show a waveform is periodic by finding some period T for which the following equation is true:

$x(t) = x(t + n \cdot T)\text{ for all }n \in \mathbb{N}$

Where x(t) is the function of the waveform.

This means that for multiples of some period T the value of the signal is always the same. The least possible value of T for which this is true is called the fundamental period and the fundamental frequency (f₀) is:

$f_0 = \frac{1}{T}$^{[citation needed]}

Where f₀ is the fundamental frequency and T is the fundamental period.

The fundamental frequency of a sound wave in a tube with a single CLOSED end can be found using the following equation:

$f_0 = \frac{v}{4L}$

L can be found using the following equation:

$L = \frac{\lambda}{4}$

λ (lambda) can be found using the following equation:

$\lambda = \frac{v}{f_0}$

The fundamental frequency of a sound wave in a tube with either BOTH ends OPEN or CLOSED can be found using the following equation:

$f_0 = \frac{v}{2L}$

L can be found using the following equation:

$L = \frac{\lambda}{2}$

The wavelength, which is the distance in the medium between the beginning and end of a cycle, is found using the following equation:

$\lambda = \frac{v}{f_0}$

Where:

f₀ = fundamental frequency

L = length of the tube

v = wave velocity of the sound wave

λ = wavelength

At 20 °C (68 °F) the speed of sound in air is 343 m/s (1129 ft/s). This speed is temperature dependent and does increase at a rate of 0.6 m/s for each degree Celsius increase in temperature (1.1 ft/s for every increase of 1 °F).

The velocity of a sound wave at different temperatures:-

• v = 343.2 m/s at 20 °C
• v = 331.3 m/s at 0 °C

Mechanical systems

Consider a beam, fixed at one end and having a mass attached to the other; this would be a single degree of freedom (SDoF) oscillator. Once set into motion it will oscillate at its natural frequency. For a single degree of freedom oscillator, a system in which the motion can be described by a single coordinate, the natural frequency depends on two system properties: mass and stiffness; (providing the system is undamped). The radian frequency, ω_n, can be found using the following equation:

$\omega_\mathrm{n}^2 = \frac{k}{m} \,$

Where:
k = stiffness of the beam
m = mass of weight
ω_n = radian frequency (radians per second)

From the radian frequency, the natural frequency, f_n, can be found by simply dividing ω_n by 2π. Without first finding the radian frequency, the natural frequency can be found directly using:

$f_\mathrm{n} = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \,$

Where:
f_n = natural frequency in hertz (cycles/second)
k = stiffness of the beam (Newtons/meter or N/m)
m = mass at the end (kg)
while doing the modal analysis of structures and mechanical equipment, the frequency of 1st mode is called fundamental frequency.

See also

• Missing fundamental
• Natural frequency
• Oscillation
• Hertz
• Electronic tuner
• Scale of harmonics
• Pitch detection algorithm