Great-circle distance

The great-circle or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere (as opposed to going through the sphere's interior). Because spherical geometry is different from ordinary Euclidean geometry, the equations for distance take on a different form. The distance between two points in Euclidean space is the length of a straight line from one point to the other. On the sphere, however, there are no straight lines. In non-Euclidean geometry, straight lines are replaced with geodesics. Geodesics on the sphere are the great circles (circles on the sphere whose centers are coincident with the center of the sphere).

Through any two points on a sphere which are not directly opposite each other, there is a unique great circle. The two points separate the great circle into two arcs. The length of the shorter arc is the great-circle distance between the points. A great circle endowed with such a distance is the Riemannian circle.

Between two points which are directly opposite each other, called antipodal points, there are infinitely many great circles, but all great circle arcs between antipodal points have the same length, i.e. half the circumference of the circle, or $\pi r$, where r is the radius of the sphere.

Because the Earth is nearly spherical (see Earth radius) equations for great-circle distance can be used to roughly calculate the shortest distance between points on the surface of the Earth (as the crow flies), and so have applications in navigation.

Formulas

Let $\phi_s,\lambda_s;\ \phi_f,\lambda_f\;\!$ be the geographical latitude and longitude of two points (a base "standpoint" and the destination "forepoint"), respectively, and $\Delta\phi,\Delta\lambda\;\!$ their absolute differences; then $\Delta\widehat{\sigma}\;\!$, the central angle between them, is given by the spherical law of cosines:

${\color{white}\Big|}\Delta\widehat{\sigma}=\arccos\big(\sin\phi_s\sin\phi_f+\cos\phi_s\cos\phi_f\cos\Delta\lambda\big).\;\!$

The distance d, i.e. the arc length, for a sphere of radius r and $\Delta \widehat{\sigma}\!$ given in

$d = r \, \Delta\widehat{\sigma}.\,\!$

This arccosine formula above can have large rounding errors if the distance is small (if the two points are a kilometer apart the cosine of the central angle comes out 0.99999999). An equation known as the haversine formula is numerically better-conditioned for small distances:

${\color{white}\frac{\bigg|}{|}}\Delta\widehat{\sigma} =2\arcsin\left(\sqrt{\sin^2\left(\frac{\Delta\phi}{2}\right)+\cos{\phi_s}\cos{\phi_f}\sin^2\left(\frac{\Delta\lambda}{2}\right)}\right).\;\!$

Historically, the use of this formula was simplified by the availability of tables for the haversine function: hav(θ) = sin² (θ/2).

Although this formula is accurate for most distances on a sphere, it too suffers from rounding errors for the special (and somewhat unusual) case of antipodal points (on opposite ends of the sphere). A more complicated formula that is accurate for all distances is the following special case (a sphere, which is an ellipsoid with equal major and minor axes) of the Vincenty formula (which more generally is a method to compute distances on ellipsoids):

${\color{white}\frac{\bigg|}{|}|}\Delta\widehat{\sigma}=\arctan\left(\frac{\sqrt{\left(\cos\phi_f\sin\Delta\lambda\right)^2+\left(\cos\phi_s\sin\phi_f-\sin\phi_s\cos\phi_f\cos\Delta\lambda\right)^2}}{\sin\phi_s\sin\phi_f+\cos\phi_s\cos\phi_f\cos\Delta\lambda}\right).\;\!$

When programming a computer, one should use the atan2() function rather than the ordinary arctangent function (atan()), in order to simplify handling of the case where the denominator is zero, and to compute $\Delta\widehat{\sigma}\;\!$ unambiguously in all quadrants. Also, make sure that all latitudes and longitudes are in radians (rather than degrees) if that is what your programming language's sin(), cos() and atan2() functions expect (1 radian = 180 / π degrees, 1 degree = π / 180 radians).

Vector version

Another representation of similar formulas, but using n-vector instead of latitude/longitude to describe the positions, is found by means of 3D vector algebra, i.e. utilizing the dot product, cross product, or a combination:

$\begin{align} & \Delta \hat{\sigma }=\text{arccos}\left( \boldsymbol{n}_{es}^{e}\cdot \boldsymbol{n}_{ef}^{e} \right) \\ & \Delta \hat{\sigma }=\text{arcsin}\left( \left| \boldsymbol{n}_{es}^{e}\times \boldsymbol{n}_{ef}^{e} \right| \right) \\ & \Delta \hat{\sigma }=\text{arctan}\left( \frac{\left| \boldsymbol{n}_{es}^{e}\times \boldsymbol{n}_{ef}^{e} \right|}{\boldsymbol{n}_{es}^{e}\cdot \boldsymbol{n}_{ef}^{e}} \right) \\ \end{align}\,\!$

where $\boldsymbol{n}_{es}^{e}\,\!$ and $\boldsymbol{n}_{ef}^{e}\,\!$ are the n-vectors representing the two positions s and f. Similarly to the equations above based on latitude and longitude, the expression based on arctan is the only one that is well-conditioned for all angles. If the two positions are originally given as latitudes and longitudes, a conversion to n-vectors must first be performed.

From chord length

A line through three-dimensional space between points of interest on a spherical Earth is the chord of the great circle between the points. The central angle between the two points can be determined from the chord length. The great circle distance is proportional to the central angle.

The great circle chord length, $C_h\,\!$, may be calculated as follows for the corresponding unit sphere, by means of Cartesian subtraction:

$\begin{align} &\Delta{X}=\cos(\phi_f)\cos(\lambda_f) - \cos(\phi_s)\cos(\lambda_s);\\ &\Delta{Y}=\cos(\phi_f)\sin(\lambda_f) - \cos(\phi_s)\sin(\lambda_s);\\ &\Delta{Z}=\sin(\phi_f) - \sin(\phi_s);\\ &C_h=\sqrt{(\Delta{X})^2+(\Delta{Y})^2+(\Delta{Z})^2} \end{align}\,\!$

The central angle is:

$\Delta\widehat{\sigma}=2\arcsin\left(\frac{C_h}{2}\right).\,\!$

The great circle distance is:

$d = r \Delta\widehat{\sigma}.\,\!$

Spherical cosine for sides derivation

By using Cartesian products rather than differences, the origin of the spherical cosine for sides becomes apparent:

$\begin{align} {\scriptstyle{\Pi}}X&=\cos(\phi_s)\cos(\phi_f)\cos(\lambda_s)\cos(\lambda_f);\\ {\scriptstyle{\Pi}}Y&=\cos(\phi_s)\cos(\phi_f)\sin(\lambda_s)\sin(\lambda_f);\\ {\scriptstyle{\Pi}}Z&=\sin(\phi_s)\sin(\phi_f);\\ \cos(\Delta\lambda)&=\frac{{\scriptstyle{\Pi}}X\!\!+\!{\scriptstyle{\Pi}}Y}{\cos(\phi_s)\cos(\phi_f)}=\cos(\lambda_s)\cos(\lambda_f)+\sin(\lambda_s)\sin(\lambda_f);\\ \Delta\widehat{\sigma}&=\arccos\Big({\scriptstyle{\Pi}}X+{\scriptstyle{\Pi}}Y+{\scriptstyle{\Pi}}Z\Big) =\arccos\Big({\scriptstyle{\Pi}}Z+\big({\scriptstyle{\Pi}}X+{\scriptstyle{\Pi}}Y\big)\Big),\\ &=\arccos\Big(\sin(\phi_s)\sin(\phi_f)+\cos(\phi_s)\cos(\phi_f)\cos(\Delta\lambda)\Big) .\end{align}\,\!$

Radius for spherical Earth

See also: Earth radius

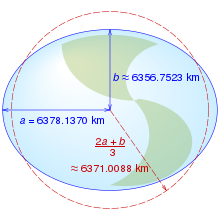
The shape of the Earth closely resembles a flattened sphere (a spheroid) with equatorial radius $a$ of 6,378.137 km; distance $b$ from the center of the spheroid to each pole is 6356.752 km. When calculating the length of a short north-south line at the equator, the sphere that best approximates that part of the spheroid has a radius of $b^2/a$ (which equals the meridian's semi-latus rectum), or 6,335.439 km, while the spheroid at the poles is best approximated by a sphere of radius $a^2/b$, or 6,399.594 km, a 1% difference. So as long as we're assuming a spherical Earth, any single formula for distance on the Earth is only guaranteed correct within 0.5% (though we can do better if our formula is only intended to apply to a limited area). There are different approximations used as a radius for a non-spherical body such as Earth:

• the average geocentric radius (≈(a+b)/2) or (ab)^.5;
• the equatorial radius (a);
• the volume and total surface area radius (≈(2a+b)/3 or (a²b)^1/3);;
• the average great circle circumference (≈(3a+b)/4 or (a³b)^.5).

McCaw recommends just using the volume/surface area based approximation (for Earth, approximately 6371.01 km).

Worked example

For an example of the formula in practice, take the latitude and longitude of two airports:

• Nashville International Airport (BNA) in Nashville, TN, USA: N 36°7.2', W 86°40.2'
• Los Angeles International Airport (LAX) in Los Angeles, CA, USA: N 33°56.4', W 118°24.0'

First convert the co-ordinates to decimal degrees

• BNA: $\;\phi_s=36.12^\circ \quad\lambda_s=-86.67^\circ\;\!$
• LAX: $\;\phi_f=33.94^\circ \quad\lambda_f=-118.40^\circ\;\!$

Plug these values into the spherical law of cosines: $\cos\Delta\widehat{\sigma}=\sin\phi_s\sin\phi_f+\cos\phi_s\cos\phi_f\cos\Delta\lambda\,\!$

$\Delta\widehat{\sigma}$ comes out to be 25.958 degrees, or 0.45306 radians, and the great-circle distance is the assumed radius times that angle:

$r\,\Delta\widehat{\sigma}\approx 6372.8 \times 0.45306 \approx 2887.26\mbox{ km}.\;\!$

So assuming a spherical earth, distance between LAX and BNA is about 2887 km or 1794 statute miles (× 0.621371) or 1559 nautical miles (× 0.539957). Geodesic distance between the given coordinates on the GRS 80/WGS 84 spheroid is 2892.777 km.

See also

• Air navigation
• Central angle
• Circumnavigation
• Flight planning
• Geodesy
• Geodetic system
• Geographical distance
• Great-circle navigation
• Haversine formula
• Meridian arc
• Qibla
• Spherical Earth
• Spherical geometry
• Spherical trigonometry
• Vincenty's formulae

External links

• GreatCircle at MathWorld

• Haversine formula in JavaScript Haversine and other formulae for calculating distances, bearings, etc.

• Distance Between Two Cities Site uses Haversine Formulae and integrates Road distances too