Circumference

Part of a series of articles on the
mathematical constant π
Uses
Area of disk Circumference Use in other formulae
Properties
Irrationality Transcendence
Value
Less than 22/7 Approximations Memorization
People
Archimedes Liu Hui Zu Chongzhi Aryabhata Madhava Ludolph van Ceulen Seki Takakazu Takebe Katahiro William Jones John Machin William Shanks John Wrench Chudnovsky brothers Yasumasa Kanada
History
Chronology Book
In culture
Legislation Holiday
Related topics
Squaring the circle Basel problem Feynman point Other topics related to π

Circumference (from Latin circumferentia, meaning "carrying around") is the linear distance around the edge of a closed curve or circular object. The circumference of a circle is of special importance in geometry and trigonometry. Informally "circumference" may also refer to the edge itself rather than to the length of the edge. Circumference is a special case of perimeter: the perimeter is the length around any closed figure, but conventionally "perimeter" is typically used in reference to a polygon while "circumference" typically refers to a continuously differentiable curve.

Circumference of a circle

Circle illustration with circumference (C) in black, diameter (D) in cyan, radius (R) in red, and centre or origin (O) in magenta. Circumference = π × diameter = 2 × π × radius.

The circumference of a circle is the distance around it. The term is used when measuring physical objects, as well as when considering abstract geometric forms.

When a circle's radius is 1, its circumference is 2π.

When a circle's diameter is 1, its circumference is π.

Relationship with Pi

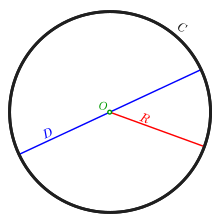
The circumference of a circle relates to one of the most important mathematical constants in all of mathematics. This constant, pi, is represented by the Greek letter π. The numerical value of π is 3.14159 26535 89793 ... (see  A000796). Pi is defined as the ratio of a circle's circumference to its diameter, or equivalently as the ratio of the circumference to twice the radius. Thus

${C}=\pi\cdot{d}=2\pi\cdot{r}.\!$

The use of the mathematical constant π is ubiquitous in mathematics, engineering, and science. While the constant ratio of circumference to radius ${C}/{r} = 2\pi$ also has many uses in mathematics, engineering, and science, it is not formally named. These uses include but are not limited to radians, computer programming, and physical constants.

Circumference of an ellipse

The circumference of an ellipse can be expressed in terms of the complete elliptic integral of the second kind.

Circumference of a graph

In graph theory the circumference of a graph refers to the longest cycle contained in that graph.

See also

• Arclength
• Area
• Caccioppoli set
• Isoperimetric inequality
• Pythagorean Theorem
• Volume

External links

• Numericana - Circumference of an ellipse
• Circumference of a circle With interactive applet and animation