Heronian triangle
In geometry, a Heronian triangle (or Heron triangle) is a triangle whose side lengths a, b, and c and area A are all positive integers.[1][2] Heronian triangles are named after Heron of Alexandria, based on their relation to Heron's formula which Heron demonstrated with the example triangle of sides 13, 14, 15 and area 84.[3]
Heron's formula implies that the Heronian triangles are exactly the positive integer solutions of the Diophantine equation
that is, the side lengths and area of any Heronian triangle satisfy the equation, and any positive integer solution of the equation describes a Heronian triangle.[4]
If the three side lengths are setwise coprime (meaning that the greatest common divisor of all three sides is 1), the Heronian triangle is called primitive.
Triangles whose side lengths and areas are all rational numbers (positive rational solutions of the above equation) are sometimes also called Heronian triangles or rational triangles;[5] in this article, these more general triangles will be called rational Heronian triangles. Every (integral) Heronian triangle is a rational Heronian triangle. Conversely, every rational Heronian triangle is similar to exactly one primitive Heronian triangle.
In any rational Heronian triangle, the three altitudes, the circumradius, the inradius and exradii, and the sines and cosines of the three angles are also all rational numbers.
Scaling to primitive triangles[edit]
Scaling a triangle with a factor of s consists of multiplying its side lengths by s; this multiplies the area by and produces a similar triangle. Scaling a rational Heronian triangle by a rational factor produces another rational Heronian triangle.
Given a rational Heronian triangle of side lengths the scale factor produce a rational Heronian triangle such that its side lengths are setwise coprime integers. It is proved below that the area A is an integer, and thus the triangle is a Heronian triangle. Such a triangle is often called a primitive Heronian triangle.
In summary, every similarity class of rational Heronian triangles contains exactly one primitive Heronian triangle. A byproduct of the proof is that exactly one of the side lengths of a primitive Heronian triangle is an even integer.
Proof: One has to prove that, if the side lengths of a rational Heronian triangle are coprime integers, then the area A is also an integer and exactly one of the side lengths is even.
The Diophantine equation given in the introduction shows immediately that is an integer. Its square root is also an integer, since the square root of an integer is either an integer or an irrational number.
If exactly one of the side lengths is even, all the factors in the right-hand side of the equation are even, and, by dividing the equation by 16, one gets that and are integers.
As the side lengths are supposed to be coprime, one is left with the case where one or three side lengths are odd. Supposing that c is odd, the right-hand side of the Diophantine equation can be rewritten
with and even. As the square of an odd integer is congruent to modulo 4, the right-hand side of the equation must be congruent to modulo 4. It is thus impossible, that one has a solution of the Diophantine equation, since must be the square of an integer, and the square of an integer is congruent to 0 or 1 modulo 4.
Examples[edit]
Any Pythagorean triangle is a Heronian triangle. The side lengths of such a triangle are integers, by definition. In any such triangle, one of the two shorter sides has even length, so the area (the product of these two sides, divided by two) is also an integer.
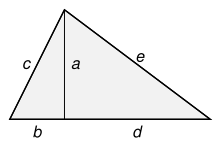
Examples of Heronian triangles that are not right-angled are the isosceles triangle obtained by joining a Pythagorean triangle and its mirror image along a side of the right angle. Starting with the Pythagorean triple 3, 4, 5 this gives two Heronian triangles with side lengths (5, 5, 6) and (5, 5, 8) and area 12.
More generally, given two Pythagorean triples and with largest entries c and e, one can join the corresponding triangles along the sides of length a (see the figure) for getting a Heronian triangle with side lengths and area (this is an integer, since the area of a Pythagorean triangle is an integer).
There are Heronian triangles that cannot be obtained by joining Pythagorean triangles. For example, the Heronian triangle of side lengths and area 72, since none of its altitudes is an integer. Such Heronian triangles are known as indecomposable.[6] However, every Heronian triangle can be constructed from right triangles with rational side lengths, and is thus similar to a decomposable Heronian triangle. In fact, at least one of the altitudes of a triangle is inside the triangle, and divides it into two right triangles. These triangles have rational sides, since the cosine and the sine of the angles of a Heronian triangle are rational numbers, and, with notation of the figure, one has and where is the left-most angle of the triangle.
Rationality properties[edit]
Many quantities related to a Heronian triangle are rational numbers. In particular:
- All the altitudes of a Heronian triangle are rational.[7] This can be seen from the fact that the area of a triangle is half of one side times its altitude from that side, and a Heronian triangle has integer sides and area. Some Heronian triangles have three non-integer altitudes, for example the acute (15, 34, 35) with area 252 and the obtuse (5, 29, 30) with area 72. Any Heronian triangle with one or more non-integer altitudes can be scaled up by a factor equalling the least common multiple of the altitudes' denominators in order to obtain a similar Heronian triangle with three integer altitudes.
- All the interior perpendicular bisectors of a Heronian triangle are rational: For any triangle these are given by and where the sides are a ≥ b ≥ c and the area is A;[8] in a Heronian triangle all of a, b, c, and A are integers.
- Every interior angle of a Heronian triangle has a rational sine. This follows from the area formula Area = (1/2)ab sin C, in which the area and the sides a and b are integers, and equivalently for the other interior angles.
- Every interior angle of a Heronian triangle has a rational cosine. This follows from the law of cosines , c2 = a2 + b2 − 2ab cos C, in which the sides a, b, and c are integers, and equivalently for the other interior angles.
- Because all Heronian triangles have all interior angles' sines and cosines rational, this implies that the tangent, cotangent, secant, and cosecant of each interior angle is either rational or infinite.
- Half of each interior angle has a rational tangent because tan C/2 = sin C / (1 + cos C), and equivalently for other interior angles. Knowledge of these half-angle tangent values is sufficient to reconstruct the side lengths of a primitive Heronian triangle (see below).
- For any triangle, the angle spanned by a side as viewed from the center of the circumcircle is twice the interior angle of the triangle vertex opposite the side. Because the half-angle tangent for each interior angle of a Heronian triangle is rational, it follows that the quarter-angle tangent of each such central angle of a Heronian triangle is rational. (Also, the quarter-angle tangents are rational for the central angles of a Brahmagupta quadrilateral, but is an unsolved problem whether this is true for all Robbins pentagons.) The reverse is true for all cyclic polygons generally; if all such central angles have rational tangents for their quarter angles then the cyclic polygon can be scaled to simultaneously have integer area, sides, and diagonals (connecting any two vertices).
- There are no Heronian triangles whose three internal angles form an arithmetic progression. This is because all plane triangles with interior angles in an arithmetic progression must have one interior angle of 60°, which does not have a rational sine.[9]
- Any square inscribed in a Heronian triangle has rational sides: For a general triangle the inscribed square on side of length a has length where A is the triangle's area;[10] in a Heronian triangle, both A and a are integers.
- Every Heronian triangle has a rational inradius (radius of its inscribed circle): For a general triangle the inradius is the ratio of the area to half the perimeter, and both of these are rational in a Heronian triangle.
- Every Heronian triangle has a rational circumradius (the radius of its circumscribed circle): For a general triangle the circumradius equals one-fourth the product of the sides divided by the area; in a Heronian triangle the sides and area are integers.
- In a Heronian triangle the distance from the centroid to each side is rational because, for all triangles, this distance is the ratio of twice the area to three times the side length.[11] This can be generalized by stating that all centers associated with Heronian triangles whose barycentric coordinates are rational ratios have a rational distance to each side. These centers include the circumcenter, orthocenter, nine-point center, symmedian point, Gergonne point and Nagel point.[12]
- Every Heronian triangle can be placed on a unit-sided square lattice with each vertex at a lattice point.[13] As a corollary, every rational Heronian triangle can be placed into a two-dimensional Cartesian coordinate system with all rational-valued coordinates.
Properties of side lengths[edit]
Here are some properties of side lengths of Heronian triangles, whose side lengths are a, b, c and area is A.
- Every primitive Heronian triangle Heronian triangle has one even and two odd sides (see § Scaling to primitive triangles). It follows that a Heronian triangle has either one or three sides of even length,[14]: p.3 and that the perimeter of a primitive Heronian triangle is always an even number.[15]
- There are no equilateral Heronian triangles, since a primitive Heronian triangle has one even side length and two odd side lengths.[7]
- The area of a Heronian triangle is always divisible by 6.[16][15]
- There are no Heronian triangles with a side length of either 1 or 2.[17][1]
- There exist an infinite number of primitive Heronian triangles with one side length equal to a given a, provided that a > 2.[1]
- The semiperimeter s of a Heronian triangle cannot be prime (as is the square of the area, and the area is an integer, if s were prime, it would divide another factor; this is impossible as these factors are all less than s).
- In a Heronian triangles that has no integer altitude (indecomposable and non-Pythagorean), all side lengths have a prime factor of the form 4k+1.[6] In a primitive Pythagoran triangle, all prime factors of the hypothenuse have the form 4k+1. A decomposable Heronian triangle must have two sides that are the hypotenuse of a Pythagorean triangle, and thus two sides that have prime factors of the form 4k+1. There may also be prime factors of the form 4k+3, since the Pythagorean components of a decomposable Heronian triangle need not to be primitive, even if the Heronian triangle is primitive. In summary, all Heronian triangles have at least one side that is divisible by a prime of the form 4k+1.
- There are no Heronian triangles whose side lengths form a geometric progression.[18]
- If any two sides (but not three) of a Heronian triangle have a common factor, that factor must be the sum of two squares.[19]
Parametrizations[edit]
A parametric equation or parametrization of Heronian triangles consists of an expression of the side lengths and area of a triangle as functions—typically polynomial functions – of some parameters, such that the triangle is Heronian if and only if the parameters satisfy some constraints—typically, to be positive integers satisfying some inequalities. It is also generally required that all Heronian triangles can be obtained up to a scaling for some values of the parameters, and that these values are unique, if an order on the sides of the triangle is specified.
The first such parametrization was discovered by Brahmagupta (598-668 A.D.), who did not prove that all Heronian triangles can be generated by the parametrization. In the 18th century, Leonard Euler provided another parametrization and proved that it generates all Heronian triangles. These parametrizations are described in the next two subsections.
In the third subsection, a rational parametrization—that is a parametrization where the parameters are positive rational numbers—is naturally derived from properties of Heronian triangles. Both Brahmagupta's and Euler's parametrizations can be recovered from this rational parametrization by clearing denominators. This provides a proof that Brahmagupta's and Euler's parametrizations generate all Heronian triangles.
Brahmagupta's parametric equation[edit]
The Indian mathematician Brahmagupta (598-668 A.D.) discovered the following parametric equations for generating Heronian triangles,[20] but did not prove that every similarity class of Heronian triangles can be obtained this way.[citation needed]
For three positive integers m, n and k that are setwise coprime () and satisfy (to guarantee positive side lengths) and (for uniqueness):
where s is the semiperimeter, A is the area, and r is the inradius.
The resulting Heronian triangle is not always primitive, and a scaling may be needed for getting the corresponding primitive triangle. For example, taking m = 36, n = 4 and k = 3 produces a triangle with a = 5220, b = 900 and c = 5400, which is similar to the (5, 29, 30) Heronian triangle with a proportionality factor of 180.
The fact that the generated triangle is not primitive is an obstacle for using this parametrization for generating all Heronian triangles with size lengths less than a given bound (since the size of cannot be predicted.[20]
Euler's parametric equation[edit]
The following method of generating all Heronian triangles was discovered by Leonard Euler,[21] who was the first to provably parametrize all such triangles.
For four positive integers m coprime to n and p coprime to q () satisfying (to guarantee positive side lengths):
where s is the semiperimeter, A is the area, and r is the inradius.
Even when m, n, p, and q are pairwise coprime, the resulting Heronian triangle may not be primitive. In particular, if m, n, p, and q are all odd, the three side lengths are even. It is also possible that a, b, and c have a common divisor other than 2. For example, with m = 2, n = 1, p = 7, and q = 4, one gets (a, b, c) = (130, 140, 150), where each side length is a multiple of 10; the corresponding primitive triple is (13, 14, 15), which can also be obtained by dividing the triple resulting from m = 2, n = 1, p = 3, q = 2 by two, then exchanging b and c.
Half-angle tangent parametrization[edit]
Let be the side lengths of a triangle, let be the interior angles opposite these sides, and let and be the half-angle tangents. The values are all positive and satisfy ; this "triple tangent identity" is the half-angle tangent version of the fundamental triangle identity written as radians (that is, 90°), as can be proved using the addition formula for tangents. By the laws of sines and cosines, all of the sines and the cosines of are rational numbers if the triangle is a rational Heronian triangle and, because a half-angle tangent is a rational function of the sine and cosine, it follows that the half-angle tangents are also rational.
Conversely, if are positive rational numbers such that it can be seen that they are the half-angle tangents of the interior angles of a class of similar Heronian triangles.[22] The condition can be rearranged to and the restriction requires Thus there is a bijection between the similarity classes of rational Heronian triangles and the pairs of positive rational numbers whose product is less than 1.
To make this bijection explicit, one can choose, as a specific member of the similarity class, the triangle inscribed in a unit-diameter circle with side lengths equal to the sines of the opposite angles:[23]
where is the semiperimeter, is the area, is the inradius, and all these values are rational because and are rational.
To obtain an (integral) Heronian triangle, the denominators of a, b, and c must be cleared. There are several ways to do this. If and with (irreducible fractions), and the triangle is scaled up by the result is Euler's parametrization. If and with (lowest common denomimator), and the triangle is scaled up by the result is similar but not quite identical to Brahmagupta's parametrization. If, instead, this is and that are reduced to the lowest common denominator, that is, if and with then one gets exactly Brahmagupta's parametrization by scaling up the triangle by
This proves that either parametrization generates all Heronian triangles.
Other results[edit]
Kurz (2008) has derived fast algorithms for generating Heronian triangles.
There are infinitely many primitive and indecomposable non-Pythagorean Heronian triangles with integer values for the inradius and all three of the exradii , including the ones generated by[24]: Thm. 4
There are infinitely many Heronian triangles that can be placed on a lattice such that not only are the vertices at lattice points, as holds for all Heronian triangles, but additionally the centers of the incircle and excircles are at lattice points.[24]: Thm. 5
See also Integer triangle § Heronian triangles for parametrizations of some types of Heronian triangles.
Examples[edit]
The list of primitive integer Heronian triangles, sorted by area and, if this is the same, by perimeter, starts as in the following table. "Primitive" means that the greatest common divisor of the three side lengths equals 1.
| Area | Perimeter | side length b+d | side length e | side length c |
|---|---|---|---|---|
| 6 | 12 | 5 | 4 | 3 |
| 12 | 16 | 6 | 5 | 5 |
| 12 | 18 | 8 | 5 | 5 |
| 24 | 32 | 15 | 13 | 4 |
| 30 | 30 | 13 | 12 | 5 |
| 36 | 36 | 17 | 10 | 9 |
| 36 | 54 | 26 | 25 | 3 |
| 42 | 42 | 20 | 15 | 7 |
| 60 | 36 | 13 | 13 | 10 |
| 60 | 40 | 17 | 15 | 8 |
| 60 | 50 | 24 | 13 | 13 |
| 60 | 60 | 29 | 25 | 6 |
| 66 | 44 | 20 | 13 | 11 |
| 72 | 64 | 30 | 29 | 5 |
| 84 | 42 | 15 | 14 | 13 |
| 84 | 48 | 21 | 17 | 10 |
| 84 | 56 | 25 | 24 | 7 |
| 84 | 72 | 35 | 29 | 8 |
| 90 | 54 | 25 | 17 | 12 |
| 90 | 108 | 53 | 51 | 4 |
| 114 | 76 | 37 | 20 | 19 |
| 120 | 50 | 17 | 17 | 16 |
| 120 | 64 | 30 | 17 | 17 |
| 120 | 80 | 39 | 25 | 16 |
| 126 | 54 | 21 | 20 | 13 |
| 126 | 84 | 41 | 28 | 15 |
| 126 | 108 | 52 | 51 | 5 |
| 132 | 66 | 30 | 25 | 11 |
| 156 | 78 | 37 | 26 | 15 |
| 156 | 104 | 51 | 40 | 13 |
| 168 | 64 | 25 | 25 | 14 |
| 168 | 84 | 39 | 35 | 10 |
| 168 | 98 | 48 | 25 | 25 |
| 180 | 80 | 37 | 30 | 13 |
| 180 | 90 | 41 | 40 | 9 |
| 198 | 132 | 65 | 55 | 12 |
| 204 | 68 | 26 | 25 | 17 |
| 210 | 70 | 29 | 21 | 20 |
| 210 | 70 | 28 | 25 | 17 |
| 210 | 84 | 39 | 28 | 17 |
| 210 | 84 | 37 | 35 | 12 |
| 210 | 140 | 68 | 65 | 7 |
| 210 | 300 | 149 | 148 | 3 |
| 216 | 162 | 80 | 73 | 9 |
| 234 | 108 | 52 | 41 | 15 |
| 240 | 90 | 40 | 37 | 13 |
| 252 | 84 | 35 | 34 | 15 |
| 252 | 98 | 45 | 40 | 13 |
| 252 | 144 | 70 | 65 | 9 |
| 264 | 96 | 44 | 37 | 15 |
| 264 | 132 | 65 | 34 | 33 |
| 270 | 108 | 52 | 29 | 27 |
| 288 | 162 | 80 | 65 | 17 |
| 300 | 150 | 74 | 51 | 25 |
| 300 | 250 | 123 | 122 | 5 |
| 306 | 108 | 51 | 37 | 20 |
| 330 | 100 | 44 | 39 | 17 |
| 330 | 110 | 52 | 33 | 25 |
| 330 | 132 | 61 | 60 | 11 |
| 330 | 220 | 109 | 100 | 11 |
| 336 | 98 | 41 | 40 | 17 |
| 336 | 112 | 53 | 35 | 24 |
| 336 | 128 | 61 | 52 | 15 |
| 336 | 392 | 195 | 193 | 4 |
| 360 | 90 | 36 | 29 | 25 |
| 360 | 100 | 41 | 41 | 18 |
| 360 | 162 | 80 | 41 | 41 |
| 390 | 156 | 75 | 68 | 13 |
| 396 | 176 | 87 | 55 | 34 |
| 396 | 198 | 97 | 90 | 11 |
| 396 | 242 | 120 | 109 | 13 |
Lists of primitive Heronian triangles whose sides do not exceed 6,000,000 can be found at "Lists of primitive Heronian triangles". Sascha Kurz, University of Bayreuth, Germany. Archived (PDF) from the original on 2016-05-08. Retrieved 29 March 2016.
Heronian triangles with perfect square sides[edit]
Heronian triangles with perfect square sides are related to the Perfect cuboid problem. As of February 2021, only two primitive Heronian triangles with perfect square sides are known:
(1853², 4380², 4427², Area=32918611718880), published in 2013.[25]
(11789², 68104² , 68595², Area=284239560530875680), published in 2018.[26]
Equable triangles[edit]
A shape is called equable if its area equals its perimeter. There are exactly five equable Heronian triangles: the ones with side lengths (5,12,13), (6,8,10), (6,25,29), (7,15,20), and (9,10,17),[27][28] though only four of them are primitive.
Almost-equilateral Heronian triangles[edit]
Since the area of an equilateral triangle with rational sides is an irrational number, no equilateral triangle is Heronian. However, a sequence of isosceles Heronian triangles that are "almost equilateral" can be developed from the duplication of right-angled triangles, in which the hypotenuse is almost twice as long as one of the legs. The first few examples of these almost-equilateral triangles are listed in the following table (sequence A102341 in the OEIS):
| Side length | Area | ||
|---|---|---|---|
| a | b=a | c | |
| 5 | 5 | 6 | 12 |
| 17 | 17 | 16 | 120 |
| 65 | 65 | 66 | 1848 |
| 241 | 241 | 240 | 25080 |
| 901 | 901 | 902 | 351780 |
| 3361 | 3361 | 3360 | 4890480 |
| 12545 | 12545 | 12546 | 68149872 |
| 46817 | 46817 | 46816 | 949077360 |
There is a unique sequence of Heronian triangles that are "almost equilateral" because the three sides are of the form n − 1, n, n + 1. A method for generating all solutions to this problem based on continued fractions was described in 1864 by Edward Sang,[29] and in 1880 Reinhold Hoppe gave a closed-form expression for the solutions.[30] The first few examples of these almost-equilateral triangles are listed in the following table (sequence A003500 in the OEIS):
| Side length | Area | Inradius | ||
|---|---|---|---|---|
| n − 1 | n | n + 1 | ||
| 3 | 4 | 5 | 6 | 1 |
| 13 | 14 | 15 | 84 | 4 |
| 51 | 52 | 53 | 1170 | 15 |
| 193 | 194 | 195 | 16296 | 56 |
| 723 | 724 | 725 | 226974 | 209 |
| 2701 | 2702 | 2703 | 3161340 | 780 |
| 10083 | 10084 | 10085 | 44031786 | 2911 |
| 37633 | 37634 | 37635 | 613283664 | 10864 |
Subsequent values of n can be found by multiplying the previous value by 4, then subtracting the value prior to that one (52 = 4 × 14 − 4, 194 = 4 × 52 − 14, etc.), thus:
where t denotes any row in the table. This is a Lucas sequence. Alternatively, the formula generates all n for positive integers t. Equivalently, let A = area and y = inradius, then,
where {n, y} are solutions to n2 − 12y2 = 4. A small transformation n = 2x yields a conventional Pell equation x2 − 3y2 = 1, the solutions of which can then be derived from the regular continued fraction expansion for √3.[31]
The variable n is of the form , where k is 7, 97, 1351, 18817, .... The numbers in this sequence have the property that k consecutive integers have integral standard deviation.[32]
See also[edit]
References[edit]
- ^ a b c Carlson, John R. (1970), "Determination of Heronian Triangles" (PDF), Fibonacci Quarterly, 8: 499–506
- ^ Beauregard, Raymond A.; Suryanarayan, E. R. (January 1998), "The Brahmagupta Triangles" (PDF), College Mathematics Journal, 29 (1): 13–17, doi:10.2307/2687630, JSTOR 2687630
- ^ Sastry, K. R. S. (2001). "Heron triangles: A Gergonne-Cevian-and-median perspective" (PDF). Forum Geometricorum. 1 (2001): 17–24.
- ^ The sides and area of any triangle satisfy the Diophantine equation obtained by squaring both sides of Heron's formula; see Heron's formula § Proofs. Conversely, consider a solution of the equation where are all positive integers. It corresponds to a valid triangle if and only if the triangle inequality is satisfied, that is, if the three integers and are all positive. This is necessarily true in this case: if any of these sums were negative or zero, the other two would be positive and the right-hand side of the equation would thus be negative or zero and could not possibly equal the left-hand side which is positive.
- ^ Weisstein, Eric W. "Heronian Triangle". MathWorld.
- ^ a b Yiu, Paul (2008), Heron triangles which cannot be decomposed into two integer right triangles (PDF), 41st Meeting of Florida Section of Mathematical Association of America
- ^ a b Somos, M. (December 2014). "Rational triangles". Retrieved 2018-11-04.
- ^ Mitchell, Douglas W. (2013), "Perpendicular Bisectors of Triangle Sides", Forum Geometricorum 13, 53−59: Theorem 2.
- ^ Zelator, K., "Triangle Angles and Sides in Progression and the diophantine equation x2+3y2=z2", Cornell Univ. archive, 2008
- ^ Bailey, Herbert, and DeTemple, Duane, "Squares inscribed in angles and triangles", Mathematics Magazine 71(4), 1998, 278–284.
- ^ Clark Kimberling, "Trilinear distance inequalities for the symmedian point, the centroid, and other triangle centers", Forum Geometricorum, 10 (2010), 135−139. http://forumgeom.fau.edu/FG2010volume10/FG201015index.html
- ^ Clark Kimberling's Encyclopedia of Triangle Centers "Encyclopedia of Triangle Centers". Retrieved 2012-06-17.
- ^ Yiu, Paul (2001). "Heronian triangles are lattice triangles". The American Mathematical Monthly. 108 (3): 261–263. doi:10.1080/00029890.2001.11919751.
- ^ Buchholz, Ralph H.; MacDougall, James A. "Cyclic Polygons with Rational Sides and Area". Journal of Number Theory. 128 (1): 17–48. doi:10.1016/j.jnt.2007.05.005.
- ^ a b Fricke, Jan (2002-12-21). "On Heron Simplices and Integer Embedding". arXiv:math/0112239.
- ^ Proof. One can suppose that the Heronian triangle is primitive. The right-hand side of the Diophantine equation can be rewritten as If an odd length is chosen for c, all squares are odd, and therefore of the form and the two differences are multiple of 8. So is multiple of 64, and A is even. For the divisibility by three, one chooses c as non-multiple of 3 (the triangle is supposed to be primitive). If one of and is not a multiple of 3, the corresponding factor is a nultiple of 3 (since the square of a non-multiple of 3 has the form ), and this implies that 3 is a divisor of Otherwise, 3 would divide both and and the right-hand side of the Diophantine would not be the square of as being congruent to minus times a square modulo 3. So this last case is impossible.
- ^ Proof. Supposing the triangle inequality implies If this implies that and the condition that there is exactly one even side length cannot be fulfilled. If one has two even side lengths if So, and the Diophantine equation becomes which is impossible for two positive integers.
- ^ Buchholz, Ralph H.; MacDougall, James A. (1999). "Heron Quadrilaterals with sides in Arithmetic or Geometric progression". Bulletin of the Australian Mathematical Society. 59 (2): 263–269. doi:10.1017/s0004972700032883. hdl:1959.13/803798.
- ^ Blichfeldt, H. F. (1896–1897). "On Triangles with Rational Sides and Having Rational Areas". Annals of Mathematics. 11 (1/6): 57–60. doi:10.2307/1967214. JSTOR 1967214.
- ^ a b Kurz, Sascha (2008). "On the generation of Heronian triangles". Serdica Journal of Computing. 2 (2): 181–196. arXiv:1401.6150. Bibcode:2014arXiv1401.6150K. doi:10.55630/sjc.2008.2.181-196. MR 2473583. S2CID 16060132..
- ^ Dickson 1920, p. 193.
- ^ Cheney, William Fitch Jr. (1929). "Heronian Triangles" (PDF). American Mathematical Monthly. 36 (1): 22–28. doi:10.1080/00029890.1929.11986902.
- ^ Kocik, Jerzy; Solecki, Andrzej (2009). "Disentangling a triangle" (PDF). American Mathematical Monthly. 116 (3): 228–237. doi:10.1080/00029890.2009.11920932. S2CID 28155804.
- ^ a b Zhou, Li, "Primitive Heronian Triangles With Integer Inradius and Exradii", Forum Geometricorum 18, 2018, 71-77. http://forumgeom.fau.edu/FG2018volume18/FG201811.pdf
- ^ Stănică, Pantelimon; Sarkar, Santanu; Sen Gupta, Sourav; Maitra, Subhamoy; Kar, Nirupam (2013). "Counting Heron triangles with constraints". Integers. 13: Paper No. A3, 17pp. hdl:10945/38838. MR 3083465.
- ^ "LISTSERV - NMBRTHRY Archives - LISTSERV.NODAK.EDU".
- ^ Dickson 1920, p. 199.
- ^ Markowitz, L. (1981), "Area = Perimeter", The Mathematics Teacher, 74 (3): 222–3, doi:10.5951/MT.74.3.0222
- ^ Sang, Edward (1864), "On the theory of commensurables", Transactions of the Royal Society of Edinburgh, 23 (3): 721–760, doi:10.1017/s0080456800020019, S2CID 123752318. See in particular p. 734.
- ^ Gould, H. W. (February 1973), "A triangle with integral sides and area" (PDF), Fibonacci Quarterly, 11 (1): 27–39.
- ^ Richardson, William H. (2007), Super-Heronian Triangles
- ^ Online Encyclopedia of Integer Sequences, OEIS: A011943.
Further reading[edit]
- Carmichael, Robert Daniel (1915). "I. Introduction. Rational Triangles. Method of Infinite Descent". Diophantine Analysis. Wiley. pp. 1–23.
- Dickson, Leonard Eugene (1920). "V. Triangles, Quadrilaterals, and Tetrahedra with Rational Sides". History of the Theory of Numbers, Volume II: Diophantine Analysis. Carnegie Institution of Washington. pp. 191–224.
External links[edit]
- Weisstein, Eric W. "Heronian triangle". MathWorld.
- Online Encyclopedia of Integer Sequences Heronian
- S. sh. Kozhegel'dinov (1994), "On fundamental Heronian triangles", Math. Notes, 55 (2): 151–6, doi:10.1007/BF02113294, S2CID 115233024

















































![{\displaystyle {\begin{aligned}a&=\sin \alpha ={\frac {2t}{1+t^{2}}},&s-a={\frac {2u(1-tu)}{(1+t^{2})(1+u^{2})}},\\[5mu]b&=\sin \beta ={\frac {2u}{1+u^{2}}},&s-b={\frac {2t(1-tu)}{(1+t^{2})(1+u^{2})}},\\[5mu]c&=\sin \gamma ={\frac {2(t+u)(1-tu)}{(1+t^{2})(1+u^{2})}},&s-c={\frac {2tu(t+u)}{(1+t^{2})(1+u^{2})}},\\[5mu]&&s={\frac {2(t+u)}{(1+t^{2})(1+u^{2})}},\\A&={\frac {4tu(t+u)(1-tu)}{(1+t^{2})^{2}(1+u^{2})^{2}}},&r={\frac {2tu(1-tu)}{(1+t^{2})(1+u^{2})}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de7e22c0ee7991d810beae4ff9a454d8f2ef1f9)










































