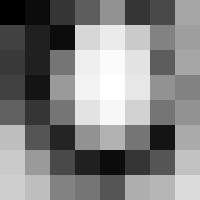Histogram equalization
This article's lead section may be too short to adequately summarize the key points. (November 2023) |
Histogram equalization is a method in image processing of contrast adjustment using the image's histogram.

Overview[edit]
This method usually increases the global contrast of many images, especially when the image is represented by a narrow range of intensity values. Through this adjustment, the intensities can be better distributed on the histogram utilizing the full range of intensities evenly. This allows for areas of lower local contrast to gain a higher contrast. Histogram equalization accomplishes this by effectively spreading out the highly populated intensity values which are used to degrade image contrast.
The method is useful in images with backgrounds and foregrounds that are both bright or both dark. In particular, the method can lead to better views of bone structure in x-ray images, and to better detail in photographs that are either over or under-exposed. A key advantage of the method is that it is a fairly straightforward technique adaptive to the input image and an invertible operator. So in theory, if the histogram equalization function is known, then the original histogram can be recovered. The calculation is not computationally intensive. A disadvantage of the method is that it is indiscriminate. It may increase the contrast of background noise, while decreasing the usable signal.
In scientific imaging where spatial correlation is more important than intensity of signal (such as separating DNA fragments of quantized length), the small signal-to-noise ratio usually hampers visual detections.
Histogram equalization often produces unrealistic effects in photographs; however it is very useful for scientific images like thermal, satellite or x-ray images, often the same class of images to which one would apply false-color. Also histogram equalization can produce undesirable effects (like visible image gradient) when applied to images with low color depth. For example, if applied to 8-bit image displayed with 8-bit gray-scale palette it will further reduce color depth (number of unique shades of gray) of the image. Histogram equalization will work the best when applied to images with much higher color depth than palette size, like continuous data or 16-bit gray-scale images.
There are two ways to think about and implement histogram equalization, either as image change or as palette change. The operation can be expressed as P(M(I)) where I is the original image, M is histogram equalization mapping operation and P is a palette. If we define a new palette as P'=P(M) and leave image I unchanged then histogram equalization is implemented as palette change or mapping change. On the other hand, if palette P remains unchanged and image is modified to I'=M(I) then the implementation is accomplished by image change. In most cases palette change is better as it preserves the original data.
Modifications of this method use multiple histograms, called subhistograms, to emphasize local contrast, rather than overall global contrast. Examples of such methods include adaptive histogram equalization, contrast limiting adaptive histogram equalization or CLAHE, multipeak histogram equalization (MPHE), and multipurpose beta optimized bihistogram equalization (MBOBHE). The goal of these methods, especially MBOBHE, is to improve the contrast without producing brightness mean-shift and detail loss artifacts by modifying the HE algorithm.[1]
A signal transform equivalent to histogram equalization also seems to happen in biological neural networks so as to maximize the output firing rate of the neuron as a function of the input statistics. This has been proved in particular in the fly retina.[2]
Histogram equalization is a specific case of the more general class of histogram remapping methods. These methods seek to adjust the image to make it easier to analyze or improve visual quality (e.g., retinex)
Back projection[edit]
The back projection (or "project") of a histogrammed image is the re-application of the modified histogram to the original image, functioning as a look-up table for pixel brightness values.
For each group of pixels taken from the same position from all input single-channel images, the function puts the histogram bin value to the destination image, where the coordinates of the bin are determined by the values of pixels in this input group. In terms of statistics, the value of each output image pixel characterizes the probability that the corresponding input pixel group belongs to the object whose histogram is used.[3]
Implementation[edit]
Consider a discrete grayscale image {x} and let ni be the number of occurrences of gray level i. The probability of an occurrence of a pixel of level i in the image is
being the total number of gray levels in the image (typically 256), n being the total number of pixels in the image, and being in fact the image's histogram for pixel value i, normalized to [0,1].
Let us also define the cumulative distribution function corresponding to i as
- ,
which is also the image's accumulated normalized histogram.
We would like to create a transformation of the form to produce a new image {y}, with a flat histogram. Such an image would have a linearized cumulative distribution function (CDF) across the value range, i.e.
- for
for some constant . The properties of the CDF allow us to perform such a transform (see Inverse distribution function); it is defined as
where is in the range . Notice that maps the levels into the range [0,1], since we used a normalized histogram of {x}. In order to map the values back into their original range, the following simple transformation needs to be applied on the result:
- .
A more detailed derivation is provided here.
is a real value while has to be an integer. An intuitive and popular method[4] is applying the round operation:
- .
However, detailed analysis results in slightly different formulation. The mapped value should be 0 for the range of . And for , for , ...., and finally for . Then the quantization formula from to should be
.
(Note: when , however, it does not happen just because means that there is no pixel corresponding to that value.)
Of color images[edit]
The above describes histogram equalization on a grayscale image. However it can also be used on color images by applying the same method separately to the Red, Green and Blue components of the RGB color values of the image. However, applying the same method on the Red, Green, and Blue components of an RGB image may yield dramatic changes in the image's color balance since the relative distributions of the color channels change as a result of applying the algorithm. However, if the image is first converted to another color space, Lab color space, or HSL/HSV color space in particular, then the algorithm can be applied to the luminance or value channel without resulting in changes to the hue and saturation of the image.[5] There are several histogram equalization methods in 3D space. Trahanias and Venetsanopoulos applied histogram equalization in 3D color space[6] However, it results in "whitening" where the probability of bright pixels are higher than that of dark ones.[7] Han et al. proposed to use a new cdf defined by the iso-luminance plane, which results in uniform gray distribution.[8]
Examples[edit]
For consistency with statistical usage, "CDF" (i.e. Cumulative distribution function) should be replaced by "cumulative histogram", especially since the article links to cumulative distribution function which is derived by dividing values in the cumulative histogram by the overall amount of pixels. The equalized CDF is defined in terms of rank as .
Small image[edit]
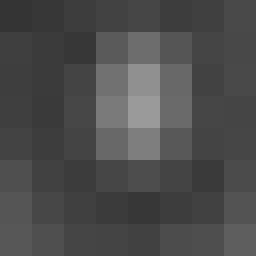
The 8-bit grayscale image shown has the following values:
| 52 | 55 | 61 | 59 | 79 | 61 | 76 | 61 |
|---|---|---|---|---|---|---|---|
| 62 | 59 | 55 | 104 | 94 | 85 | 59 | 71 |
| 63 | 65 | 66 | 113 | 144 | 104 | 63 | 72 |
| 64 | 70 | 70 | 126 | 154 | 109 | 71 | 69 |
| 67 | 73 | 68 | 106 | 122 | 88 | 68 | 68 |
| 68 | 79 | 60 | 70 | 77 | 66 | 58 | 75 |
| 69 | 85 | 64 | 58 | 55 | 61 | 65 | 83 |
| 70 | 87 | 69 | 68 | 65 | 73 | 78 | 90 |
The histogram for this image is shown in the following table. Pixel values that have a zero count are excluded for the sake of brevity.
Value Count Value Count Value Count Value Count Value Count 52 1 64 2 72 1 85 2 113 1 55 3 65 3 73 2 87 1 122 1 58 2 66 2 75 1 88 1 126 1 59 3 67 1 76 1 90 1 144 1 60 1 68 5 77 1 94 1 154 1 61 4 69 3 78 1 104 2 62 1 70 4 79 2 106 1 63 2 71 2 83 1 109 1
The cumulative distribution function (cdf) is shown below. Again, pixel values that do not contribute to an increase in the cdf are excluded for brevity.
(Please note that version is not illustrated yet.)v, Pixel Intensity cdf(v) h(v), Equalized v 52 1 0 55 4 12 58 6 20 59 9 32 60 10 36 61 14 53 62 15 57 63 17 65 64 19 73 65 22 85 66 24 93 67 25 97 68 30 117 69 33 130 70 37 146 71 39 154 72 40 158 73 42 166 75 43 170 76 44 174 77 45 178 78 46 182 79 48 190 83 49 194 85 51 202 87 52 206 88 53 210 90 54 215 94 55 219 104 57 227 106 58 231 109 59 235 113 60 239 122 61 243 126 62 247 144 63 251 154 64 255
This cdf shows that the minimum value in the subimage is 52 and the maximum value is 154. The cdf of 64 for value 154 coincides with the number of pixels in the image. The cdf must be normalized to . The general histogram equalization formula is:
where cdfmin is the minimum non-zero value of the cumulative distribution function (in this case 1), M × N gives the image's number of pixels (for the example above 64, where M is width and N the height) and L is the number of grey levels used (in most cases, like this one, 256).
Note that to scale values in the original data that are above 0 to the range 1 to L-1, inclusive, the above equation would instead be:
where cdf(v) > 0. Scaling from 1 to 255 preserves the non-zero-ness of the minimum value.
The equalization formula for the example scaling data from 0 to 255, inclusive, is:
For example, the cdf of 78 is 46. (The value of 78 is used in the bottom row of the 7th column.) The normalized value becomes
Once this is done then the values of the equalized image are directly taken from the normalized cdf to yield the equalized values:
| 0 | 12 | 53 | 32 | 190 | 53 | 174 | 53 |
|---|---|---|---|---|---|---|---|
| 57 | 32 | 12 | 227 | 219 | 202 | 32 | 154 |
| 65 | 85 | 93 | 239 | 251 | 227 | 65 | 158 |
| 73 | 146 | 146 | 247 | 255 | 235 | 154 | 130 |
| 97 | 166 | 117 | 231 | 243 | 210 | 117 | 117 |
| 117 | 190 | 36 | 146 | 178 | 93 | 20 | 170 |
| 130 | 202 | 73 | 20 | 12 | 53 | 85 | 194 |
| 146 | 206 | 130 | 117 | 85 | 166 | 182 | 215 |
Notice that the minimum value (52) is now 0 and the maximum value (154) is now 255.
Full-sized image[edit]
 |
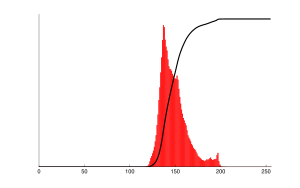 |
 |
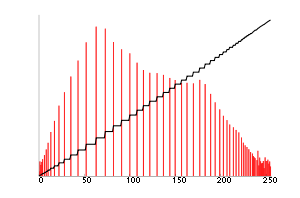 |
Advantages and Disadvantages[edit]
Advantages[edit]
- Better-Looking Images: Histogram equalization makes images look better by making the details clearer and improving their overall appearance.
- Helps Spot Things: It can help computer programs spot important features in images, which is handy for tasks like medical diagnosis or identifying objects.
- Easy to Use: You don't need to be an expert to use histogram equalization. It's straightforward and can be used by beginners in image editing and computer vision.
- Saves Time and Resources: Since it works directly on the image pixels, you don't need extra data or complicated setup, making it efficient for real-time applications and devices with limited computing power.
Disadvantages[edit]
- Can Make Things Look Strange: Sometimes, histogram equalization can make images look odd by exaggerating small details or making textures too prominent, which can be distracting.
- Not Good with Local Details: It might not preserve small details well, especially in areas of the image that have both bright and dark parts.
- Not Customizable Enough: It treats the whole image the same way, which might not work well for images with specific lighting conditions or unique characteristics.
- Tricky to Fine-Tune: Adjusting the settings for histogram equalization can be tricky, and getting it just right often requires a good understanding of image processing.
See also[edit]
- Histogram matching
- Adaptive histogram equalization
- Normalization (image processing)
- Digital image processing
- Image segmentation
See also[edit]
References[edit]
- ^ Hum, Yan Chai; Lai, Khin Wee; Mohamad Salim, Maheza Irna (October 11, 2014). "Multiobjectives bihistogram equalization for image contrast enhancement". Complexity. 20 (2): 22–36. Bibcode:2014Cmplx..20b..22H. doi:10.1002/cplx.21499.
- ^ Laughlin, S.B (1981). "A simple coding procedure enhances a neuron's information capacity". Z. Naturforsch. 9–10(36):910–2.
- ^ Intel Corporation (2001). "Open Source Computer Vision Library Reference Manual" (PDF). Retrieved January 11, 2015.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Gonzalez, Rafael C. (2018). Digital image processing. Richard E. Woods (4th ed.). New York, NY: Pearson. pp. 138–140. ISBN 978-1-292-22304-9. OCLC 991765590.
- ^ S. Naik and C. Murthy, "Hue-preserving color image enhancement without gamut problem," IEEE Trans. Image Processing, vol. 12, no. 12, pp. 1591–1598, Dec. 2003
- ^ P. E. Trahanias and A. N. Venetsanopoulos, "Color image enhancement through 3-D histogram equalization," in Proc. 15th IAPR Int. Conf. Pattern Recognition, vol. 1, pp. 545–548, Aug.-Sep. 1992.
- ^ N. Bassiou and C. Kotropoulos, "Color image histogram equalization by absolute discounting back-off," Computer Vision and Image Understanding, vol. 107, no. 1-2, pp.108-122, Jul.-Aug. 2007
- ^ Han, Ji-Hee; Yang, Sejung; Lee, Byung-Uk (2011). "A Novel 3-D Color Histogram Equalization Method with Uniform 1-D Gray Scale Histogram". IEEE Transactions on Image Processing. 20 (2): 506–512. Bibcode:2011ITIP...20..506H. doi:10.1109/TIP.2010.2068555. PMID 20801744. S2CID 17972519.
- Acharya and Ray, Image Processing: Principles and Applications, Wiley-Interscience 2005 ISBN 0-471-71998-6
- Russ, The Image Processing Handbook: Fourth Edition, CRC 2002 ISBN 0-8493-2532-3
- "Histogram Equalization" at Generation5 (archive)











![{\displaystyle [0,L-1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65750fadf4ccfc943115238508d7fdabfa887322)

















![{\displaystyle [0,255]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b92f49fdc420e36b9d62c711c3c6ebe7d9fcebc)