Independent equation

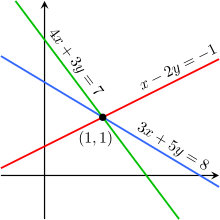
An independent equation is an equation in a system of simultaneous equations which cannot be derived algebraically from the other equations.^[1] The concept typically arises in the context of linear equations. If it is possible to duplicate one of the equations in a system by multiplying each of the other equations by some number (potentially a different number for each equation) and summing the resulting equations, then that equation is dependent on the others. But if this is not possible, then that equation is independent of the others.

If an equation is independent of the other equations in its system, then it provides information beyond that which is provided by the other equations. In contrast, if an equation is dependent on the others, then it provides no information not contained in the others collectively, and the equation can be dropped from the system without any information loss.^[2]

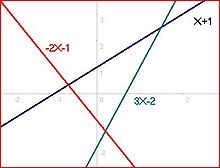
The number of independent equations in a system equals the rank of the augmented matrix of the system—the system's coefficient matrix with one additional column appended, that column being the column vector of constants.

The number of independent equations in a system of consistent equations (a system that has at least one solution) can never be greater than the number of unknowns. Equivalently, if a system has more independent equations than unknowns, it is inconsistent and has no solutions.

References

^ PSAT/NMSQT 2017 : strategies, practice & review with 2 practice tests. Kaplan Test Prep and Admissions, Kaplan Publishing (2017 ed.). New York. 2016. p. 38. ISBN 978-1-5062-1030-8. OCLC 953202269.{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: others (link)
^ Roe, E. D. (1918). "A Geometric Representation". The Mathematics Teacher. 10 (4): 205–210. doi:10.5951/MT.10.4.0205. ISSN 0025-5769. JSTOR 27950145.

This linear algebra-related article is a stub. You can help Wikipedia by expanding it.

[1] PSAT/NMSQT 2017 : strategies, practice & review with 2 practice tests. Kaplan Test Prep and Admissions, Kaplan Publishing (2017 ed.). New York. 2016. p. 38. ISBN 978-1-5062-1030-8. OCLC 953202269.{{cite book}}: CS1 maint: location missing publisher (link) CS1 maint: others (link)

[2] Roe, E. D. (1918). "A Geometric Representation". The Mathematics Teacher. 10 (4): 205–210. doi:10.5951/MT.10.4.0205. ISSN 0025-5769. JSTOR 27950145.

[1]

[2]

See also

References