Klein four-group
| Algebraic structure → Group theory Group theory |
|---|
 |
In mathematics, the Klein four-group is an abelian group with four elements, in which each element is self-inverse (composing it with itself produces the identity) and in which composing any two of the three non-identity elements produces the third one. It can be described as the symmetry group of a non-square rectangle (with the three non-identity elements being horizontal reflection, vertical reflection and 180-degree rotation), as the group of bitwise exclusive-or operations on two-bit binary values, or more abstractly as , the direct product of two copies of the cyclic group of order 2 by the Fundamental Theorem of Finitely Generated Abelian Groups. It was named Vierergruppe (German: [ˈfiːʁɐˌɡʁʊpə] ), meaning four-group) by Felix Klein in 1884.[1] It is also called the Klein group, and is often symbolized by the letter or as .
The Klein four-group, with four elements, is the smallest group that is not cyclic. Up to isomorphism, there is only one other group of order four: the cyclic group of order 4. Both groups are abelian.
Presentations
[edit]The Klein group's Cayley table is given by:
| * | e | a | b | c |
|---|---|---|---|---|
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
The Klein four-group is also defined by the group presentation
All non-identity elements of the Klein group have order 2, so any two non-identity elements can serve as generators in the above presentation. The Klein four-group is the smallest non-cyclic group. It is, however, an abelian group, and isomorphic to the dihedral group of order (cardinality) 4, symbolized (or , using the geometric convention); other than the group of order 2, it is the only dihedral group that is abelian.
The Klein four-group is also isomorphic to the direct sum , so that it can be represented as the pairs {(0,0), (0,1), (1,0), (1,1)} under component-wise addition modulo 2 (or equivalently the bit strings {00, 01, 10, 11} under bitwise XOR), with (0,0) being the group's identity element. The Klein four-group is thus an example of an elementary abelian 2-group, which is also called a Boolean group. The Klein four-group is thus also the group generated by the symmetric difference as the binary operation on the subsets of a powerset of a set with two elements—that is, over a field of sets with four elements, such as ; the empty set is the group's identity element in this case.
Another numerical construction of the Klein four-group is the set { 1, 3, 5, 7 }, with the operation being multiplication modulo 8. Here a is 3, b is 5, and c = ab is 3 × 5 = 15 ≡ 7 (mod 8).
The Klein four-group also has a representation as 2 × 2 real matrices with the operation being matrix multiplication:
On a Rubik's Cube, the "4 dots" pattern can be made in three ways, depending on the pair of faces that are left blank; these three positions together with the solved position form an example of the Klein group, with the solved position serving as the identity.
Geometry
[edit]
In two dimensions, the Klein four-group is the symmetry group of a rhombus and of rectangles that are not squares, the four elements being the identity, the vertical reflection, the horizontal reflection, and a 180° rotation.
In three dimensions, there are three different symmetry groups that are algebraically the Klein four-group:
- one with three perpendicular 2-fold rotation axes: the dihedral group
- one with a 2-fold rotation axis, and a perpendicular plane of reflection:
- one with a 2-fold rotation axis in a plane of reflection (and hence also in a perpendicular plane of reflection): .
Permutation representation
[edit]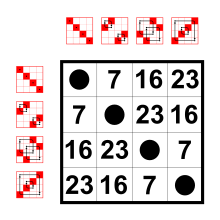

The three elements of order two in the Klein four-group are interchangeable: the automorphism group of V is thus the group of permutations of these three elements, that is, the symmetric group .
The Klein four-group's permutations of its own elements can be thought of abstractly as its permutation representation on four points:
- {(), (1,2)(3,4), (1,3)(2,4), (1,4)(2,3)}
In this representation, is a normal subgroup of the alternating group (and also the symmetric group ) on four letters. In fact, it is the kernel of a surjective group homomorphism from to .
Other representations within S4 are:
- { (), (1,2), (3,4), (1,2)(3,4) }
- { (), (1,3), (2,4), (1,3)(2,4) }
- { (), (1,4), (2,3), (1,4)(2,3) }
They are not normal subgroups of S4.
Algebra
[edit]According to Galois theory, the existence of the Klein four-group (and in particular, the permutation representation of it) explains the existence of the formula for calculating the roots of quartic equations in terms of radicals, as established by Lodovico Ferrari: the map corresponds to the resolvent cubic, in terms of Lagrange resolvents.
In the construction of finite rings, eight of the eleven rings with four elements have the Klein four-group as their additive substructure.
If denotes the multiplicative group of non-zero reals and the multiplicative group of positive reals, then is the group of units of the ring , and is a subgroup of (in fact it is the component of the identity of ). The quotient group is isomorphic to the Klein four-group. In a similar fashion, the group of units of the split-complex number ring, when divided by its identity component, also results in the Klein four-group.
Graph theory
[edit]Among the simple connected graph, the simplest (in the sense of having the fewest entities) that admits the Klein four-group as its automorphism group is the diamond graph shown below. It is also the automorphism group of some other graphs that are simpler in the sense of having fewer entities. These include the graph with four vertices and one edge, which remains simple but loses connectivity, and the graph with two vertices connected to each other by two edges, which remains connected but loses simplicity.
Music
[edit]In music composition, the four-group is the basic group of permutations in the twelve-tone technique. In that instance, the Cayley table is written[2]
| S | I | R | RI |
|---|---|---|---|
| I | S | RI | R |
| R | RI | S | I |
| RI | R | I | S |
See also
[edit]References
[edit]- ^ Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade (Lectures on the icosahedron and the solution of equations of the fifth degree)
- ^ Babbitt, Milton. (1960) "Twelve-Tone Invariants as Compositional Determinants", Musical Quarterly 46(2):253 Special Issue: Problems of Modern Music: The Princeton Seminar in Advanced Musical Studies (April): 246–59, Oxford University Press
Further reading
[edit]- M. A. Armstrong (1988) Groups and Symmetry, Springer Verlag, page 53.
- W. E. Barnes (1963) Introduction to Abstract Algebra, D.C. Heath & Co., page 20.



























