Lemniscate of Gerono

The lemniscate of Gerono

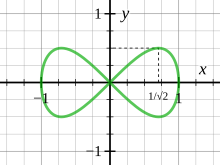
In algebraic geometry, the lemniscate of Gerono, or lemnicate of Huygens, or figure-eight curve, is a plane algebraic curve of degree four and genus zero shaped like an $\infty$ symbol, or figure eight. It has equation

x⁴ − x² + y² = 0.

It was studied by Camille-Christophe Gerono.

Because the curve is of genus zero, it can be parametrized by rational functions; one means of doing that is

$x = \frac{t^2-1}{t^2+1},\ y = \frac{2t(t^2-1)}{(t^2+1)^2}.$

Another representation is

$x = \cos \varphi,\ y = \sin\varphi\,\cos\varphi = \sin(2\varphi)/2$

which reveals that this lemniscate is a special case of a lissajous figure.

The dual curve (see Plücker formula), pictured below, has therefore a somewhat different character. Its equation is

(x² − y²)³ + 8y⁴ + 20x²y² − x⁴ − 16y² = 0.

Dual to the lemniscate of Gerono

References

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 124. ISBN 0-486-60288-5.