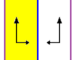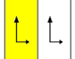List of planar symmetry groups
This article summarizes the classes of discrete symmetry groups of the Euclidean plane. The symmetry groups are named here by three naming schemes: International notation, orbifold notation, and Coxeter notation. There are three kinds of symmetry groups of the plane:
- 2 families of rosette groups – 2D point groups
- 7 frieze groups – 2D line groups
- 17 wallpaper groups – 2D space groups.
Rosette groups[edit]
There are two families of discrete two-dimensional point groups, and they are specified with parameter n, which is the order of the group of the rotations in the group.
| Family | Intl (orbifold) |
Schön. | Geo [1] Coxeter |
Order | Examples | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cyclic symmetry | n (n•) |
Cn | n [n]+ |
n |  C1, [ ]+ (•) |
 C2, [2]+ (2•) |
 C3, [3]+ (3•) |
 C4, [4]+ (4•) |
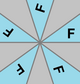 C5, [5]+ (5•) |
 C6, [6]+ (6•) |
| Dihedral symmetry | nm (*n•) |
Dn | n [n] |
2n |  D1, [ ] (*•) |
 D2, [2] (*2•) |
 D3, [3] (*3•) |
 D4, [4] (*4•) |
 D5, [5] (*5•) |
 D6, [6] (*6•) |
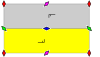
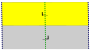
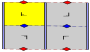
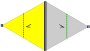
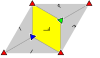
Frieze groups[edit]
The 7 frieze groups, the two-dimensional line groups, with a direction of periodicity are given with five notational names. The Schönflies notation is given as infinite limits of 7 dihedral groups. The yellow regions represent the infinite fundamental domain in each.
|
|
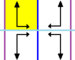
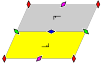
Wallpaper groups[edit]
The 17 wallpaper groups, with finite fundamental domains, are given by International notation, orbifold notation, and Coxeter notation, classified by the 5 Bravais lattices in the plane: square, oblique (parallelogrammatic), hexagonal (equilateral triangular), rectangular (centered rhombic), and rhombic (centered rectangular).
The p1 and p2 groups, with no reflectional symmetry, are repeated in all classes. The related pure reflectional Coxeter group are given with all classes except oblique.
|
|
|
|
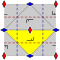
Wallpaper subgroup relationships[edit]
| o | 2222 | ×× | ** | *× | 22× | 22* | *2222 | 2*22 | 442 | 4*2 | *442 | 333 | *333 | 3*3 | 632 | *632 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p1 | p2 | pg | pm | cm | pgg | pmg | pmm | cmm | p4 | p4g | p4m | p3 | p3m1 | p31m | p6 | p6m | ||
| o | p1 | 2 | ||||||||||||||||
| 2222 | p2 | 2 | 2 | 2 | ||||||||||||||
| ×× | pg | 2 | 2 | |||||||||||||||
| ** | pm | 2 | 2 | 2 | 2 | |||||||||||||
| *× | cm | 2 | 2 | 2 | 3 | |||||||||||||
| 22× | pgg | 4 | 2 | 2 | 3 | |||||||||||||
| 22* | pmg | 4 | 2 | 2 | 2 | 4 | 2 | 3 | ||||||||||
| *2222 | pmm | 4 | 2 | 4 | 2 | 4 | 4 | 2 | 2 | 2 | ||||||||
| 2*22 | cmm | 4 | 2 | 4 | 4 | 2 | 2 | 2 | 2 | 4 | ||||||||
| 442 | p4 | 4 | 2 | 2 | ||||||||||||||
| 4*2 | p4g | 8 | 4 | 4 | 8 | 4 | 2 | 4 | 4 | 2 | 2 | 9 | ||||||
| *442 | p4m | 8 | 4 | 8 | 4 | 4 | 4 | 4 | 2 | 2 | 2 | 2 | 2 | |||||
| 333 | p3 | 3 | 3 | |||||||||||||||
| *333 | p3m1 | 6 | 6 | 6 | 3 | 2 | 4 | 3 | ||||||||||
| 3*3 | p31m | 6 | 6 | 6 | 3 | 2 | 3 | 4 | ||||||||||
| 632 | p6 | 6 | 3 | 2 | 4 | |||||||||||||
| *632 | p6m | 12 | 6 | 12 | 12 | 6 | 6 | 6 | 6 | 3 | 4 | 2 | 2 | 2 | 3 |
See also[edit]
- List of spherical symmetry groups
- Orbifold notation#Hyperbolic plane - Hyperbolic symmetry groups
Notes[edit]
- ^ The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF [1]
- ^ Coxeter, (1980), The 17 plane groups, Table 4
References[edit]
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5 (Orbifold notation for polyhedra, Euclidean and hyperbolic tilings)
- On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- Coxeter, H. S. M. & Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.
- N. W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 12: Euclidean Symmetry Groups
External links[edit]
- "Conway's manuscript" on Orbifold notation (Notation changed from this original, x is now used in place of open-dot, and o is used in place of the closed dot)
- The 17 Wallpaper Groups